中国城市经济增长的收敛性研究

崔俊富 陈金伟 苗建军

1（南京航空航天大学经济与管理学院，南京 211106）

2（南京审计大学经济学院，南京 211815）

引 言

自有人类文明以来，经济增长就是人类发展的核心问题之一。从历史数据来看，人类经济曾长期处于低水平增长阶段，几百万年的人类发展史更多的是解决 “吃饭”问题，这一现象直到工业革命之后才得以改观。纵观人类发展史，特别是近期工业革命之后的各个国家、地区的经济增长情况，许多成果都力图回答经济增长的源泉是什么？为什么有些国家、地区的经济增长速度较快，而有些国家、地区的经济增速较慢？是什么原因导致部分国家、地区经济达到中等收入阶段之后增速下滑，进入了所谓的 “中等收入陷阱”阶段，这些国家、地区最终能走出 “中等收入陷阱”吗？[1]

Solow（1956； 1957）[2，3]构建了包含产出、资本、劳动、知识4个变量的经济增长模型，对美国经济增长情况进行了研究，发现资本、劳动对经济增长起到了非常重要的作用，但是都没有知识起到的作用大，知识贡献了87.5%的人均产出增长。Arrow（1962）[4]发现在飞机制造中，即使生产过程没有明显革新，飞机生产时间与飞机生产数量的立方根存在反比例关系，于是他认为知识的产生来源于经验的积累，也就是 “干中学”（Learning by Doing）或 “边投资边学”（Learning by Investing）。 Lucas（1988）[5]关注人力资本在经济增长中的重要作用，认为人力资本对经济增长具有显著的正效应，人力资本生产可以放松资本的边际报酬递减约束，对技术进步形成一定程度的替代，从而促进人均产出的长期增长。其他学者在上述学者的基础上进行了一定程度的扩展，也得出了一些有益结论。整体来看，现有成果对经济增长源泉的回答可以归结为资本、人口、技术进步、制度变革等。

目前世界各个国家、地区经济增长状况存在极大的差异，表1显示了世界GDP在100亿美元以上的国家、地区的GDP、人均GDP和GDP增长率指标情况。从GDP指标来看，平均值为5882.2亿美元，标准差为22139.0亿美元，最大值为208937.5亿美元，最小值仅100.4亿美元，最大值是最小值的2000多倍，最大值在9个标准差之外。从人均GDP指标来看，平均值为15198.7美元，标准差为19125.4美元，最大值为82080美元，最小值仅320美元，最大值是最小值的256.5倍，最大值在3个标准差之外。从GDP增长率来看，平均值为2.6%，标准差为4.4%，最大值为13.4%，最小值仅-34.3%，最大值比最小值高47.7个百分点，最大值在2个标准差之外。设想一种极端的情况，假如经济总量最大的国家、地区保持经济不增长，而经济总量最低的国家、地区保持一定的增长速度来追赶，每年10%的高速增长需要81年，每年5%的中速增长需要157年，每年2%的低速增长需要386年；假如人均GDP最高的国家、地区保持不变，而人均GDP最低的国家、地区保持一定的增长速度来追赶，每年10%的高速增长需要59年，每年5%的中速增长需要114年，每年2%的低速增长需要281年。结论似乎很悲观，这也证明了研究经济增长的深刻意义[6]。

表1 世界部分国家、地区经济指标情况

从发展过程来看，部分发展中国家、地区追赶发达国家、地区受困于 “中等收入陷阱”。该现象指的是中等收入经济体在迈向高收入阶段时，经济出现停滞和反复，人均国民收入无法突破中等收入水平，达到高等收入水平。马来西亚、泰国、印度尼西亚、菲律宾等东南亚国家，哥伦比亚、墨西哥等美洲国家都不同程度地陷入了 “中等收入陷阱”。这些国家之所以会陷入 “中等收入陷阱”，主要是因为产业升级困难、科技创新不足、政治社会动荡、社会福利失衡等原因，跨越 “中等收入陷阱”必须解决这些问题[1]。

1 经济增长收敛性与检验

收敛性是经济增长理论的重要结论之一，对经济增长收敛性的讨论有利于深化经济增长相关问题的研究，可以帮助回答经济增长的源泉、经济增长的速度差异、跨越 “中等收入陷阱”等问题。

1.1 经济增长收敛性的内涵

经济增长收敛性的讨论来源于Solow（1956；1957）[2，3]的开拓性贡献。 Ramsey（1928）[7]、Dimond（1965）[8]、Romer（1990）[9]、Aghion 和 Howitt（1992）[10]、Jones（2002）[11]构建的经济增长模型也可以得出类似的结论。经济增长趋于收敛似乎是显而易见的，人均GDP越高，经济增速越低是人们的直观感觉，也符合自然规律。但是，理论上的探讨与经济运行实践不一定完全一致，Baumol（1986）[12]研究了16个工业国家的经济增长情况，认为收敛性存在，DeLong（1988）[13]却证明 Baumol（1986）的结论不准确，收敛性并不存在。那么中国内部区域的经济增长符合这一规律吗？目前也未达成统一的认识。周国富和夏实谦（2008）[14]认为黄河流域九省区存在显著的条件收敛。朱国忠等（2014）[15]研究了中国省级区域经济增长收敛性情况，发现中国省级区域经济增长总体上不存在收敛性，落后省区的增长速度并不比富裕省区的增长速度高。周少甫和陈哲（2020）[16]研究发现，全国和三大地区的经济增长是收敛的，人口流动对各地区的经济增长均呈现负效应。

综合各研究成果，经济增长收敛性指的是随着时间的持续推进，各经济体的经济增速趋于一个恒定的值，这也就意味着人均GDP与经济增速是负相关关系。经济增长各理论模型得出的结论是相似的，为了简化分析，本文选择采用Solow模型分析框架来进行研究。

1.2 Solow模型对经济增长收敛性的讨论

Solow模型假定生产函数为柯布道格拉斯形式，且边际报酬递减：

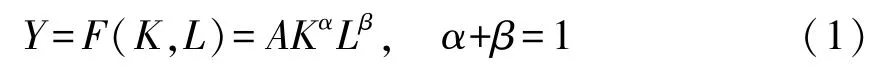
资本存量变化与投资和折旧紧密相关：

其中投资为总产出的固定比例：

联立式（1）～（3）可得：

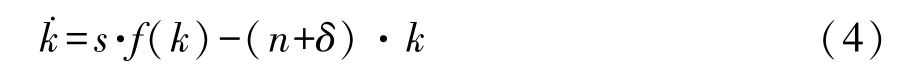
在柯布道格拉斯生产函数形势下，y＝kα，于是：

也就是经济增长的收敛性表现为经济增速收敛于人口增长率和科技进步之和gL+gA。

1.3 经济增长收敛性的检验

Solow模型研究的经济增长收敛性是函数最优化探讨，模型构成变量都是连续型的，而现实中的经济增长数据却是离散的，必须借助数理统计方法来检验经济增长收敛性[17]。由式（4）可知：

也就是，资本存量k与经济增长速度是负相关关系，不同经济体相互比较，资本存量k越大经济增速越低，资本存量k越小经济增速越高。资本存量k和人均GDP紧密相关，因此可以通过测算经济增速与人均GDP的线性相关系数是否小于零来检验是否存在收敛性[18]，即：

其中，xi和yi分别代表i地区的GDP速度和人均GDP，如果线性相关系数ρ为负值，说明随着人均GDP由高到低，经济增速也越来越快，也就是经济增长是收敛的。

2 中国城市经济增长收敛性的检验矛盾

城市是人类文明的聚集。改革开放以来，中国经济迅速增长，目前经济总量已稳居世界第2位，人均GDP也突破1万美元。在中国经济发展过程中，城市经济的持续发展壮大提供了有力支撑作用，尤其是深圳等新兴城市短短几十年就从一个小渔村发展成国际性大都市。2019年北京、上海、深圳3个城市地区生产总值占全国GDP的比重达到10.1%，地方一般公共预算收入占全国一般公共预算收入的比重达到8.8%。因此，准确把握中国城市的经济增长特征对于中国经济的平稳较快增长具有非常重要的现实意义。那么中国城市经济增长是否符合收敛性特征呢？

根据代表性、科学性、可获得性的原则，考虑中国不同区域的不同发展特点，本文选择北京、上海、重庆、广州、深圳、哈尔滨、南京、杭州、郑州、武汉、长沙、成都、南宁、兰州、宁波、青岛16个城市作为研究对象。数据来源于 《中国统计年鉴》、《中国城市统计年鉴》及各城市统计年鉴，数据范围为1985～2019年。经济增速和人均GDP对数的排序如表2所示，经济增速和人均GDP对数散点图如图1所示。可以发现，收敛性基本不存在，城市人均GDP对数与经济增速更有可能是正线性关系，人均GDP对数越高的城市，如杭州、深圳、北京等的经济增速相对也越高，人均GDP对数越低的城市，如南宁、兰州、哈尔滨等的经济增速相对也越低。

图1 城市经济增速与人均GDP对数散点图

表2 城市经济增速、人均GDP对数排序情况

测算经济增速与人均GDP对数的线性相关系数，可以发现，经济增速与人均GDP对数的负线性相关关系基本不存在，线性相关系数为0.29，但是未通过显著性检验，P值高达0.28，也就是中国城市经济增长不存在收敛性。这就出现了矛盾：（1）与直观感觉相矛盾，直观上人均GDP越高，说明经济运行成本越高，经济存量越大，经济增速越低，反之人均GDP越低，说明经济运行成本越低，经济存量越小，经济增速越高；（2）与经济理论相矛盾，Solow模型等经济学模型说明不同经济体的经济增速存在收敛性。

表3 城市经济增速与人均GDP对数线性相关性

需要指出的是，“存在即合理”虽然有些太过于绝对，但是，任何矛盾的解释都必须基于现实经济实践是合理的这一基础。直观感觉和经济理论可能是不合理的，而现实经济实践一定是合理的，如果直观感觉和经济理论无法解释现实经济实践，那么说明直观感觉和经济理论必须修正，甚至完全推翻。

3 中国城市经济增长收敛性的再讨论

解释中国城市经济增长实践与直观感觉、经济理论的矛盾必须探讨中国城市经济增长的动力。由Solow模型表达式可知，生产函数包括产出、资本、人力、科技进步4个变量，产出决定于资本、人力、科技进步的贡献。

3.1 中国城市经济增长的动力

3.1.1 基于面板数据模型的中国城市经济增长动力讨论

受到数据的限制，无法建立产出、资本、人力、科技进步4个变量的经济增长模型，先建立面板数据模型研究经济增长与资本、人口的关系。面板数据模型比经典的线性回归模型能反映出更多的信息，截面数据模型或时间序列数据模型只能反映两维信息，而面板数据模型可以从三维角度研究变量之间的关系[19]。面板数据模型的一般形式为：

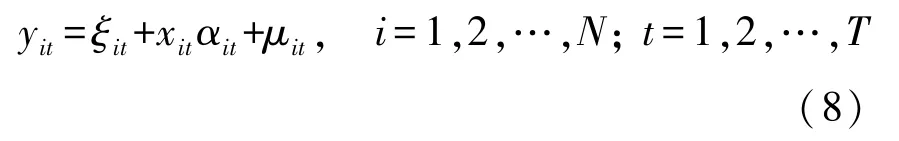
模型常数项为参数ξit，解释变量xit的系数为αit，截面成员个数为N，每个截面成员的观测时期总数为T。根据个体影响、结构变化的表现形式可以分为不变系数、变截距和变系数模型：

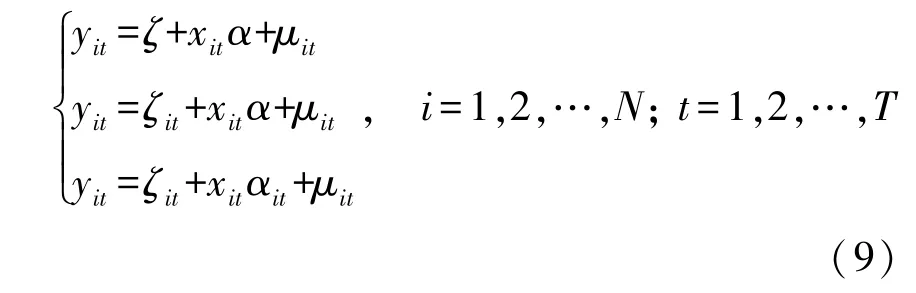
本文使用考虑个体影响的变截距模型来研究中国城市经济增长的动力情况，建立模型：

其中，GDPit为地区生产总值，表示经济产出；Kit为固定资产投资，衡量资本影响；Lit为人口，衡量人力影响。α和β为回归系数，分别表示资本和人口的影响程度，当α和β为正值时，说明因变量和自变量是正相关关系，随着资本、人口的投入量增加，经济产出增加；当α和β为负值时，说明因变量和自变量是负相关关系，随着资本、人口的投入量增加，经济产出减少。由于是对数形式，因此回归系数α和β分别表示经济产出对于投入变量资本和人口的弹性，分别是资本产出弹性和人口产出弹性。模拟结果如下：

注：∗∗∗、∗∗、∗分别表示通过0.01、0.05、0.1的显著性水平检验。

模型拟合结果是优良的，可决系数达到了0.97，说明自变量可以解释大部分因变量，所有的变量都通过了显著性水平为0.01的显著性检验。对数形式固定资产投资和人口的系数分别为0.73和0.83，说明地区生产总值对固定资产投资和人口的弹性分别为0.73和0.83，也就是固定资产和人口增长1个百分点，地区生产总值分别增长0.73和0.83个百分点，这说明资本和人力对中国城市经济增长都很重要，人力更加重要。

3.1.2 基于数据包络分析的全要素生产率测度

整体来看，可决系数较高，参数通过显著性检验，说明尽管Solow模型简单，仍然对中国城市经济增长具有非常强的解释力。不过，这里存在一个问题，科技进步A没有得到反映。在Solow模型中，一般用模型无法解释的部分来反映科技进步A，这部分被称为Solow余值。Solow余值概念简单，计算快捷，具有非常广泛的应用，但是Solow余值测算精度不高，过于粗糙。为了克服Solow余值的缺点，本文使用基于数据包络分析的Malmquist指数测算全要素生产率来反映科技进步[20，21]。 瑞典统计学家 Malmquist（1953）[22]研究消费时提出了 Malmquist指数，Färe 等（1994）[23]基于数据包络分析方法，将Malmquist指数进行了分解。 Ray和 Desli（1997）[24]对分解方法进行了修正，确定为如下形式：

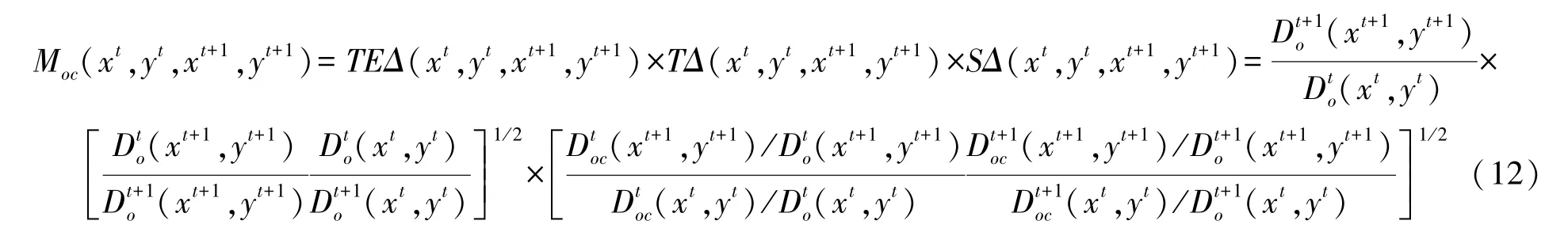
Malmquist指数分解式中，TEΔ（xt，yt，xt+1，yt+1）反映纯技术效率变化，TΔ（xt，yt，xt+1，yt+1）反映技术水平变化，SΔ（xt，yt，xt+1，yt+1）反映规模效率变化[25]。Malmquist指数反映的科技进步排序结果在表4中显示，南京、北京、深圳等城市排序较高，哈尔滨、长沙、南宁等城市排序较低。

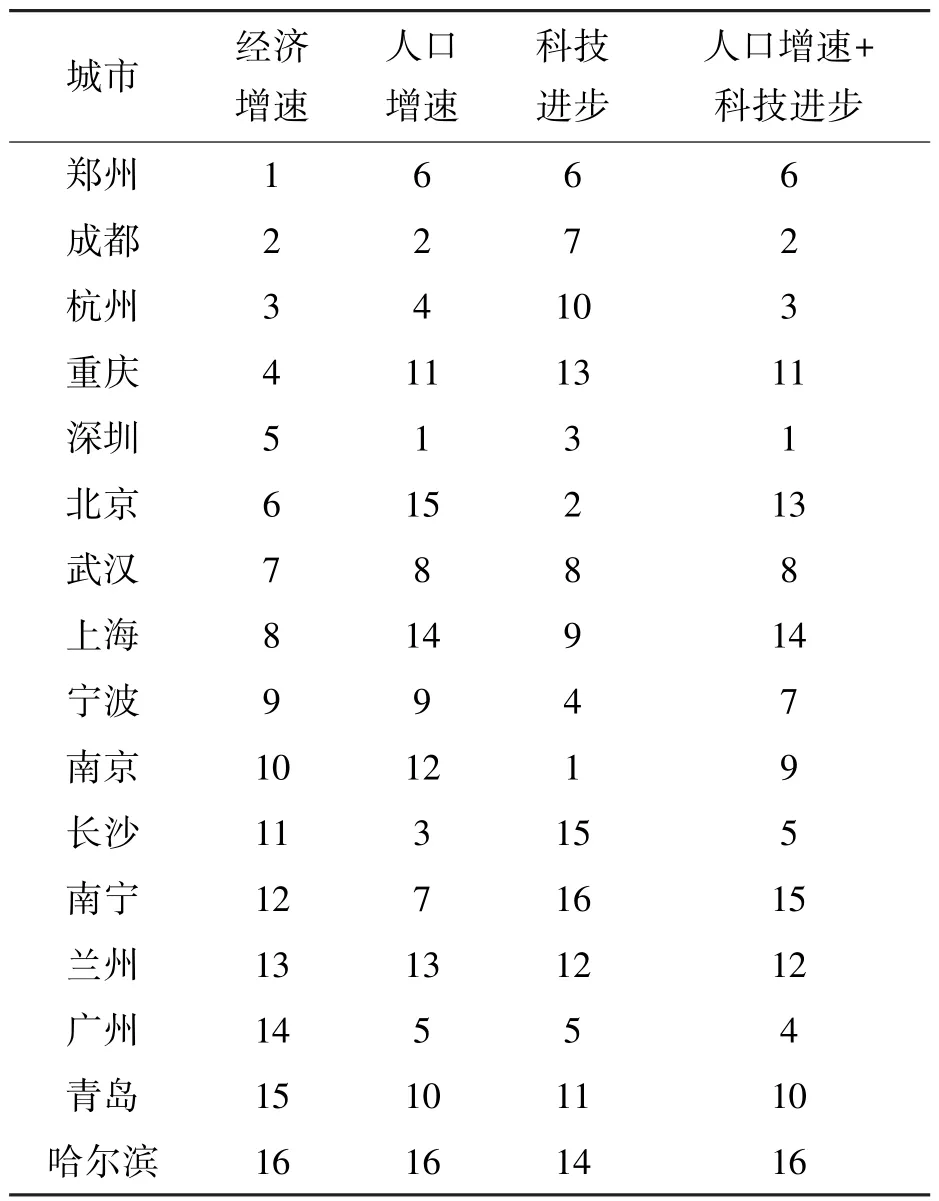
表4 城市经济增速、人口增速、科技进步、人口增速+科技进步排序情况

3.2 中国城市经济增长与人口增速、科技进步的线性关系

式（5）表明，经济增长满足收敛性的一个重要结论是经济增速与人口增速、科技进步之和呈现线性关系，将经济增速、人口增速、科技进步3个变量的排序情况汇总到表4。可以发现，经济增速与人口增速较大可能是正线性相关关系，人口增速较高的城市如郑州、成都、杭州的经济增速也较高，人口增速较低的城市如兰州、青岛、哈尔滨的经济增速也较低。经济增速与科技进步可能也是正线性相关关系，科技进步较高的城市，如深圳、北京的经济增速也较高，科技进步较低的城市，如青岛、哈尔滨的经济增速也较低。

测算Pearson线性相关系数，经济增速与人口增速的Pearson线性相关系数为0.47，通过了显著性水平为0.1的显著性检验，经济增速与科技进步的Pearson线性相关系数为0.38，未通过显著性水平为0.1的显著性检验。整体来看，虽然经济增长与科技进步的Pearson线性相关系数未通过显著性检验，但是P值也不高，仅为0.15，可以基本判断经济增速与人口增速、科技进步都呈现正线性相关性，也就是人口增速、科技进步越高，经济增速也越高[26]。

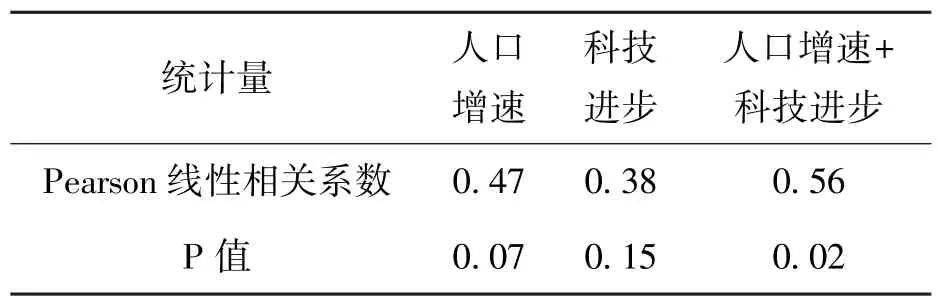
表5 城市经济增速与人口增速、科技进步、人口增速+科技进步的线性相关性

式（5）描述的是经济增速等于人口增速、科技进步之和，因此，研究经济增速与人口增速、科技进步之和的线性关系更有意义。构建新变量人口增速+科技进步并进行排序，结果如表4所示，绘出散点图如图2所示。可以发现，经济增速与新变量人口增速+科技进步大概率是正线性相关关系，人口增速+科技进步越高的城市，如郑州、成都、杭州的经济增速也越高，人口增速+科技进步越低的城市，如青岛、哈尔滨的经济增速也越低。测算Pearson线性相关系数，经济增速与人口增速+科技进步的Pearson线性相关系数高达0.56，通过了显著性水平为0.05的显著性检验。这里需要特别指出的是，Solow模型研究的经济增长收敛性是函数最优化探讨，结果是比较完美的，而计量分析、全要素生产率测算使用的是离散数据，不太可能获得数理模型的完美结果。Pearson线性相关系数高达0.56，且P值仅为0.02，已经有足够的依据相信式（5）是成立的，研究结论有较高的说服力，只是经济增速与人口增速、科技进步之和的线性关系系数不是1，而是0.56。

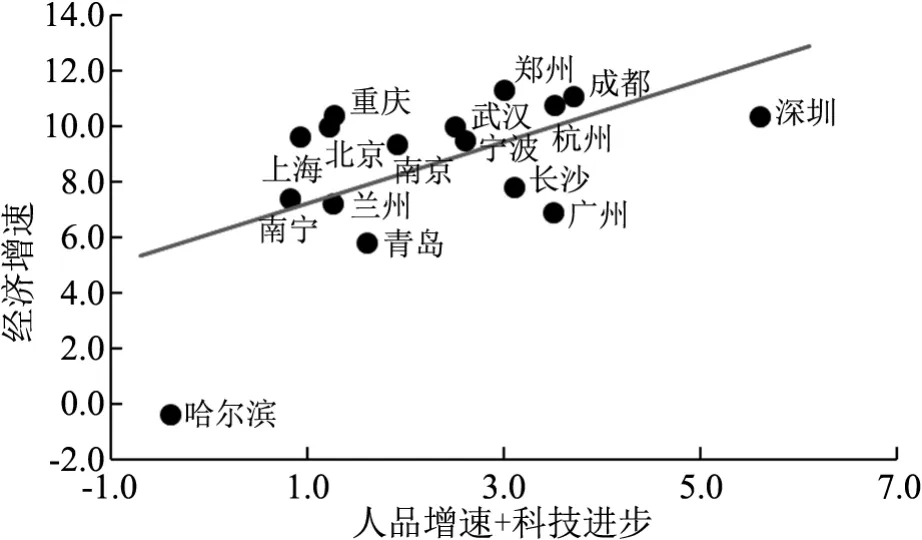
图2 城市经济增速与人口增速+科技进步散点图

中国城市经济增速与人口增速+科技进步呈现比较明显的正线性相关关系，说明中国城市经济增长与经济理论是相符的，经济实践与经济理论的矛盾是不存在的，也就是中国城市经济增长存在收敛性，只是由于生产要素的不同导致经济增速出现了较大差异，进而影响了人们的直观感觉。深圳等城市的经济之所以高速增长，主要是因为人口增长、科技进步较快，而青岛、哈尔滨等城市人口增长、科技进步较慢从而经济增速趋缓。

4 结 语

经济增长收敛似乎是显而易见的，符合人们的直观感觉，也是经济增长理论的重要结论之一。Pearson线性相关系数显示中国城市经济增长收敛性基本不存在，经济增速与城市人均GDP更有可能是正线性关系，人均GDP越高的城市经济增速相对也越高，这与直观感觉、经济理论相矛盾。基于面板数据模型可知Solow模型对中国城市的经济增长具有非常高的解释力。深入讨论中国城市经济增长与人口增速、科技进步的线性关系，发现中国城市经济增速与人口增速、科技进步之和呈现比较明显的正相关关系，说明中国城市经济增长与经济理论是相符的，也就是中国城市经济增长存在收敛性，只是由于生产要素的不同导致经济增速出现了较大差异，进而影响了人们的直观感觉。从保持经济长期平稳发展的角度，中国各城市应当加强资本、人力、科技进步、制度创新等要素的积累与提升。

（1）加大物质资本积累。物质资本是经济增长理论关注的核心要素之一，Solow模型和Ramsey模型都是以物资资本作为切入点来对经济增长进行讨论，认为经济发展水平决定于物资资本积累情况。改革开放以来，中国城市经济迅速发展与物资资本积累紧密相关。改革开放初期，物资资本比较匮乏，通过国家投资和引进外资，提高了物资资本积累水平，促进了经济增长。当前我国城市经济，特别是工业等资本密集型产业的物资资本积累已经不像改革开放初期那样匮乏，但是也必须注意，未来中国城市的发展仍然必须以物资资本积累作为基础，尤其是新材料、新能源等战略性新兴产业离不开物资资本的大量积累。应该充分调动民间资本的积极性和创造性，引导其进入实体经济，同时充分发挥政府资本的关键作用，支持重点行业的发展。

（2）提高人力资本积累。人力资本是城市经济腾飞的必要条件，丰富的劳动力资源保证了改革开放初期初层次加工业的迅速发展。未来将大力发展的高水平制造业、现代服务业同样必须依赖于充足的人力资本储备。当前，我国已经进入老龄化社会，发达国家的老龄化过程长达几百年，而且是在工业化完成之后才进入老龄化社会。我国的老龄化过程时间较短，尤其是工业化、信息化尚未完成，城市人力资本储备面临巨大的压力。可以进一步调整生育政策，适当鼓励人口生育，增加人口供给，逐步完善优化人口结构；还可以大力发展教育事业、卫生事业和文化事业，提高劳动力知识水平、身体素质和文化素养，建设一支优质劳动力队伍。

（3）促进科技进步。科技是第一生产力，在所有的生产要素中，科技要素是最有活力的生产要素。改革开放以来，中国各城市不断提高科技投入水平，科技进步迅速，有力地推动了经济增长。目前新一轮科技革命方兴未艾，科技发展日新月异，新的科学发现不断涌现。技术创新深刻地影响了世界发展，重塑了经济版图，新产业、新业态层出不穷。各城市必须牢牢抓住科技革命带来的新机遇，把科技创新摆在发展全局的核心位置，优化科技创新环境，完善科技创新政策，在生物医药、新能源、新材料等重大领域加大投入，持续增强科技创新贡献力。

（4）推进制度创新。制度领域的持续创新释放了经济发展的巨大潜力，保证了近期中国城市经济的迅速发展。锐意推动改革，使市场在资源配置中发挥基础作用，消除影响生产力发展的障碍藩篱，发现价格、优化供需；不断扩大开放，来料加工、来料装配、来样加工和补偿贸易迅速壮大了制造业，外部资源的利用也带来了先进的技术和管理理念，促进中国城市本土企业的快速成长。目前中国城市各方面成本逐步上升，资源比较优势正在下降，加之世界保护主义越发严重，面临的外部环境不确定性正在加大。必须持续推进制度创新，继续全面深化改革，摈弃不符合发展大势的思想观念，清除体制机制弊端，增强生产力发展的动力；继续扩大对外开放，推进 “丝绸之路经济带”和 “21世纪海上丝绸之路”建设，加强与其他国家、地区的密切联系，形成多方共赢、互动发展的良好局面。