信息差分遗传算法反算路面结构模量

鲁云岗,李跃军

(1.湖南省高速公路集团有限公司，湖南 长沙 410011;2.湖南省交通科学研究院有限公司，湖南 长沙 410015)

落锤式弯沉仪(FWD：Falling Weight Deflectometer)克服了传统贝克曼梁的诸多缺点，并且其结果与贝克曼梁具有良好的相关性，国内外对基于FWD实测弯沉盆的路面模量反算问题开展了大量研究[1-4]。模量反算是通过选取恰当的最优化算法和数据处理方法，使得计算弯沉盆尽可能好地拟合实测弯沉盆。由于理论弯沉计算的高度非线性，故路面模量反算是一个复杂的非线性最优化问题，没有理论上的精确解析解。

早期研究人员主要通过研究弯沉盆参数与路面各层模量或应力应变之间的关系，得到回归公式或者诺模图，来研究各因素对模量反算结果的影响。这种称之为回归公式法或图标法，它具有快速、简便等优势，很容易推广利用，但计算结果需要修正，精度不高，通用性差。

基于理论分析模型计算弯沉盆迭代法便于编程，可以综合不同理论分析模型优势，具有良好的扩展性。但它易受初值、迭代方法和确定修正值过程中可能产生病态矩阵等影响，导致收敛于局部最优。

数据库搜索法属经验法[5]，以美国的MODULUS反算程序最为著名。但对不同的路面结构需构建不同的数据库，否则将存在通用较差、有时误差较大的问题。

利用人工神经网络(ANN，Article Neutral Network)的高度非线性映射能力，MEIER[6]等将其引入路面模量反算领域，取得了一系列的成功。查旭东[7]研究了同伦神经网络在模量反算中的应用。但神经网络反算模量的精度受网络结构、规模、训练样本等因素影响，一般误差较大。

遗传算法是一种随机、自适应启发式搜索算法，对不同非线性问题具有鲁棒性，结果满足全局最优性。TSAI[8]等对遗传算法在路面反算领域应用进行了较为深入研究。本文作者曾采用自适应信息素对遗传算法进行了改进，能在不降低反算结果精度前提条件下大大提高模量反算求解效率[9]。由于遗传算法种群多样性很大程度上由变异概率决定，这影响到了算法全局收敛性。但算法对变异概率非常敏感，稍大的变异概率将迅速降低算法效率。

与遗传算法传统单一的父代染色体交叉不同的是，差分进化算法的每个子代生成过程中均可用到多个个体的线性组合，这丰富了子代个体的多样性[10]。因此，本文考虑将差分进化算法融入自适应信息遗传算法中，以此提高算法的全局收敛性。同时，考虑到FWD系统中存在传感器读数误差，对其进行了简单有效的权值处理。与单一的差分进化算法和自适应信息遗传算法相比，新算法能够在解空间中搜索到更为有效的最优解。

1 新算法的提出

新算法以自适应信息遗传算法为基本框架来组织，融合了差分、进化过程。算法基本步骤如图 1所示。

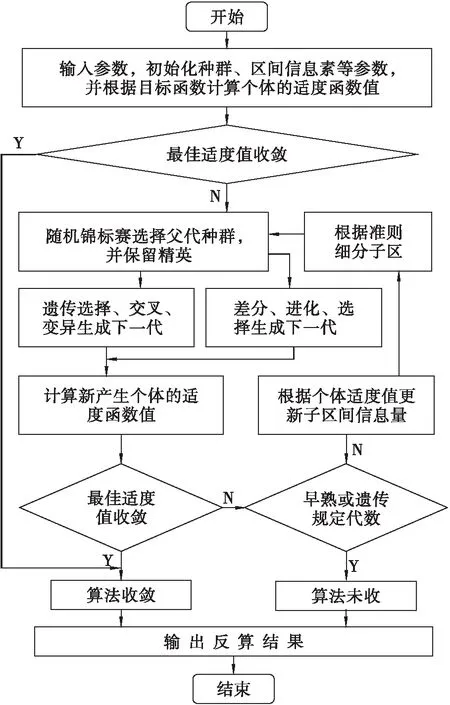
图1 差分信息遗传算法基本过程

1.1 确定目标函数

遗传算法遵循大自然优胜劣汰的生存法则，适应值越大越能存活，越是优秀的基因越能保存下来。模量反算的目标是使得相对误差的平方和最小，为此提出如下带权的约束优化数学模型式(1)来描述模量反算问题：

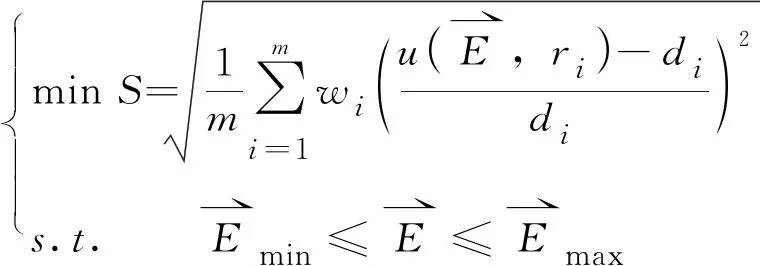
(1)

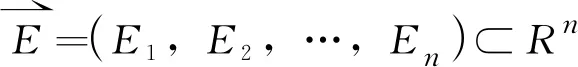
a.尽管FWD中系统误差可通过校正去除，但随机误差无法避免。由于测量误差的存在，不可能每个传感器具有同样的权重。

b.弯沉盆中越靠近落锤中心传感器读数越大，即相对误差越小。从消除误差影响来看，相对误差越小的传感器占的权重应该越大。

c.选择wi=di作为权既能反映前面2条，计算又相当简单。

1.2 染色初始化

从模量反算结果精度考虑，选择使用实数编码，一个染色体即为一组模量。将基因(模量)定义域均匀细分形成细分空间，然后再细分空间中产生随机均匀初始种群。根据落在每个维度子区间个体适度函数值，即可计算该子区间信息量[9]。

1.3 选择父代

选择当前种群中个体适应度高的优良个体，作为下一代种群的父代。这里选择带区间信息素选择概率公式作为适度函数值选择的标准，通过改进锦标赛准则选择父代种群，同时保留精英个体[9]。

1.4 遗传操作

使用交叉算子串并行组合来对父代个体进行交叉操作。至于变异算子，在算法初期采用噪声扰动式的蠕动变异算子，当反算结果有早熟迹象时，辅助使用定义域范围内突变算子。

1.5 差分进化

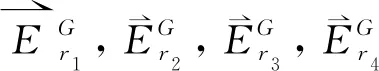
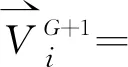
(2)

若生成的子代个体第k个基因超出给定范围时，则使用以下算子进行修正：

超出下界时：

(3)

超出上界时：

(4)

其中，rand为[0，1]上的随机数；

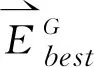
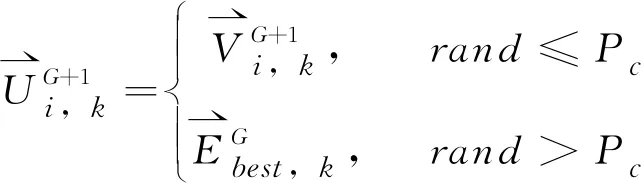
(5)

这步操作完后，将遗传操作和差分进化操作产生的子代种群合并，然后计算它们的个体适度函数值。若最佳适度函数值收敛则输出收敛结果；若早熟或达到最大遗传规定代数，则输出未收敛结果；否则进入下一步操作。

1.6 子区间操作

对每个子区间，根据落在子区间上个体的适度函数值更新该子区间的信息素[9]。

2 理论结果分析

表1为作者自主开发的反算程序PDGA(Pheromone Differential Genetic Algorithm)同国内外权威反算软件对3种典型路面结构的3组FWD实测弯沉盆数据进行模量反算比较[7]。

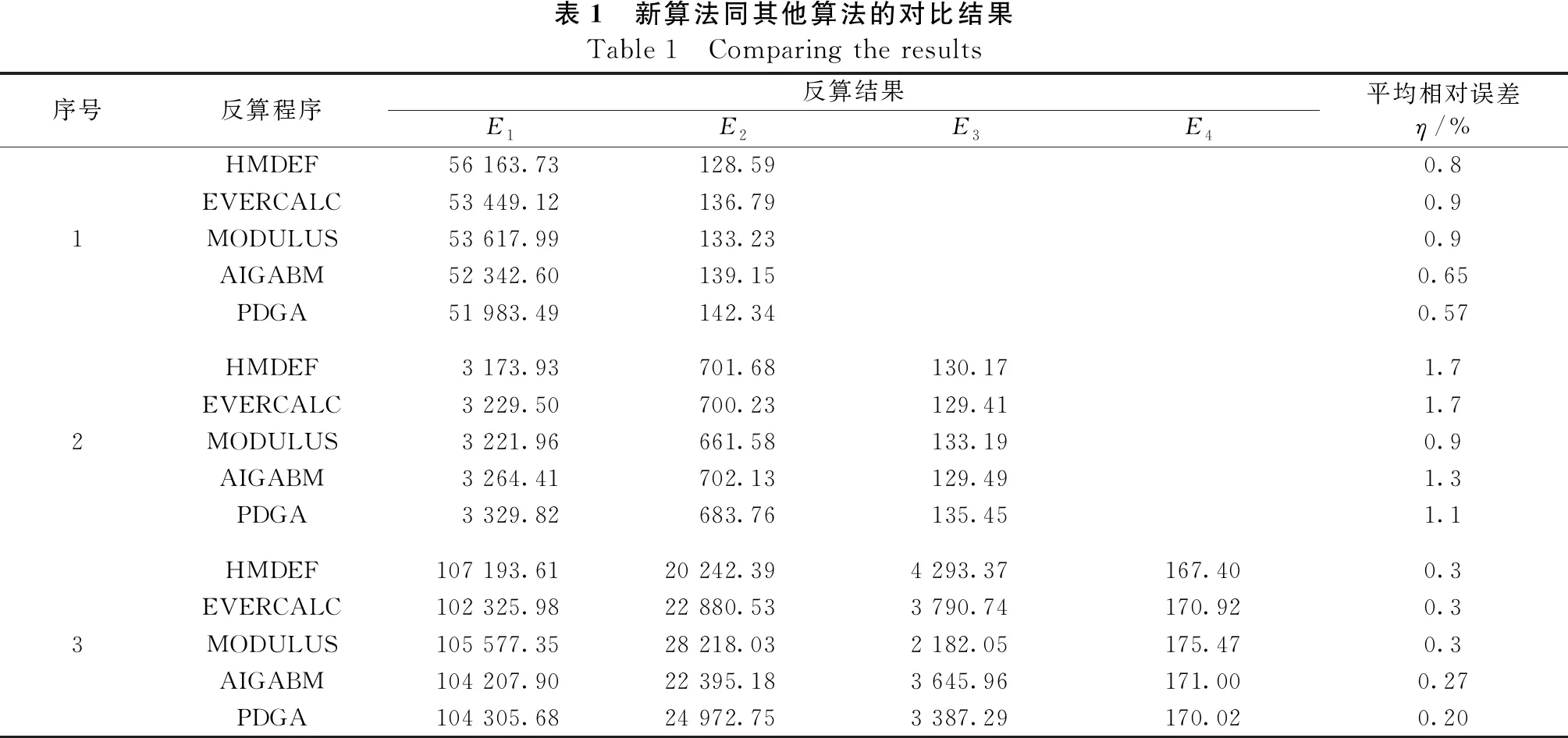
表1 新算法同其他算法的对比结果Table 1 Comparing the results序号反算程序反算结果E1E2E3E4平均相对误差η/%HMDEF56 163.73128.590.8EVERCALC53 449.12136.790.91MODULUS53 617.99133.230.9AIGABM52 342.60139.150.65PDGA51 983.49142.340.57HMDEF3 173.93701.68130.171.7EVERCALC3 229.50700.23129.411.72MODULUS3 221.96661.58133.190.9AIGABM3 264.41702.13129.491.3PDGA3 329.82683.76135.451.1HMDEF107 193.6120 242.394 293.37167.400.3EVERCALC102 325.9822 880.533 790.74170.920.33MODULUS105 577.3528 218.032 182.05175.470.3AIGABM104 207.9022 395.183 645.96171.000.27PDGA104 305.6824 972.753 387.29170.020.20

从反算结果来看，本文提出的PDGA反算方法结果精度均有所提高，从而有效地说明了本文新算法反算结果高精度的特点。此外，该算法具有遗传算法和差分进化算法的所有优点。且反算只要给出各变量取值范围，无需进行初值选取，算法稳定性较高。

由于算法用传感器读数作为权，对传感器读数具有一定的误差容忍性。这里，将文献[7]中的每个弯沉数据加上随机误差。其中，随机误差由均值为0，标准差为2 μm的正态分布[14]发生器模拟产生(见表 2)。

在有随机误差的情况下，从反算结果(如表 3所示)可以看出，与AIGABM算法相比，PDGA算法在处理随机误差时，具有一定的鲁棒性。

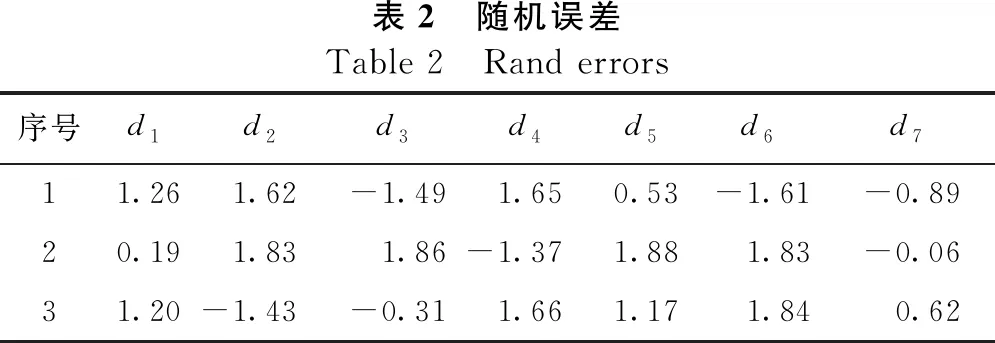
表2 随机误差Table 2 Rand errors序号d1d2d3d4d5d6d711.261.62-1.491.650.53-1.61-0.8920.191.831.86-1.371.881.83-0.0631.20-1.43-0.311.661.171.840.62

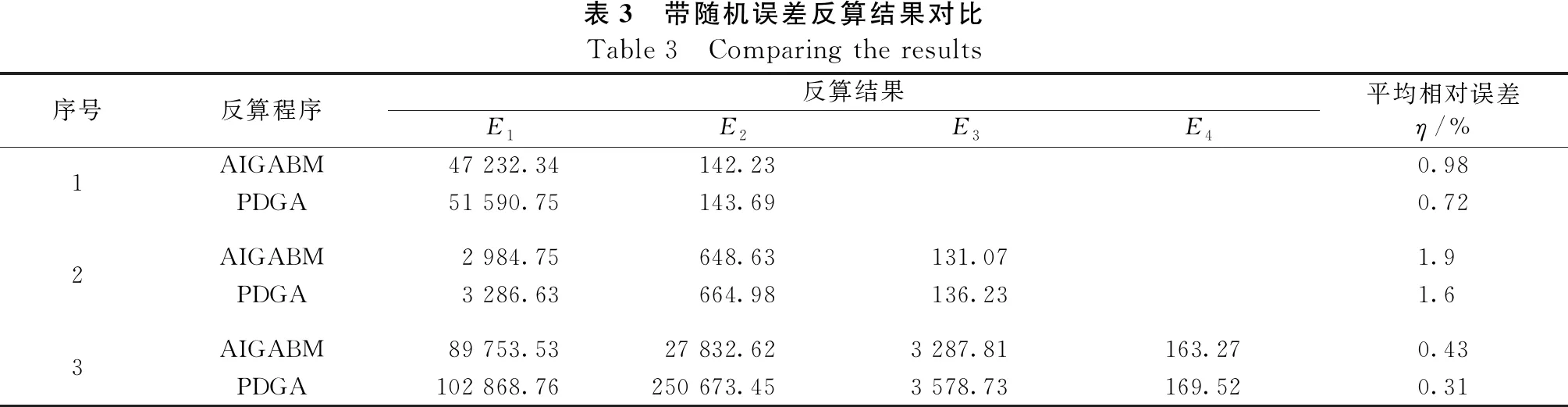
表3 带随机误差反算结果对比Table 3 Comparing the results序号反算程序反算结果E1E2E3E4平均相对误差η/%1AIGABM47 232.34142.230.98PDGA51 590.75143.690.722AIGABM2 984.75648.63131.071.9PDGA3 286.63664.98136.231.63AIGABM 89 753.5327 832.623 287.81163.270.43PDGA102 868.76250 673.453 578.73169.520.31

3 工程实际应用

为了考察本文算法的实用性，本文用某高速公路沥青砼路面实测数据做模量反算计算分析。路面组成如下：① 面层:上面层为5 cm SMA-16或SAC-16，中面层为6 cm AC-20I，底面层为7 cm AC-25I；② 基层：20 cm 5%～6%水泥稳定碎石+20 cm 5%～6%水泥稳定碎石；③ 底基层：4%水泥稳定碎石20 cm。

反算分3层进行，即18 cm沥青砼面层作为面层，基层和底基层(共60 cm)作为基层，土基作为土基层(厚度为∞)。泊松比参数按照《公路设计手册(路面)》的取值范围：沥青混合材料0.35；水泥混凝土0.2；水泥稳定类材料0.20；路基0.40。FWD落锤盘直径为30 cm，各传感器距荷载中心的距离分别为0、203、305、457、610、914、1 219、1 524、1 829 mm。检测时采用一级荷载，设定标准荷载为50 kN。在计算过程中，群体大小为100，遗传操作交叉概率为0.95，变异概率为0.015，锦标赛选择参数为0.05；差分进化操作中缩放因子为1，概率交叉因子为0.5。从反算结果(见表 4)来看，本文所提出的PDGA算法所反算的结果精度EVERCALC保持高度一致，并且其统计特征要优于EVERCALC的结果。

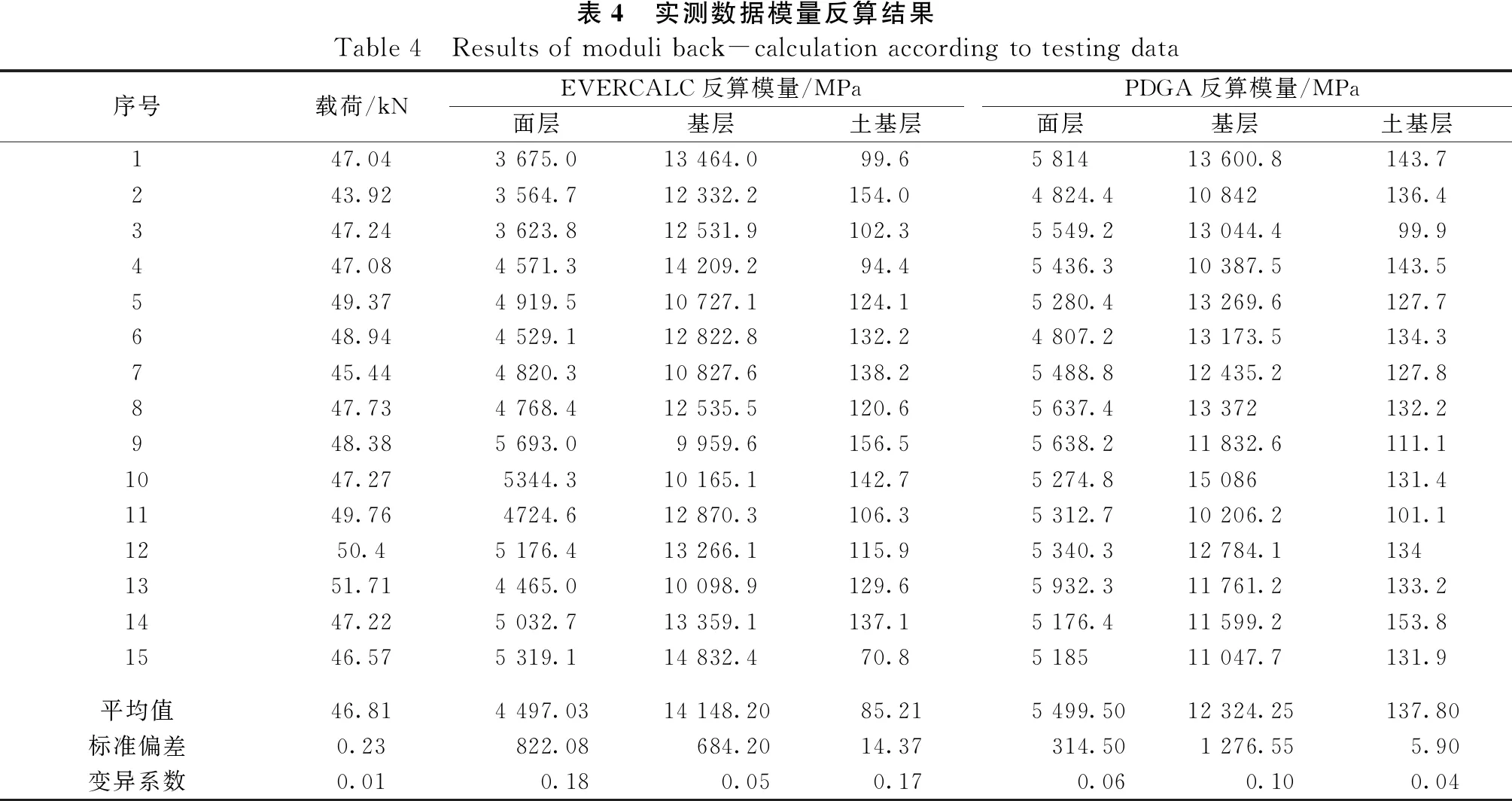
表4 实测数据模量反算结果Table 4 Results of moduli back-calculation according to testing data序号载荷/kNEVERCALC反算模量/MPaPDGA反算模量/MPa面层基层土基层面层基层土基层147.043 675.013 464.099.65 81413 600.8143.7243.923 564.712 332.2154.04 824.410 842136.4347.243 623.812 531.9102.35 549.213 044.499.9447.084 571.314 209.294.45 436.310 387.5143.5549.374 919.510 727.1124.15 280.413 269.6127.7648.944 529.112 822.8132.24 807.213 173.5134.3745.444 820.310 827.6138.25 488.812 435.2127.8847.734 768.412 535.5120.65 637.413 372132.2948.385 693.09 959.6156.55 638.211 832.6111.11047.275344.310 165.1142.75 274.815 086131.41149.764724.612 870.3106.35 312.710 206.2101.11250.45 176.413 266.1115.95 340.312 784.11341351.714 465.010 098.9129.65 932.311 761.2133.21447.225 032.713 359.1137.15 176.411 599.2153.81546.575 319.114 832.470.85 18511 047.7131.9平均值46.814 497.0314 148.2085.215 499.5012 324.25137.80标准偏差0.23822.08684.2014.37 314.50 1 276.555.90变异系数0.010.180.05 0.170.060.100.04

4 结论

本文结合自适应信息遗传算法和差分进化算法各自的优势，提出了以信息差分遗传算法来反算路面模量的新方法。计算结果表明，该方法反算过程稳定收敛且可达到满意的精度。在传感器存在随机误差的前提下，本算法反映出了较强的鲁棒性。随着计算机技术的发展，此类优化方法在求解复杂优化问题上具有独特的优势。计算表明，该算法在路面模量反算中具有较强广阔的应用前景。