不同边界条件下扒杆结构强度及变形对比分析

贺 幸，杨培青

(1.九江市港口航运管理局, 江西 九江 332000； 2.中国船级社 上海规范研究所，上海 200135)

0 引言

随着我国风电产业、基建行业的发展，越来越多的起重船被建造和投入使用。扒杆作为起重船上最为重要的结构，其强度问题一直备受建造者及使用者的关注。在扒杆强度分析领域，学者们已经做了大量研究工作。张云志[1]基于某内河150 t起重打捞船扒杆，根据中国船级社规范，采用有限元的方法校核了典型工况下扒杆的强度及稳定性；吴英照[2]以某内河船100 t起重船起重扒杆为研究对象，综合考虑了包括起吊载荷、起升角度、风载荷、船舶倾斜等因素，对扒杆作业工况下结构强度进行了评估；王贵彪等[3]基于MSC.PATRAN/NASTRAN软件对内河B级航区的120 t起重船扒杆进行了结构强度及稳定性研究，并提出了部分结构加固改进措施和注意事项；庞君等[4]以某250 t起重船为研究对象，通过直接计算的方法评估了其作业状态下的强度和稳定性；周国宝等[5]、徐逸舟等[6]均基于不同型号与不同起吊载荷的扒杆，采用有限元直接计算法进行了扒杆结构强度分析。

对比上述文献发现，对于扒杆的边界条件均是采用沿钢丝绳方向施加线位移约束的方式。为了能够更加准确地模拟扒杆在实际作业过程中的受力情况，本文以某内河4 000 kN起重船为研究对象，基于《船舶及海上设施起重设备规范》(2007)(下文简称《起重规范》)和《起重设备法定检验技术规则》(1999)(下文简称《起重法规》)等规范，采用建立扒杆钢丝绳取代沿钢丝绳方向施加线位移约束的方式来校核该船的扒杆强度，将2种约束得出的有限元结果进行对比，为扒杆结构强度评估方法提供一定参考。

1 有限元模型

本文所分析的起重船扒杆模型为左右对称结构，采用有限元分析软件MSC.PATRAN建立扒杆模型。模型中所有板架结构、主杆、加强板均采用二维3、4节点壳单元模拟，其他支撑管件及型材用2节点梁单元模拟。模型材料参数如下：弹性模量2.06×105MPa，泊松比0.3，密度7.85×103kg/m3。扒杆模型节点数166 515个，单元数172 362个。扒杆整体模型见图1、图2。

图1 扒杆整体模型图

图2 扒杆模型俯视图

本模型坐标系为：坐标系统的原点取在扒杆根部；X轴为沿臂架所在平面，由扒杆根部指向扒杆头部为正；Y轴由原点指向扒杆根部左侧轴套的中心点；Z轴垂直于扒杆平面向上。

2 计算工况及边界条件

2.1 计算工况

根据《起重规范》及该船的起重系统受力计算书，本文挑选的典型计算工况见表1。

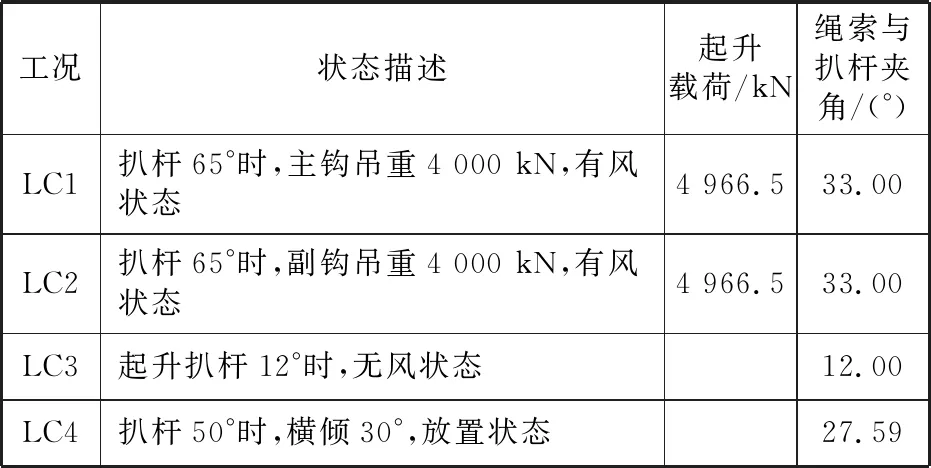
表1 典型计算工况

2.2 边界条件

本文采用2种不同边界条件对同一扒杆进行强度分析，分别见表2、表3。2种边界条件在扒杆底端连接处一致，均采用放开船宽方向的转动自由度，约束其余自由度的方式。2种边界条件不同点在于扒杆顶端拉索处与钢丝绳端点处的约束形式。

表2 第1种约束方式

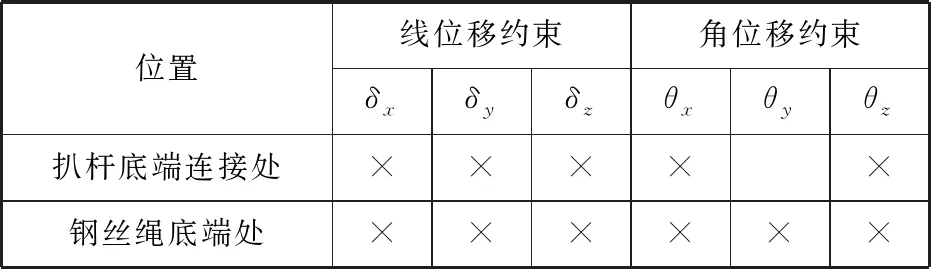
表3 第2种约束方式

第1种约束方式比较常见，在大部分文献中均有记载。本文主要对第2种约束方式进行分析，约束方式见图3、图4。

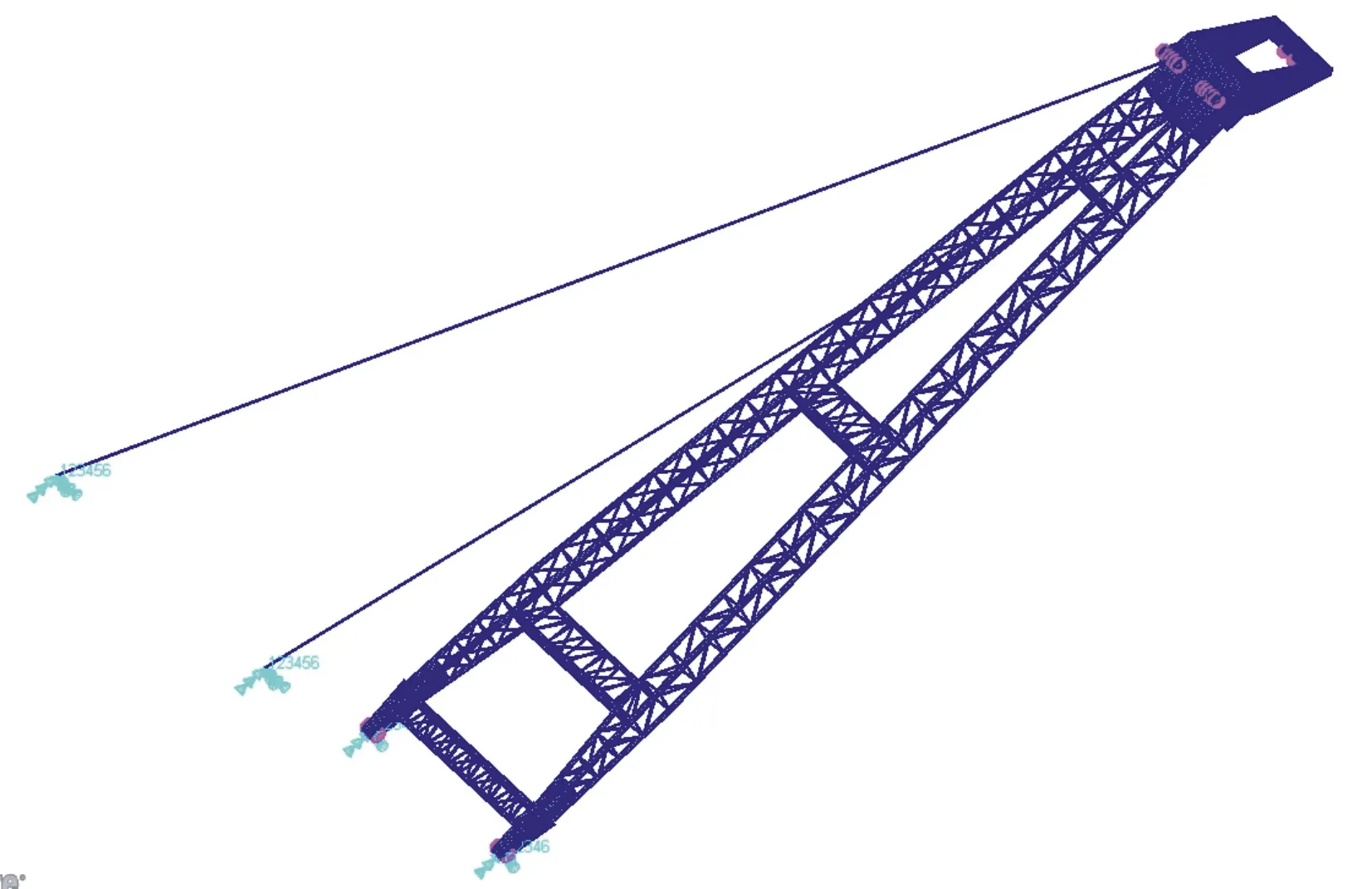
图3 第2种约束方式整体图

图4 第2种约束方式局部图

本文钢丝绳采用Rod单元模拟，该单元可以承受轴向载荷的扭转载荷的作用。本起重船钢索型号为44ZAA-8X36SW-IWR-1770 GB 8919—1996，共有8股绳索；股绳索由36根钢丝拧成，钢索弹性模量为1.45×105MPa。

3 计算结果及分析

根据MSC/NASTRAN软件计算得到4种工况、2种约束方式下扒杆的应力值与变形值，结果见表4。

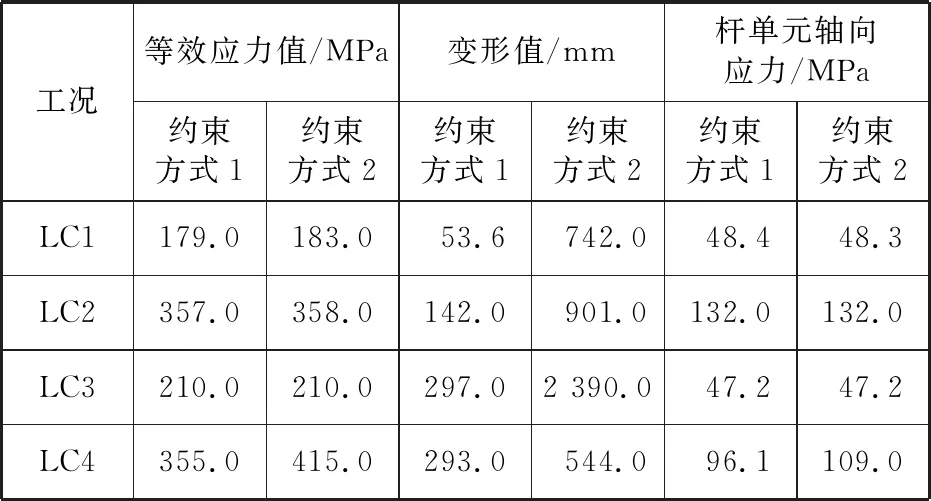
表4 2种边界方式分析结果汇总

从表4发现，等效应力最大差值为60 MPa，杆单元轴向应力最大差值为12.9 MPa，且应力最大差值均出现在工况LC4，即扒杆50°放置状态、船舶横倾30°的极限工况，其余工况的应力差值较小。对比2种约束情况下最大应力值位置可以发现，两者最大应力值除了数值的差别外，最大值所处位置一致，可以看成2种约束形式在力学上达到的效果是一致的。

对比2种约束形式的变形情况发现，第2种约束方式的变形值均大于第1种。这是由于第2种约束方式考虑了绳索弹性模量的影响，差值最大值出现在起升工况。2种约束情况下，横倾30°工况扒杆整体的变形情况见图5～图8。

由图5、图6可以看出，2种约束形式下扒杆在Y向的变形差距较大。采用第1种约束形式扒杆头部由于未考虑钢索的影响，被强行约束住；而第2种约束的变形更加贴近现实，由扒杆头部开始向Y向偏移。

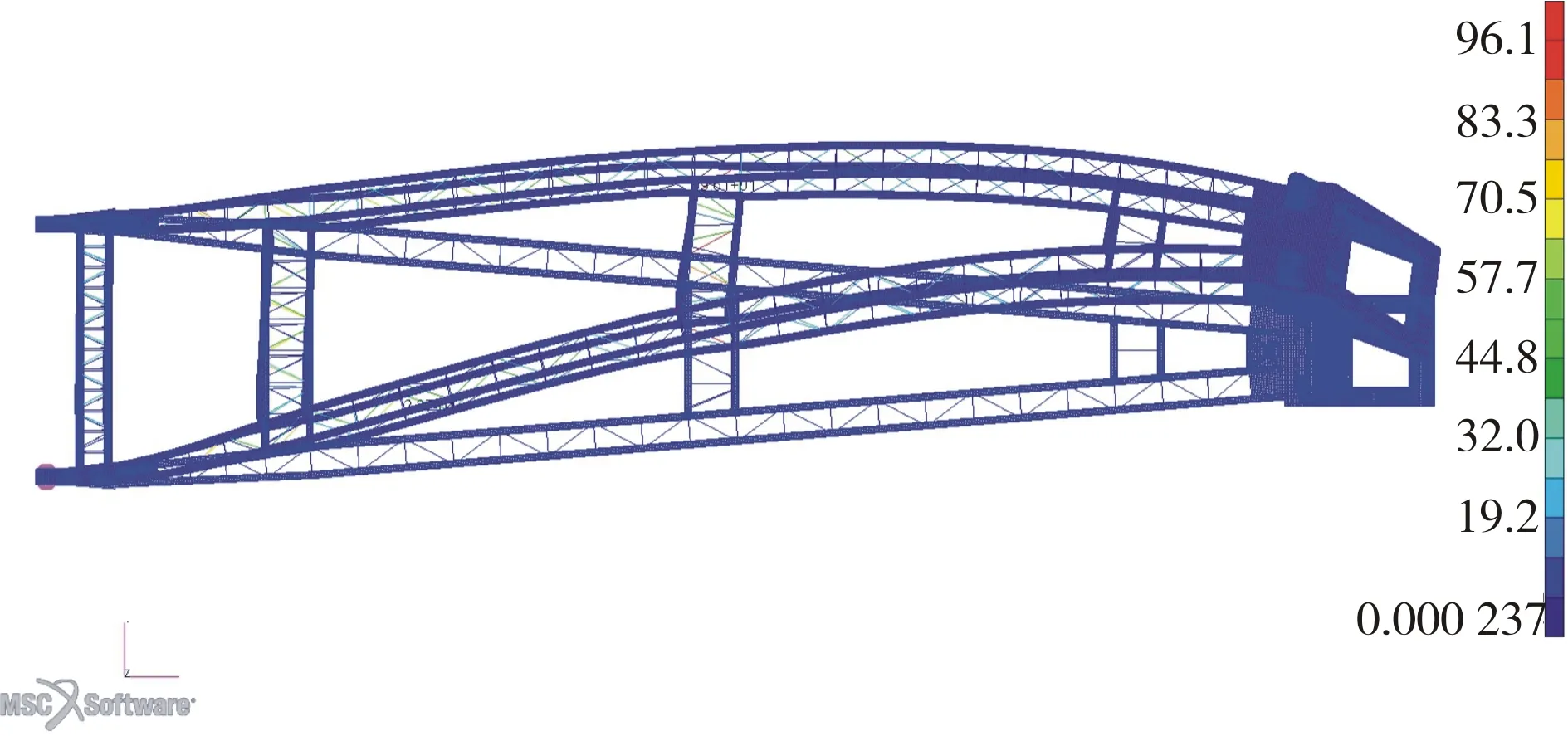
图5 第1种约束下扒杆变形(俯视图)(单位：MPa)

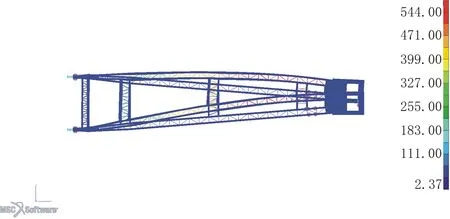
图6 第2种约束下扒杆变形(俯视图)(单位：MPa)

由图7、图8对比看出：当采用约束方式1时，扒杆Z向没有产生出较大的变形；而约束形式2，即采用钢丝绳索模拟扒杆的受力情况时，扒杆呈现出明显的下沉情况。

图7 第1种约束下扒杆变形(侧视图)(单位：MPa)

图8 第2种约束下扒杆变形(侧视图)(单位：MPa)

第1种约束方式采用局部坐标系约束的方式，方向是沿着扒杆绳索的方向，将该方向的约束分解可以得到Z向的约束，即采用该种方式放大了扒杆顶部在Z向受到的约束。采用第2种约束形式，即建立钢丝绳索的方式，将约束施加在钢丝绳索端部，能更加准确模拟扒杆的受力情况。在扒杆真实的受力过程中，扒杆顶部是处于一个相对自由的状态，仅靠钢丝绳索固定。当船体运动幅度较大时，扒杆的运动趋势也会增加，此时钢丝绳会产生一个阻止扒杆运动的绳索拉力。钢丝绳有一定的变形幅度。当扒杆运动状态较大时，钢丝绳受力较大，绳索的变形也会增加。随着钢丝绳的变形，扒杆的角度也会产生一定的变化。和约束形式1的刚性约束相比，约束形式2是一种柔性约束。该方式考虑了绳索变形情况的耦合，并且绳索约束的形式并不会将头部约束的自由度完全固定，更加贴合实际的受力情况。正是这两种约束的差异导致了在横倾较大工况时，扒杆变形的差异。

4 结论

本文基于某内河4 000 kN起重船，对比了2种约束方式下扒杆结构强度，现得出结论如下：

(1)在普通吊装工况及过桥工况下，2种约束方式对应扒杆的应力情况基本相似，故在吊装及过桥工况下2种约束形式都可以用来分析扒杆强度。

(2)当船体出现较大的横倾工况时，如本文所分析的横倾30°极限工况，2种约束方式的应力分析结果差距较大。这是由于采用第1种约束形式代替钢丝绳完全固定了扒杆的运动情况，扒杆变形小于实际情况，致使横向变形较小未能达到实际状态。

(3)对比2种约束形式来看，2种约束对扒杆的应力分析基本相似，在应力分析方面均能准确呈现应力分布状态；在扒杆变形分析方面，约束形式1缩小了扒杆的变形，约束形式2放大了扒杆变形。由于在实际过程中绳索起升装置会一直拉动绳索，不会出现扒杆整体下沉较多的情况，故在分析变形时建议结合约束1和约束2的结果进行研究。