华东区域中尺度集合预报系统的改进及2020年梅雨期降水试验

谭燕 黄伟 杨玉华 张旭 陈葆德 2

1 中国气象局上海台风研究所, 上海 200030

2 中国气象局台风数值预报重点实验室, 上海 200030

1 引 言

经过近半个世纪的发展，集合预报的研究已经从全球大尺度数值预报扩展到中尺度区域数值预报，甚至更小尺度的对流尺度数值预报（Clark et al.,2009; Kain et al., 2013）。模式的时空分辨率更为精细，集合扰动的技术也更为全面，集合预报已经逐步从研究领域向业务预报部门推广应用，并取了良好的应用成效（Schwartz et al., 2015; Swinbank et al., 2016）。而这其中，短期的中尺度区域集合预报是这十多年来从研究领域向应用领域转化的热点，虽然国内外的研究成果颇丰，但却很难取得重大的根 本 性 的 进 展（Hacker et al., 2011; Jankov et al.,2017）。难点可能有两方面的原因：其一是与区域集合预报关注的预报对象有关，因为区域模式更多地关注中小尺度高影响天气的发生发展，而这类天气过程的空间尺度小，生命史短并且移动迅速，且伴随着强烈的突发性和转折性，同时与大尺度环境场之间还存在着复杂的相互作用，其物理和动力的机制较为复杂（孙建华等, 2013），此外，中小尺度天气系统还会受到如地形等局地环境因素的影响（Volker et al., 2008），所以要想全面地认知这类高影响天气的本质仍然需要时间。其二来自集合方法本身，我们知道，集合预报研究的核心问题即集合扰动方法的研究，当今成熟的集合扰动方法是针对大尺度的天气过程提出，以大尺度的斜压不稳定理论为基础，有着明确的物理含义（Buizza et al.,2005），而对中小尺度的天气对象而言，其动力过程是以对流不稳定为主，误差增长和发展的方式与大尺度过程截然不同（Mass et al., 2002; Grimit and Mass, 2002），对一种尺度适合的扰动方法对其它尺度并不一定适合，这就使得构造合理的集合扰动难度增大，以至于现有的各类扰动方案是否同样适用于中小尺度天气过程至今仍没有统一答案。近十年来，大量的研究来探讨初始误差、模式误差，以及侧边界条件的重要性问题，评估各类扰动方案在区域集合预报系统中的作用（Ha et al., 2015; 刘畅等, 2018），业务应用上也取得了很好的效果，例如：美国空军的中尺度集合预报系统（The U.S. Air Force Weather Agency’ s mesoscale ensemble；Hacker et al., 2011）采用分辨率为45 km和15 km的两层嵌套方式来构建10个集合成员，测试各类不同的扰动方案，发现通过集合后，其效果明显优于控制预报，且任意一种集合扰动方法所构建的集合预报均比直接降尺度全球集合的效果好，其中初始场的扰动会对12 h之内地面要素的预报有显著影响；采用随机物理扰动方案，会比多物理参数化组合的效果好，后者的影响主要体现在边界层附近；当同时结合多种随机物理扰动方案时，效果最优。同样的，在分辨率为13 km的北美快速更新集合系统（North American RAP Ensemble；Jankov et al.,2017）和分辨率为15 km的GRAPES中尺度集合预报系统中（张涵斌等, 2014; Xu et al., 2020）也开展了类似的工作。此外，对于区域模式所面临的侧边界条件的不确定性问题，已有的研究大都表明，有必要对集合成员的侧边界进行扰动（Nutter et al.,2004a, 2004b; Hohenegger and Schär, 2007;Hohenegger et al., 2008; Saito et al., 2012）。其中最直接的方法即从全球集合预报或较大尺度的集合预报中获取侧边界资料，为较小尺度的集合预报各成员提供侧边界条件，如Nutter et al.（2004a, 2004b）采用该方法发现侧边界条件的扰动能够迅速地传遍整个嵌套区域，从而改善区域集合的离散度；Hohenegger et al.（2008）后续指出：随着预报时效的延长，侧边界扰动的影响可以叠加到初始场的扰动上，从而改善集合系统的预报性能。

整体而言，当综合地考虑各类不确定性的来源，集合系统的离散度会增加，对强降水和地面变量的预报能力会显著提升。然而，在各类扰动方案的比较研究中，Hamill and Whitaker（2011）也指出：增加的各类误差，在一些情况下，不仅会抑制集合离散度的发散，还会使得集合平均的误差增大，效果适得其反。总的来说，怎样结合各类扰动方法，构建一个有效的中尺度集合预报系统，与模式系统自身有着密切的关系。如何针对区域数值预报中的不确定性构建有效的区域集合扰动方法，初始误差、模式误差、以及侧边界条件的作用如何考虑，以及他们相对于模式分辨率和天气系统时空尺度的配置等，仍然是值得深入研究的问题，也是集合预报技术在业务应用中的关键点。

华东区域中尺度集合预报系统（SWARMSENV1）自2010年在华东区域气象中心投入业务应用，主要用于支撑3～5天的短期预报。在常年的应用和检验中，发现SWARMS-ENV1也存在着大多数集合预报系统的通病之一，即系统发散度不足（Stensrud et al., 1999; Buizza et al., 2005; Romine et al., 2014），从而使得集合预报系统不能有效地体现预报的不确定性，使用效果往往达不到预期。

SWARMS-ENV1采用增长模繁殖向量来表征初始场的不确定性；同时通过数值试验，最终选取三类积云对流参数化方案（Kain-Fritsch new方案、Betts-Miller-Janjic方 案 和Grell-Devenyi ensemble方案）、两类地表参数化方案[Monin-Obukhov方案和Monin-Obukhov（Janjic）方案]以及2类边界层方案（MYJ方案和YSU方案）进行优化组合（Skamarock et al., 2008），最终形成21个集合成员。短期集合预报常用上述多物理参数化方案的组合来表征模式的不确定性，一方面，因各种参数化方案之间的差异性较大，可增加集合的离散度，有助于提升预报技巧（Berner et al., 2011, 2015），但另一方面，该方法在理论和实际应用上也存在着明显的缺点。Knutti et al.（2013）的研究明确指出：从统计学的角度看，集合预报所添加的小扰动应满足随机变量的统计特征，即变量之间是相互独立且满足一定的概率密度分布，集合预报所表征的预报不确定性是随机的预报误差随时间演化的结果，而多物理参数化方案并不符合这一前提，不同的物理参数化方案之间的物理假定、触发机制、概念模型等均存在差异，不同方案也有各自不同的气候特征和系统性的误差分布特征（Jankov et al., 2017），从而导致系统偏差或成员聚类（Johnson et al.,2011）。此外，要发展和运维多套物理参数化方案也要耗费大量的资源，目前，各大数值预报中心所采用的主流模式扰动技术均为随机物理扰动方案，（Palmer et al., 2009; Charron et al., 2010; Bouttier et al., 2012; Weisheimer et al., 2014; Zhou et al., 2017）因此，随着现今随机物理扰动方案受到越来越多的关注，有必要进行新的尝试。

中国气象局上海数值预报模式系统（CMASH9）于2015年底完成升级，无论是对高低空形势场预报还是降水预报，其预报性能均得到明显改善（徐同等, 2016），这为中尺度集合预报系统的升级提供了优良的基础。本文希望以CMA-SH9的初始场作为控制预报，并在此基础上开展中尺度集合预报试验：一方面充分地利用全球集合预报的信息来构造区域集合的初始扰动和侧边界扰动，从而整体上提升区域集合预报系统的预报精度；另一方面针对集合离散度偏低的现象，开展随机物理倾向扰动方案的参数优化试验，确定适合模式配置的最优参数，最大可能地表征模式的不确定性，从而提高集合系统离散度；并最终通过批量试验来全面地评估集合预报系统升级前后的预报能力。本文的结构安排如下：第二部分介绍华东区域中尺度集合预报系统的概况以及本文所进行的集合试验的设计和检验所用的资料；第三部分评估为期一个月的梅雨期试验结果；第四部分简要给出典型个例的降水预报；最后为小结与讨论。

2 集合预报系统与资料

2.1 集合预报系统介绍

华东区域中尺度集合预报系统（SWARMSENV1，以下简称V1）于2010年建成并投入业务使用，系统的主要特点可以概括为：采用增长模繁殖法和多种物理参数化方案的组合，构建21个集合预报成员，预报范围如图1中虚线区域所示，模式水平格点数为159×159，水平分辨率15 km，垂直方向27层，控制预报的初始场使用ADAS（ARPS Data Analysis System；Brewster, 1996）提供的分析场，侧边界条件为NCEP全球预报系统（Global Forecast System，简称GFS）的预报场，侧边界条件每6小时更新一次，每日00:00和12:00（协调世界时，下同）启动，进行120小时预报，结果每小时输出一次。

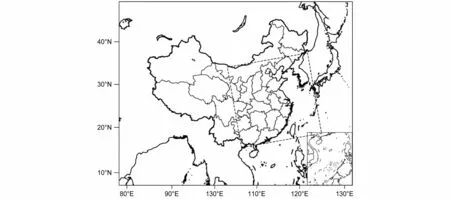
图1 第一代中尺度集合预报系统（SWARMS-ENV1，简称V1，黑虚线）与扩展区域后第二代中尺度集合预报系统（SWARMS-ENV2，简称V2）的预报范围Fig. 1 Horizontal domain of SWARMS-ENV1 (V1) model (black and dashed) and the expanded domain of SWARMS-ENV2 model (V2)

升级后的华东区域中尺度集合预报系统（SWARMS-ENV2，以下简称V2），其预报范围如图1所示，控制预报的初始场同中国气象局上海数值预报模式系统（CMA-SH9），侧边界通过降尺度NCEP全球集合预报系统（Global Ensemble Forecast System，简称GEFS）的控制预报获取，模式水平格点数为760（纬向）×600（经向），水平分辨率为9 km，垂直方向51层。模式选用Thompson双参数云微物方案、RRTMG长短波辐射参数化以及YSU边界层参数化方案（Zhang et al., 2021）。模式通过ADAS客观分析系统和复杂云分析技术实现对观测资料的同化，目前ADAS同化的观测资料主要包括常规探空观测和地面自动气象站观测，后者包括常规地面观测（SYNOP）、船舶观测（SHIP）、机场地面报（METAR）、浮标（BUOY）、飞机观测（AMDAR）等；同时模式利用复杂云分析技术对新一代天气雷达（China new generation weather radar，简称CINRAD；李柏等, 2013）的SA、SB、SC波段雷达的反射率进行同化。表1给出升级前后华东区域中尺度集合系统的基础配置情况。

表1 华东区域中尺度集合预报系统Table 1 The setup of regional ensemble forecast system

采用动力降尺度方法来获取集合预报的初始扰动场，是一种直接且简单有效的方法（Bowler and Mylne, 2009; Montani et al., 2011; Kühnlein et al.,2014），当今一些中尺度集合预报系统（如COSMOLEPS、MOGREPS）也均有所采用，其模式分辨率从9～25 km不等，甚至有研究直接将其用于更高分辨率的对流尺度模式中（Peralta, 2012）。GEFS采用集合卡尔曼滤波（EnKF）方法（Zhou et al.,2017）来表征大气初始时刻预报的不确定性，同时引入随机物理倾向扰动来表征模式的不确定性，生成21个集合成员。V2的集合初始扰动生成分为三个步骤：第一步，通过动力降尺度方法直接将GEFS全球集合预报系统的初值场和预报场插值到区域模式的分辨率和范围，从而形成区域模式积分所需的初始场和侧边界条件。第二步，计算降尺度后各集合成员（Vien）与控制预报（Vc）的差，从而形成各变量的扰动场（Pien），如公式（1）所示，其中扰动变量包括：风场、气压场、温度场和湿度场；第三步，将CMA-SH9同化后的分析场（Va）作为V2的控制预报，在其基础上，将（1）式得到的扰动场与其进行融合，从而形成新的集合初始扰动场（VPien）。在这个过程中，由于初始扰动和侧边界条件均来自GEFS，也从一个侧面避免了两者之间的不协调、激发虚假波动等问题（Caron, 2013）。

其中，Vi表示集合成员，Vien表示直接动力降尺度得到的各成员的物理量场，Vc为GEFS全球集合控制预报降尺度后的初始场，Pien是各物理量的扰动场，Va为CMA-SH9同化后的分析场（同时也是V2控制预报的初值场），VPien为融合以后新的集合初始场，ien=（1, 2, ···,M）为集合成员序号，M为集合成员数（M＝20）。

2.2 随机物理倾向扰动方案（SPPT）的优化

模式物理过程的倾向项用于表征不能被数值模式解析的次网格物理过程的总体效应，这类过程包含辐射、微物理、深对流、浅对流和边界层过程。Buizza et al.（1999）首次提出将随机扰动加入模式物理过程的倾向项中来体现次网格物理过程的不确定性，即随机物理倾向扰动方案（Stochastically Perturbed Parameterization Tendencies， 简 称SPPT），Berner et al.（2015）在 前 人 的 基 础 上（Palmer et al., 2009），将该 方案 引 进 至WRF模式中，并在实际业务预报中取得了较好的效果（Sanchez et al., 2016; Kevin et al., 2020）。

其中，Xphys表示温度、纬向风、经向风和湿度等参数的倾向，r(x,y,t)是一个与时间与空间相关的随机扰动场，x、y和z分别表示经度、纬度和时间。每个格点上的随机数满足均值为0，方差为σ2的高斯分布，且|r|≤1。将随机扰动场r(x,y,t)通过二维傅里叶展开，得到：

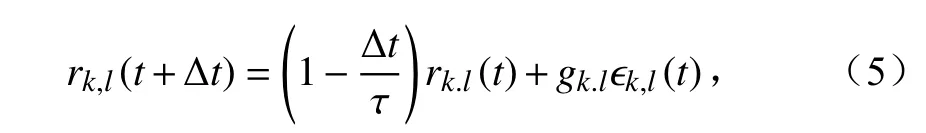
式中，

通过上述一系列的数学变换，可以看到，SPPT方案中有三个参数会影响到随机扰动场的形态，即格点方差（σ2下文记作A）、随机扰动场的去相关时间（τ，下文记作T）和随机扰动场的去相关空间（k，下文记作L）。已有学者对SPPT方案中的各参数在不同天气尺度背景下对预报变量所起的作用进行研究（Bouttier et al., 2012; 袁月等,2016; 闵锦忠等, 2018; 徐致真等, 2019），但研究成果很大程度上依赖于所研究的动力系统，至今仍没有明确的结论，因此仍然需要根据具体的模式配置和关注的预报对象进行大量的适应性试验。

本文选取两个典型个例，一是2019年11月23～25日强降温个例，其影响系统的水平尺度相对较大，约有上百千米；二是2020年6月15～17日强降水个例，其影响系统为水平尺度200 km内的中尺度涡；这两类天气发生的季节不同，影响系统的特征尺度也存在差异，上述三个参数对预报的影响如何？参数值的选取是否具有一定的通用性？它们之间怎样的配置可以最大程度地表征V2模式误差的不确定性？为了回答上述问题，设计表2的敏感性试验，其中参考试验REF的参数取默认值，A、T和L为单一要素的敏感性试验，PHY为同时调整三参数的试验，试验中初始场和侧边界条件均不做扰动，取两倍的方差作为临界振幅值；需要说明的是，由于计算资源的限制，表2中各试验的集合成员数均为9。

图2给出表2各组试验离群值（Outlier，数据中有一个或几个数值与其他数值相比差异较大）的时序图，这里选取850 hPa温度场，850 hPa纬向风场和2 m温度场进行分析，试验中成员数取N=9，则理想的离群值即为0.2 [计算公式为2/(N+1)]，越接近理想值则说明系统的可信度越高。可以看到对于不同季节，不同尺度的天气个例，三个敏感参数的表现一致，说明这些参数具有较好的代表性和通用性。它们之间对预报的相对作用各不相同，对格点方差（A）进行改变后，各预报变量均出现了较大的变化，增加方差会系统性的降低离群值，反之，则增加了离群值，说明方差的增加使得集合系统的离散度随之增加，从而使得成员间的差异性增大，反映出更多预报的不确定性。随机扰动场的去相关空间（L）和随机扰动场的去相关时间（T）的改变，对预报的影响较小，与参考预报的结果相差不大，其影响远远小于方差改变带来的影响；但仔细分析也会发现，在夏季个例中，当增加L和延长T时，也会微弱地降低离群值，在一定程度上改进预报的可信度；三个参数对预报的影响大小依次为：A＞L＞T。当PHY试验根据模式自身的配置，合理调整SPPT方案中参数的阈值，并将其进行合理地组合后，在整个预报阶段，系统的离群值与理想的离群值最为接近，说明增强模式中随机物理过程的作用，更能有效地提高集合系统整体的可信度和预报能力。

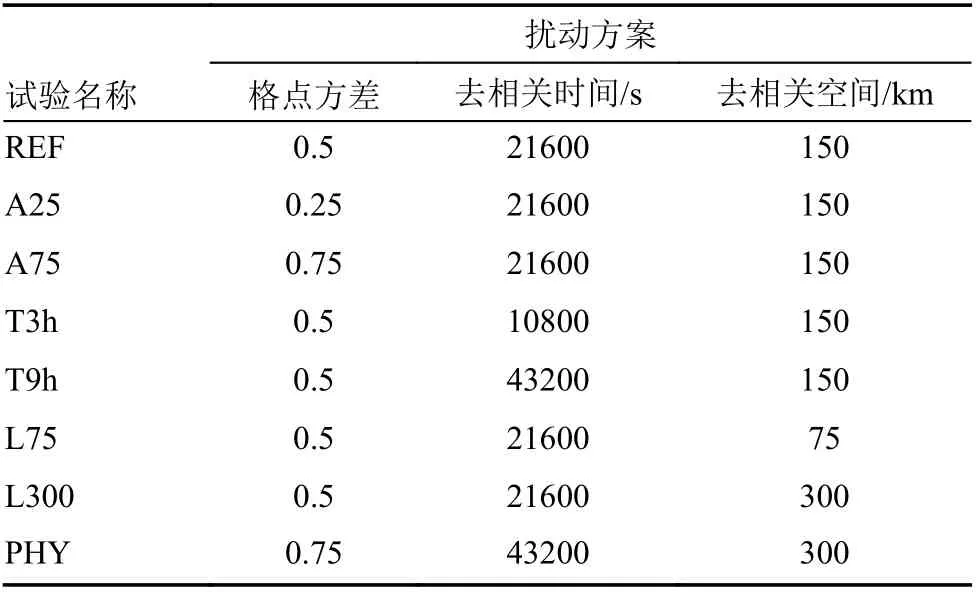
表2 随机物理倾向扰动方案（SPPT）的优化试验Table 2 Sensitive experiment of stochastic parameters

同时，上述变量集合平均的均方根误差随时间的变化（图略）曲线也反映出：在整个预报时段，各组试验集合平均的预报误差均小于控制预报；其中对格点方差进行调整，各变量的预报误差在预报初期就有较明显下调，且随着预报时效的延长，集合平均相对于控制预报改进的幅度更为显著；相对而言，改变扰动的空间尺度和时间尺度，两组误差曲线的走势较为接近，集合平均对控制预报的改进幅度较小。从变量上看，850 hPa纬向风的误差减少最为明显，其次是850 hPa温度和2 m温度。

连 续 分 级 概 率 评 分（Continuous Ranked Probability Score，简称CRPS）可以量化预报变量的累计概率分布函数（CDF）与观测值Heaviside函数之间的差异（Hersbach, 2000），可用于评估集合预报与确定性预报的预报准确率，CRPS越小表示预报准确率越高，理想情况下CRPS等于零，CRPS计算公式为

CRPS的时序图如图3所示，参数间的调整会引起CRPS不同程度的变化。总的来说：对不同的变量，减小方差A，会增加CRPS，反之则会减小CRPS，改变A所引起CRPS的变化幅度最为明显；改变扰动场的去相关空间L和去相关时间T，在不同的预报时刻，两组试验的CRPS曲线在参考预报附近上下波动，其变化幅度均较小。当合理地将参数进行配置后，CRPS值会明显降低，这与图2的结论一致。注意到不同变量的CRPS也有差别：850 hPa温度的CRPS变化区间为0.2～0.7，850 hPa纬向风的变化范围在0.5～1.2，2 m温度的CRPS在1.4～2.1范围内波动，这反映出模式对各变量的预报准确度也存在着差异。同时注意到：冬夏个例之间，SPPT各参数间的影响趋势相似，但从预报的准确度上看，变量之间却存在差异：对于850 hPa的温度和纬向风冬季个例整体CRPS变化区间小于夏季个例，反映出模式对冬季个例中低层的预报准确度更高；而2 m温度的预报，夏季的CRPS评分低于冬季，说明系统对夏季2 m温度的预报技巧更高。

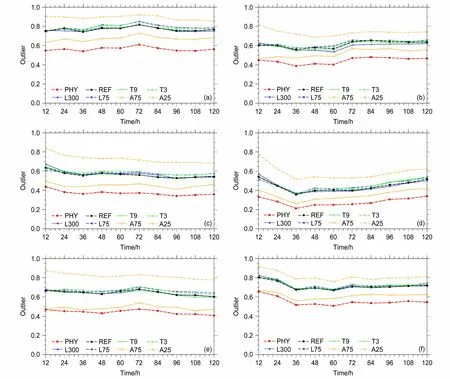
图2 2019年11月23～25日冬季个例（左列）和2020年6月15～17日夏季个例（右列）的各组敏感试验（a、b）850 hPa温度、（c、d）850 hPa纬向风速和（e、f）2 m温度离群值随时间的变化Fig. 2 Time series of the outlier of sensitive experiments for (a, b) 850-hPa temperature, (c, d) 850-hPa zonal wind, and (e, f) 2-m temperature for the winter case from 23 to 25 November 2019 (left column) and for the summer case from 15 to 17 June 2020 (right column)

图3 同图2，为连续分级概率评分CRPS随时间变化Fig. 3 Same as Fig.2, but for CRPS (Continuous Ranked Probability Score)

从上述典型个例的试验及评估结果可见，SPPT方案中参数的选取具有一定的通用性，当根据模式自身的配置来合理调整参数的阈值，可以强化随机过程的影响，对预报起到正效果；为此将试验得到的最优方案引入到V2中，以最大程度地表征V2模式误差的不确定性。

2.3 资料

本文降水预报检验使用图1中SWARMS-ENV1范围内的全国加密自动站资料，该区域内有效站点数超过20000个；同时，地面和高空变量的检验使用同化后的格点分析场资料。需要说明的是，文中V1与V2的比较部分，为了比较的公正性，即将V2的变量值插值到V1的区域进行，其中水平插值方法为双线性插值，垂直插值方法为线性插值，检验统一为V1区域。

3 2020年梅雨期预报性能分析

梅雨是我国汛期重要的天气气候系统，2020年夏季江淮流域经历了一次典型的梅雨季，梅雨呈现出入梅早、出梅晚、梅雨期长、雨区范围广、累计雨量大、强降水过程多的特点（刘芸芸和丁一汇, 2020），一些学者从观测事实出发，对这次超强梅雨的形成原因做了探讨分析（陈涛等, 2020; 张芳华等, 2020）。基于上述典型个例的试验结果，选取此次梅雨季作为研究对象，试验时间为2020年6月7日至7月7日，通过对比分析V1和V2的强降水预报情况，从而加深对系统现有预报能力的认识，也为后续对V2的进一步改进提供科学依据。

3.1 降水预报评分

3.1.1 TS/Bias评分检验

图4给出系统升级前后一个月的梅雨试验的降水TS（Treat Score）评分，图中蓝色为V1的结果，红色为V2的结果。整体而言，TS评分随着预报时效的延长呈下降趋势，对于不同预报时效各量级的降水预报，V2较V1均有大幅度改善。具体来说，对于有无降水的预报，V2在2天之内的预报改善显著，TS评分整体能维持在0.6以上，但之后的预报技巧不及V1，略微下降至0.5左右；但降水一旦发生，V2对降水落区和强度的描述则更为准确，表现为在各时次各量级的TS评分均有所提高。

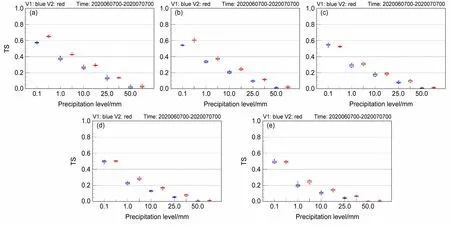
图4 2020年6月7日至7月7日（a）0～24 h、（b）24～48 h、（c）48～72 h、（d）72～96 h和（e）96～120 h累计降水的TS评分箱线图（横坐标为降水量级，蓝色为V1，红色为V2）Fig. 4 Boxplot of Treat Score for 24-h accumulated precipitation from June 7 to July 7, 2020: (a) 0–24 h; (b) 24–48 h; (c) 48–72 h; (d) 72–96 h;(e) 96–120 h. The abscissa is the precipitation level, blue is V1, and red is V2

与此同时，从预报偏差的对比结果看（图5），两个系统的Bias评分均大于1，说明均存在着对各降水量级过度预报的趋势，V1在预报时效96 h之内对大雨及以下量级的预报偏差变化幅度较小，基本维持在1.5上下，对暴雨量级的预报，预报偏差明显增加；V2的偏差在中雨以下量级与V1相当，但对于更大量级的降水，偏差则尤为突出。空报率则从另一个侧面来评估模式预报的准确性，它衡量的是预报将发生的事件中有多少比例在实况中并没有发生，计算发现，V2的空报率相比于V1，在有无降水和小雨量级的预报中，各时次的空报率下降明显；中到大雨的量级，V2的空报率大于V1（图略）。

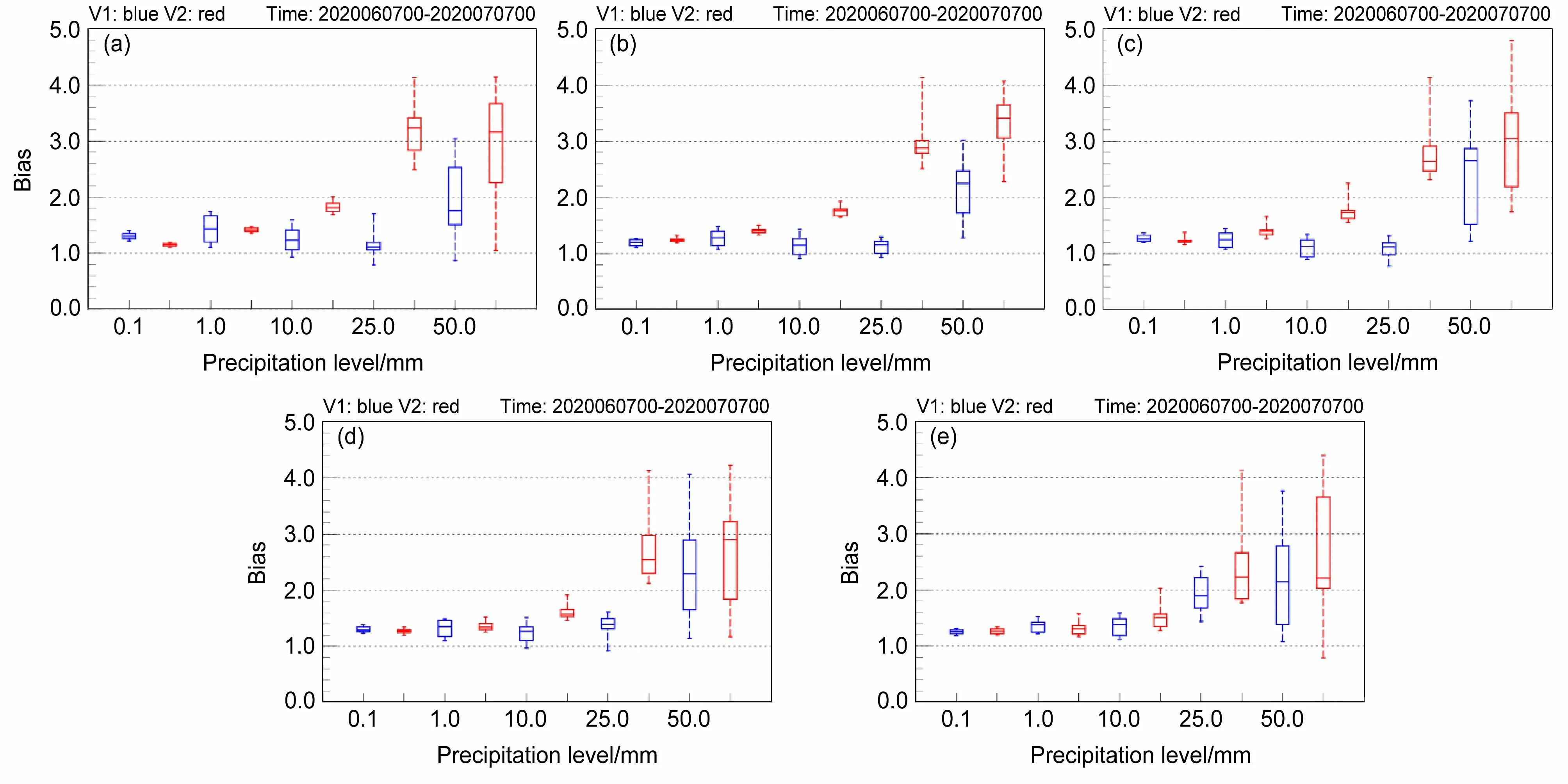
图5 同图4，但为Bias评分Fig. 5 Same as Fig. 4, but for Bias score

3.1.2 BSS评分检验

BSS（Brier Skill Score；Brier, 1950）评 分（−∞，1]之间，其值越大越好，评分为1即表示完美的概率预报，计算公式为

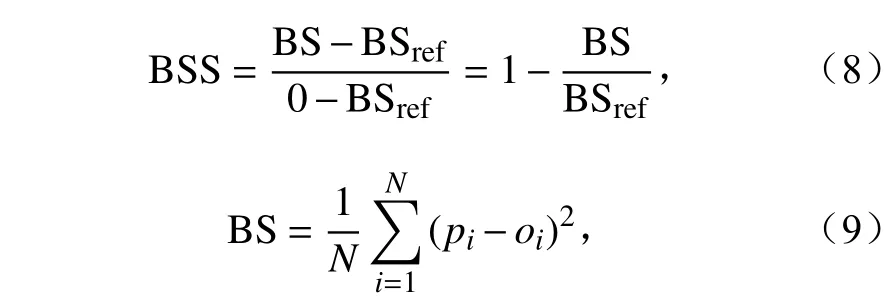
其中，BS为BS评分（Brier Score）， BSref为参考预报的BS评分，这里选取试验期间1个月的平均观测概率作为参考预报，pi为预报概率，oi为观测概率。

图6给出系统升级前后不同预报时效、各降水量级的BSS，图中蓝色为V1结果，红色为V2结果。由图6可见，BSS各时次走势相近，整体而言，相同的预报时效，随着降水量级的增加，评分逐渐降低；同时相同的降水量级，随着预报时效的延长，评分也呈下降趋势。其中，V1对大雨（＜25.0 mm）及以下量级的BSS为正值，说明相对于参考预报，V1对于大雨及以下量级的预报有正技巧；但随着降水强度的进一步加大和预报时效的延长，BSS有负值出现，说明预报技巧有所下降，其中V1对于50.0 mm以上的强降水，除24 h外，各预报时次均缺乏预报能力。反之，V2的BSS曲线对不同的降水量级在各预报时效均为正值，说明相对于参考预报，整体上V2的概率预报更有参考性；同时V2的BSS普遍高于V1，反映出V2的预报准确率较V1均有不同程度的改进。此外，随着降水量级的增加，两组BSS曲线间的差别也逐渐扩大，反映出V2对强降水的概率预报准确率和可信度较V1改善幅度更显著。

图6 2020年6月7日至7月7日24 h累计降水的BSS（Brier Skill Score）评分。横坐标为降水量级，蓝色为V1，红色为V2；图中f120、f96、f72、f48、f24表示预报时效分别为120 h、96 h、72 h、48 h以及24 hFig. 6 BSS (Brier Skill Score) for 24-h accumulated precipitation from June 7 to July 7, 2020. The abscissa is the precipitation level, blue is V1, and red is V2; f120, f96, f72, f48, f24 mean 120-h, 96-h, 72-h, 48-h, and 24-h forecast

3.1.3 ROC曲线

相对作用特征（Relative Operating Characteristic，简称ROC）的原理是将信号探测理论应用到数值天气预报的二分类要素预报的检验中，ROC曲线是对概率预报系统的分级概率分别计算命中率与假警率，用以判断系统的预报准确率（Harvey et al.,1992），在ROC曲线中，曲线位于对角线左上方则可认为系统是具有预报能力（Mason and Mimmack,2002），图中对角线可视为技巧线。由于主要关注集合预报系统在3天以后的降水预报，这里给出新旧两个系统120 h预报时效对不同降水量级的ROC曲线（图7），在其他预报时段结果类似（图略）。由图可见，无论是升级之前还是升级之后的系统，其曲线均位于对角线上方，反映出系统具备了一定的预报能力；同时，ROC曲线与对角线所包含的面积，可用ROC面积表示，这也是衡量系统预报准确率的另一种方式，从图中可以看到，随着降水量级的增加，ROC 面积呈现逐渐减小的趋势。具体到各个降水量级，两个系统对各个分级概率的命中率和假警率变化趋势一致，即随着概率临界值的增加，命中率和假警率也随之增加；对有无降水的预报（图7a），V1的ROC面积大于V2，反映出V1对有无降水的预报准确率更高；当降水量级增加到中雨（图7b），情况则相反，V2的ROC面积大于V1，相比于有无降水的情况，相同概率临界值的假警率普遍大幅降低；大雨量级的ROC评分与中雨类似（图7c）,V2的得分高于V1，且两者的差别更为显现，说明对于较大量级的降水预报，V2的预报准确率更高，这一结果与3.1.2节的结果一致。

图7 2020年6月7日至7月7日新旧系统120小时预报时效（a）0.1 mm、（b）10.0 mm和（c）25.0 mm不同降水量级24 h累计降水的相对作用特征（ROC）曲线（蓝色为V1，红色为V2）Fig. 7 ROC (Relative Operating Characteristic) diagram for 24-h accumulated precipitation of (a) 0.1 mm, (b) 10.0 mm, and (c) 25.0 mm for 120-h forecast period from June 7 to July 7, 2020. Blue is V1, and red is V2

3.2 形势场预报

3.2.1 均方根误差—离散度关系

常用集合平均的均方根误差与集合离散度的关系来探讨集合系统的可信度。对于一个完美的集合系统而言，集合离散度可以反应出随流型变化的预报的不确定性，因此，集合离散度与误差随时间应有相同的振幅和增长率。许多集合系统的发散度都偏低，即表现为预报的不确定性远大于离散度，从而导致预报过度自信（Buizza et al., 2005），图8给出系统升级前后对不同预报变量的集合离散度与均方根误差的变化曲线，两者越接近则说明集合系统的可信度越高。总体上看，V2系统各个变量大部分时次的预报误差均较V1有大幅降低，同时离散度稳步提高，即两者之间的差值在缩小；而相对而言，V1系统对各变量的预报，一方面预报误差较大，另一方面离散度也维持在低位，很难随着预报时效的延长而得到发展，致使两者的差值较大。具体到每个变量，改善最为明显的是850 hPa纬向风，其次是700 hPa相对湿度和10 m纬向风。同时从均方根误差（RMSE）的曲线上可见，V1系统对850 hPa的温度和纬向风的预报存在波动的现象，即有日变化的抖动，这种现象在V2系统中得到缓解，反映出预报更趋于稳定。

3.2.2 Talagrand分布

Talagrand图表是评估集合预报系统常用的工具（Talagrand et al., 1997; Hamill and Colucci, 1997），用于检查观测落在排序后的集合成员预报的相对区间的频数。一个可信的集合预报系统，能较好地表征预报的不确定性，从统计意义上说，观测落在集合成员间的频数是相同的，Talagrand图表则表现为相对平坦的分布。图9给出集合系统对各预报变量120小时的Talagrand分布，根据21个集合成员，可以计算得到观测频率的最优值，即1/22（0.045），当各区间的数值越接近这个最优频率，说明系统成员间的等效性一致，整体性能越好。整体上看，V1的各变量均呈现出明显的U型分布，反应出系统的离散度不足，特别是位势高度场，整个垂直层自上而下表现一致，各层的最大频率均超过0.4，其中500 hPa位势高度场的最大频率接近0.438；对比各预报变量，发现V2对系统的改进最为显著的是700 hPa相对湿度、850 hPa纬向风和10 m纬向风，从图表中可以看到，各区间的频率分布平坦，与最优频率接近，这一结果与图8的结果一致；对其他变量，V2的分布虽依然呈现出U型分布，但整体分布形态有所缓解，频率大值区较V1均有下降，说明系统离散度不足的问题有一定程度的改善。

图8 2020年6月7日至7月7日新旧系统预报的（a）500 hPa位势高度、（b）700 hPa相对湿度、（c）850 hPa温度、（d）850 hPa纬向风、（e）2 m温度和（f）10 m纬向风集合平均均方根误差（RMSE）与集合离散度（SPD）随时间变化Fig. 8 Time series of the RMSE (root mean square error) and the ensemble mean and the ensemble spread (SPD) from June 7 to July 7, 2020: (a) 500-hPa geopotential height; (b) 700-hPa relative humidity; (c) 850-hPa temperature; (d) 850-hPa zonal wind ; (e) 2-m temperature; (f) 10-m zonal wind.blue is V1, and red is V2

图9 2020年6月7日至7月7日新旧系统预报的120 h的（a）500 hPa位势高度、（b）700 hPa相对湿度、（c）850 hPa温度、（d）850 hPa纬向风、（e）2 m温度和（f）10 m纬向风的Talagrand分布Fig. 9 Talagrand diagram for (a) 500-hPa geopotential height; (b) 700-hPa relative humidity; (c) 850-hPa temperature; (d) 850-hPa zonal wind; (e) 2-m temperature and (f) 10-m zonal wind for 96–120-h forecast period from June 7 to July 7, 2020. Blue is V1, and red is V2

3.2.3 CRPS评分

进一步从概率预报的角度来检验系统升级前后的预报能力，图10给出了各变量CRPS随时间的变化曲线。由图可见，系统升级后，整体的CRPS均呈现出明显的下降趋势，说明系统的整体预报能力有所提升。对不同的变量，预报能力各异，其改进的幅度也存在差别。具体而言，CRPS值变化幅度最大的是500 hPa的位势高度场（图10a），随着预报时效的延长，V1的CRPS呈单调递增的趋势，变化区间为0.5～2.4，V2除前24 h降低，其它时次的变化趋势与V1相似，但CRPS的绝对数值上有大约0.5的降幅。此外，改进幅度显著的还有850 hPa的温度和纬向风，36 h温度的CRPS值从1.4降低至0.6，120 h纬向风的CRPS值从1.3降低至0.65，改进幅度均在50%以上。此外，对于温度的预报，无论是大气中低层850 hPa（图10c）还是地面2 m的温度（图10e），V1的CRPS呈现波动的趋势，V2为相对平滑的曲线，这与其他变量一致，说明V2预报的连续性和一致性更好。CRPS的绝对数值大小，也反映出系统对各变量的预报准确性，V2对中低层纬向风的CRPS各时次均在0.5附近，700 hPa相对湿度和850 hPa温度的CRPS也控制在0.4～1.0范围内，说明系统对上述变量的预报能力优于500 hPa位势高度场和2 m温度，这也与前文的结论一致。

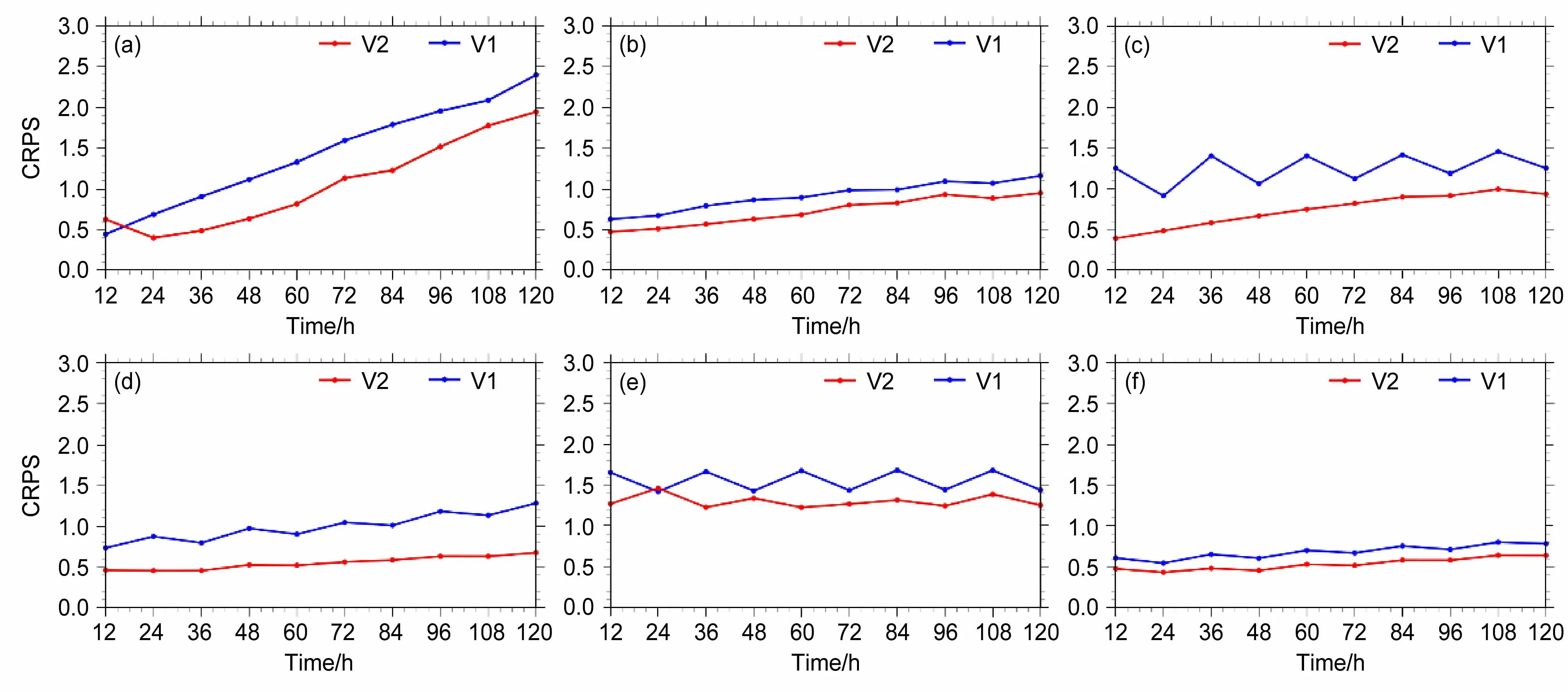
图10 同图8，为CRPSFig. 10 Same as Fig.8, but for CRPS

4 2020年6月15～16日梅雨降水

基于全国自动站资料绘制2020年6月15日00:00至16日00:00（协调世界时，下同）24 h累计降水量（图11a），关注安徽省中部和南部、江苏省南部及上海这一范围的强降水，各站累计雨量普遍在100～150 mm；从天气分析可知（图略），这次过程的环流背景为典型的江淮梅雨配置：欧亚大陆的中高纬地区，呈现两槽一脊的形势；地面天气图上，长江沿岸和四川盆地为静止锋，其中中国东部地区的静止锋与中低空切变线位置较重合，给长江下游沿岸带来持续性的暴雨。为了解华东区域中尺度集合预报系统在中后期对强降水的预报能力，分析6月13日00:00起报，系统72 h大于50 mm的降水概率预报（图11b–c）。从预报的雨带位置上看，V1的强雨带主体位于长江以北，降水中心概率约50%～70%，但相比实况的强降水落区，预报略微偏北，以致安徽中部的强雨带出现断裂，且安徽南部地区出现漏报；V2的强雨带整体组织性较好，从空间分布上看，从河南南部、安徽省中南部至上海一线均呈现出连续的降水，可以看到其中有两个强降水中心，其一位于江苏省西南部，出现暴雨的概率＞70%；另一个位于安徽省中南部、豫鄂交界地区，出现暴雨的概率更高（局部地区达到80%以上），而且与实况的强降水中心更为吻合。

图11 （a）2020年6月15日00:00至16日00:00 24 h累计降水量（单位：mm）分布；2020年6月13日00:00起报（b）V1、（c）V2系统预报大于50 mm的降水概率分布Fig. 11 (a) Distributions of 24-h accumulated precipitation (units: mm) from 0000 UTC 15 to 0000 UTC 16 June 2020, and the probability more than 50 mm of (b) V1 and (c) V2 for 96–120-h forecast period

5 小结与讨论

本文通过考虑区域模式预报中不确定性的各种来源，分别引入初始场误差、侧边界误差和模式误差来构建新一代的华东区域中尺度集合预报系统（SWARMS-ENV2），并从提高集合系统离散度的角度出发，对SPPT方案的参数进行优化；将新旧系统开展2020年为期一个月的梅雨期降水试验，得到如下结论：

（1）通过对SPPT方案中参数的敏感性试验证实了所调优的参数具备一定的通用性。对预报的影响大小依次为：格点方差、随机扰动场的去相关空间和随机扰动场的去相关时间。根据模式的自身配置，合理调整三个参数的阈值，从而强化物理过程的随机效应，通过对大气中低层的风场、湿度场的影响，可以有效地提高集合系统整体的可信度和预报能力。

（2）梅雨期降水试验的评估结果表明：升级后的华东区域中尺度集合预报系统在各时次各量级的降水TS评分均有所提升，但仍然存在着降水强度偏大的问题。

（3）综合各类降水概率预报的评估结果可见：系统升级后对中到大雨预报的准确率和可信度提升明显，对强降水事件的描述更准确。

（4）形势场的检验结果表明，SWARMSENV2各变量的分布表现出不同的特征：系统对大气中低层风场、湿度场和2 m温度的预报效果有明显改进，但对形势场的预报仍存在一定的预报偏差。相比SWARMS-ENV1，系统升级后，其整体性能明显提升，其优势可概括为：系统预报误差的降低，离散度的增加，即系统整体的预报可信度增加；从用户的角度而言，对一些关键过程，预报的可提示性增加，产品的可用度提高。