封装设计中传输线损耗的理论计算

周立彦，汤文学，庞影影，王剑峰，王 波

（中国电子科技集团公司第五十八研究所，江苏无锡 214035）

1 引言

当时钟频率低于10 MHz 时，与数字信号边沿对应的交变信号在互连中总能畅行无阻，封装仅是在实现电连通的基础上完成对电路的支撑保护。随着电子信息技术的发展，吉赫兹频率的高速应用和复杂微系统下的大尺寸电气互连使信号完整性问题无可回避。

信号的传输能量损耗主要来源于辐射、耦合到邻近导体、阻抗失配引起的反射、导体损耗以及介质损耗，传输损耗过大会引起信号失真[1-3]。单一信号网络设计中可以忽略辐射和耦合的损耗，影响信号传输质量的电气特性基本可以通过网络的阻抗特性和传输时延来描述。基于傅里叶变换，时域中任何波形可由正弦波组合完全且唯一地描述，由不同频率的正弦波分量及其幅度/相位值构成的频谱包含时域的所有信息，传输阻抗与反射的概念得以通过频域构造体现。

在传输线设计时，理想情况是保持阻抗匹配，以实现传输透明。然而微带线、带状线的阻抗计算是存在误差的[1]；平面互连的拐角、分支与回流路径的不连续将会引起阻抗不同程度的突变[4-6]；过孔、反焊盘、硅通孔（TSV）等垂直结构甚至受限于工艺规则，可能无法达到阻抗设计的要求[7-9]。由于常见的工具书并未给出关于反射的进一步数学推导，对于传输阻抗匹配的设计往往依赖于经验准则积累和仿真数据归纳。

本文从传输线理论基础出发，推导了单一低损传输网络中散射参数的数学表达式，直观展现阻抗匹配与传输时延对散射参数的影响。结合主流仿真工具，深入阐述了反射分析在频域和时域环境下的一致性和差异性，对阻抗匹配设计引起的信号完整性问题提供了优化思路。

2 单一传输网络中散射参数的推导

在传输线理论中，基于传输线的集总电路模型可以由基尔霍夫定律求解电压与电流的关系[2]：

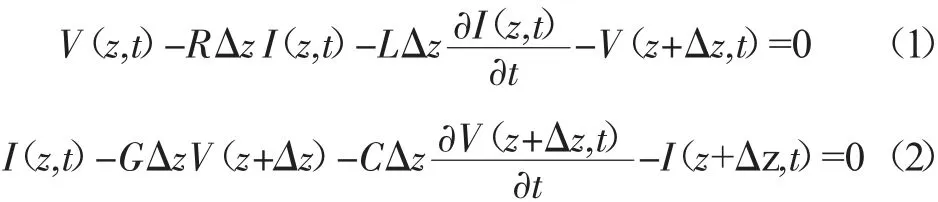
其中，z、t 分别为电路模型中的位置、时间变量；V、I 为与位置、时间相关的电压与电流；R 表示传输线单位长度的串联电阻，由传输线的有限电导率和传输截面尺寸决定，单位为Ω/m；L 表示传输线单位长度的串联电感，由导体磁导率和几何形状决定，单位为H/m；G 表示传输线导体间单位长度的并联电导，来源于传输线导体间填充材料的介电损耗，单位为S/m；C 表示传输线导体间单位长度的并联电容，由传输线导体的紧贴程度决定，单位为F/m。该模型的近似程度随着Δz→0而提高，达到分布式模型的效果，此时得到传输线方程：

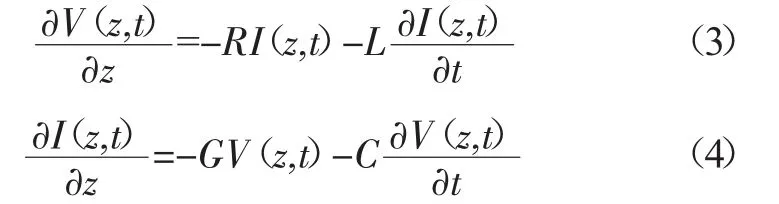
得到简谐稳态通解，仅与位置相关的电压V（z）与电流I（z）的表达式为：

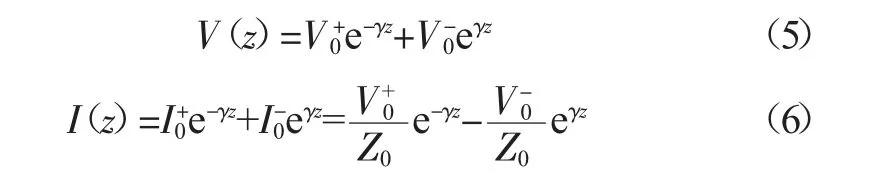
其中，V0+、V0-分别为沿坐标轴正向/负向传播的电压，I0+、I0-分别为沿坐标轴正向/负向传播的电流，复传播常数γ 为：

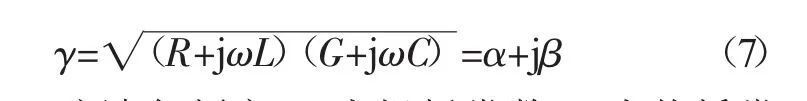
其中，ω 为正弦波角频率，α 为损耗常数，β 为传播常数，进而得到特征阻抗Z0为：

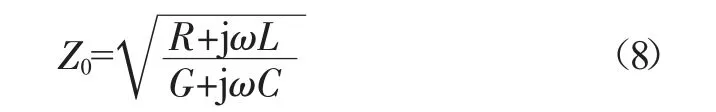
由于R、L、G、C 均为单位长度值，因此信号传输感受到的瞬时阻抗由该处传输结构截面的尺寸、材料特性决定，并且无论在时域或是频域中，阻抗总是电压与电流的比值。

在图1 的均匀传输线示例中，假定输入信号从端口1 进入，根据式（5）（6）简谐稳态通解，可以标定传输线（-l≤z＜0）：

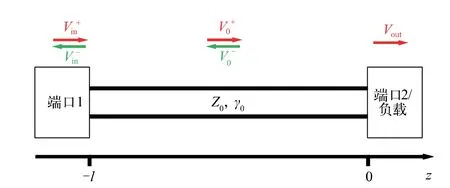
图1 长度为l、阻抗为Z0、传播常数为γ0 的传输线

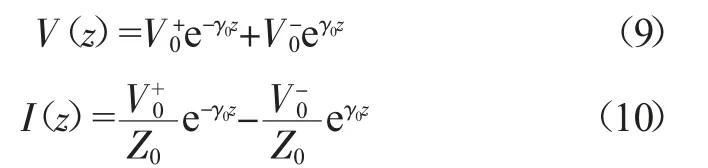
其中，γ0为-l≤z＜0 段的传输线上复传播系数。在低损情形下[1]，忽略直流电阻，R→0，G→0，R≪ωL 时，传播常数，v 为电磁波在传输结构中的传播速度；损耗常数α 包含导体损耗系数αcond与介质损耗系数αdie2 部分，其中ρ 为导体电阻率，w 为传输结构对应的导体宽度，c 为真空中的光速，Dk、Df分别为介质的相对介电常数和介电损耗角正切值，介质损耗与频率f 成正比，在高频下起主导作用；导体损耗与频率的平方根成正比，在低频下起主导作用。

输出端（z≥0）与阻抗Zp2的负载等效，无反射波，且在z坐标0 点连续，z=0 处电压、电流及相互关系为：

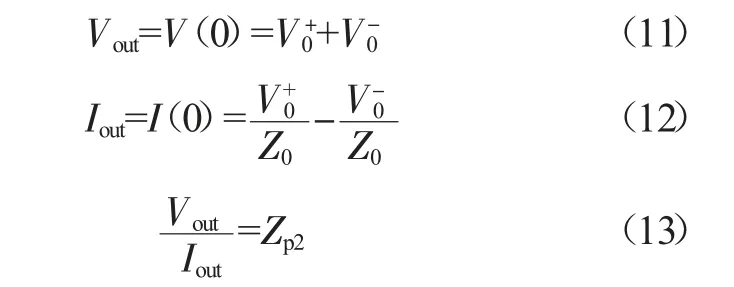
联立式（11）～（13）可解得：

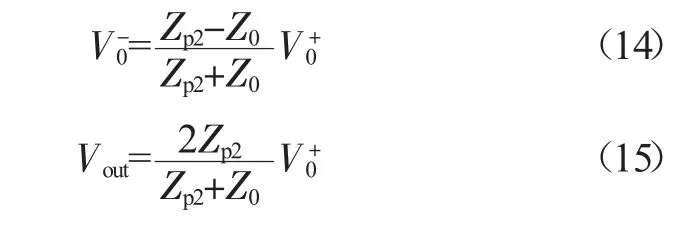
这与反射系数、透射系数的表达式一致。

根据阻抗的定义，在z=-l 处有等效输入阻抗Zin：

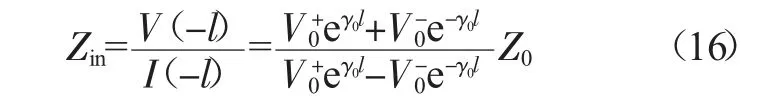
同样，在输入端（z＜-l）有：

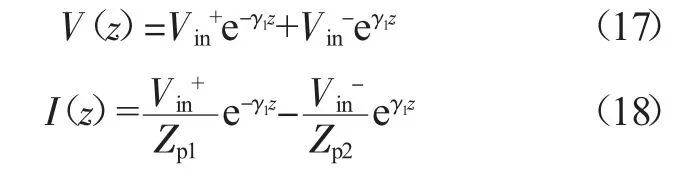
其中Vin+、Vin-分别为端口1 的输入波、反射波幅值，输入端口的等效复传播系数γ1经联立后可消除，Zp1、Zp2分别为两端口阻抗。考虑z=-l 处的连续条件，联立式（9）～（10）、（16）～（18）得到：

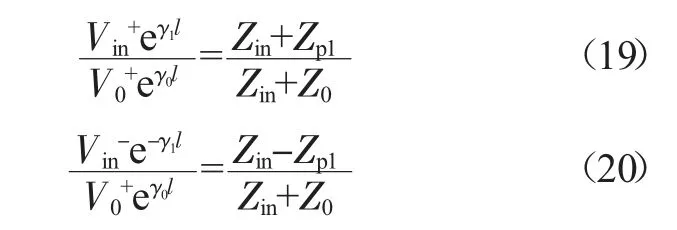
2.1 回波损耗

端口1 的回波损耗定义为反射波与入射波的电压比：

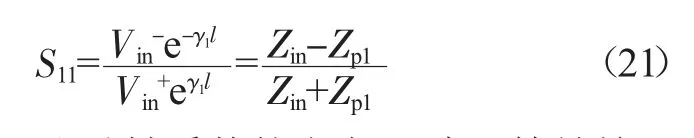
该式与z=-l 处反射系数的定义一致，等效输入阻抗Zin包含了z＞-l 所有结构的阻抗特性，进一步展开为：

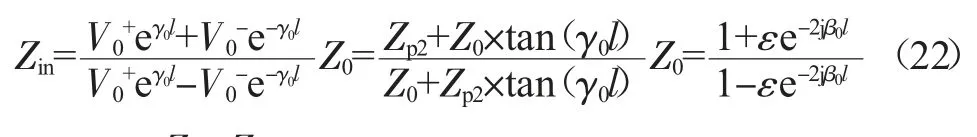
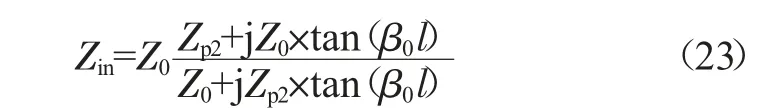
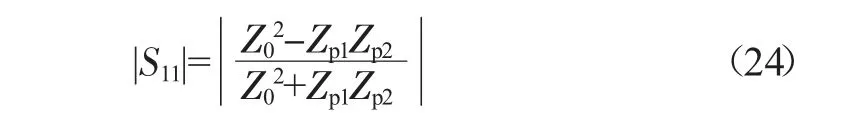
当Z0＞max（Zp1, Zp2）或Z0＜min（Zp1, Zp2），S11为反射叠加极大值，当min（Zp1,Zp2）＜Z0＜max（Zp1,Zp2），S11为反射相消极小值。

考虑2 端阻抗一致（Zp2=Zp1）的无损（α0=0）情形，由式（21）进一步展开得：

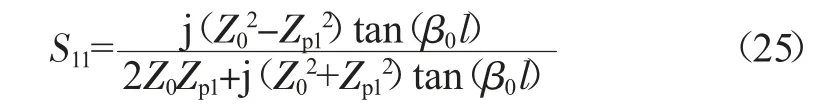
由式（25）可知，减小阻抗失配程度和减小由传输长度l决定的相位值是降低回波损耗的关键。

2.2 插入损耗

输入/输出端阻抗一致时，插入损耗定义为出射端口透射波与入射端口输入波的电压比[1]。广义上，基于能量守恒定律，S21幅值应调整为输出与输入能量比值的平方根：

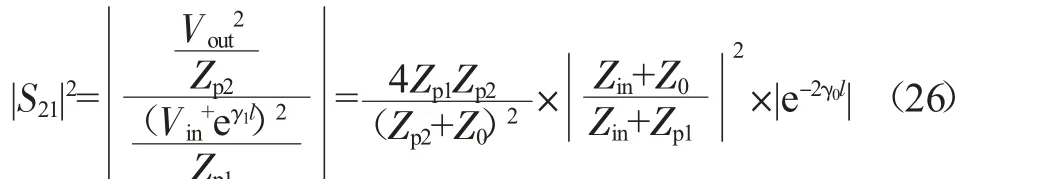
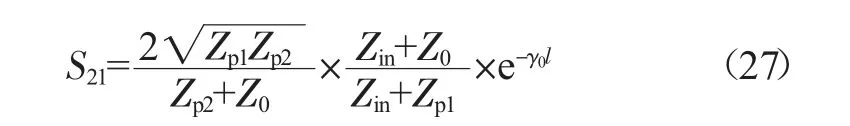
无损情形下可得

2.3 推广计算

根据单段传输线的推导结果，利用等效输入阻抗的概念，可以将S 参数的推导推广到n 段阻抗突变的有损传输线（图2）计算中，从第n 段传输线起点看向输出端/负载的等效输入阻抗Zin（n）为：

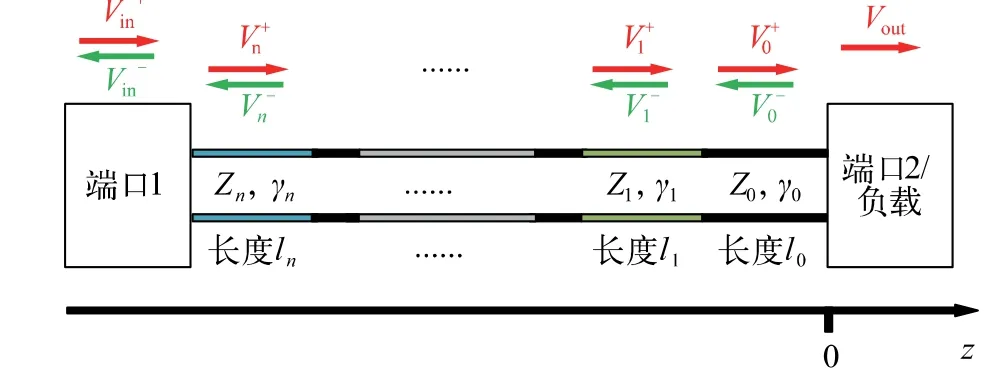
图2 包含多段阻抗突变的传输线计算用模型

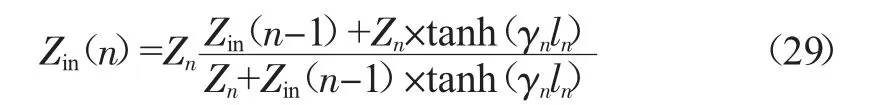
其中，Zn为第n 段传输线特征阻抗，γn为该段传输线复传播常数，ln为对应长度，初始段输入阻抗：

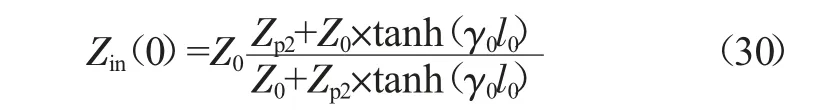
得到端口1 处的回波损耗为：

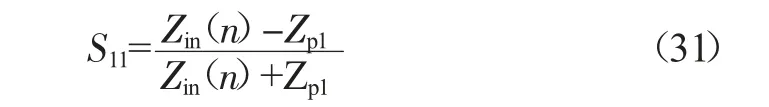
同理，插入损耗推广为：

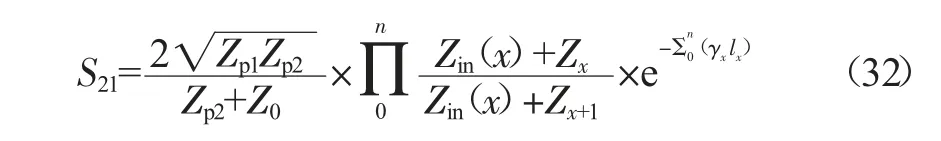
通过计算工具仍可证明单一无损传输结构中的能量守恒|S11|2+|S21|2=1。为进一步验证该计算的适用性，采用Ansys 的高频电磁场仿真工具HFSS 对典型传输结构进行建模仿真，并与本文的推广公式计算结果进行对比。考虑目标特征阻抗50 Ω 的带状线结构，其中，线长为20 mm，线宽为100 μm，金属铜厚度为15 μm，上下层介质厚度为300 μm，介质参照某型号低温共烧陶瓷材料（相对介电常数Dk=5.8，介电损耗角正切值Df=0.002），根据仿真分析，该模型阻抗分布接近于过孔（57 Ω）-走线（49 Ω）-过孔（57 Ω）的3 段结构，S 参数仿真结果与计算值对比如图3 所示。本文中的损耗计算适用于以铜等高导电材料为导体的低损情形，插入损耗的差异主要来源于窄线宽情形下侧边趋肤效应修正导体损耗系数。进一步的拟合还需结合低频串联电阻及高频慢波特性影响下的回路电阻，暂不做展开。

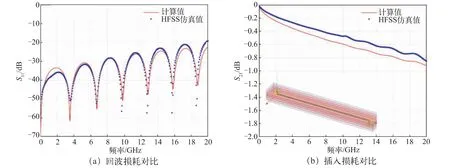
图3 带状线HFSS 仿真结果与计算值对比

3 基于散射参数的时域计算

时域周期波形可由正弦波组合完全且唯一地描述，时域波形U(t)经傅里叶指数展开表达为：

其中ω0为周期波形的角频率，傅里叶系数F（nω0）的计算为：

其中，T 为U（t）的信号周期，由此，时域周期波形可拆分为倍频幅值为对应傅里叶系数的弦波，根据频域插入损耗的定义，很容易得出结论，经过一段传输结构后，输出波形为衰减后倍频弦波分量的叠加：

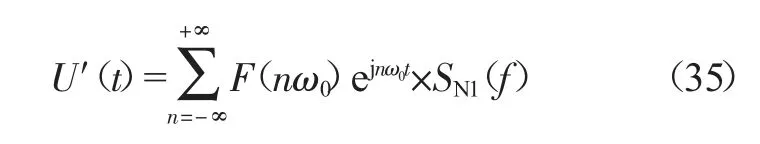
其中，SN1（f）为对应频率下端口N 的散射参数。

值得注意的是，时域中对实信号的处理只保留实部而省略虚部信息。对于频域计算来说，动量与能量的本征函数应是同时包含实部与虚部的复信号形式，脱离复信号的计算无法考虑弦波的相位信息，往往是违背能量守恒定律的。时域信号可由倍频分量通过频域计算转换，因此，透射系数/反射系数在时域/频域的定义一致。多数工具书中推荐采用反弹图计算信号在阻抗不连续路径中多次反射后的波形，推导可证形成收敛级数叠加，并与基于散射参数的转换计算结果一致，此处不做展开。

4 分析与讨论

4.1 回波损耗高频恶化因素

在工程分析中，回波损耗似乎总是随着频率升高而恶化。这种结论需要分2 种情形来讨论：一是分析频段较短的情形，二是在较长频段范围内不可忽略短突变影响的情形。

短频段内：默认测试/仿真条件下2 端阻抗一致，由式（25）得到均一传输结构的回波损耗在对应1/4 波长频点处为极大值，即在范围内回波损耗单调增大，以长度15 mm 的走线为例，在Dk=4 的介质中回波损耗单调上升的范围为0～2.5 GHz。

长频段内：该单一均匀传输结构回波损耗在2.5 GHz后呈周期性特征，其无损情形如图4（a）所示，其中，设置传输线特征阻抗为70 Ω 以突出变化，在波长对应的2.5 GHz、7.5 GHz 等频点回波损耗有极大值，约为-9.8 dB；在考虑损耗时，回波损耗曲线呈阻尼衰减，曲线如图4（b）所示。

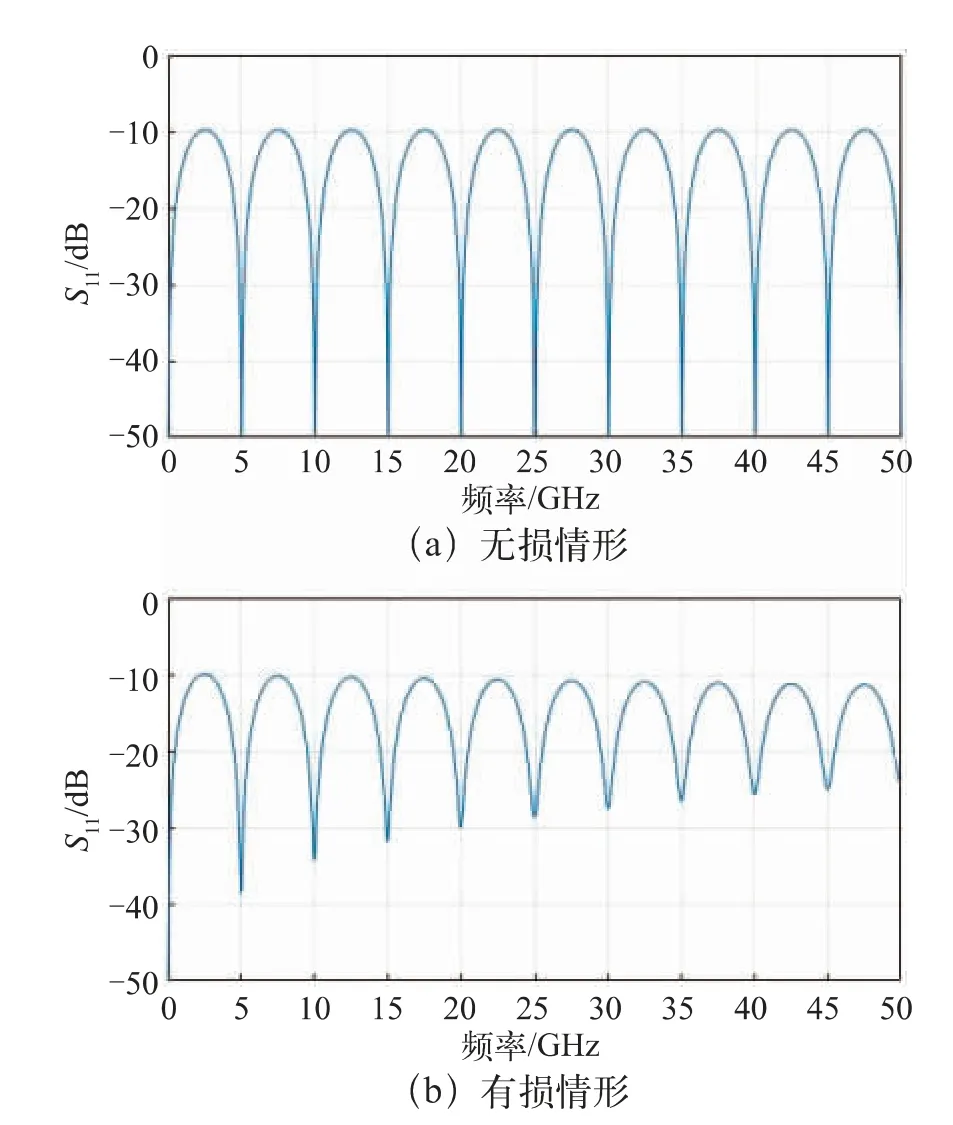
图4 均一传输结构在无损和有损情形下回波损耗的区别

考虑存在多段阻抗不连续的情形，在长度为15mm、阻抗为70 Ω 的传输线后增加一段长度为3 mm、阻抗为100 Ω 的传输线，其无损情形下回波损耗如图5（a）所示。图5（b）为长度为3 mm、阻抗为100 Ω 的传输线回波损耗，其1/4 波长频点12.5 GHz 处对应回波损耗极大值为-4.4 dB。可发现，图5（a）中回波损耗曲线呈现2 段传输线各自回波损耗的“叠加”状态，由于3 mm传输线阻抗失配程度更大，在0～25 GHz 范围的大周期和回波损耗极值由这段较短传输线决定，阻抗失配程度较小的传输线在回波损耗曲线局部仍保留部分的周期性特征。可预见的是，在有损情形下，随着频率提高、损耗增大，阻抗失配程度较小的传输结构引起的局部周期性特征将会进一步被消除，从而在由阻抗失配最恶劣段决定的半周期中呈现上升趋势。实际情形中，这些难以控制的阻抗突变端往往由一些转换用的垂直结构造成，例如过孔、焊盘、焊球等。

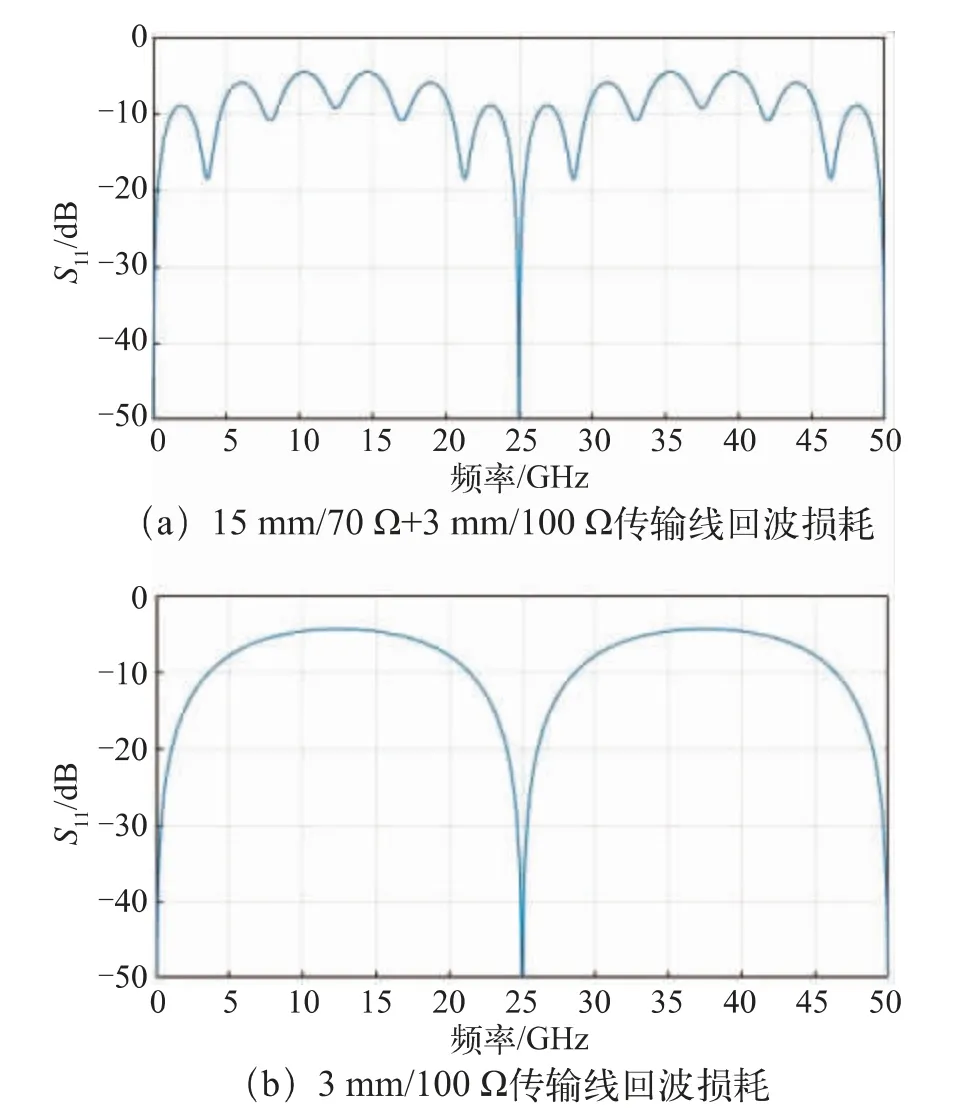
图5 有无3 mm/100 Ω 传输线对回波损耗的影响

4.2 传输结构对称性对回波损耗的影响

借助计算工具可以验证，对于多段阻抗突变传输结构的插入损耗，S11=S22总是成立，这是由无源网络的互易性决定的。值得注意的是，非对称的传输结构下，往往导致S11≠S22。进一步地，在无损情形下，传输结构在阻抗、长度上的分布不对称，并不会导致2 端回波损耗曲线的差异，2 者的差异如图6 所示。

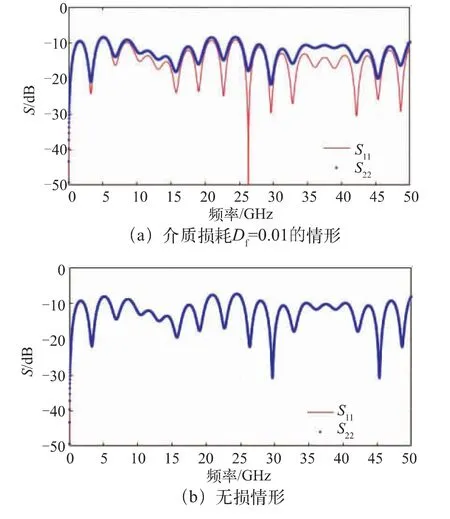
图6 3 段阻抗分布为3 mm/60 Ω、15 mm/70 Ω、5 mm/80 Ω的传输结构在2 端口50 Ω 下回波损耗S11、S22 的计算差异

为探究阻抗失配分布位置对S 参数的影响，考虑将1 段1.5 mm/75 Ω 的突变接入特征阻抗55 Ω 的传输结构中，总长度为20 mm，Dk=4。根据推算，1.5 mm对应的回波损耗周期为50 GHz。图7 中，当该段突变处于传输线的不同位置时，在较宽频段范围内其回波损耗曲线趋势与1.5 mm 对应回波损耗贴合。尽管不同的突变位置会导致不同阶段反射波的相位差异，但该差异性在考虑损耗的情形下进一步被缩小。阻抗的分布定位可以通过时域反射计（TDR）做进一步测算，但阻抗失配程度与对应的时延才是决定S 参数质量的关键。

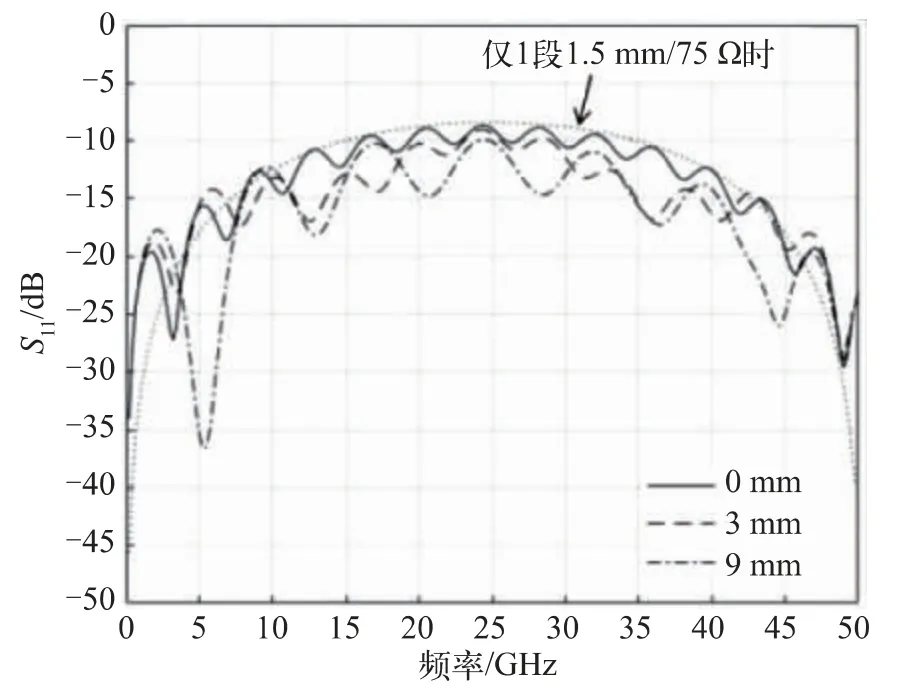
图7 1.5 mm/75 Ω 的1 段突变距离端口1 分别为0 mm、3 mm、9 mm 时对回波损耗的影响

4.3 阻抗匹配设计结果预测

实际封装/PCB 的工程设计中，往往只能保证均匀走线部分实现与端口的阻抗匹配，走线的拐角、跨平面，甚至难以控制阻抗的过孔、焊盘、焊球等结构，无可避免地会引入不同程度的阻抗失配，当回波损耗恶化到一定程度，会对插入损耗造成明显影响，从而导致传输结构的“透明度”下降。为应对存在特殊走线或工艺容差的情形，设计人员应对S 参数的浮动有所掌握。图8 为在无损情形下，基于式（25）所得回波损耗与传输结构阻抗失配百分比及相位β0l/2π 的数值分布关系，在低速情形/较短传输长度/低阻抗失配时，可以忽略因反射造成的损耗。

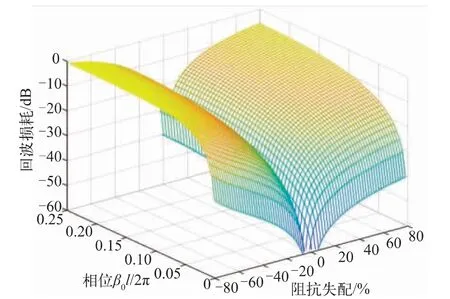
图8 无损情形下，回波损耗、β0l/2π、阻抗失配百分比的关系

射频、高速数字类互连设计中，为达到透明传输，通常要求回波损耗在工作频段内低于-15 dB 甚至-20 dB。根据计算，当传输线阻抗偏差在-9.5%～+10.5%时，回波损耗峰值总在-20 dB 以下。过孔等难控的阻抗不连续会造成整体传输进一步恶化，以-20 dB 为衡量标准，表1 为在对应工作频率下可允许的阻抗失配长度。

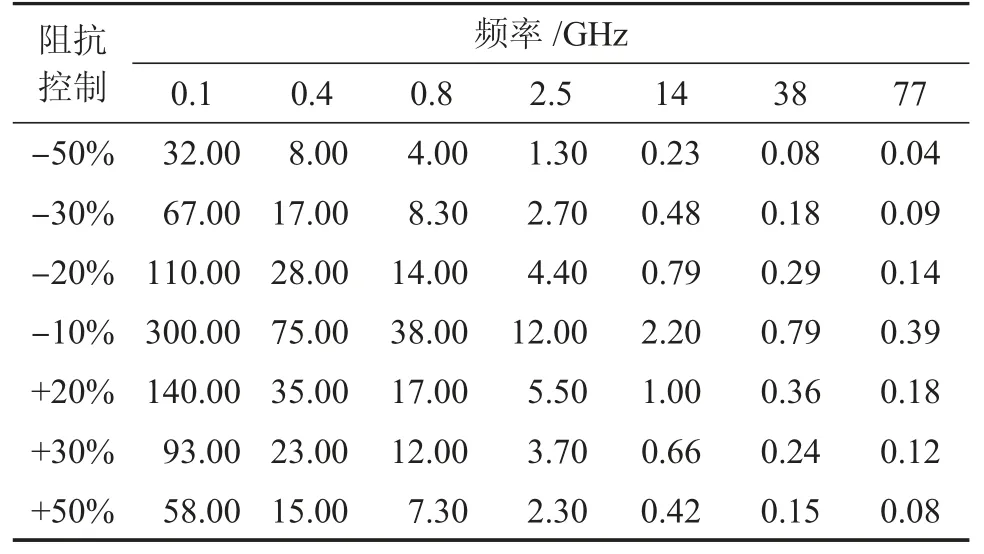
表1 不同阻抗匹配情形、特定工作频率下，满足传输回波损耗小于-20 dB 的最大走线长度单位：mm

当阻抗匹配时，由反射造成的能量损耗忽略不计，此时传输结构的插入损耗可由互连长度及工作频率进行估算。图9 为在PCB 板材（Dk=4.4，Df=0.02）中，传输结构插入损耗与传输长度及频率的数值分布关系图。

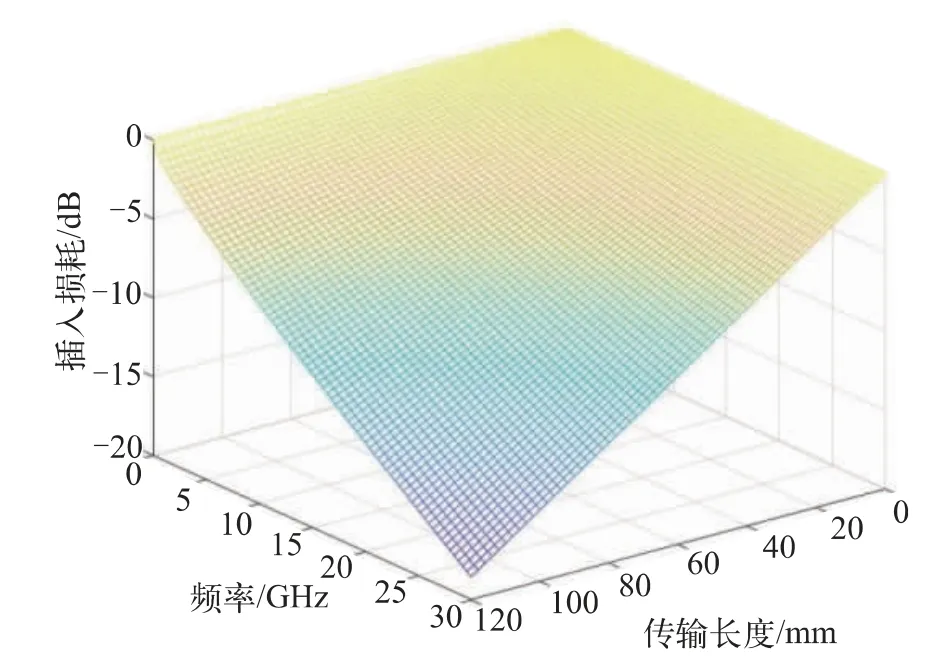
图9 无反射情形下，插入损耗、传输长度、频率的关系

某些设计的引出端尺寸节距往往囿于下一级封装，导致阻抗不连续。通常反焊盘设计可以有效抵消焊盘处容性效应导致的阻抗骤降，但无法同时兼顾对过孔阻抗的影响，因此整体的阻抗匹配设计不可一概而论。某些情形下反常规的阻抗调控却可以得到更优的传输结果，这种现象可以通过阻抗分布计算理解。在模拟3 段阻抗分布为平面走线（10 mm/90 Ω）-垂直过孔（0.8 mm/80 Ω）-焊盘焊球（0.8 mm/50 Ω）的传输结构中，过孔的阻抗调节更为灵活，区别于匹配100 Ω的常规思路，当过孔段阻抗进一步提高到130 Ω 时，0～10 GHz 范围内的S11得到进一步优化，如图10 所示。

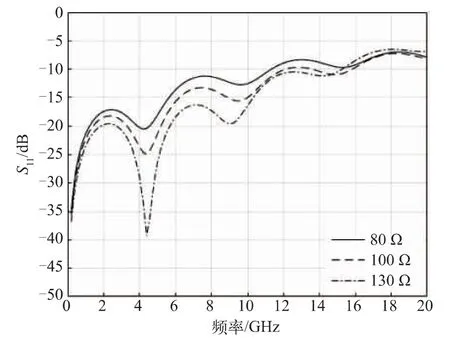
图10 3 段阻抗的传输结构中，反常规调整中间段对S11 的影响

5 结束语

本文基于传输线理论，对单一网络中的阻抗匹配原理进行了推导计算，得到了散射参数关于阻抗失配程度和分布长度的直观数学表达式。借助等效阻抗的概念可以将散射参数的计算由单一均匀网络推广到多段阻抗分布的传输线结构中，并进一步探讨了反射在频域和时域中计算的一致性和差异性。本文的计算符合能量守恒定律，与主流仿真工具的结果对比也取得了较好的验证结果。文章同时提供了几种频域分析中常见现象的解释。本文的结论可以帮助初涉信号完整性领域的人员深入浅出地理解阻抗匹配设计的重要性，为高速、高频设计中的问题排查和快速优化提供思路。