基于深度学习的地震速度谱自动拾取研究

2022-12-03崔家豪杨平王洪强边策胡扬潘海侠

地球物理学报 2022年12期

崔家豪，杨平，王洪强，边策，胡扬，潘海侠*

1 北京航空航天大学软件学院，北京 100191 2 中国石油天然气集团东方地球物理勘探有限责任公司，河北涿州 072750

0 引言

叠加速度分析是常规地震数据处理中的重要环节之一，也是层析反演、叠前偏移、阻抗反演和全波形反演等初始速度模型建立的基础（潘宏勋等，2008；Taner and Koehler，2012）.由于拾取叠加速度需要考虑地震噪声、多次波、绕射波和构造复杂性等诸多因素的影响（戴晓峰等，2020），因此拾取工作需要具有丰富地震处理经验和地质学术背景的人员来完成.随着石油勘探技术的不断进步，地震数据的规模和复杂性在近些年来一直在不断增长，而传统人工能量团识别与叠加速度拾取的工作模式容易受拾取标准不一致及人为因素干扰而产生误差，难以满足实际生产过程中对拾取精度和效率的要求.如何从速度谱中自动拾取叠加速度成为该行业面临的挑战之一.当前速度谱自动拾取的方法主要包括优化搜索方法和机器学习方法.

基于优化搜索的方法是在层速度约束条件下，采用迭代或搜索算法寻找地质上合理的速度模型.算法以层速度作为初始模型，通过反演的方式来得到最优的速度模型.Toldi（1989）最先提出基于速度谱中叠加能量的自动速度拾取方法.Zhang（1991）将Viterbi算子引入到地震资料处理中并解决了关于拾取的一些问题，林年添等（2013）对该方法进行了改进，将用于图像处理的光顺技术引用到速度谱能量团曲面的处理环节，借以提高速度谱的分辨率，然后再通过Viterbi算法自动搜索及获取最优解.Lumley（1997）和陈志德等（2002）提出了一种利用蒙特卡洛方法对初始速度加以随机扰动来自动拾取层速度.Almarzoug和Ahmed（2012）将速度拾取视为变分问题，通过有限差分法求解最优拾取轨迹.Leite和Vieira（2019）将非线性优化方法应用于速度拾取中，在满足边界条件的前提下设置合理的搜索带宽，然后运行非线性函数智能拾取.Li和Biondi（2009）以及Oliveira等（2013）分别将模拟退火算法和遗传算法应用于速度拾取中.这些方法在获取相对简单地质体的速度时已经取得了一定的效果，但是对于横向速度突变的地区拾取准确性相对不高，且需要过多设置算法超参数、初始化模型，这并不能实现完全的自动取速过程.

基于机器学习的方法是通过学习速度谱中能量团的特征来获取叠加速度.在近期的研究中，Huang和Yang（2015）采用Hopfield神经网络（Hopfield Neural Network,HNN）对速度谱图像中的速度进行自动拾取.Smith（2017）和Song等（2018）将基于无监督学习的聚类分析技术应用于速度谱自动拾取过程中.该方法依据不同的属性将速度谱划分为若干个类别，每个类别中的数据具有一些共同的特征，通常根据某种距离度量进行分组，然后将聚类中心映射为正确的“时间-速度”对.K-means聚类是最常用的聚类方法之一（Hung et al.，2013；Ahmad and Hashmi，2016），该算法使用欧几里得距离度量将每个数据点分配到最近的聚类中心.对于每个聚类中心，计算分配给它的所有数据点的平均值，这个平均值成为聚类中心的新位置，每个聚类的聚类中心即为我们所要拾取的叠加速度点.然而传统的K-means聚类方法容易受到离群点的影响，使得聚类中心偏离主要数据区域.Liu等（2018）提出了一种相似加权K-means聚类的新方法，该方法对不同信噪比的数据点赋予不同的权值，使聚类中心更接近权重大的数据点.由于不同速度谱所需拾取的能量团个数不一致，Chen和Schuster（2018）以及王迪等（2021）新提出了一种自底向上的策略来实现K-means迭代过程，该方法可以逐步迭代找到聚类类别最少的聚类分布.除此之外，加速聚类算法（Zhang and Lu，2016）以及DBSCAN聚类（Schubert et al.，2017；Bin Waheed et al.，2019）也被应用于智能速度谱解释过程中.然而传统机器学习方法也存在一些问题，如易受到噪声和离群点影响，部分拾取点偏离主要数据区域，进而影响到速度拾取精度.近年来，随着计算机性能的提高，应用深度学习方法拾取叠加速度的研究越来越多.Ma等（2018）以及Biswas（2018）和Fabien-Ouellet等（2020）分别采用卷积神经网络（Convolutional Neural Network,CNN）和循环神经网络（Recurrent Neural Network,RNN）来拾取速度谱中的叠加速度.在信噪比较高的工区中，以上深度学习方法可以提高叠加速度的拾取精度，但对于信噪比低的工区，速度拾取的准确性不足且受到噪声的干扰比较大.

为了有效解决速度拾取准确率不高的问题，本文提出了一种深度学习的方法.该方法将速度谱视为图像进行处理，结合目标任务特点改进了基于卷积神经网络的FCOS目标检测模型（Tian et al.，2019）用于速度谱中叠加速度的自动拾取.与传统的目标检测网络不同，改进后的FCOS检测器具有以下优点：①显著减少了设计参数的数目，一方面提升了对能量团检测的识别效果，同时构建的混合损失函数增强了模型对能量团检测的敏感度，使得能量团识别和叠加速度拾取仅通过深度学习模型即可完成，保证了识别和拾取处理结果的一致性.②由于预测目标为叠加速度点，每个点在速度谱上的边界框具有固定的大小，使用改进后的FCOS可直接对边界框进行回归，从而避免了复杂的计算，极大地减小了内存占用并使得训练速度更快.

另外，当地震资料受多次波干扰较强时，除去一次波反射能量团以外，多次波也能形成能量团，尤其当多次波与一次波速度相差较大时，速度谱能量团聚焦特征变差，在同一时刻出现多个能量团.由于能量团较为分散，改进后的FCOS模型只能够拾取到近地表浅层的叠加速度，对于地下深层区间的叠加速度仅通过单一的FCOS模型未能有效识别，因此在处理低信噪比探区时本文在FCOS后又加入基于深度神经网络（DNN）的线性回归模型以拟合出全局速度曲线.我们从方法原理及模型训练与测试等角度阐述了本文方法的操作流程，并应用Ma等（2018）提出的传统的CNN方法与本文方法处理相同的数据集来对比验证本文方法的有效性.模型和实际地震数据的测试结果表明该网络模型准确度较高，模型鲁棒性强，能够较好的实现对复杂工区的速度谱中叠加速度的自动拾取.

1 方法原理

1.1 模型整体结构设计

结合目标任务特点设计的满足上述需求的网络模型的整体设计流程如图1所示.该模型分为卷积神经网络和线性回归网络两部分.首先对包含速度谱图像及其标签数据的数据集进行处理使其满足网络的输入要求，然后将标签数据集输入到基于CNN的FCOS模型中提取能量团的特征并计算能量团的位置.该模型能够对提取到的多尺度特征进行融合，从而提升能量团检测精度.卷积神经网络阶段输出的中间结果为预测的“时间-速度”对序列.受多次波及噪声等影响，速度谱图像中存在信噪比较低且能量团不够聚焦的区域，在该区域FCOS模型只能完成浅层区域内叠加速度的自动拾取.针对这一情况我们引入人工判别机制，当预测结果满足拾取要求时，可直接输出中间结果为最终的智能拾取结果；当预测结果不能满足拾取要求时，需要加入基于DNN的线性回归模型来拟合出能量团聚焦特性较差区域的速度曲线.本章2、3小节分别对FCOS和线性回归网络展开详细介绍.

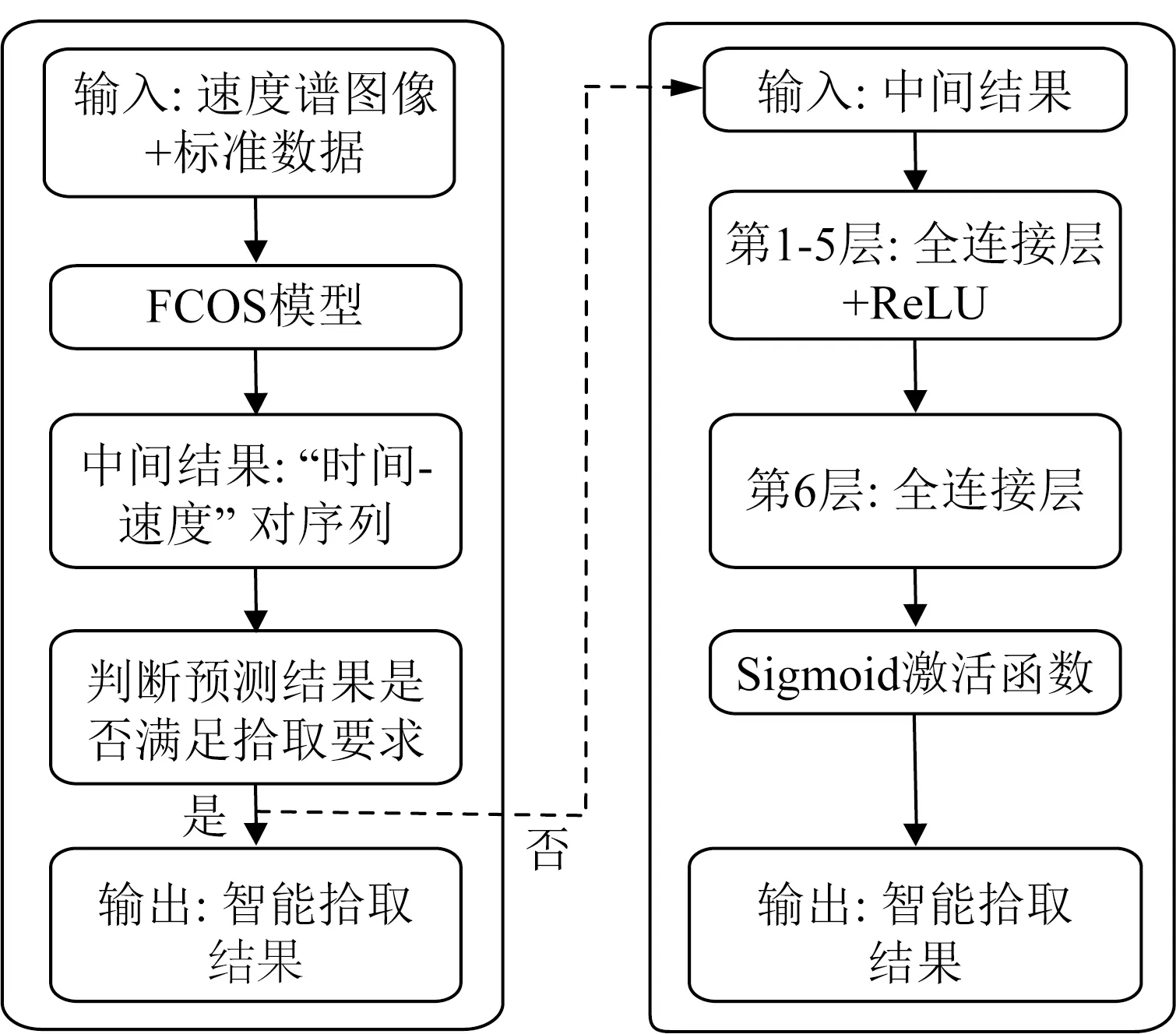
图1 模型整体设计流程图Fig.1 Overall design flow chart of the model

1.2 FCOS网络结构与工作原理

本文针对能量团结构复杂、体积小，在速度谱中难以检测等难点对FCOS网络进行了改进，改进后的模型更适用于识别和定位速度谱中能量团的位置.如图2所示，首先通过一个卷积层和一个最大池化层将原始图片转化为特征图.卷积操作（Convolution）采用卷积核提取能量团的特征，该操作能突破传统机器学习方法的限制，通过共享多个卷积核的权值，来学习每张速度谱图片的局部信息，并用于构建抽象特征图谱.卷积核共享特性大大降低了训练网络所需的参数量.最大池化操作（Maxpooling）将卷积处理后生成的特征图划分为若干个矩形区域，对每个子区域输出最大值，从而有效的压缩数据空间的大小，避免在模型训练过程中出现过拟合.然后将最大池化操作产生的特征图输入到4级降采样（Down-sample）模块中，每一级包含有若干个降采样过程，用于逐级提取数据特征.降采样模块的设计可以降低特征的维度并保留有效信息，一定程度上减少了计算量，有效解决了传统CNN网络随层数的加深容易出现的梯度爆炸或梯度消失等问题.选用1×1大小的卷积核对第4级降采样模块输出的特征图进行卷积操作，得到P5特征层.然后使用步长为2大小为3×3的卷积核对P5特征层进行两次降采样得到P6、P7特征层.同时对P5特征层进行两次上采样（Up-sample），上采样阶段通过转置卷积操作（Deconvolution）来提升特征图的大小.分别将上采样后得到的高层特征与对应的残差网络模块相同放大倍数的低层特征进行融合（Concatenate）得到P3、P4特征层，融合操作可将低层次的细节信息与高层次的语义信息结合到一起，从而使特征提取更完备.通过上述操作可在5个不同尺寸的特征层上进行目标检测，从而实现对较小目标与多尺度目标的准确识别.本文中卷积层和上采样层均采用ReLU非线性激活函数，并在卷积阶段对图像的边缘进行填充，使边缘信息提取更加充分.

图2 FCOS结构图左侧降采样模块用于逐层提取特征；中间部分进行多尺度特征融合；右侧是多个共享权重的FCOS检测头.参数含义：通道数Channel和降采样率Down-sample Rate（标注于每层左侧），H×W×C表示图像的高×宽×通道数.Fig.2 FCOS structure diagramThe left Up-sample module is used to extract features layer by layer;Multi-scale feature fusion was performed in the middle part;On the right are multiple FCOS detection heads with shared weights.Parameter meaning:Channel number and Down-sample Rate （marked on the left of each layer）.H×W×C represents the height × width × number of channels of the image.

FCOS的检测模块总体分为类别判断分支（Classification）与位置回归分支（Regression），它作用在特征融合后的多个不同层级的特征图上，同时这些检测模块的权值共享.模型的损失函数如（1）式展示：

（1）

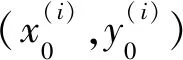
（2）

（3）

整体损失函数由类别损失Lcls与位置损失Lreg组成.对于类别损失，采用交叉熵损失（focal loss）的设计，其含义为目标与预测值之间概率分布的距离，交叉熵越小，概率分布越接近.它能够较好地解决样本不均衡问题.对于位置损失，采用交并比损失（IOU loss）的设计，其含义为预测框与标注框的交集与并集的比值，它能够编码空间相关性信息辅助更加准确地定位.

1.3 线性回归网络结构与工作原理

在不考虑速度倒转的情况下叠加速度会随着时间的增大而增大，在处理能量团聚焦特性较差的速度谱时，经验较为丰富的专家一般会根据拾取到的浅层叠加速度的线性趋势来完成对较深地层中叠加速度的拾取.而仅仅依靠单个目标检测网络很难处理复杂地质体条件下的能量团识别问题.为了完善本文的算法方案，我们在FCOS模型的基础上设计了一个线性回归网络，其本质为深度神经网络（DNN）模型.该网络主要由输入层、隐藏层和输出层等层级结构组成（图3），可通过学习浅层区域内叠加速度的线性趋势来完成对较深地层中叠加速度的预测.网络的输入为FCOS模型自动拾取的“时间-速度”对，隐藏层由若干个全连接层构成，全连接层的作用为拟合经插值处理后形成的全局速度曲线，其前向计算公式为

（4）

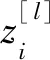
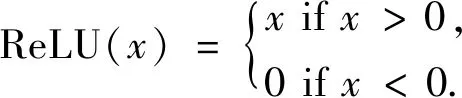
（5）

使用ReLU激活函数可以克服训练过程中出现的梯度消失等问题，加快训练速度.损失函数采用l2Loss，其形式如下：

Loss（z[l],y）=0.5×（z[l]-y）2，

（6）

式中y表示网络的输入值，z[l]表示第l层输出的数值矩阵.全连接层的反向传播过程如下：

dx=∂Loss/∂u，

（7）

其中u表示任意变量，包括z,x,W,b等.通过一系列前向和反向传播过程来不断更新网络模型的参数，直到Loss层的梯度保持平稳不再下降.网络最后一层采用sigmoid激活函数进行二分类任务，使输出转换为0～1之间的概率分布，公式表示如下：

（8）

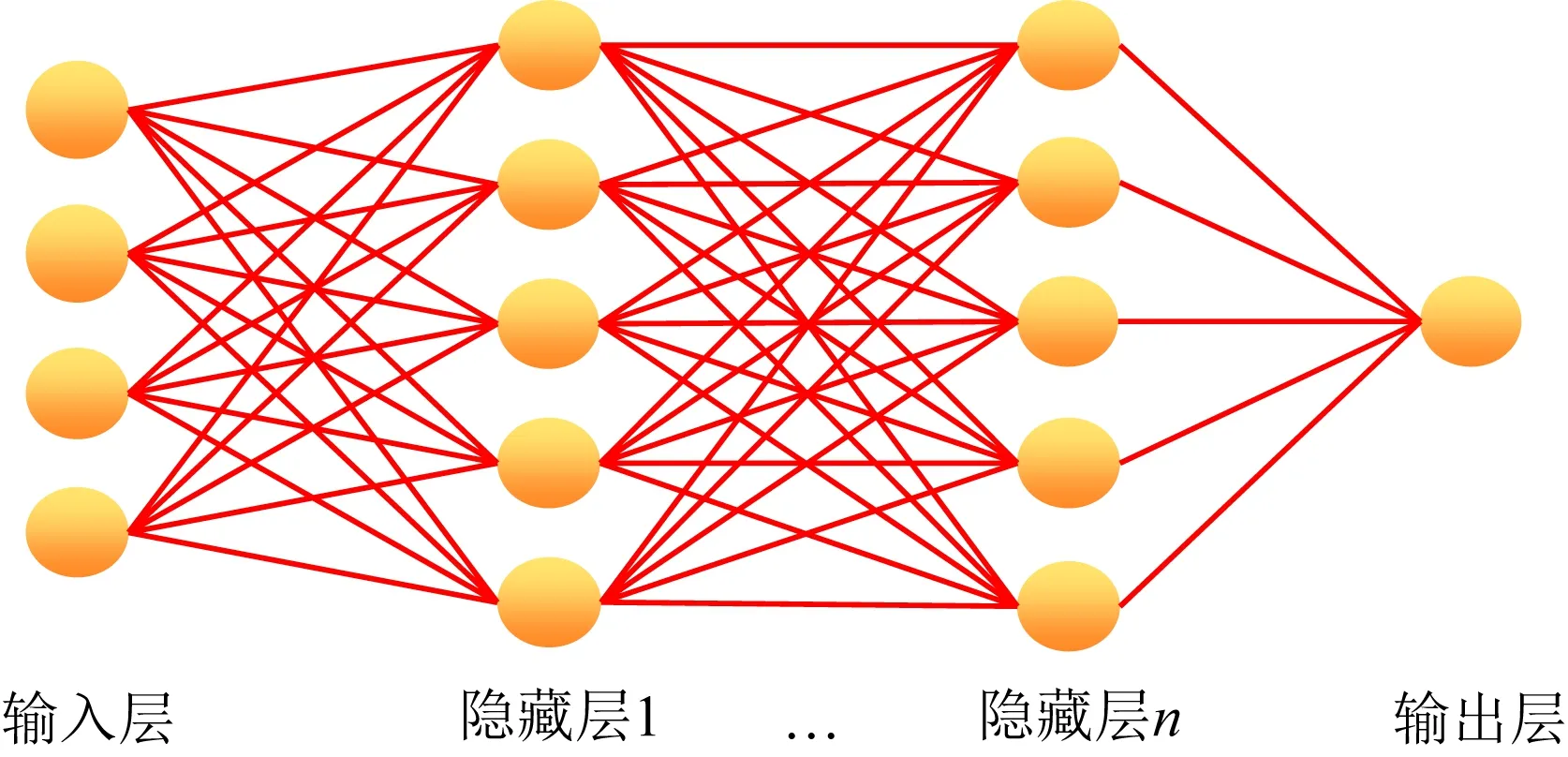
图3 线性回归网络结构图Fig.3 Linear fitting network structure diagram

2 实验与结果分析

为了验证提出方法的可行性，采用Marmousi模型数据和两个实际探区数据对本文方法进行测试.在训练阶段采用小批量梯度下降法，我们设置batchsize为2，其含义为进行一次训练所抓取的数据集样本数量.训练过程中以一个batchsize为最小结构单元进行损失函数计算和参数梯度更新，并采用双线程计算以提升程序的运行效率.实验选取Adam算法来解决参数更新过程中的优化问题，基础学习率设置为0.01，共计训练24个轮次，分别在第8轮和第11轮进行学习率衰减，权重衰减系数设置为0.0001.实验应用Pytorch深度学习框架，并使用GPU来加速训练过程.

本文使用平均准确度均值（mAP）来评估目标检测器的有效性，mAP的计算方法如公式（9）—（10）所示：

（9）

（10）

其中P表示精准度，其含义为所有预测为正样本的样本中正样本所占比例；R表示召回率，其含义为正样本被预测正确的比例.TP表示既是正样本又被预测为正样本的个数；FP表示负样本被预测为正样本的个数；FN表示正样本被预测为负样本的个数.精准度和召回率始终处于矛盾的状态，当其中一个增高，必然意味着另一个降低.以PR为横纵坐标建立坐标系，AP（Average Precision）计算方法为PR曲线下覆盖的面积，所有类别的AP进行平均，得到的即为mAP （mean Average Precision）.对于目标检测器的评估方法，其mAP越高，检测方法越有效.

2.1 模型数据

首先应用二维的Marmousi模型对本文方法进行测试，从该模型中等间隔抽取了900道作为本次测试的真实层速度场（图4）.选用主频为35 Hz的雷克子波通过声波波动方程有限差分法对该速度模型正演得到一系列CMP道集，然后对CMP道集进行速度扫描，共计算得到900张速度谱图像.再经由专家来人工拾取速度谱中的叠加速度，并从某商业软件中导出统一大小的速度谱图像及其对应的叠加速度做为标签数据.将数据集按8∶1∶1分为训练集、验证集和测试集三部分，用于训练速度谱识别模型并对该方法进行检验.在训练阶段使用梯度反向传播的方法来不断地更新优化Loss函数，并使用mAP来衡量检测模型在验证集上精度表现的优劣，实验结果如图5所示.

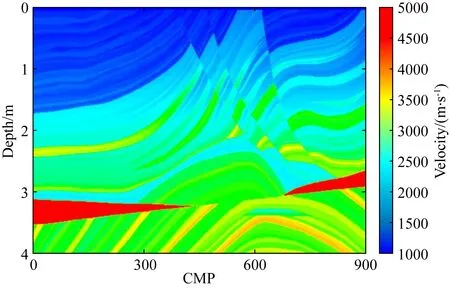
图4 层速度场模型Fig.4 Interval velocity model

从图5中可以看出通过梯度反向传播的方式来不断地更新和优化Loss后，本文方法相较传统CNN方法得到的Loss曲线更为收敛，且应用本文方法训练的目标检测器在Marmousi数据集上的mAP精度最高为74.1，而传统CNN方法在Marmousi数据集上的mAP精度最高仅为54.5.上述结果验证了本文方法在速度谱能量团检测上的有效性.

选择训练好的FCOS模型对测试集中的速度谱图片进行预测.图6（a,b）分别展示了应用传统CNN方法及本文方法拾取的叠加速度和真实均方根速度的对比.从图中可以看出在浅层区间不存在多次波的干扰，能量团集中在一个较窄的速度范围内，聚焦较好.而在2.5 s以后多次波干扰较大，多次波速度与一次波速度叠加在一起导致能量团逐渐发散，在同一时刻出现多个能量团.受深层多次波干扰的影响，传统CNN方法（图6a）仅能拾取到0.4～3.0 s时间范围内的速度，且该方法在2.3～3.0 s区间内拾取结果远偏离真实值；而FCOS方法（图6b）得到的速度曲线与真实值非常近似，证明该方法能够有效避免多次波的影响，使拾取结果具有更高的精度.图6（c—f）分别展示了Marmousi模型中第400道动校正前后的CMP道集，从动校正后的道集中可以看出，FCOS方法（图6e）拾取的速度拉平了浅层的同相轴，而深层区间受多次波剩余时差较大影响，导致同相轴随偏移距增大具有下拉现象；而传统CNN方法（图6d）在2.3～3.0 s区间选取比叠加速度小的多次波速度进行动校正，导致同相轴被错误的拉平.将FCOS方法得到的动校正后道集与真实速度动校正后道集（图6f）进行对比后发现二者主要反射同相轴拉平程度相一致，也验证了本文算法的有效性.

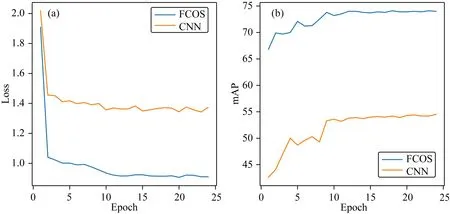
图5 Marmousi模型Loss曲线图（a）及mAP曲线图（b）Fig.5 Marmousi model loss curve （a） and mAP curve （b）

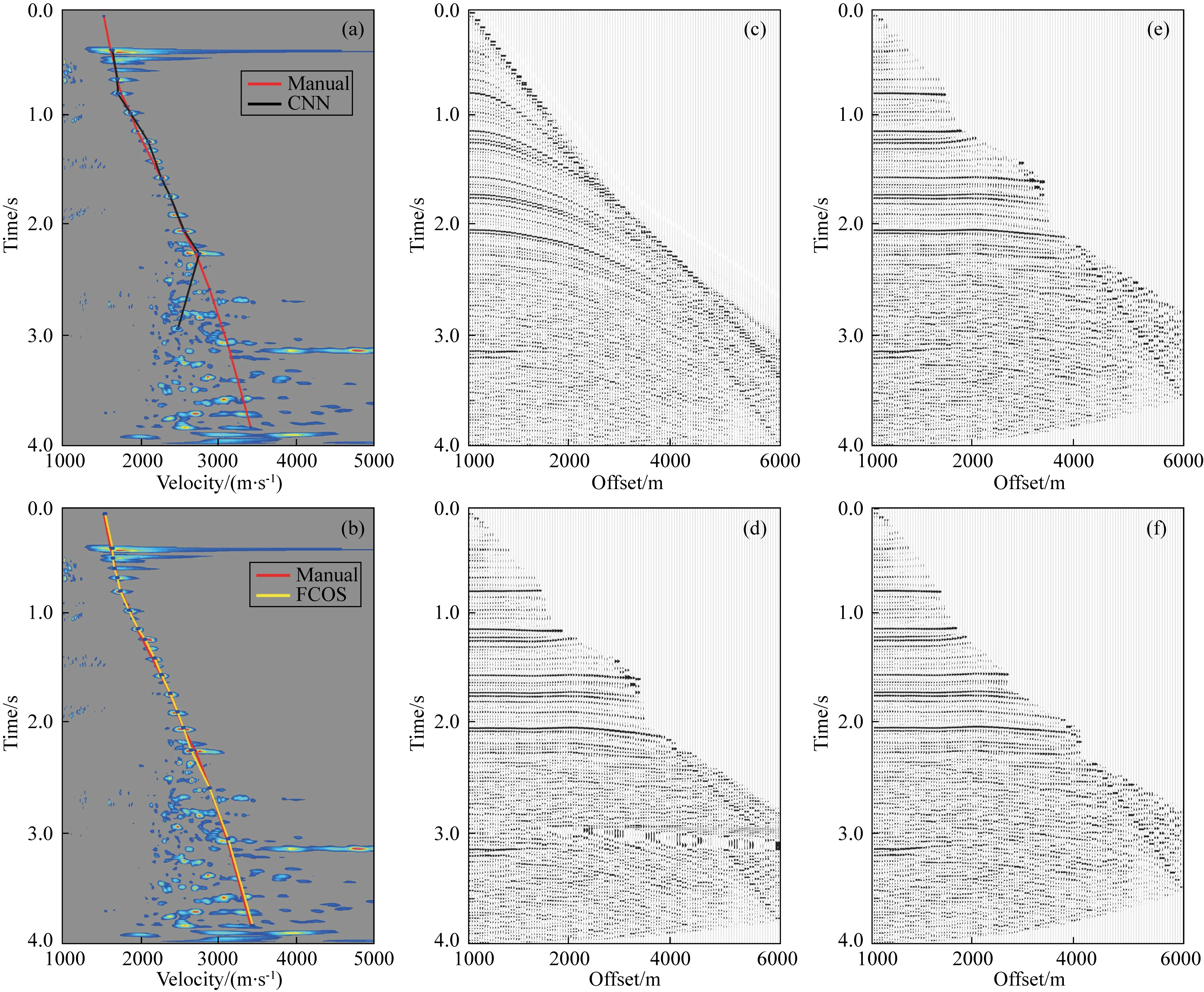
图6 Marmousi模型预测结果（a）传统CNN方法拾取的速度曲线；（b）本文方法拾取的速度曲线；（c） CMP400道集；（d）传统CNN方法拾取速度动校正；（e）本文方法拾取速度动校正；（f）人工拾取速度动校正.Fig.6 Prediction results of Marmousi model（a） Velocity curve picked up by traditional CNN method;（b） Velocity curves picked up by the method in this paper;（c） CMP400 gather;（d） NMO gather corrected of the stacked velocity picked up by traditional CNN method;（e） NMO gather corrected of the stacked velocity picked up by the method in this paper;（f） NMO gather corrected of the stacked velocity picked up by manual method.

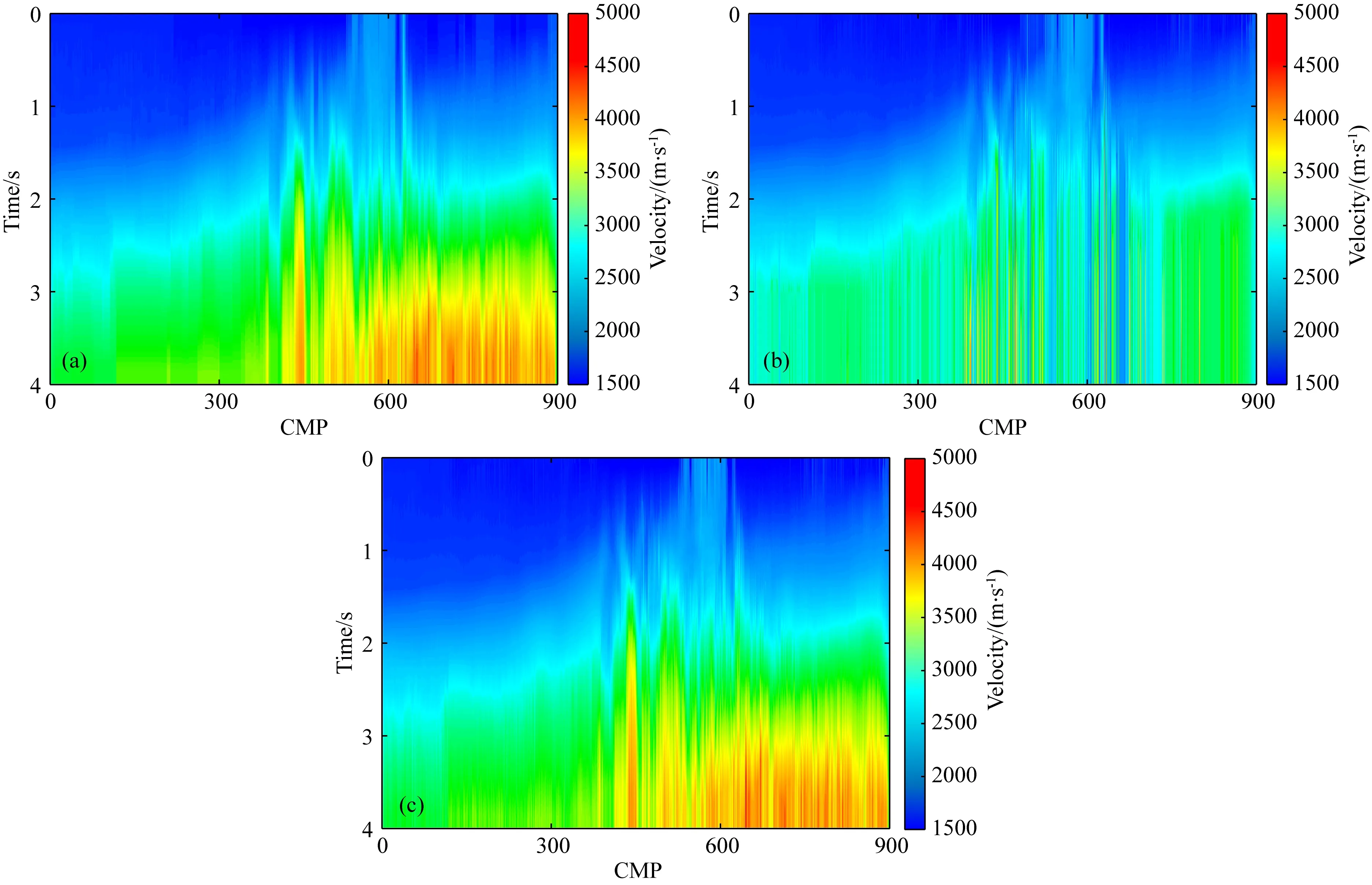
图7 Marmousi模型叠加速度场（a）人工方法拾取的速度场；（b）传统CNN方法自动拾取的速度场；（c）本文方法自动拾取的速度场.Fig.7 Stacking velocity field of Marmousi model（a） The velocity field picked up by manual method;（b） Velocity field automatically picked up by traditional CNN method;（c） The velocity field automatically picked by the method in this paper.

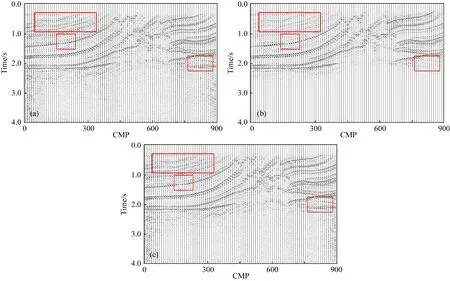
图8 Marmousi模型叠加剖面（a）人工方法拾取的速度场叠加；（b）传统CNN方法自动拾取的速度场叠加；（c）本文方法自动拾取的速度场叠加.Fig.8 Stacked sections of Marmousi model（a） The Stacked section of velocity field picked up by manual method;（b） The Stacked section of velocity field picked up by traditional CNN method;（c） The Stacked section of velocity field picked up by the method in this paper.

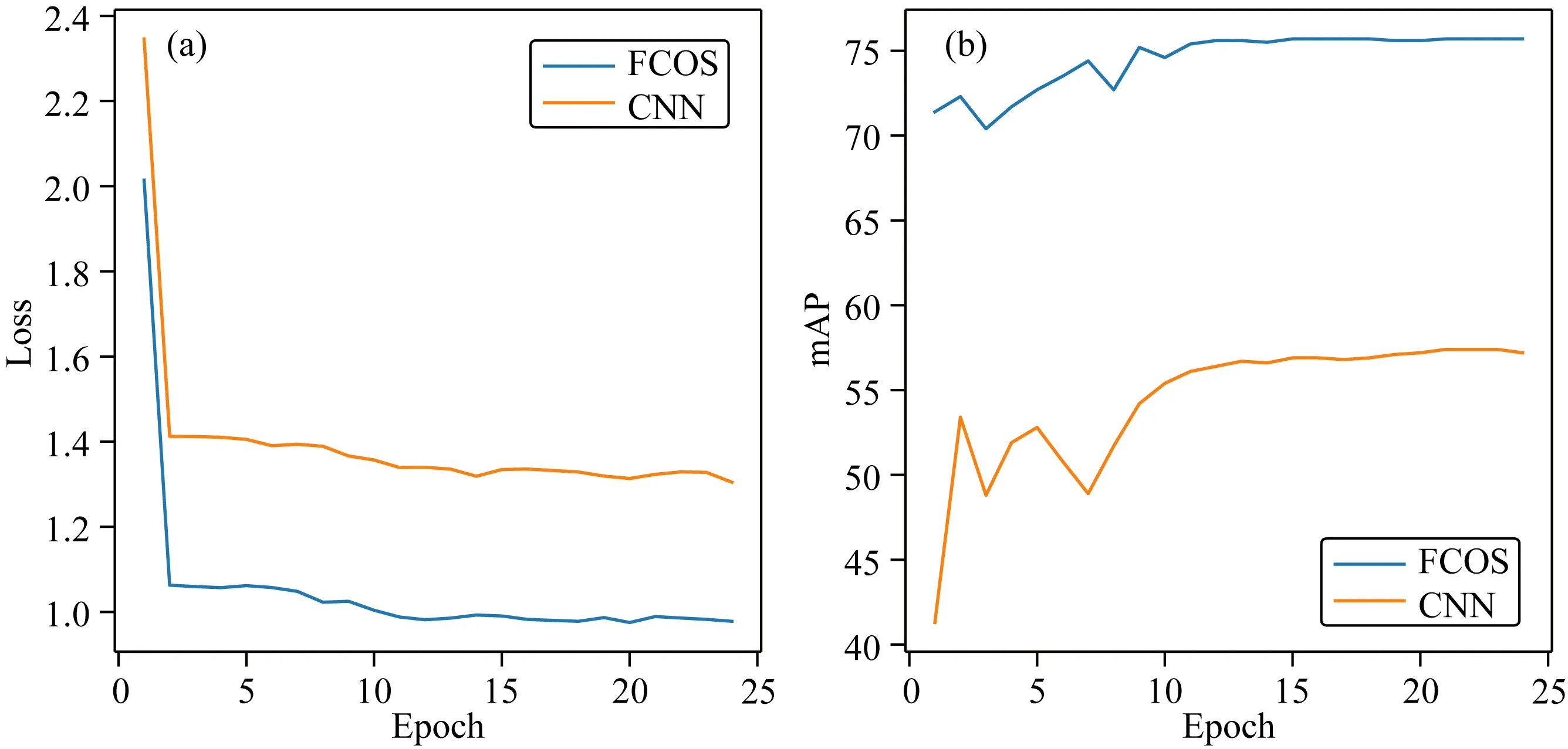
图9 实际探区数据Loss曲线图（a）及mAP曲线图（b）Fig.9 Actual exploration area data loss curve （a） and mAP curve （b）

图10 实际数据CMP道集（a）传统CNN方法拾取的速度曲线；（b）本文方法拾取的速度曲线；（c） 2560测线CMP2240道集；（d）传统CNN方法拾取速度动校正；（e）本文方法拾取速度动校正；（f）人工拾取速度动校正.Fig.10 CMP gather of actual data（a） Velocity curve picked up by traditional CNN method;（b） Velocity curves picked up by the method in this paper;（c） CMP2240 gather in the2560Line;（d） NMO gather corrected of the stacked velocity picked up by traditional CNN method ;（e） NMO gather corrected of the stacked velocity picked up by the method in this paper;（f） NMO gather corrected of the stacked velocity picked up by manual method.

对整个Marmousi模型数据集进行预测，并将本文方法自动拾取的叠加速度场（图7c）与传统CNN方法得到的叠加速度场（图7b）和人工方法得到的速度场（图7a）进行对比.总体上看，本文方法拾取的速度场在构造刻画与连续性上与人工方法得到的速度场基本相同；而传统CNN方法拾取的速度场在深层区间（2.5～4.0 s）内速度值偏小，且横向连续性较差.以CMP间隔为10将动校正后的道集进行同相叠加形成叠加剖面.与传统CNN方法得到的叠加剖面（图8b）相比，使用本文方法得到的叠加剖面（图8c）在浅层成像更加清晰，对构造细节刻画地更为准确，而传统CNN方法得到的叠加剖面受多次波等因素的影响，在浅层部分区间同相轴横向波动较大，在3.0 s以后未见明显地震反射（如红色框所示）；与人工拾取拾取速度场得到的剖面相比（图8a），本文方法得到的叠加剖面在构造连续性与清晰度上与人工方法基本一致，这进一步证明了本文方法的有效性.

2.2 实际数据

基于模型数据的实验结果，分别选用不同信噪比的实际探区数据对传统CNN方法和本文方法进行了测试.首先选用中国西部某陆上三维探区真实数据集，该探区信噪比较高，偏移距展布范围为0～8 km，数据的时间总长度7 s，采样间隔为2 ms.从中等间隔抽取若干条测线，并以相同间隔从每条测线上抽取CMP道集，共获得包含1000张速度谱图像的数据集.将生成的数据集按 8∶1∶1分为训练集、验证集和测试集三部分，用于训练传统 CNN 方法和本文方法设计的速度谱识别模型并对实验结果进行测试.训练过程中梯度下降损失和推理过程中mAP精度表现如图9所示.从图9中可以看出本文方法计算梯度下降得到的Loss曲线更为收敛，且应用本文方法训练的目标检测器在Marmousi数据集上的mAP精度最高为75.7，而传统CNN方法在Marmousi数据集上的mAP精度最高仅为57.4.

图10展示了采用两种方法得到的2560测线上CMP2240道集的速度拾取结果及动校正前后的道集.为了增加对比效果，将人工拾取的速度曲线与网络模型自动拾取的速度曲线可视化到同一个速度谱中.图10（a,b）分别展示了两种方法的拾取结果，从速度谱中可以看出在3.5 s后虽然受到多次波的干扰，且在5 s以后能量团横向较为分散，但FCOS方法自动拾取的叠加速度与人工拾取的叠加速度经插值处理后的曲线基本重合.而传统的CNN方法得到的速度曲线在3.5～4.5 s内波动较大，拾取结果明显偏离人工拾取速度值.图10c展示了动校正前的CMP2240道集图像，从中可以看出该道集浅层反射波时距曲线成像较为清晰，在深层区间（5 s以后）未见明显的反射双曲线.分别对两种方法的拾取结果进行动校正，采用FCOS网络模型自动拾取的叠加速度的动校正的结果如图10e所示，从图中可知FCOS方法拾取的叠加速度动校正结果的主要反射同相轴拉平程度与人工拾取速度动校正结果（图10f）相一致，这进一步展现了本文方法的稳健性.图10d展示了传统CNN方法得到的叠加速度的动校正结果，在3.7 s处该方法受低速值的影响错误的拉平了道集中的时距曲线，而在4.9 s处该方法又受低速值的影响，导致同相轴随偏移距增大出现上翘现象.

对第2560测线上的CMP道集进行测试，然后将应用两种方法得到的叠加速度场与人工拾取速度场进行对比.总体上看基于FCOS方法拾取的速度场（图11c）与人工拾取速度场（图11a）在构造上基本一致，且通过本文方法得到的速度场在横向上速度走势更加平稳；而传统CNN方法得到的速度场（图11b）在4.5 s以后速度值偏小，且在横向分布上较为散乱，未出现明显的速度分界面.为了进一步展现结果的准确性，本文展示了采用FCOS方法所得到的第2560测线上局部叠加剖面（图12c）与和人工拾取叠加剖面（图12a）的对比，从图中可以看出FCOS方法得到的叠加剖面与人工拾取结果非常近似；而传统CNN方法得到的局部叠加剖面（图12b）与本文方法相比，其在3.5 s后由于受多次波能量团的影响导致拾取的速度值偏低，在地震剖面上出现多次波能量聚焦效应，同相轴更为清晰（如红色框所示）.

然后，采用中国西部某三维探区的信噪比较低的CMP道集数据进一步测试本文方法.该探区偏移距展布范围为0～7 km，数据的时间总长度8 s，采样间隔为2 ms.从中等间隔抽取若干条测线，并从每条测线上等间距抽取CMP道集，共获得包含1000张速度谱图像的数据集，进而采用在上述实际探区中所训练模型来测试本文方法的泛化性能.由于该探区信噪比低，在叠前道集中未见明显的反射波时距曲线，本文只展示出传统CNN方法与本文方法得到的预测结果与人工拾取结果的对比（图13）.由图中可以看出该探区数据质量不高，速度谱上的能量团聚焦特性较差.传统CNN方法仅拾取到了0～3 s区间内的叠加速度（图13a），且在1.1 s处和2.0 s处拾取到部分高速异常值，在3～8 s区间范围内由于速度谱能量团较为分散，传统CNN方法未能自动拾取.图13b展示了仅使用FCOS方法（图中黄线）的拾取结果，该方法仅能拾取到0～4 s区间内的叠加速度，由于其不满足时间域全局的拾取要求，本文在FCOS网络的基础上加入一个基于DNN的线性回归模型，即通过学习0～4 s区间内的叠加速度的线性趋势来完成对4～8 s区间内的叠加速度的预测，最终的预测结果如图13b（绿线+黄线）所示.由图可知在加入线性归回模型后本文算法的输出结果与人工拾取结果基本相符.

图14展示了人工拾取速度场（图14a）、传统CNN方法拾取的速度场（图14b）和本文方法拾取的速度场（图14c）的比较.受信噪比较低的影响，传统CNN方法只能拾取到0～3 s区间的速度场，且在部分道存在低速或高速速度异常导致横向连续性较差，在3.0 s以后的速度相较人工拾取速度场中的速度值普遍偏低.而本文方法拾取的速度场在速度变化趋势上与人工拾取速度场相一致，但由于应用本文方法拾取速度场并未充分考虑道间相似性，拾取结果在横向连续性上相较人工拾取速度场较差，在速度分界面处的速度值较为发散.对上述三种方法拾取的道集进行动校正和叠加处理后得到叠加剖面.总体来看，本文方法的叠加剖面（图15c）与人工拾取结果（图15a）相近；在红色框所示位置使用本文方法得到的同相轴相较传统CNN方法（图15b）表现更为连续，这进一步检验了本文拾取结果的准确性.

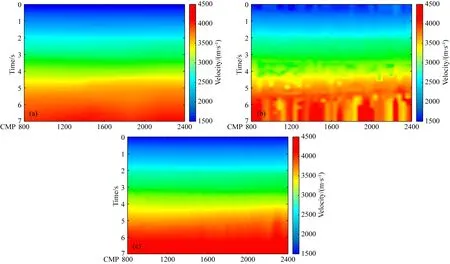
图11 实际探区速度场（a）人工方法拾取的速度场；（b）传统CNN方法自动拾取的速度场；（c）本文方法自动拾取的速度场.Fig.11 The actual velocity field in the exploration area（a） The velocity field picked up by manual method;（b） Velocity field automatically picked up by traditional CNN method;（c） The velocity field automatically picked by the method in this paper.

图12 实际地震资料叠加剖面（a）人工方法拾取的速度场叠加；（b）传统CNN方法自动拾取的速度场叠加；（c）本文方法自动拾取的速度场叠加.Fig.12 Stacked sections ofactual seismic data（a） The Stacked section of velocity field picked up by manual method;（b） The Stacked section of velocity field picked up by traditional CNN method;（c） The Stacked section of velocity field picked up by the method in this paper.

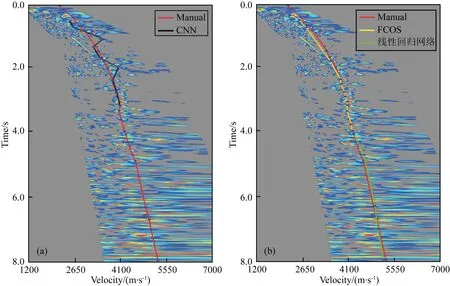
图13 实际数据速度曲线（a）传统CNN方法拾取的速度曲线；（b）本文方法拾取的速度曲线.Fig.13 Velocity curve of actual data（a） Velocity curve picked up by traditional CNN method;（b） Velocity curves picked up by the method in this paper.

图14 拾取的速度场与真实速度场比较（a）人工方法拾取的速度场；（b）传统CNN方法自动拾取的速度场；（c）本文方法自动拾取的速度场.Fig.14 The actual velocity field in the exploration area（a） The velocity field picked up by manual method;（b） Velocity field automatically picked up by traditional CNN method;（c） The velocity field automatically picked by the method in this paper.

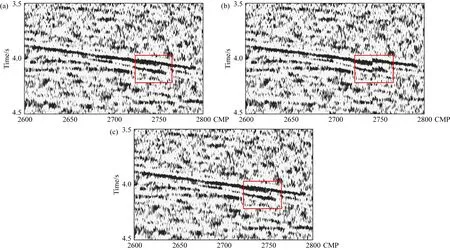
图15 实际地震资料叠加剖面（a）人工方法拾取的速度场叠加；（b）传统CNN方法自动拾取的速度场叠加；（c）本文方法自动拾取的速度场叠加.Fig.15 Stacked sections of actual seismic data（a） The Stacked section of velocity field picked up by manual method;（b） The Stacked section of velocity field picked up by traditional CNN method;（c） The Stacked section of velocity field picked up by the method in this paper.