考虑摩阻损失的稠油油藏水平井产能计算新方法
2022-12-02孙召勃贾晓飞杨馥榕
孙召勃,贾晓飞,杨馥榕
(1.中国海洋石油国际有限公司,北京 100028;2.中海石油(中国)有限公司天津分公司,天津 300459)
0 引言
渤海油田稠油资源具有储量规模大、油藏埋藏深、黏度范围广等特点,水平井是开发稠油油藏的有效手段之一[1-3]。目前已有学者提出了稠油油藏水平井产能计算公式,但其中只有极少数人考虑到井筒摩阻损失,且相关的井筒摩阻计算均采用了牛顿流体管流模型,不符合非牛顿流体的管流特征,夸大了摩阻的影响[4-13]。客观准确计算非牛顿流体特性和摩阻损失的影响,对优化水平井长度、准确预测产能意义重大[14-20]。
该文同时考虑稠油油藏的非牛顿特性和水平井段的摩阻损失,利用渗流阻力法建立了幂律型稠油油藏水平井产能计算模型,分析了水平井长度、幂律指数和稠度系数对水平井产能的影响,为评价幂律型稠油油藏水平井产能提供理论指导。
1 幂律型稠油油藏水平井产能模型
幂律型流体的流变性表征方程为:
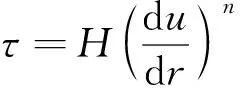
(1)
式中:τ为剪切应力,MPa;n为幂律指数;H为稠度系数,mPa·sn;r为径向距离,m;u为速度,m/s。
幂律型稠油油藏中流体的运动方程为:

(2)
其中:
μb=μeffvn-1
(3)

(4)
式中:v为渗流速度,m/s;k为渗透率,mD;p为压力,MPa;μb为幂律流体的视黏度,mPa·s;μeff为等效黏度,mPa·s;φ为孔隙度。
1.1 地层中的渗流阻力
将水平井的渗流场简化为2个相互连接的渗流区域,第1流动区域为平面上从驱动边界流向水平井方向的渗流区,该区域受储层厚度控制;第2流动区域为垂直平面内围绕水平井段向水平井的渗流区,该区域渗流受水平井长度控制。
1.1.1 外部平面内径向流
外部平面渗流场可近似为稳定的平面径向流,相当于泄油半径为re、厚度为h的圆柱体泄油区向井筒半径为L/4的“直井”渗流。
由式(2)和式(3)可得外部稳定渗流时径向流方程为:

(5)
式中:qh为外部平面内径向流的流量,m3/d;Bo为原油体积系数;h为储层厚度,m。
对式(5)进行分离变量法求解,可得外部平面内径向流流量为:
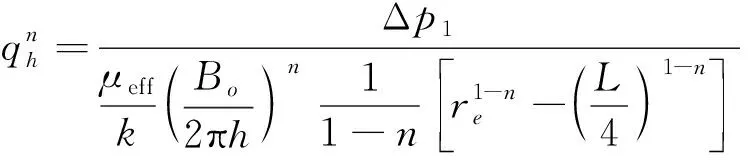
(6)
式中:Δp1为外部平面内径向流区域的压差,MPa;re为供给半径,m;L为水平井的水平井段长度,m。
1.1.2 内部垂直面内径向流
在垂直平面上,水平井渗流场受水平井段L控制,垂直径向流外部边界半径为h/(2π),内部边界半径为井半径rw。由式(2)和式(3)可得稳定渗流时径向流方程为:
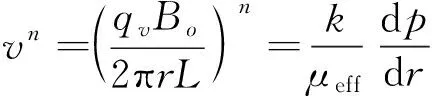
(7)
式中:qv为内部垂直面内径向流的流量,m3/d。
对式(7)进行分离变量法求解,可得内部垂直面内径向流流量为:
(8)
式中:Δp2为内部垂直面内径向流的压差,MPa。
1.2 水平井段井筒摩阻损失
由于原油黏度较大,流量相对不高,在水平井段内通常出现层流,即流体只沿着轴向流动而无横向运动。
水平井段内层流的流量为:
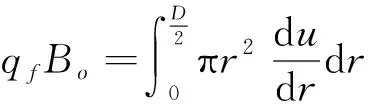
(9)
式中:qf为水平井段内层流的流量,m3/d;D为水平段井筒的直径,m。
将式(1)带入式(9)并分部积分可得:

(10)
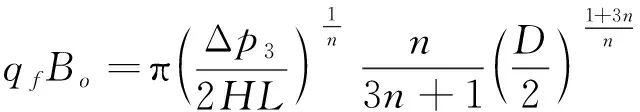
(11)
式中:Δp3为井筒附加压降,MPa。
式(11)变形可得:

(12)
1.3 水平井产能计算公式
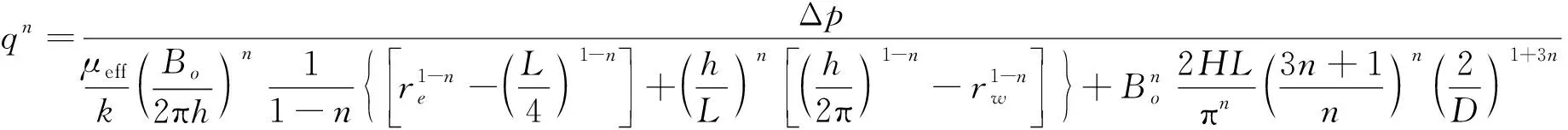
(13)
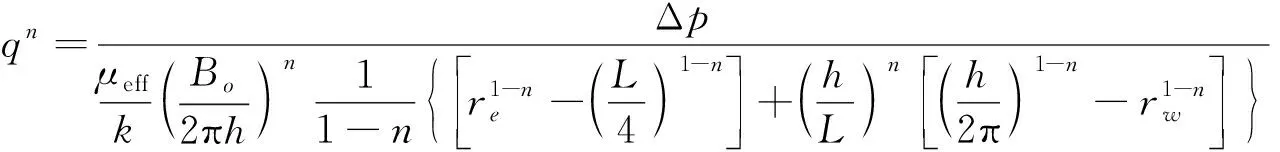
(14)
式中:q为水平井产量,m3/d;Δp为总的生产压差,MPa。
2 公式适应性分析
由于n趋于或等于1时,存在如下关系式:
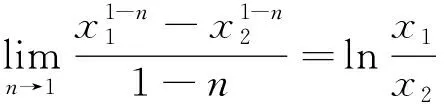
(15)

(16)
因此,当流体逐渐由幂律型流体趋于牛顿流体时,若不考虑摩阻损失,式(14)可逐渐接近直至变为Borisov水平井产能公式[14]:
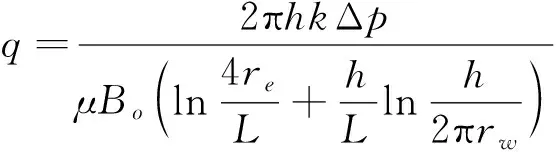
(17)
而对于层流摩阻而言,在n=1时,水平井段井筒内摩阻损失造成的渗流阻力退化为常见的牛顿流体层流造成的渗流阻力:
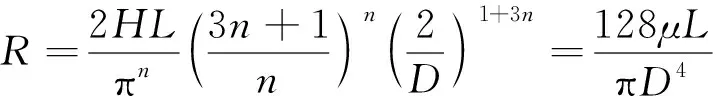
(18)
式中:R为水平井段内的渗流阻力,MPa·d·m-3。
综合以上分析,n=1时,式(13)可以简化为考虑摩阻损失的常规油藏水平井产能公式:
(19)
由上述分析可知,式(13)是适用范围更广的考虑摩阻损失的幂律型稠油油藏水平井产能公式,Borisov水平井产能公式和牛顿流体摩阻损失公式都是其特例。
分别利用上述产能公式对水平井产量进行实例计算,对比分析各公式的适应性。
已知油藏基本参数为:re=1 000 m,rw=0.12 m,L=500 m,k=3 000 mD,h=30 m,φ=0.3,Bo=1.08,n=0.9,H=100 mPa·sn。水平井生产压差Δp=2 MPa,实际产量为38.50 m3/d。采用不同的方法计算水平井产量,结果见表1。
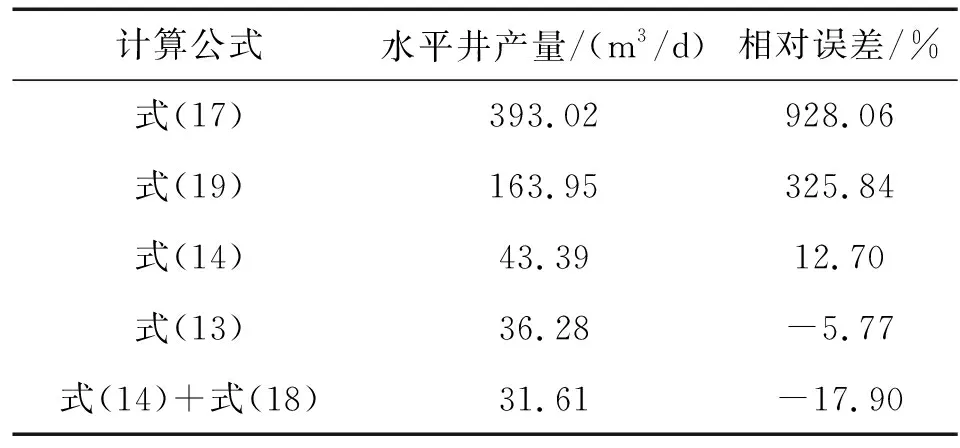
表1 各种方法计算的水平井产量结果Table 1 Production results of horizontal wells calculated by various methods
由表1可以看出,式(17)和式(19)计算结果远大于实际值,说明非牛顿特性对产能影响很大,不可忽略;考虑非牛顿特性的后3种计算方法所得结果误差明显降低,其中考虑非牛顿流体管流摩阻的式(13)计算误差最小,仅为-5.77%,其他2个公式相对误差的绝对值大于10%,尤其是地层渗流阻力采用非牛顿流体而管流摩阻损失采用牛顿流体的最后一种方法,放大了摩阻损失的影响,误差较大,低估了水平井产能。综上对比分析,该文所建立的综合形式得到的式(13)考虑因素最为全面、准确,误差最小,满足工程要求,可以用于矿场实践。
3 产能影响因素分析
3.1 水平井长度
当其他参数一定时,计算不同水平井长度下的产能,如图1所示。图1中蓝线为考虑了摩阻损失的幂律型稠油油藏水平井产能公式,红线为对应公式在不考虑摩阻损失情况下的形式。由图1可以看出,水平井越长,两公式求得的水平井产量越高。其中,考虑了摩阻损失的公式计算出的产能相对更低,且随着水平井长度的不断增加,产能的增加幅度也逐渐变小。当水平井长度超过600 m后,由于摩阻损失造成的产能降低超过了20%。根据Dikken研究成果可知,此地层流体参数下水平井最优长度为600 m,因此对于稠油油藏而言,水平井不宜过长。

图1 水平井长度对产能的影响Fig.1 Influence of horizontal well length on productivity
3.2 幂律指数
当其他参数一定时,计算不同幂律指数对水平井产能的影响,如图2所示。由图2可以看出,随着幂律指数的降低,考虑了摩阻损失的幂律型稠油油藏水平井产能公式和不考虑摩阻损失情况下的产能公式计算出的产量均明显降低,且当幂律指数下降至0.9时,两者的产能降低都超过了80%。幂律指数的下降表示原油的非牛顿特性增强,从而影响了水平井的产能。因此,在矿场实际生产中,对于强非牛顿特性的稠油,通过物理化学等手段降低非牛顿特性可以显著提高水平井产能,是重要的增产措施之一。
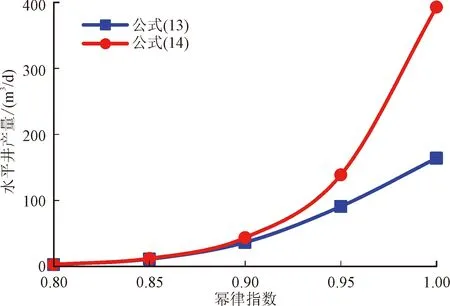
图2 幂律指数对产能的影响Fig.2 Influence of power-law index on productivity
3.3 稠度系数
当其他参数一定时,计算不同稠度系数对水平井产能的影响,如图3所示。由图3可以看出,随着稠度系数的增大,两公式计算出的水平井产量均不断降低,且降低幅度逐渐减小。由于稠度系数反应了非牛顿流体的黏性程度,随着稠度系数增大,相应的剪切黏度和有效黏度也会增大,渗流阻力增加,因此导致水平井产能降低。
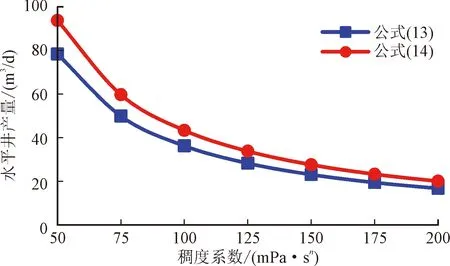
图3 稠度系数对产能的影响Fig.3 Influence of consistency coefficient on productivity
4 矿场应用
S油田为某典型稠油油藏,部署4口水平井进行局部细分层系调整。已知基本参数为:rw=0.12 m,φ=0.31,Bo=1.08,n=0.95,H=186 mPa·sn,其他参数及产量见表2。采用新方法计算的产能结果相对误差小于7%,满足矿场要求。
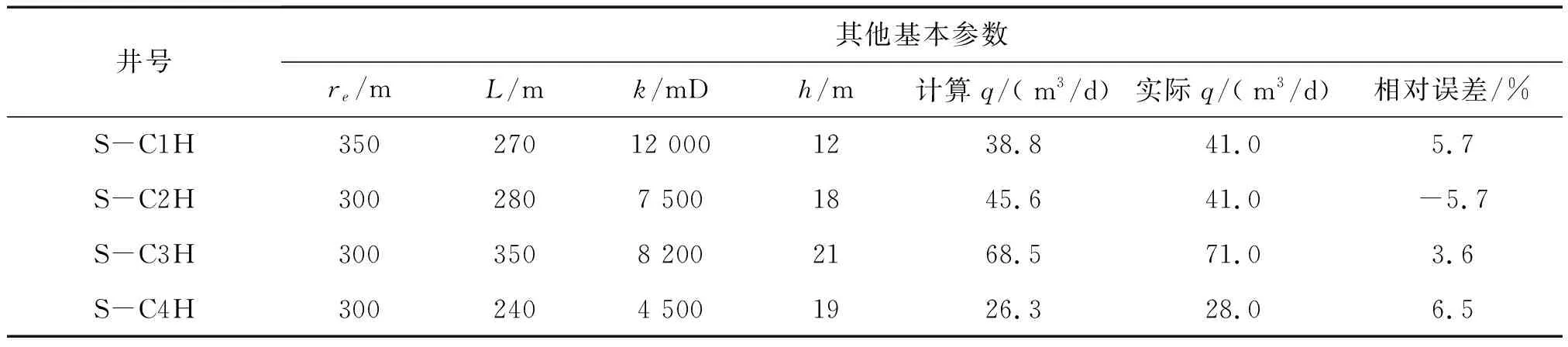
表2 4口井其他基本参数
5 结论
1)利用幂律型稠油油藏水平井产能计算公式,研究了水平井长度对稠油油藏产能的影响。结果表明,水平井越长,产能增加幅度越小,水平井长度超过600 m后,摩阻损失造成的产能降低将超过20%。
2)稠油的非牛顿流体特性对水平井产能影响显著,原油的非牛顿特性越强,水平井产能下降越明显,当幂律指数下降至0.9时,产能降低超过80%。
3)矿场实例表明,综合考虑了非牛顿流体特性和摩阻损失后建立的幂律型稠油油藏水平井产能公式计算误差最小,仅为-5.77%,较常用公式适应性更强,计算结果更准确,更能满足工程要求。
