寒区隧道洞口段空气幕保温理论研究
2022-12-02王仁远朱永全方智淳张红钰王道远
王仁远,朱永全,高 焱,方智淳,张红钰,王道远
(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;2.淮阴工学院 交通工程学院,江苏 淮安 223003;3.河北建设集团天辰建筑工程有限公司,河北 保定 071000;4.河北交通职业技术学院 路桥工程系,河北 石家庄 050035)
我国的寒区面积为417.4×104km2,占国土面积的43.5%[1],随着交通运输网的日益完善,铁路、公路建设逐渐向高海拔和高纬度的寒区扩展延伸,因此隧道的防寒保温措施将成为工程建设期间注重的问题之一。
在实际监测方面,国外学者认为,2 km以上的寒区隧道内,洞口到隧道中部的温度最多可差15 ℃[2]。乜风鸣[3]在寒季观测记录了西罗奇2号隧道、杜草隧道和奎先隧道内的温度,结果显示离洞口越远,洞内气温越高。赖金星[4]详细测试了青沙山公路隧道内部温度,分析得出隧道温度场受外界环境温度和自然风的影响较大。晏启祥等[5]对高寒地区某隧道温度场进行测试分析,得出该隧道处于低温环境4 d后出现冻害,铺设3 cm厚硬质聚氨酯泡沫可将二衬温度控制在0 ℃以上。赖远明等[6]以达坂山隧道为依托,并结合了多座寒区隧道的温度数据,归纳了围岩最大冻结深度与气温的关系。陈建勋等[7]对某寒区公路隧道的11个断面进行测试,得出隧道洞内年气温随时间呈正弦曲线变化。在理论计算方面,文献[8-9]依据热传导方程,得出具有隔热层的圆形隧道解析解。夏才初等[10]采用积分法和数值模拟,得出围岩最大冻结深度的解析公式。张学富等[11]建立渗流场与温度场的耦合计算模型,应用Galerkin法计算了两者的影响关系。张玉伟等[12]以寒区隧道温度实测数据为基础,建模讨论了冻胀力与围岩冻结深度的变化规律。
目前寒区隧道最常见的保温措施为铺设保温层法[13-14],但通过前人的研究成果可发现,传统保温层法应对外界环境较为被动,只能减小热量的传播和冻融速度[6],因此研制主动保温措施将成为未来寒区隧道的发展方向。本文通过寒区隧道温度场模型试验,得出寒区隧道温度场分布的一般性规律;在此基础上,提出一种适用于寒区隧道的空气幕保温措施,使用流函数叠加与热平衡原理,构建空气幕保温措施的控制方程,使用微分方程叠加原理及贝塞尔特征函数得出在空气幕的作用下,隧道洞口围岩的径向温度理论解;最后以正盘台隧道为算例,利用有限元软件Ansys Fluent验证控制方程及解析解的准确性,模拟保温效果,从而证明空气幕保温措施的可行性。
1 寒区隧道温度场模型试验
如今对寒区隧道温度场的研究主要依靠现场实测的方法,而复杂多变的自然环境随时会影响测量结果,增加数据分析难度。因此,将原有结构按一定比例缩小后,在试验室中人为调控各项变量,可以方便总结出寒区隧道温度场的一般性规律。
1.1 模型试验的组成
当模型试验和原有结构在几何、动力、运动、边界和起始条件等方面均相似时,可以保证两者的测试结果相同。通过相似理论的验证,研发自制了几何相似比50∶1、计算时间相似比10∶1、列车速度相似比5∶1、温度相似比1∶1的寒区隧道温度场模型试验装置,见图1,试验台研发过程见文献[15]。

图1 模型试验台设计
试验台操作方法为
(1)将保温隔板放置在冷域与隧道模型之间,通过外界温度调控系统将制冷空气由进风管吹入冷域中,再由出风管流回(制冷范围为-40~40 ℃),使冷域温度达到试验所需的外界温度。制冷期间用保温材料将冷域、进风管和出风管包裹,以减小冷气与屋内环境的对流换热作用。
(2)试验时将围岩温度设为恒温边界条件,通过围岩温度调控系统加热循环介质到设定的温度后(温度调控范围为0~40 ℃),将循环介质不断地从进水管推入隧道模型的保温夹层中,再从回水管流回围岩温度调控系统。
(3)为保证循环介质接近0 ℃时不结冰,选用乙二醇∶水=3∶7的混合液体作为循环介质。
(4)隧道模型共有22段,每段长度为1.154 m,在每段的1/3和2/3处设有温度和风速测试孔。
(5)将列车模型和加速滑块固定在高强度皮带上,通过伺服电机驱动,精准控制列车的运行速度,(最大速度可到达108 km/h)。
1.2 试验可靠性验证
本文采用控制变量法,研究在不同外界温度、围岩温度、列车运行速度情况下寒区隧道温度场的变化规律,试验流程见图2。
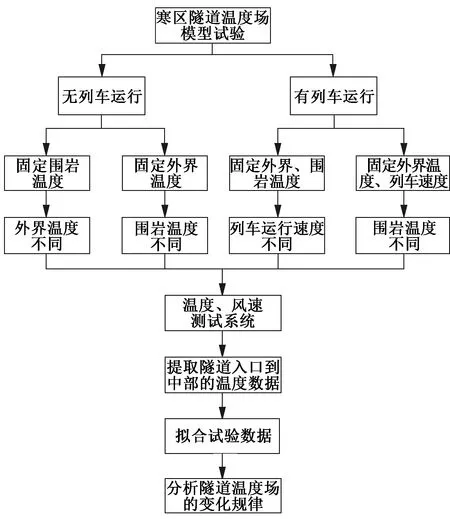
图2 试验流程
利用张家口崇礼的正盘台隧道实测温度验证试验台的可靠性。于2018年11月在隧道进口20~680 m处布置水银温度计作为温度测点,相邻2个测点间距60 m,连续测量30 d。外界平均温度取-7 ℃;隧道平均埋深400 m;围岩温度梯度取3 ℃/100 m[21],得到围岩温度为5 ℃。
1.3 试验结果分析
1.3.1 隧道内无列车运行时
(1)不同外界环境温度下,试验结果分析
当没有列车运行时,即不考虑列车风的影响,围岩温度设定为恒温10 ℃,外界环境温度设定为-5、-10、-15、-20、-25、-30 ℃。各温度条件下拟合公式见表1。试验3 d后,隧道内温度见图3(a)。由图3(a)可见,外界温度越低,隧道洞口段的温度也越低,洞内负温区长度越长,分别为190、270、400、510、610、700 m,计算得出外界环境温度每降低5 ℃,隧道内的负温区长度约增加102 m。
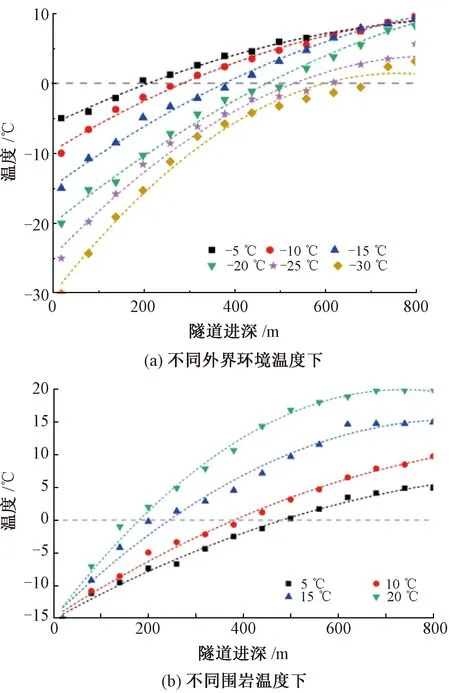
图3 无列车运行时隧道温度场分布规律

表1 各温度条件下拟合公式
(2)不同围岩温度下,试验结果分析
当没有列车运行时,外界环境温度设定为恒温-15 ℃,围岩温度设定为5、10、15、20 ℃,试验3 d后,隧道内温度见图3(b)。由图3(b)可见,随着围岩温度的增加,隧道内部的温度也逐渐增加,隧道中心处的空气温度约等于围岩温度;隧道洞口段处于负温状态,但是负温区的长度随着围岩温度的增加而减小,分别为500、400、210、150 m。计算得出围岩温度每增加5 ℃,隧道内的负温区长度约减小117 m。
综上可知,无论哪种工况下,隧道温度场均呈现进口低、中间高的抛物线形式,温度变化规律与其他学者提供的实测规律相同。以埋深每增加100 m,围岩温度增加3 ℃的标准来看,处于极端寒冷的温度条件下的隧道,虽然洞口段的温度较低,但是埋深较大的隧道依旧可以通过围岩地热与空气之间的对流换热作用,使内部保持正温,不会发生冻害现象。在寒区隧道防寒保温工程中,浅埋隧道应全段设防,保证隧道安全运营;深埋隧道洞口段必须设防,中心区域可根据实际情况选择是否设防。
1.3.2 隧道内有列车运行时
假定列车运行的时间间隔为30 min/次,列车运行速度分别为300、400 km/h时,外界环境温度为-15 ℃,围岩温度为5 ℃的条件下,试验3 d后隧道内温度分布见图4(a);若围岩温度设置为10 ℃,其他条件保持不变,试验3 d后隧道内气温分布如见4(b)。

图4 列车运行时隧道温度场分布规律
图4(a)显示,当外界环境温度为-15 ℃,围岩温度为5 ℃,隧道内列车运行间隔为30 min/次时,无列车运行和列车运行速度为300、400 km/h时相比,隧道洞内负温区的长度分别增加了约20、40 m,表明列车风对隧道内负温区长度的影响不大。图4(b)显示,当围岩温度升高至10 ℃时,三种工况下隧道内温度几乎相同,与图4(a)相比,说明了随着围岩温度的升高,列车风对隧道温度影响效果逐渐减小。当列车运行间隔大于等于30 min/次时,列车风对寒区隧道温度场影响效果不大,且围岩温度越高,列车风对隧道内温度的影响效果越小。
2 隧道洞口空气幕保温理论研究
通过第1节的模型试验结果可以看出,隧道洞口段与外界直接相连,受自然环境影响较大,最易发生冻害。若采取一种可以主动隔绝、加热寒冷空气的措施,将流入隧道洞内的温度控制在0 ℃以上,则可以有效消除冻害现象。基于此设想,本文提出一种新型的保温方法——隧道洞口空气幕保温措施。
早在1904年,Tephilus van Kemmel首次将空气幕安装在大门两边,成功隔断了由大门外面侵入室内的冷空气[16],现阶段空气幕广泛应用于不同场合:如高层建筑的防烟通风[17];地铁、车站、冷库屋内的保温隔热[18-19];以及矿山、矿井中排出废气,隔绝粉尘[20],但将空气幕作为隧道的防寒保温措施的研究仍在起步阶段。在洞口前搭建矩形棚洞,安置空气幕大门,高速、高温气流经空气幕喷口喷出,形成一道空气幕墙,主动阻隔并加热外界的寒冷空气,棚洞也可防止雨雪对空气幕的不良影响。同时考虑安装美观和行车安全,采用上吹式空气幕。该系统可根据不同地区的自然环境,设置空气幕的射流参数、架设数量、运转时间等,相比于隧道防寒门,更加安全和灵活。下面将通过理论分析与数值计算验证该措施的可行性。
2.1 隧道洞口流场分析
空气幕的计算模型见图5,其中水平方向为x轴,竖直方向为y轴。H为隧道口高度,ω0为空气幕入射口出风速度大小,m/s;b0为空气幕喷口厚度,m;α为空气幕射流与x轴的交角,即喷射角度。

图5 空气幕计算模型
根据图5的计算模型,设单位宽度自然风的流函数ψ1为

(1)
式中:ω为自然风速大小,m/s。
空气幕单位宽度气流的流函数ψ2为[21]
(2)
式中:a为端流系数。
则洞口气流的流函数ψ即为自然风流函数和空气幕流函数叠加,即
ψ=ψ1+ψ2
(3)
从式(3)可以看出,当x=0,y=0,即空气幕大门最低点时,ψ0=0,当x=H,y=0,即空气幕大门最高点时,ψH为
(4)
根据流体力学原理,两条流函数的差值即为以两条流函数为边界的体积流量,即高为H的洞门单位宽度的体积流量Q为
Q=ψH-ψ0
(5)
设
(6)
通过对隧道洞口的流场分析最终得到防寒空气幕流量的控制方程,则式(5)可以化简为
(7)
2.2 空气幕对自然风阻隔的控制方程
根据式(7)可知,高为H的隧道进入单位宽度的气流量Q是空气幕喷射的气流量和自然风流入的气流量之和,即
Q=Q0+Q′
(8)
式中:Q0为空气幕喷射的气流量ω0b0,m3/s;Q′为自然风进入隧道的气流量ωH,m3/s。
将式(7)代入式(8),最终可得到自然风量Q′的表达式为
(9)
若自然风的流量Q′=0,则说明空气幕可以完全阻隔外界自然风,使寒冷空气无法进入隧道。因此在完全阻隔自然风的情况下,根据式(9)可得空气幕喷口风速ω0为
(10)
2.3 空气幕气流与自然风流混合温度的控制方程
在一定的计算时长内,若隧道洞口无空气幕,隧道洞口处的温度应与自然风流的温度相同;若隧道洞口有空气幕,空气幕喷射气流在阻隔自然风时会发生热交换,进入隧洞的风温为空气幕气流与自然风混合之后的温度,因此根据热平衡原理可得
(11)
式中:T′为自然风流的温度,℃;T0为空气幕喷口气流的温度,℃;Tk为自然风流经过空气幕后,流入隧道内气流的混合温度,℃,应保证流入隧道内气流的混合温度Tf≥0,可以有效防止冻害现象的发生。
若室外温度随时间的变化趋势为F(t),即外界环境温度,该函数可通过对该地区的气温进行测量,最终得出该地区一年中气温或者一天中气温随时间的变化趋势。则空气幕温度与自然风温度混合之后的隧道洞内气体温度为
(12)
3 空气幕作用下寒区隧道围岩径向温度场的分布的解析解
实际中隧道断面是马蹄形,因此在求隧道围岩传热的解析解时,需作如下几点假设:①隧道的横断面视为规则圆形;②隧道周边围岩为均匀介质,即在计算区域内任意一点围岩的物理和化学性质都相同;③洞内气温只沿隧道的轴线方向发生变化;④计算过程中不考虑相变影响。根据上述内容,建立圆形隧道温度场计算模型,见图6。

图6 传热计算模型的平面示意
该模型的传热方程为
(13)
式(13)的边界条件为
(14)
T=Tcr=l,t>0
(15)
式(13)的初始条件为
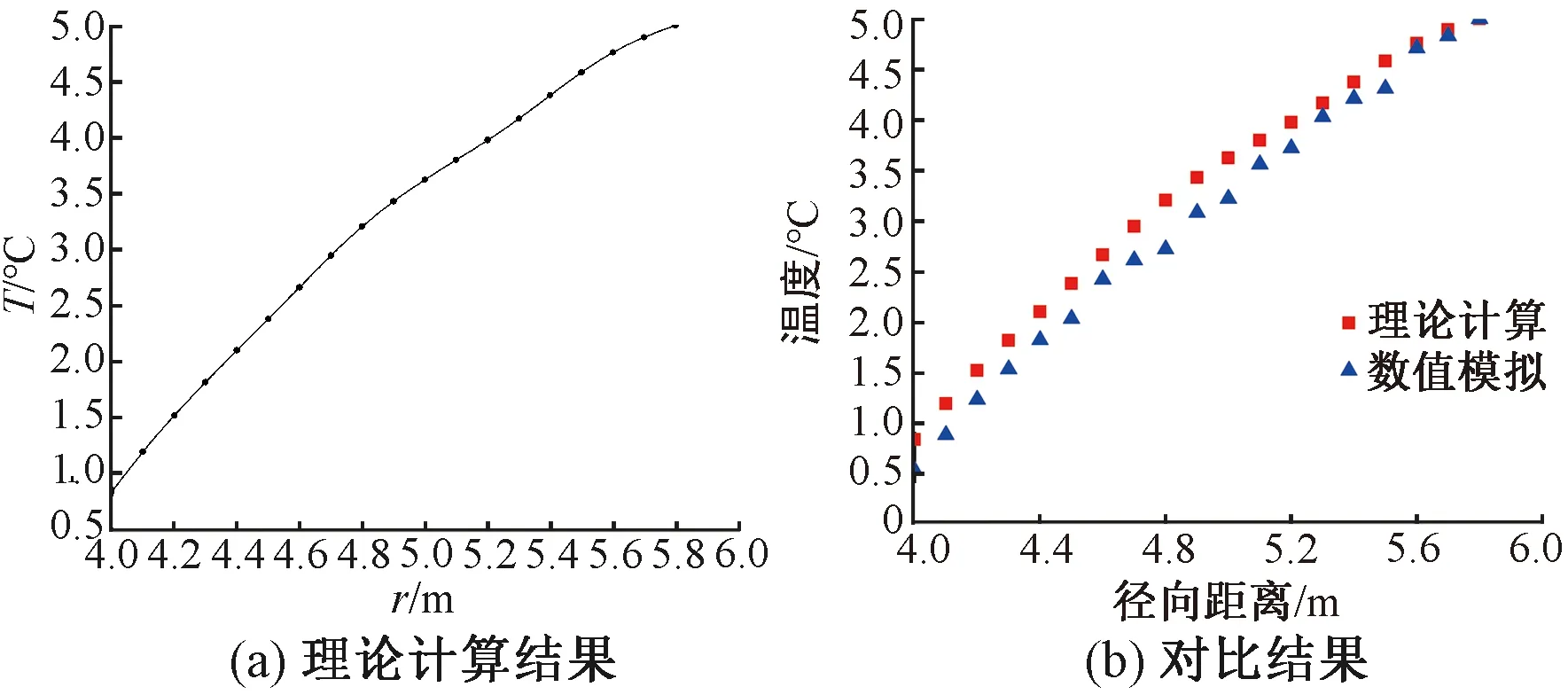
T=Tct=0,d (16) 隧道围岩的传热属于瞬态非齐次边界条件传热问题,可以通过叠加原理将非齐次边界条件转化成齐次边界条件,最终得出空气幕作用下围岩温度场的理论解。令P=Tk-Tc,将式(13)~式(16)做变量替换,把空气幕与自然风混合温度Tk(t)引入到式(13)的传热方程中,因此,式(13)改写为 (17) 式(17)的边界条件为 r=d,t>0 (18) P=0r=l,t>0 (19) 式(17)的初始条件为 P=0t=0,d (20) 采用叠加原理,将式(17)转化为式(21),即 P(r,t)=φ(r)[Tc-Tk(t)]+E(r,t) (21) 函数φ(r)与原方程有相同的定义域,是在r=d处有非齐次边界条件的稳态传热问题的解。 (22) 式(22)的边界条件为 (23) φ(r)=0r=l (24) 设P=φ′(r),则式(22)可写为 (25) φ(r)=C2lnr+C3 (26) 式中:C1、C2、C3为常数,将式(23)和式(24)的边界条件代入式(26),最终得到的φ(r)解析解为 (27) 函数E(r,t)与原方程有相同的定义域,具有齐次边界条件的非稳态传热问题的解,即 (28) 式(28)的边界条件为 (29) E(r,t)=0r=l (30) 当t=0时,E(r,0)=P(r,0)-φ(r)[Tk(0)-Tc]=0+φ(r)[Tc-Tk(0)],式(28)的初始条件为 t=0,d (31) 将E(r,t)分离变量可得 E(r,t)=ξ(r)η(t) (32) 将方程式(32)代入式(28)可得 (33) (34) 式(33)为时间变量的函数,其通解形式为 (35) 式中:βn为无穷多个特征值,且随着n越大,对结果的影响也就越小。 方程式(34)为贝塞尔微分方程,在文献[22]中已经通过贝塞尔函数的正交及展开定理给出通解形式。综上所述,式(28)的通解为 [A1C(βn)+B1D(βn)] (36) R0(βn,r)=J0(βnr)Y0(βnl)-J0(βnl)Y0(βnr) 再通过式(37)确定特征值βn为 (37) 式中:J0、J1为第一类贝塞尔函数;Y0、Y1为第二类贝塞尔函数。 最后,由式(21)、式(27)和式(35)即可得出在空气幕作用下,围岩径向温度场的解析解为 (38) 利用式(38)在空气幕作用下寒区隧道围岩径向温度场分布的解析解,对正盘台隧道进行算例验证,式(38)中第一部分可用初等数学计算,第二部分需借助Matlab数值计算编程软件求解计算。正盘台隧道为单洞双线隧道,是新建崇礼铁路一标段线路主体,是京张高铁第一长隧道。根据当地实测自然条件[23],以一月份最冷气温-10 ℃作为外界自然风温度,围岩初始温度Tc=5 ℃,空气幕大门高度与隧道净空相等,H=8 m,外界风速ω=2 m/s,空气幕喷口宽度b0=0.2 m,喷射角度α=30°,湍流系数a=0.2,在完全阻挡自然风的情况下,保证洞室内混合气体温度为0 ℃,根据式(10)和式(11)可得空气幕喷口的射流速度ω0=22.7 m/s,射流温度T0=35.24 ℃,围岩的计算参数见表2。利用Ansys Fluent有限元软件计算。在空气幕作用下,隧道内的风速和温度见图7。 表2 围岩参数 图7(a)的温度云图显示,为当外界自然风温度-10 ℃,空气幕喷口气流的计算温度35.24 ℃时,隧道内温度的分布规律。可以看到,空气幕喷出的气流形成一道幕墙,阻隔了外界自然风,射流外边界不断与自然风交汇混合形成了外混合区,冷热气流产生热交换;射流核心区较为稳定,最终流入隧道内。隧道洞口处气体温度已达到0 ℃左右,与计算结果相符合,随着隧道进深的增加,温度逐渐上升。从图7(b)的速度矢量图可以看到,自然风在洞口被阻隔后,向下弯曲射向地面,证明空气幕对于自然风有较好的阻隔作用。 图7 算例结果 隧道洞口未设置空气幕和设置空气幕时,温度的对比见图8。 图8 隧道洞口温度对比(单位:℃) 将混合后的温度0 ℃作为隧道进口的边界温度,经过一个月的冻结可以看出,洞口未设置空气幕时,隧道洞壁温度为-10~-8.5 ℃,与外界自然风温度相等,围岩的冻结深度约为1.8 m。而洞口安装空气幕时,洞壁温度在0.03~0.53 ℃左右,隧道内基本可以消除冻害现象。由此可见,对于寒区隧道而言,洞口设置空气幕,有较好的防寒保温效果。 将边界条件代入式(38)中可以验证,当r=d=4时,围岩温度为0.6 ℃;当r=l=5.8时,围岩温度为5 ℃。同时将表1中的参数代入式(38)中,利用Matlab进行数值求解,定义各参数取值,计算特征值βn,最后代入公式中,求解围岩径向温度场。在冻融圈范围4~5.8的范围内,取特征值βn的数量为18个,见表3。 表3 特征值取值 再将理论计算结果与数值模拟结果进行对比,见图9。 图9 模拟值与理论值 Matlab计算结果见图9(a),理论计算与数值模拟的对比结果见图9(b)。在空气幕作用下,隧道围岩温度均在0 ℃以上,从根本上防止了隧道内冻害的发生,同时理论计算和数值模拟的结果差别不大,可见式(38)可以较为准确的反映出空气幕作用下隧道洞口段径向温度的变化。 通过上述算例分析可以分析出,空气幕防寒保温措施的本质即,高速喷出的热空气作为射流源,阻隔外界寒冷自然风并与之进行热交换,最终消除隧道冻害,因此属于湍流、淹没射流。又根据射流边界条件的不同,可分为有限空间射流和无限空间射流。 (1)有限空间射流 (2)无限空间射流 图10 无限空间射流速度矢量(单位:m/s) (1)寒区隧道温度场模型试验得出,外界环境温度和围岩温度是影响寒区隧道温度场的主要因素,外界环境温度每降低5 ℃,隧道内的负温区长度约增加102 m;围岩温度每增加5 ℃,隧道内的负温区长度约减小117 m。 (2)浅埋隧道应全段设防,保证隧道安全运营;深埋隧道洞口段必须设防,中心区域可根据实际情况选择是否设防。一般情况下,列车风对于隧道温度变化影响较小。 (3)提出一种新型的寒区隧道主动保温措施,通过流函数叠加与热平衡原理,得出空气幕保温措施的控制方程。可用于计算完全阻隔外界自然风,且使隧道洞口气温保持0 ℃以上时,空气幕的射流速度和射流温度。 (4)利用叠加原理及贝塞尔特征函数正交、展开定理,推导出在空气幕作用下,寒区隧道洞口断面的径向温度理论解。将Matlab计算值与数值模拟进行对比分析,结果相差不大,该方程式满足一般的精度要求,可为今后工程实践提供理论基础。 (5)利用Ansys Fluent进行实际算例的建模计算,可以看出空气幕保温措施具有良好的防寒效果。同时根据边界条件的不同,将计算模型划分为有限空间射流与无限空间射流,分析了两种状态下隧道洞口的气流分布形式,在实际工程中可根据防寒保温的需要,选择经济合理的射流形式。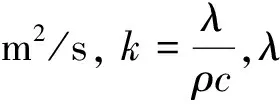
3.1 空气幕作用下隧道围岩径向传热方程
3.2 方程φ(r)的求解
3.3 方程E(r,t)的求解

4 算例分析
4.1 数值模拟结果分析

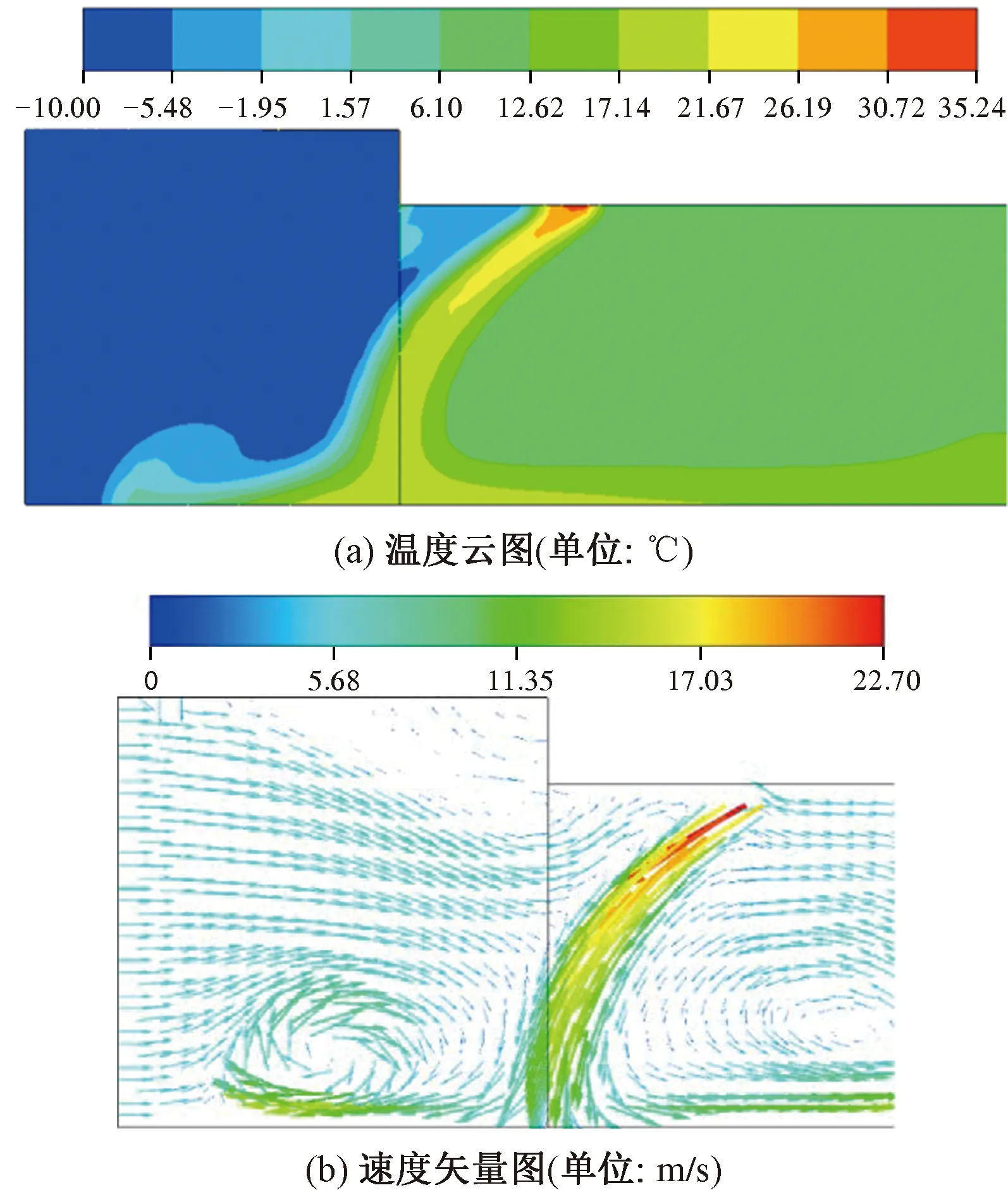

4.2 理论计算结果分析

4.3 空气幕射流属性及边界条件分析

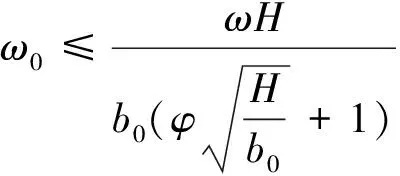

5 结论
