基于CNN的三相逆变器开路故障诊断及其样本条件分析*

申皓澜，唐 欣，罗毅飞，肖 飞，艾 胜，樊亚翔

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

基于绝缘栅双极型晶体管(insulated gate bipolar transistor, IGBT)等半导体开关器件的电能变换装置已被广泛应用于电网、舰船、高铁、电动汽车等重要领域，其安全可靠运行至关重要。然而，由于长期受电、热、振动等应力冲击，开关器件及其驱动、连接件面临着严峻的健康风险，是装置的主要故障源。据统计，装置中约38%的故障与开关器件有关[1]。

开关器件的故障主要包括短路和开路故障，其中短路故障伴随着大幅过电流现象，基于此已有集成于驱动的退饱和检测、集电极电流检测、快速熔断等成熟的硬件检测及保护方法，可在10 μs内迅速结束短路状态[1]。然而，开路故障的隐蔽性较强，可由IGBT键丝断裂、端子松动及破裂、驱动异常等众多因素引起，故障发生后装置通常能在一段时间内带故障运行而不触发系统保护。但是，开路故障仍会引起电压、电流畸变，如不及时诊断容易诱发严重的次生故障[2]。因此，对开路故障进行在线诊断具有重要的现实意义。

对电能变换装置整体输出电压或电流波形进行分析，是在较少传感条件下进行开路故障诊断的普遍途径[1-2]。其中，传统方法需要针对具体装置，人为地完成数据特征选择与提取、特征-故障解析建模、故障诊断机制设计等工作，当装置拓扑复杂度较高或结构发生改变时，存在建模难度大、诊断机制通用性弱等不足[3-4]。近年来，以数据驱动为基本特征的新一轮人工智能(artificial intelligence, AI)浪潮为开路故障诊断提供了如图1所示的重要思路，即利用装置的历史数据样本，采用机器学习、深度学习相关算法对样本与故障模式之间的复杂映射关系进行训练，自动建立具备故障诊断能力的“黑箱”模型[5-9]。

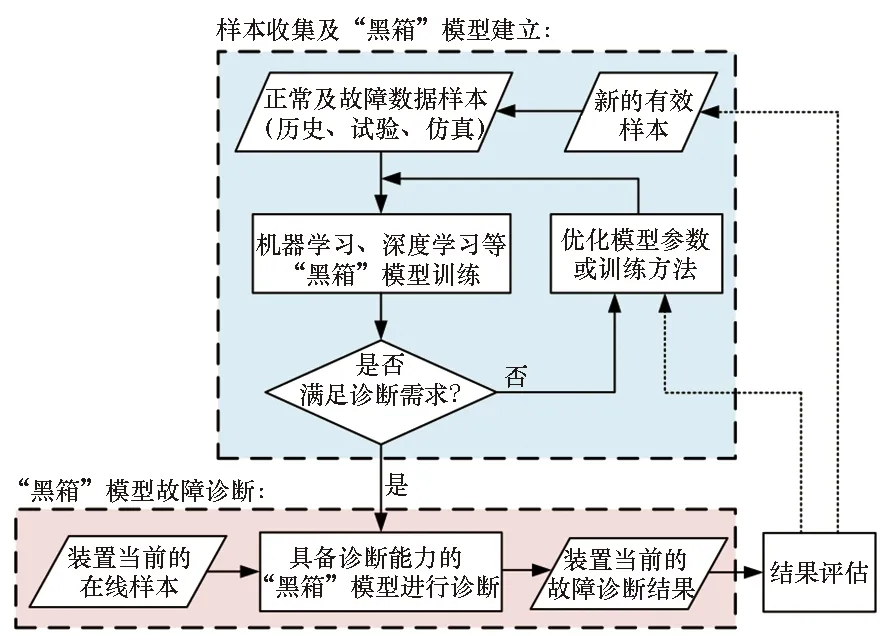
图1 基于“黑箱”模型的故障诊断基本思路Fig.1 Basic idea of data-driven fault diagnosis

对于各类具有一定数量规模和较高复杂度的装置，这种基于数据驱动和AI的“黑箱”方法在建模难度、诊断精度等方面具有明显优势，已逐渐在航空、风力发电、重型机械等领域成为保障装备可靠性的重要手段[10-12]。随着电能变换装置应用规模的增长、拓扑复杂度的提高，对其运行数据的积累及基于数据驱动和AI的故障诊断研究正日益凸显价值。

已有研究中，基于数据驱动和AI的电能变换装置开路故障诊断方法主要分为：将传统故障特征提取与支持向量机、浅层神经网络等相结合的机器学习方法；依靠深层神经网络的深度学习方法[4]。其中，机器学习方法是在人为提取方差、频谱峰值、小波能量等信号特征的基础上，利用机器学习来实现特征-故障模式映射；深度学习方法则采用多层神经网络，在较统一的训练方法下自动实现故障特征提取、故障诊断的完整过程，且往往能利用一些比人工特征诊断能力更优的深层抽象特征[13-14]。因此，深度学习方法具有更显著的智能化特点且容易得到更好的诊断结果。

在与神经网络有关的AI算法中，传统的误差反向传播(back propagation, BP)神经网络凭借清晰的多层全连接结构、较快的训练速度被广泛应用。然而，BP网络存在“参数膨胀”和“局部模糊”两个显著问题，即：全连接结构中待训练的权值数量会随着网络层数、神经元数量的增加而大幅增加；全连接结构难以深入提取和利用不同样本中一些存在位移、旋转、缩放等变换的局部特征[15-16]。这使BP网络较难构建层数较多的深层网络，且网络训练容易陷入局部最优和产生过拟合,需要进行优化[17-18]。目前，卷积神经网络(convolutional neural network, CNN)已成为深度学习的重要分支，其网络各层之间具有“网络局部连接”和“卷积核权值共享”两个鲜明特点，能够从改变“全连接”的根本上有效克服“参数膨胀”“局部模糊”带来的负面影响[19-20]。文献[21]利用CNN对电机振动信号进行处理，研究了一种考虑驱动速度因素的电机故障诊断方法，在降低诊断网络复杂度的同时提高了诊断准确性[21]。文献[22]利用CNN从感应电机定子电流的频率分量中提取故障特征，用于轴承故障在线诊断[22]。文献[23]将列车牵引电机的定子电流预处理为灰度图像，利用CNN全自动地提取特征并对变频器的IGBT开路进行诊断[23]。文献[24]使用CNN对三相电流进行处理，实现了对逆变器中单个IGBT开路的诊断[24]。但是，在基于神经网络的电能变换装置开路故障诊断研究中，普遍未充分分析样本条件对网络训练及诊断的影响，而直接使用数量较多、时长超基波周期的长样本来保证诊断准确率[24-25]。这会显著增加样本积累难度、硬件开销及耗时，不利于方法应用。

综上，本文以电能变换装置中典型的三相两电平逆变器为代表，将受负载影响较小的三相脉宽调制(pulse width modulation，PWM)电压作为开路故障样本，着重分析样本时长、样本数量变化时，CNN诊断方法相较于BP网络方法在网络权值数量、网络训练稳定性、诊断准确率上的优势，为实际应用中样本条件的选取提供有益参考。

1 三相两电平逆变器建模仿真与故障样本生成

1.1 三相两电平逆变器的Simulink建模

在MATLAB R2020a的仿真环境Simulink中，基于电气仿真模块Specialized Power Systems，搭建了如图2所示的三相两电平逆变器模型。主电路拓扑中包含编号为1#～6#的6个IGBT模块，采用典型的空间矢量脉宽调制方式。

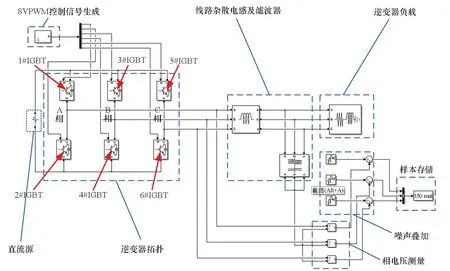
图2 三相两电平逆变器的Simulink模型及IGBT编号Fig.2 Simulink model and IGBT order of the three-phase two-level inverter

为使模型的运行条件接近真实工况，模型的母线电压、调制比、线路杂散电感、滤波及负载设置等均参考真实的1 MW逆变器。其中线路杂散电感、滤波等参数在完成设置后就成为系统中确定的一部分，不再对不同位置开路时监测信号的差异性造成影响。此外，即使考虑长期运行时的参数退化，以及负载在一定范围内的变化，它们也不是影响本文所监测的三相PWM电压的关键因素。总之，这些参数设置对后文开路诊断方法的建立及效果评价影响较小，因此不再做详细讨论。考虑到实际传感器的测量噪声影响，在模型输出电压上叠加了最大幅值约为0.5 V的高斯噪声。

该模型运行在50 Hz基波频率、5 kHz开关频率工况下。综合考虑：生成的故障样本须有效包含反映故障信息的IGBT开关状态，以保证开路诊断的准确率，此时要求采样频率应至少大于2倍开关频率；在保证足够信息量的前提下应尽可能减少冗余数据，从而减小CNN规模及计算量，即采样频率不应过大。最终设置模型采样频率为20 kHz，可较好权衡上述诊断准确率与计算量之间的矛盾。

模型使用1台便携式计算机进行仿真，硬件资源主要包括Intel i7-7700HQ CPU(主频2.8 GHz)、NVIDIA GeForce GTX 1050Ti GPU、16 GB RAM。未发生开路故障时，模型采集的一段30 ms三相PWM电压波形如图3所示，仿真耗时约为4.5 s，波形符合预期。

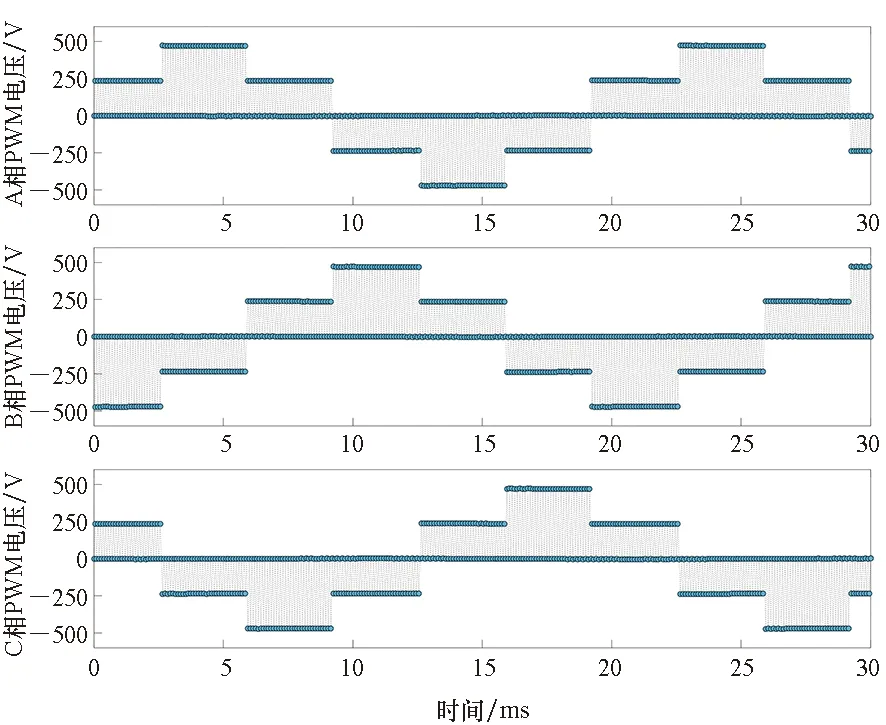
图3 模型无故障运行时的三相PWM电压数据Fig.3 Three-phase PWM voltage data when the model runs without fault

1.2 开路故障样本生成

电力电子逆变器通常为指定输出电压的电压源，根据其工作原理，当调制比、开关频率、基波频率等控制参数已确定时，逆变器输出的三相PWM电压波形也基本固定，使得与三相电流相比，三相PWM电压受负载变化的影响较小。在发生开路故障后，不同开路位置对三相PWM电压的影响也远远大于负载变化的影响，使得PWM电压能够清晰地反映开路故障信息。因此，本文利用三相PWM电压对负载变化不敏感的优势，将其采集为故障数据样本，用于CNN开路诊断模型的训练及测试。

将模型中不同的IGBT设置为常断开，即可模拟不同位置的开路(不同故障模式)并生成故障样本。单个故障样本包含两方面数据：①样本标签，即对应故障模式的编码；②对应故障模式下一定时长的三相PWM电压数据。该样本时长内各IGBT均受到多次开关驱动作用，由此组合成各种驱动状态并产生不同状态下的三相PWM电压数据， 它们共同提供可区分不同开路故障模式的故障特征。

1.2.1 故障模式分类及样本标签

考虑到多个IGBT同时发生开路故障的概率极小，因此仅对单管、双管故障进行研究，加上“无故障”共计有22种故障模式。为了便于编程和神经网络训练，根据IGBT编号顺序及开路情况将22种故障模式编码成如图4所示长度为6的布尔向量。

图4 三相两电平逆变器开路故障的编码规则Fig.4 Open-circuit fault coding rule of the three-phase two-level inverter

22种故障模式的标准编码如表1所示，即不同故障模式所对应样本的样本标签，将被用作CNN诊断模型训练时网络的标准输出。

表1 22种故障模式的样本标签

1.2.2 仿真样本生成及预处理

根据表1中各类故障模式，在图2所示模型中设置相应IGBT为常断开，随后仿真获取相应故障模式下的三相PWM电压样本。为了较好权衡诊断准确率与计算量之间的矛盾，设置采样频率为20 kHz，即4倍于5 kHz的开关频率(具体参见1.1节)。为了使样本具有一般性，设置每条样本的初始相位为随机。每种故障模式保存350个20 ms(单基波周期)样本，后续通过样本抽取及截断来分析样本时长、数量对CNN训练及诊断效果的影响。

对于单个样本，预处理时首先将三相数据序列并列组合为二维矩阵，以便于CNN对存在于三相电压局部差异中的大量故障细节信息进行卷积提取；然后，根据式(1)将矩阵元素归一化至[-1,1]范围，有利于避免网络权值过小和神经元饱和等数值问题、加速网络训练的收敛、提高网络在工况改变时的泛化能力。

(1)

其中，Dnor为对样本D进行归一化后得到的样本，|d|max为样本D中绝对值最大的元素。如图5所示，经上述预处理后，单个样本可被近似看作一幅像素为L×3的灰度图像，L为样本时长所对应的单相采样点数。

(a) 无故障(a) Normal

2 基于CNN的逆变器开路故障诊断方法

2.1 CNN诊断方法的建立流程

CNN及其他神经网络故障诊断方法的建立均参照图6所示流程，可大致分为网络训练和网络测试两个部分。首先将样本按一定比例分组为训练集、测试集。训练时，将训练集中的电压数据样本逐个输入搭建的神经网络，以网络输出与对应样本标签之间的误差最小化(损失函数值最小)为目标，对网络各连接权重及阈值进行迭代更新。网络被训练后，将测试集中的电压数据样本(对网络而言是未知样本)逐条输入网络，随后将输出归类到最接近的样本标签，对归类标签与样本实际标签进行对比分析，进而评估网络的诊断能力是否满足需求。若满足，即完成诊断模型的建立；若未满足，则对网络层数、神经元数、激活函数等超参数进行优化调整，并重复网络训练、测试流程。

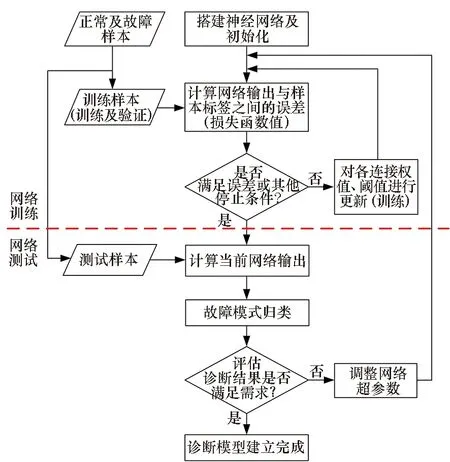
图6 神经网络故障诊断方法的建立流程Fig.6 Establishment process of neural network-based fault diagnosis methods

上述方法流程的目标是使网络能自动提取和利用样本的故障特征，进而形成由样本中的电压数据向样本标签映射的能力，实现故障诊断。

2.2 CNN构建及训练

基于BP网络或CNN的方法均遵循图6所示流程，并使用如图7(a)所示的同种M-P神经元模型，其区别主要体现在神经元不同的层间连接方式，如图7(b)、图7(c)所示。

单个M-P神经元的输入输出关系可表示为：

(2)

式中，f(·)为神经元的激活函数，wi为神经元第i个输入的连接权重，θ为神经元的阈值，这些权重和阈值即为网络的待训练权值。

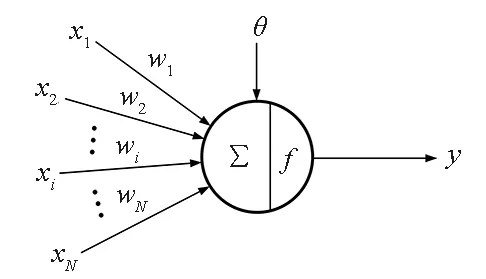
(a) M-P神经元模型(a) M-P neuron model

可以看出，对于图7(b)中BP网络的全连接结构而言，待训练的权值数量会随着网络层数、神经元数量的增加而大幅增加。CNN中则大量采用与如图7(c)所示的卷积层、池化层相配合的结构。卷积层中的每个神经元通过由卷积核(一组连接权值)构成的滤波器与前一层的局部区域连接，滤波器可视作按一定步长滑动从而提取不同区域的局部特征，即网络局部连接；可使用多个滤波器来加深信息提取的深度，但每个滤波器的卷积核保持不变，即卷积核权值共享。池化层中的元素一般取上一层的局部最大值或均值，可压缩神经元数量并增强网络的泛化能力。CNN的“网络局部连接”“卷积核权值共享”及池化层的使用，使网络可在大幅缩减待训练权值的条件下，对样本局部特征进行深度提取，并改善网络训练的“局部最优”及“过拟合”问题[21]。

由于三相PWM电压之间的相对差异是故障诊断的重要依据，因此自然做法是在某一算子支持下对三相数据进行逐段的局部对比，进而从局部差异中提取出大量的故障细节信息。这一过程符合CNN的“网络局部连接”“卷积核权值共享”特点，使CNN有望实现较好的诊断效果。对适合较小规模问题的LeNet-5网络模型进行了适应性优化，作为本文的CNN结构，同时建立BP网络用于对比，如表2所示。两种网络结构均是多次测试后的择优结果。

即先上后下，先高后低，先粗后细：（1）载物台的高度从上往下调节，可避免压碎载玻片；（2）物镜头转换先低倍镜后高倍镜，便于定位目标；（3）先用粗调节螺旋找到大致的焦点范围，再用细调节螺旋调节清晰的物像。

表2中的各隐藏层普遍采用ReLU激活函数，有利于加速训练收敛和改善“过拟合”问题[26]；输出层采用Sigmoid激活函数，促使网络输出较好逼近与样本标签相对应的0、1布尔值。CNN由卷积层、池化层完成局部特征提取后，仍使用全连接层来完成特征-样本标签映射，但其规模已远远小于BP网络中的全连接层，可有效避免权值过多问题。

表2 CNN与BP网络的主要结构参数对比

网络训练时，样本时长分别取2 ms，4 ms，…，20 ms，各故障模式的样本个数分别取20，40，…，300，以分析样本时长、训练样本数量对训练及诊断的影响；测试集中各故障模式取40个样本，用于评估诊断效果。网络训练采用自适应性优化器Adam[27]，损失函数为均方误差(mean square error，MSE)。此外，设置批训练样本量Batch Size为40，在本文条件下可取得较好的网络训练收敛速度及收敛稳定性；训练停止条件为“近5轮训练的损失函数不再下降”，可较好权衡欠拟合、过拟合问题。该CNN模型基于Python 3.8.5和TensorFlow-GPU 2.4.0深度学习框架搭建，使用便携式计算机的NVIDIA GeForce GTX 1050Ti GPU进行训练和推理。经测试，样本时长10 ms、各故障模式训练样本数为160时，上述CNN模型训练耗时约30 s，单样本推理耗时约0.14 ms。

图8对比了不同时长样本输入时CNN、BP网络的待训练权值数量，以及同条件多次训练中损失函数值的变化情况(样本时长10 ms、各故障模式训练样本数160)。可见，CNN在网络层数更多(深度更深)的情况下，其权值数量却远少于BP网络，例如当样本时长为20 ms时，BP网络的权值数量为256 766，而CNN的权值数量仅为40 822。训练中的损失函数值变化反映了训练过程收敛于全局最优解的趋势，可见CNN的收敛速度显著快于BP网络，且CNN可较稳定地收敛于较小的损失函数值，即CNN训练更容易接近全局最优解。

(a) 权值数量对比(a) Comparison of weight number

2.3 网络输出结果的故障模式归类器设计

将一个测试样本输入上述CNN、BP网络后，网络输出的6维向量处于(0,1)区间内，尚未与表1中的样本标签一一对应。为此，按式(3)对输出向量与各标签之间的欧氏距离进行计算，以距离最小作为判断标准将输出向量归类至对应标签，从而实现故障模式诊断。

(3)

式中，a1，a2，…，aN为输出向量A中的元素；b1，b2，…，bN为某一标签B中的元素。归类器在完成输出归类的同时，也使诊断过程具备了一定的容错能力。

完成上述CNN诊断模型训练及故障模式归类器设计后，单次诊断过程如图9所示(以1#IGBT开路为例)，主要包括三相PWM电压采集及归一化、CNN诊断模型推理、故障模式归类三个环节。

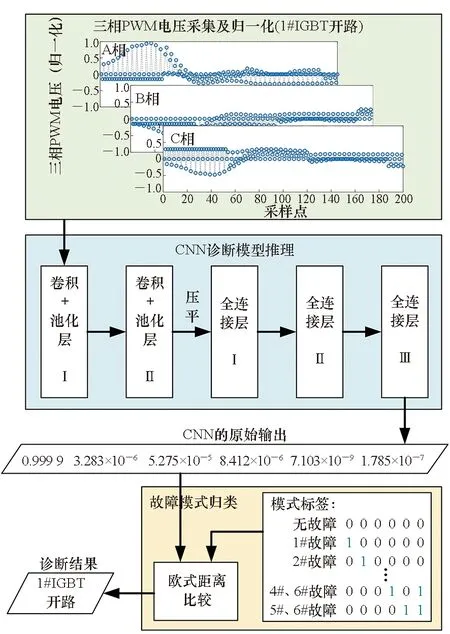
图9 单次开路故障诊断过程示例Fig.9 An example of open-circuit fault diagnosis

3 结果分析

在不同样本时长、训练样本数量条件下进行CNN、BP网络的训练及诊断测试对比。

3.1 评价指标

使用训练结束时的损失函数值Lfinal、诊断准确率Drate作为评价指标。Lfinal越小，表明训练使网络越准确地提取和利用了训练样本中的故障特征；Drate越高，表明训练后的网络对测试样本具有越强的诊断能力。

图10为某次训练后(样本时长10 ms、各故障模式训练样本数160)CNN、BP网络在测试集上的诊断结果分布图。

图10 CNN与BP网络在一次训练后的诊断结果分布Fig.10 Distribution of diagnosis results of CNN and BP network after a training

可以看出，在总计880个测试样本中，BP对17个样本诊断有误，CNN对3个样本诊断有误。根据诊断分布结果，由式(4)对诊断准确率进行计算。

(4)

式中，Nc为测试中被正确判断及定位的开路故障数量，Na为测试样本中的开路故障总数。在同一样本时长、训练样本数量条件下，后续均对网络进行多次训练，记录如图11所示的多个Lfinal和Drate(图中重复30次)，再计算均值以体现结果的一般性。可以看出，与BP网络相比，CNN在该条件下的Lfinal普遍较小、Drate普遍较高，且数值波动较小，表明CNN可更有效提取和利用训练样本中的故障特征，实现更准确且稳定的诊断。

(a) 30次训练及测试的Lfinal对比(a) Comparison of Lfinal in 30 training and diagnoses

3.2 不同样本时长下CNN与BP网络的结果对比

图12为各类故障模式的训练样本数为160，样本时长分别取2 ms，4 ms，…，20 ms时，CNN与BP网络Lfinal和Drate的变化趋势，图中每个数据点均为5次训练及测试后的平均结果。可以看出，Lfinal随样本时长的增加总体呈减小趋势，Drate则随样本时长的增加总体呈上升趋势，这表明增加样本长度总体有利于改善网络的训练及诊断效果，这是因为较长的样本中包含了更充分的故障信息。此外，CNN的Lfinal比BP网络整体较小、Drate整体较高，且随着样本时长的增加更快收敛至较优值，这意味着CNN方法可在样本较短(网络权值亦较少)时取得相同的诊断精度，实现更高的诊断效率。具体而言，CNN在样本时长为4 ms时就达到了99.21%的诊断准确率(文中诊断准确率的计算方法如式(4)所示)。

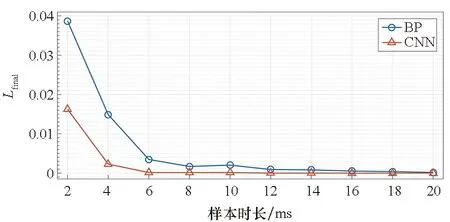
(a) 不同样本时长下的Lfinal对比(a) Comparison of Lfinal under different sample durations

3.3 不同训练样本数量下CNN与BP网络的结果对比

图13是样本时长为10 ms(半基波周期)，各故障模式的训练样本数分别取20，40，…，300时，CNN与BP网络Lfinal和Drate的变化趋势，图中每个数据点均为5次训练及测试后的平均结果。可以看出，Lfinal随训练样本数量的增加总体呈减小趋势，Drate则随训练样本数量的增加总体呈上升趋势，这表明增加训练样本数量有利于改善网络的训练及诊断效果，这是因为较多的训练样本可为网络训练提供更丰富和全面的故障信息。此外， CNN与BP网络相比，Lfinal整体较小、Drate整体较高，当训练样本数较少时优势十分显著，且随着训练样本数量的增加更快收敛至较优值，这意味着CNN方法可在明显较少样本的支持下得到相同的诊断精度，从而显著降低应用中对实际故障样本的积累要求并缩短网络训练时间。具体而言，CNN在各类故障模式的训练样本数量为40时就可达到99.82%的诊断准确率。

(a) 不同训练样本数量下的Lfinal对比(a) Comparison of Lfinal under different training sample numbers

4 结论

本文以电能变换装置开路故障的智能诊断需求为牵引，针对传统BP神经网络方法存在的“参数膨胀”“局部模糊”问题，研究了基于CNN的开路故障诊断方法，并以三相两电平逆变器为代表，着重开展了不同样本时长、训练样本数量条件下的方法仿真对比及验证。结果表明，利用CNN“网络局部连接”“卷积核权值共享”等特点，可建立比BP网络权值更少、深度更深的深度学习网络模型，使诊断网络具备权值少、训练收敛快、稳定性强、诊断准确率高等优势。对于本文的三相两电平逆变拓扑而言，当各类故障模式的训练样本数为160时，基于CNN的诊断方法仅需4 ms样本时长就达到99.21%的诊断准确率；当样本时长为10 ms时，各类故障模式只需40个训练样本就达到99.82%的诊断准确率。本文的样本条件分析过程及相关结果可为实际应用中合理确定样本条件，从而为提高神经网络诊断模型的训练及诊断效率提供有益参考。

下一步计划结合实验装置搭建，进行实机环境下充分考虑噪声、线路杂散参数、多类故障耦合等干扰因素的诊断方法优化，同时综合考虑AI终端硬件的计算能力、诊断准确率等因素，研究在线诊断时样本时长、采样率的最优选择策略，从而进一步提高方法的鲁棒性和工程适应性。