城镇智慧水务日用水量预测方法改进分析
2022-12-02孙小燕
孙小燕
(惠州市供水有限公司,广东 惠州 516001)
1 概 述
随着5G技术的发展,新基建应运而生,随之而来的是智慧城市建设。作为智慧城市建设中重要一环的智慧水务,通过与新一代的5G技术与水务技术深度融合,用以实现水务系统的精确化、智能化管理,保证水务系统有效、科学地运行,从而极大地节省人力成本。在实际生活中,要采用信息技术对水务供给系统实施全过程监控,其中重要的一环是对城市用水量进行精确的预测[1-5]。
为此,许多学者采用不同方法对城市用水量进行了预测。李琳[6]以郑州市为例,对城市用水量的预测方法进行总结,并采用灰色GM(1,1)模型及用水量定额法对郑州市用水量进行了预测,结果显示郑州市用水量总体呈现出非线性增长趋势。邹广宇[7]分析了城市用水量的影响因素,通过BP神经网络建立预测动态用水量的预测模型,并通过沈阳市用水量对模型进行验证,结果显示该模型误差较小。王圃[8]基于传统灰色模型的局限性,在无偏灰色GM(1,1)的模型之上,提出一种加权组合模型,并使用该模型与无偏灰色GM(1,1)模型与非线性模型进行自由组合,通过该种组合模型对遂宁市用水量进行预测,研究显示预测结果与实际效果吻合较好。严旭[9]采用GA遗传算法对传统BP神经网络预测模型进行了改进,结合深圳市用水量特点,得出合适的输入变量建立了预测模型,并对比深圳市的用水量验证了该模型的可靠性。
上述研究通过建立预测模型或算法对城市用水量进行了预测,并给予一定的验证。但实际上,用水量的变化特点具有一定的时变形和非线性,需要考虑到气温等诸多因素,而传统的预测模型或算法往往很难体现这一点。因此,本文基于5G智慧水务技术,以H市自来水公司2020年的数据为研究对象,在考虑不同影响因素的条件下,对LR、SVR、BPNN这3种算法进行评估、改进,并对改进后的算法进行对比分析。
2 项目技术概况
工信部〔2020〕25 号文件提出,建立 NB-IoT(窄带物联网)、4G(含 LTECat1)和 5G 协同发展的移动物联网综合生态体系,在深化 4G 网络覆盖、加快5G 网络建设的基础上,以 NB-IoT 满足大部分低速率场景需求,以 LTE-Cat1满足中等速率物联需求和话音需求,以 5G 技术满足更高速率、低时延联网需求。
在智慧水务项目实施过程中,很多应用场景基于 NB-IoT 实现物联感知和智慧应用,NB-IoT 是 5G 的先行者,将成为 5G 关键技术之一。当前 NB-IoT 在 R15 版本能够支持 NB-IoT 和 NR 空口共存,R16 版本支持 NB-IoT 接入 5G 核心网。根据 3GPP 自评估和中国独立评估结果,NB-IoT 满足 ITU mMTC 的要求,并已经通过 5G 候选提交,2020 年 7 月正式成为 ITU 5G 标准。
当前,业界已经认可 5G mMTC 的 LPWA 标准将基于 NB-IoT 平滑演进。因此,在当前智慧水务的网络基础设施建设中,必然会出现 NB-IoT 与 5G 网络融合的应用搭配。5G 作为第 5 代蜂窝网络,相比 4G 在峰值速率、网络容量、连接密度等网络性能方面有 10~100 倍的增强,其大宽带、低时延、大连接的特性,将在智慧水务领域掀起一波新的物联网应用浪潮。水务公司可以利用 5G 网络实现全方位、立体化的智慧水务管理,特别是水务管网巡视、水厂无人值守视频监控、VR 无人机安防等,而在远程抄表等领域继续采用 NB-IoT 平滑演进到 5G,从而兼顾更多更优的技术特征,丰富不同的应用场景。
3 研究方法
本文采用3种算法作为预测5G智慧水务用水量的基本预测研究算法,其中包括线性回归算法(LR算法)、支持向量回归算法(SVR算法)、神经网络学习算法(BPNN算法)。
3.1 LR算法
线性回归算法(LR)因其简单基础,是目前学界广泛采用预测用水量的机器学习算法之一。对于用水量的预测,其线性回归模型为:
Lθ(x)=θ0+θ1x1+θ2x2+…+θnxn
(1)
式中:Lθ(x)为预测用水量;x1,x2,…,xn为自变量影响因素;θ0为回归常数;θ1,…,θn为权重系数。
3.2 SVR算法
用水量预测采用支持向量回归算法(SVR)在支持向量机算法(SVM)的基础上,更加适用于此类回归分析。对于线性函数模型而言,通过在线性函数两侧设置间隔带,对落入间隔带内的样本不计入损失,以此来最小化总损失和最大化间隔带;而对于非线性函数则是通过核函数映射到线性空间之后,再进行回归分析。采用SVR算法对用水量进行预测,假设间隔带函数为:
f(x)=λTx+b
(2)
则利用该间隔带函数可得到SVR求解的模型为:
(3)
式中:m为日用水量数据;αi为拉格朗日乘子;κ(x,xi)为核函数;yi为第i个样本的实际日用水量;ε为允许误差。
3.3 BPNN算法
神经网络学习算法(BPNN)是目前最为常用的预测算法,由输入层、隐层、输出层构成,通过不同数量的神经元构成。采用BPNN算法对用水量进行预测时,需确定神经元数量和最大迭代次数,并通过神经网络的输出值与实际用水量的误差,不断更新连接权重。见图1。

图1 神经网络学习算法(BPNN)结构图
4 结果分析
4.1 用水量影响因素分析
本文以H市自来水公司2020年5月的用水量数据为例,将与方差相差较大的数据去除,并对该公司所在城市的用水量样本数据进行分析。城市用水量受诸多因素影响,但一般受温度、节假日、天气等因素影响较大。本文以5月份日期为横坐标,以用水量为左纵坐标,4种主要影响因素为右纵坐标,总结该公司所在城市5月份的用水量及影响因素,并绘制图2。图2中,0为工作日,1为节假日,天气情况为量化后的效果,具体参考见表1。

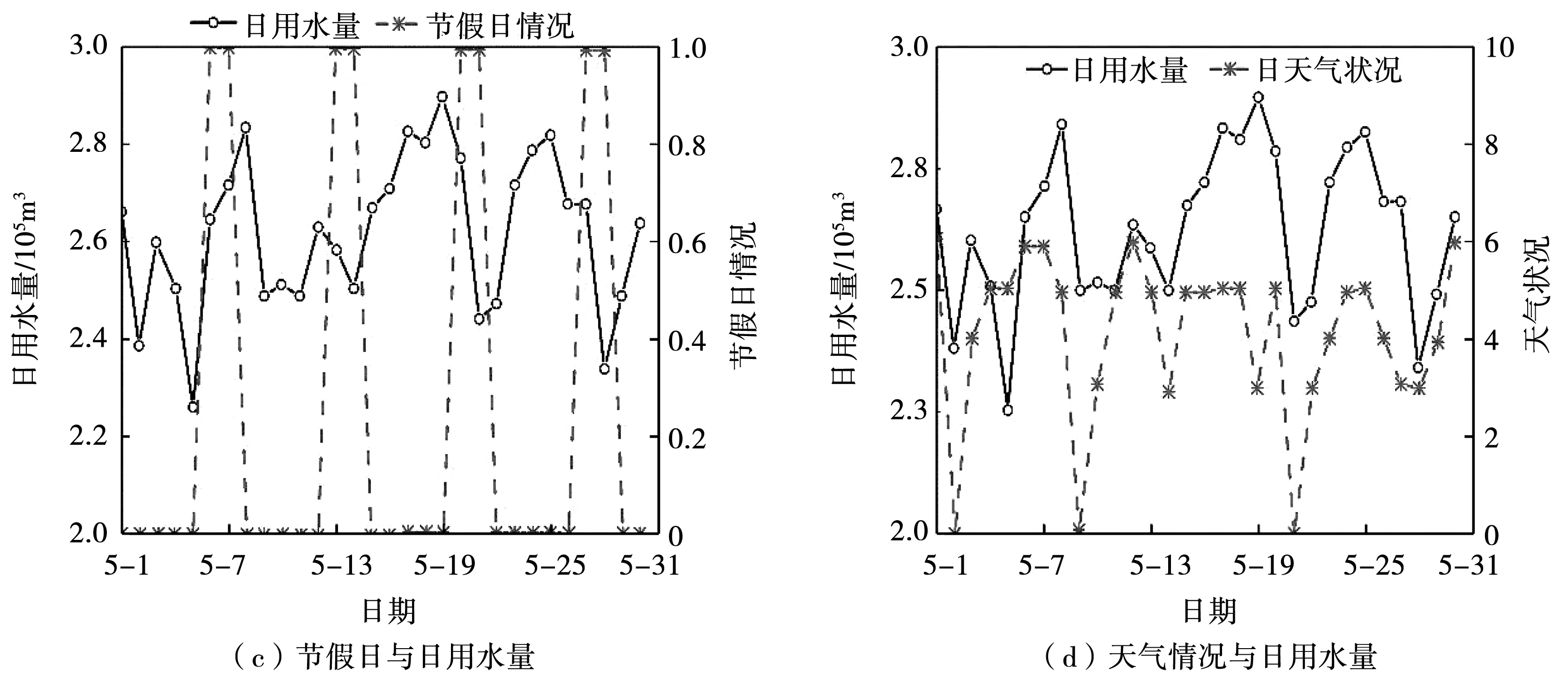
图2 H市5月份用水量随4种影响因素变化图

表1 天气情况量化数据表
图2(a)和图2(b)为最高气温与最低气温影响下的日用水量变化图。从图2(a)和图2(b)中可以看出,随着气温的升高,用水量也会随之升高,温度与用水量的变化呈现正相关。从图2(c)可以看出,在工作日与节假日时,日用水量并无较大变化,其原因在于本次统计的用水量数据包含工业用水,由于工业用水量的存在,在节假日时整体用水量不会出现太大变化。图2(d)为量化后的天气情况影响下的日用水量变化图,结合表1可以看出,天气较好时日用水量有上升趋势,但日用水量会随着天气转阴转雨而略有下降。
为了得出图2中4种影响因素与日用水量的相关性,通过具体数据求取二者的相关系数ρ:
式中:ρ为相关系数;COV为协方差;X为影响因素因素;Y为日用水量。
通过式(4)得到不同影响因素与日用水量的相关系数,见表2。

表2 4种影响因素与日用水量的相关系数
从表2中可以看出,气温与日用水量的相关性最大;其次为天气情况;节假日与日用水量的相关系数为负数,二者相关程度最低。
4.2 预测算法改进分析
分别采用LR、SVR、BPNN算法对H市自来水公司的数据进行预测。针对4个不同影响因素,通过建模与测试,对SVR算法的核函数选取RBF函数,并将函数中的参数C和g分别取值为3和0.016;对于BPNN算法则选取4个输入层,20个隐层和1个输出层。将此3种算法下输出的预测结果对比真实用水量,并进行预测误差的统计,3种算法的预测误差见表3。

表3 3种算法下的预测误差
可以看出,3种算法的预测误差偏大。为此,本文对3种预测算法进行了改进。在相关预测中,考虑到通过前一日用水量对整体用水量预测的重要性,本文统计了H市自来水公司前一日用水量和前8 h用水量的数据,见图3。
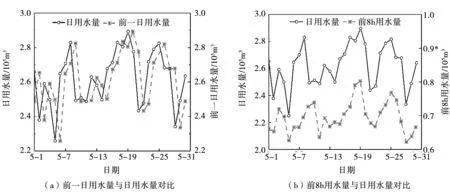
图3 前一日及前8 h用水量与日用水量对比
为了得到其相关程度的高低,同样采用式(4)计算其相关系数,见表4。

表4 前一日及前8h用水量与日用水量相关系数
通过上述计算分析可知,前一日用水量与前8h用水量均与日用水量相关程度较高,因此将此两种影响因素加入到预测算法之中,以便获得更小的误差。为了降低预测误差,对相关算法进行改进,对SVR算法的RBF核函数关键参数C和g分别设置为68和0.01;BPNN算法的输入层神经元改为6个,隐层神经元及输出层神经元数目均不变,分别设置50个测试集对相同的数据进行预测,计算相关算法的预测误差,并与改进前算法的预测误差进行对比,结果见图4。
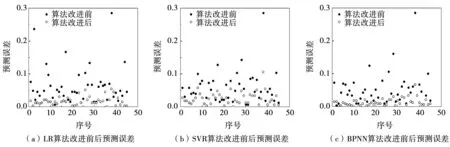
图4 3种算法改进前后的预测误差
从图4中可以看出,对比改进前算法,在算法改进后误差分布相对集中,整体误差均处于0.1以下,说明改进后的算法具备更好的预测效果。对比不同的算法可以看出,随着测试集的变化,BPNN算法波动程度较小,对于测试集内的预测效果最好;而SVR算法波动程度最大,稳定性较差。
由于气温对日用水量的相关程度最高,因此为了得到改进后算法在不同气温下的预测效果,本文对5月份进行了划分,1-14日为a组,15-31日为b组,SVR和BPNN主要参数设置均不变,设置30个测试集对预测误差进行测试,见图5。
从图5中可以看出,改进后的LR算法和BPNN算法在不同温度下,预测误差较为集中,说明在不同温度下此二种算法依然可以保持较高的预测精度;但对于SVR算法,温度的变化会引起其预测误差随之发生改变,温度变高或者变低时,其预测精度会随之下降,但这种情况随着测试集的增加而减小。

图5 改进后的3种算法在不同温度下的预测误差
5 结 论
本文基于5G智慧水务技术,以H市自来水公司2020年的数据为研究对象,在考虑温度、节假日、天气情况等影响因素的条件下,对LR、SVR、BPNN这3种算法进行评估、改进,并对改进后的算法误差进行对比分析,结论如下:
1) 通过改进SVR、BPNN算法的主要参数,改进后算法的预测精度明显较改进前有进一步提高。
2) LR、BPNN算法受测试集与温度影响较小,但SVR算法受温度影响较大,高温或低温均会减小其预测精度,通过增加测试集可以降低此类情况。建议在一般情况下,采用改进后LR、BPNN算法;在测试比例较大时,可以采用SVR算法进行用水量的预测。
