基于希尔伯特-黄变换的直流线路故障测距研究
2022-12-02李延
李 延
(中电建武汉铁塔有限公司,湖北 武汉 430000)
0 引 言
随着“双碳”战略日益推进,清洁能源在能源网络中的大幅流动逐渐占据主导。在跨区和跨网的能量调度中,高压直流输电工程发挥着极其重要的作用。高压直流输电工程是提高电网稳定性的重要途径,也是坚强智能电网的重要组成部分。受制于成本条件,当前的直流输电线路仍然大多使用架空线路输电方式。由于我国复杂的地形条件和多变的气候条件,直流架空线路在自然环境下受到极大威胁[1,2]。此外,长距离的输电线路也使故障率大大提高。以上问题不仅是输电线路脆弱的主要原因,也是直流线路故障发生后巡检和检修工作的难点[3,4]。恶劣的自然环境和远距离输电使工作人员难以定位直流输电线路的故障点,并且人工巡查的方式效率低下,增加了人工成本。针对故障发生后难以及时定位的问题,需要通过对故障生成的物理特性进行分析来帮助工作人员快速定位并修复故障[5,6]。
当前对直流输电导线故障定位已有不少成果,其中小波变换法的研究时间较长,技术较为成熟[7,8]。文献[9]提出了直流架空线路故障测距模型及其基于优化小波重构算法的直流输电线路故障行波测距方法,但基于小波变换的原理,算法要求选择合适的小波基以及对应的分解尺度,故该方法自适应能力较差。文献[10]通过信号突变时刻蕴含的信号特征进行故障定位,利用数学形态学梯度技术分析暂态行波。该方法可以精准定位故障,尤其在高阻抗接地等故障定位中有良好表现。但方法需要确定结构元素的尺寸和形状,考虑因素较多。彭楠等人提出了适应半波长输电线路的分布式行波测距方案,方案中分析了两端行波故障测距关于波头的色散畸变性的影响程度[11]。利用小波Teager能量算子得到线路两端收到行波的时刻,进一步得到故障精确定位,同时解决了测点数据丢失的问题。以上研究在直流线路故障测距方面有较好的运用,但缺乏一种检测快速且适应性广的方法。
针对以上问题,使用希尔伯特-黄变换对直流输电线路产生的故障信号进行分析。通过分析故障波头信号并综合直流输电线路的相关参数,配合双端故障测距法来定位线路上的故障点。
1 直流输电线路行波故障测距
在直流线路发生接地故障时,故障点的瞬时电压下降至零。在短路瞬间等效于在故障处并入一个电压源,该电压源的幅值与故障时,故障点处的电压幅值相关并且极性相反,故障点处的电压突变信号由故障点为中心向直流输电线路两端扩散。
当由故障引起行波的传播时,传统的行波故障定位通过线路两侧的检测装置记录行波到达时间,基于时间来测算故障距离,D型行波测距方法是其常用的距离计算方法。D型双端测距原理如图1所示。
其基本原理为
式中:TM和TN为线路两端检测点记录的波头到达时刻;v则为行波在线路上传播的速度;LMF、LNF分别为故障点到M、N端的长度;L为整条线路的长度。
将式(1)以双端距离形式表示为
由式(2)可知,D型双端测距法的未知量只有TM、TN。实际的故障情况需要考虑到实际直流输电线路的特殊情况,使用D型双端测距法并不能对故障点进行精确定位。
由于上述方法的局限性,需要另外一种不受波速影响的双端测距算法。不受波速影响的行波反射算法原理如图2所示。
该方法不仅需要初始波头到达线路两端监测点的时间,还通过引入故障点的反射波再次到达M端的时刻来精确波速,以此达到精准定位故障点的目的。
根据测距原理可以得到
由式(3)化简得
式中:x为故障点到线路M端的距离;t1、t2、t3分别为波头到达M、N端时刻和反射波波头到达M端时刻;l为线路总长。但此方法难点在于反射波到达M端的时刻t3难以通过测量获取。基于以上方法,为改进其局限性,采用一种改进的双端故障测距方法。其原理如图3所示。
由测距方法可得
由式(5)可得故障距离定位为
式中:R、L分别代表直流输电线路两端检测点,即整流端和逆变端;XR、X1分别为故障点到R、L两端的距离;t、tR和t1分别代表故障发生时刻和行波到R、L端记录的时刻;vR、v1分别为通过计算得到的故障波头在两端的波速度;L为线路总长。
2 希尔伯特-黄变换
经验模态分解(Empirical Mode Decomposition,EMD)和希尔波特(Hilbert)变换是希尔伯特-黄变换的主要过程。EMD分解的通过分析原故障行波信号并且分解成各固有模态函数(Intrinsic Mode Function,IMF)分量,其分解出的信号IMF根据信号频率降序生成。EMD分解的目的是提取特征量,得到在不同时间段内的单频率成分固有模态函数分量。固有模态函数分量可表示信号中蕴含的频率特征信息,其是由被分析信号的各特征尺度信息分量组合构成。分解得到的固有模态函数按分解层数的增加特征尺度梯度增加,瞬时频率降序排列。
希尔伯特-黄变换流程如下文所述。
(1)输入行波信号,并找到信号最大最小值点;
(2)绘制最大最小值包络线,并求出包络线均值;
(3)用原信号和包络线平均值得到疑似IMF分量;
(4)判断IMF分量,若均值线的平均值趋近于零,原信号极值点个数和原信号与x轴交点个数差不大于1,则将原信号减去当前IMF分量作为新信号回到步骤(1),否则将IMF信号作为原信号回到步骤(1);
(5)将满足条件的固有模态函数进行希尔伯特变换,得到时频关系图。
2.1 瞬时频率
瞬时频率表示为故障出现时直流输电线路上的频率。对于输入的c(t)原信号的希尔伯特-黄变化有如下处理过程。
正变换为
反变换为
式中:PV代表柯西主值;t表示时间。X(t)与Y(t)互为复共轭关系,由两者可得新时间序列Z(t),即
式 中:a(t)、θ(t)分别表示瞬时幅值和相位。。则瞬时频率计算公式为
2.2 基于希尔伯特-黄变换算法的故障信息计算
直流电流信号在故障发生时,会出现电流信号的突变,获取该信号是故障测距的关键之处。通过EMD分解可以得到频率增长式分布的IMF分量,这些分量会进入希尔伯特变换进行高频故障信息的提取。因突变时信号幅值变化最为剧烈,故选取故障信号最明显和包含信息最多的IMF1作为故障分析的目标分量。
2.3 行波速度计算
某频率分量的传播速度为
式中:ω为该分量的角频率。β(ω)的计算公式为
式中:β(ω)为该分量的相位畸变系数;r0、g0、L0、C0分别表示直流输电线路的单位电阻、电导、电感、和电容值。
3 仿真及分析
本文建立了如图4所示的高压直流输电系统,仿真使用PSCAD电磁暂态软件,模型参考CIGRE标准模型和其参数。设定直流输电线路的输送容量为80 MW,线路额定电压等级设定为110 kV,线路长度设定为200 km。直流输电线路参数如表1所示。

表1 直流输电线路参数
仿真设置故障发生时间在2 s处并且故障发生点设定在距离线路中间,即距离整流段100 km处,并且过渡电阻值为0 Ω。经过希尔伯特-黄变换得到了整流侧的瞬时频率为1 278 Hz,对应的逆变侧的瞬时频率为846 Hz。由上节所推导的公式可以得到故障行波波头被两端记录时的波速度。波头到达整流侧时波速度为2.821×108m·s-1,而逆变侧计算的波速度为2.819×108m·s-1。计算可得估计的故障点距离为离整流端100.51 m处。图5为整流侧得到的故障电流波形。
仿真结果如表2、表3、表4 所示。
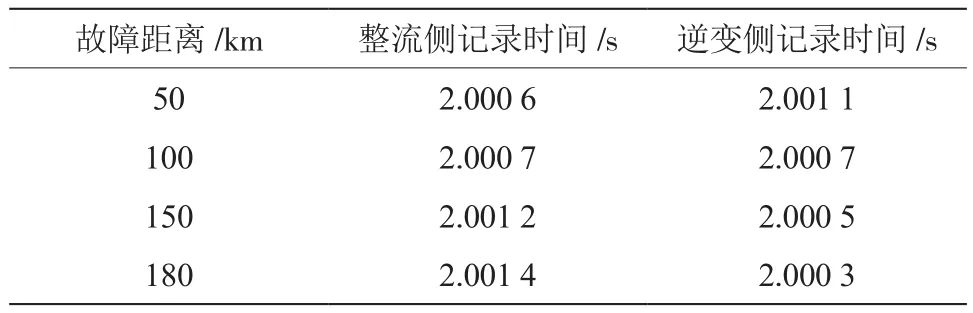
表2 不同故障点行波波头到达线路两端时间
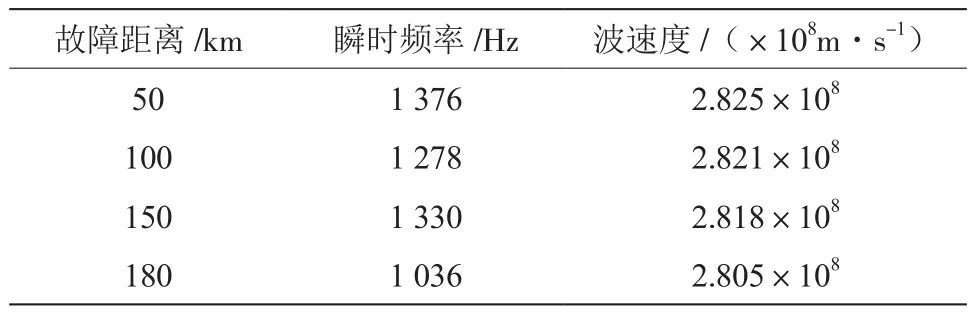
表3 不同故障点下瞬时频率和到达整流侧波速度
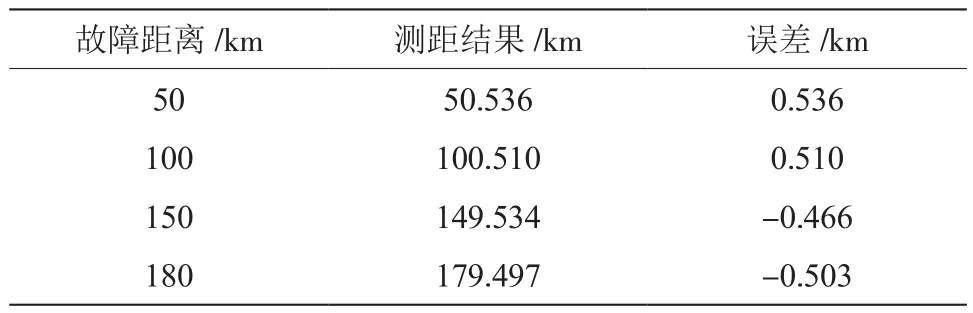
表4 双端测距结果
结果表明,使用希尔伯特-黄变换能够有效地对直流输电线路的故障点进行定位,保证了定位精度,方法适应性广。
4 结 论
通过希尔伯特-黄变换能够准确定位直流输电线路的故障发生点,且方法不通过以往波速度的经验值。通过故障信号变换后的信息可计算出实际的波速度。同时,不需要测量反射波波头信号来进行测距,使得方法具有更广泛的适应性。
