考虑新能源不确定性边界的主动配电网优化调度
2022-12-01虎智峰张婧菲李春科
虎智峰,陈 静,张婧菲,李春科,邴 骞,成 柯
(1.国网甘肃省电力公司临夏供电公司,甘肃临夏 731199;2.武汉大学电气与自动化学院,湖北武汉 430072)
0 引言
我国“碳中和碳达峰”发展方针和能源结构转型战略的提出,大大地推动了风电、光伏等间歇性新能源电源的发展[1]。然而,由于风电、光伏等分布式新能源出力受天气因素影响较大而呈现出较强的不确定性[2],高比例新能源发电电源接入配电网将给原有配电网优化调度体系带来挑战。因此,亟需探讨考虑大规模间歇性新能源接入下的主动配电网(Active Distribution Network,ADN)优化调度方法。
目前促进新能源在主动配电网消纳的方法主要包括储能[3]、负荷响应[4]、多种灵活性资源[5]、多时间尺度[6]等技术手段。虽然文献[3-6]技术方法在一定程度上可以促进可再生能源的消纳,但均为对新能源发电出力随机性、不确定性建模,因此无法从根本上抑制新能源不确定性所带来的不良影响。
当前,针对ADN 间歇性新能源发电建模的方法大致可以分为两大类:随机场景模型和鲁棒模型[7]。文献[8]通过高斯混合模型对间歇性新能源发电的不确定性建模,建立了含海量新能源随机场景的交直流ADN 优化调度模型。文献[9]以随机场景定义新能源发电功率,构建考虑新能源不确定性的直流配电网日前随机优化调度模型。为了求解大规模随机优化调度模型,文献[10-11]通过Galerkin 方法获得近似值函数,提出了改进的近似动态规划将大规模复杂随机优化模型分解为多个小子问题解决。文献[8-11]均通过随机场景的方式代表新能源不确定性,但为了充分考虑其对ADN 优化调度的影响,往往需要海量的随机场景,给模型求解带来极大地困难。与之相比,ADN 鲁棒调度方法通过区间的方法表征新能源不确定性,无需海量的随机场景[12]。文献[13-14]以不确定集合的形式刻画新能源不确定性,构建了基于多面体不确定集的ADN 优化模型,并通过Benders 或者列和约束生成算法求解所建模型。文献[15]为了获得更加精确的极端新能源波动场景,进一步提出了离散不确定集合的建模思路。文献[16]和文献[17]分别将配电网鲁棒优化方法扩展到充换储一体站和含热电联产机组新型城镇配电网中。文献[13-17]所采用的鲁棒优化框架可以有效地避免新能源场景过多的问题,然而仅仅针对新能源波动最恶劣的场景进行优化,而最恶劣场景在实际中发生的概率极低,因此所得鲁棒调度方案难免过于保守。此外,新能源不确定的边界都是人为确定,故新能源不确定边界的确定方法较为主观,无法客观确定。
针对现有ADN 优化调度方法中存在的问题,本文提出了一种基于最优新能源不确定边界的ADN 优化调度方法。首先,在新能源时序发电特性基础上构建了风险评估模型,评估ADN 优化调度方案可消纳的新能源不确定边界以及边界之外的潜在期望弃新能源和切负荷风险。其次,为优化配电网调度计划可以应对的最优新能源不确定边界,提出计及最优新能源不确定边界的ADN 优化调度模型,以合理地权衡发电调度成本与风险成本,设计了一种改进粒子群优化算法与分支定界算法相融合的双层混合优化算法求解所建含变限积分的混合整数非线性规划模型。最后,通过验证所提方法的有效性和优越性。
1 新能源不确定性建模
1.1 新能源发电特性分析
本文以我国西北某省的某风电场和某光伏电站为例分析其发电功率特性,其8 760 h 的功率曲线如图1 所示。由于光伏发电功率与太阳辐射强度密切相关,而每天均有一半时间处于光照强度较弱或者黑暗时段,故其出力集中在零功率附近。相比之下,由于风速波动性更大,而风力发电功率主要与风速相关,因此风电功率相较于光伏功率波动更大。在进行配电网优化调度时,需要对新能源不确定性进行合理建模,以充分应对其不确定性所带来的不良影响。
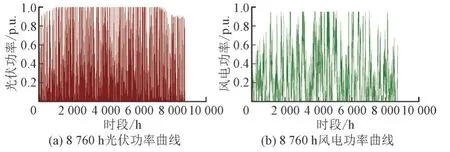
图1 我国甘肃地区某新能源基地一年功率曲线Fig.1 Power curve of renewable energy in Gansu province
1.2 基于预测概率分布的潜在风险评估模型
根据现有新能源预测技术和统计学规律[18],新能源预测误差服从以新能源预测出力为期望值、以为标准差的高斯分布,可表示为:

式中:为新能源预测误差分布函数;为新能源机组在t运行时刻的实际出力;Pr,max为新能源的装机容量;k为新能源预测误差系数,其取值主要取决于新能源预测技术,其数值大小通常为0.1—0.3。
对于短期新能源预测[19-21],其误差系数可取值为0.2。依据式(2)得到,新能源预测误差的标准差与新能源预测值及其装机容量Pr,max呈现正相关性。
新能源预测概率模型[22]如图2。其中,为新能源不确定性的最小值,为新能源不确定性的最大值,为ADN 运行方案可以应对的新能源不确定性下边界,为ADN 运行方案可以应对的新能源不确定性上边界。当新能源出力向上波动值越过可以接纳的上边界时,则ADN 调度方案由于无法消纳过多新能源功率而产生弃新能源风险;当新能源出力向下波动值超出可以接纳的下边界时,则ADN 调度方案由于无法消纳过多新能源功率而产生切负荷风险[23]。
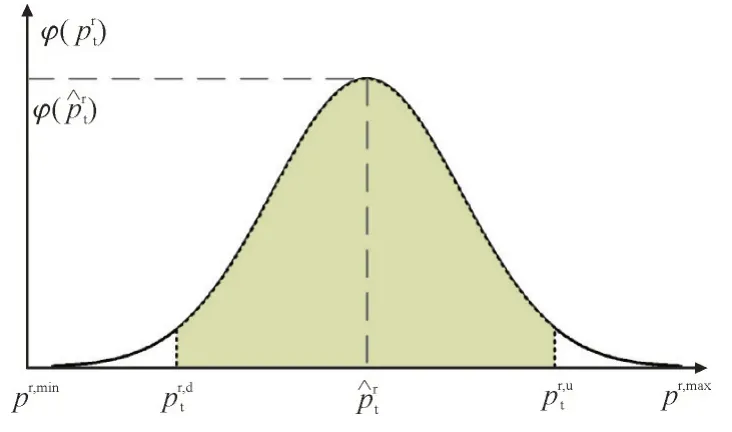
图2 新能源预测误差概率分布图Fig.2 Probability distribution diagram of renewable energy prediction error
因此,期望弃新能源电量风险可表示为:

2 计及最优新能源不确定边界的主动配电网优化调度模型
配电网调度计划所提供的可控灵活性成本与配电网所能应对的新能源不确定性边界风险具有矛盾性,为此,本文建立了计及最优新能源不确定边界的ADN 优化调度模型,以确定新能源不确定边界。
2.1 主动配电网结构框架
本文以典型含新能源的ADN 框架进行建模分析,如图3 所示,主要包括5 部分:上级电网(主网),以光伏机组和风电机组为代表的新能源发电机组,以燃气轮机(Gas Turbine,GT)、燃料电池组(Fuel Cell,FC)和蓄电池为主的传统机组,工业、商业和居民用电负荷,以及ADN 调度控制中心。本文所建立的ADN 调度优化模型旨在通过合理安排可控电源出力计划,以充分应对不可控电源的不确定性。

图3 含新能源并网的配电网框架Fig.3 Distribution network framework with renewable energy
2.2 目标函数
为了寻找ADN 调度计划可以应对的最优新能源不确定边界,本文提出了计及最优新能源不确定边界的ADN 优化调度模型,其目标在于使得发电调度费用fO与风险成本fR的总和最小,其中fR包括潜在期望弃新能源成本和切负荷成本,可表示如下:


本文将弃新能源和切负荷的惩罚系数取为25 元/kWh 和50 元/kWh。
2.3 约束条件
配电系统中包括GT,FC、蓄电池、上级电网等配网组件约束以及ADN 系统约束。
1)燃气轮机:GT 约束主要包括GT 发电出力区间限制约束、爬坡灵活性约束、最小启动约束、最小停机约束,具体可参考文献[9],其灵活性容量提供约束可表示为:
2)燃料电池组:FC 约束与GT 相似,在此不再赘述,其灵活性容量提供约束可表示为:

3)蓄电池:蓄电池约束主要包括蓄电池充电功率区间限制约束、放电功率区间限制约束、充放电功率互斥约束、剩余电量与充放电功率等式约束、电量容量上下限约束、蓄电池始末时段电量约束,具体可参考文献[9],其灵活性容量提供约束可表示为:
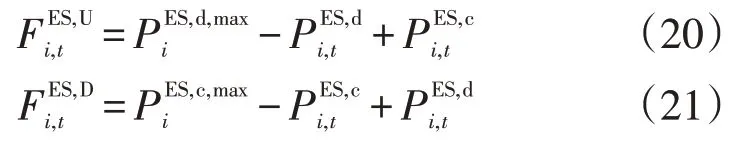

4)上级电网:上级电网与ADN 的联络线存在最大传输功率需满足功率约束:

式中:为ADN 节点i向上级电网购电功率的最大值为ADN 节点i向上级电网在运行时刻t的购电功率。
5)静止无功补偿器:静止无功补偿器是ADN系统中产生无功的重要方式,其功率调整对ADN无功优化具有重要意义,需满足无功上下限约束:

6)配电网系统:ADN 中的每个节点注入功率可以表示为:

ADN 系统的线路潮流的二阶锥形式可表示为:

式中:Pij,t,Qij,t分别为ADN 节点i到节点j在运行时刻t的有功功率和无功功率;κ(i)为ADN 中以节点i为子节点的节点集合;π(i)为ADN 中以节点i为母节点的节点集合;rij为ADN 线路ij的电阻;xij为ADN 线路ij的电抗;Ui,t为ADN 节点i在运行时刻t的电压;Iij,t为流经ADN 线路ij在运行时刻t的电流。
ADN 系统调度计划的总灵活性可表示为:

3 双层混合优化求解算法
文中所建立的风险成本式(3)和式(5)为变限积分项,目前尚没有高效的通用求解算法。为此,本文提出一种双层混合优化求解算法,以求解所建考虑新能源不确定性边界模型。

因此,上层模型为混合整数二阶锥规划问题[24],可以通过Cplex 求解器高效地求解。在求解上层模型后,可得到ADN 发电调度计划和ADN 发电调度成本fO*。下层模型为在ADN 发电调度计划和ADN 发电调度成本fO*给定前提下,寻找最小化发电调度成本fO*与风险成本fR之和,总调度成本F可表示为

同时,为了改进现有经典粒子群算法中所存在的收敛性慢和容易陷入局部最优解问题[20],本文进一步提出了基于可自适应变化惯性因子的改进粒子群优化算法,以在前期快速搜索全局解,同时提高后期收敛性能。

通过本文所采用的可自适应变化惯性因子改进策略,有效地兼顾算法的全局搜索性能和收敛性能,具体求解流程图如图4 所示。

图4 粒子群算法与分支定界算法相融合的双层优化流程Fig.4 Bi-level optimization process combining particle swarm optimization algorithm and branch and bound algorithm
目前已有的粒子群优化算法通常以最大迭代次数作为收敛条件。为了减少非必要的寻优迭代,本文以最大迭代次数和连续X次迭代的最优粒子适应度差值小于足够小的阈值α作为下层粒子群算法优化过程中的收敛条件。当算法未达到最大迭代次数但连续X次迭代的最优粒子适应度差值小于阈值α时,可认为其已达到算法收敛条件,此时将停止继续迭代。在本文中,为了使算法充分寻优,最大迭代次数设置为200 次,X取为10,阈值设置为0.000 1。
4 算例分析
为了验证所提模型的有效性和优越性,本文在MATLAB 软件中编程,上层混合整数二阶锥规划模型通过Cplex 求解器中的分支定界算法有效求解,下层期望风险成本模型通过改进粒子群算法求解,最后上层模型与下层模型相互迭代,最终得到ADN优化调度模型最优解。模型编程计算机环境型号为ThinkPad E14,内存容量为16 GB,内存频率为3200MHz,CPU型号为i7-1165G7,基准频率为2.8GHz。
4.1 算例系统简述
以IEEE 33 节点ADN 系统为例,验证所提ADN 优化调度方法的有效性和优越性。本文对原有的IEEE 33 配电网系统进行修正,增加了风电、光伏、GT、FC、蓄电池机组类型,如图5 所示。
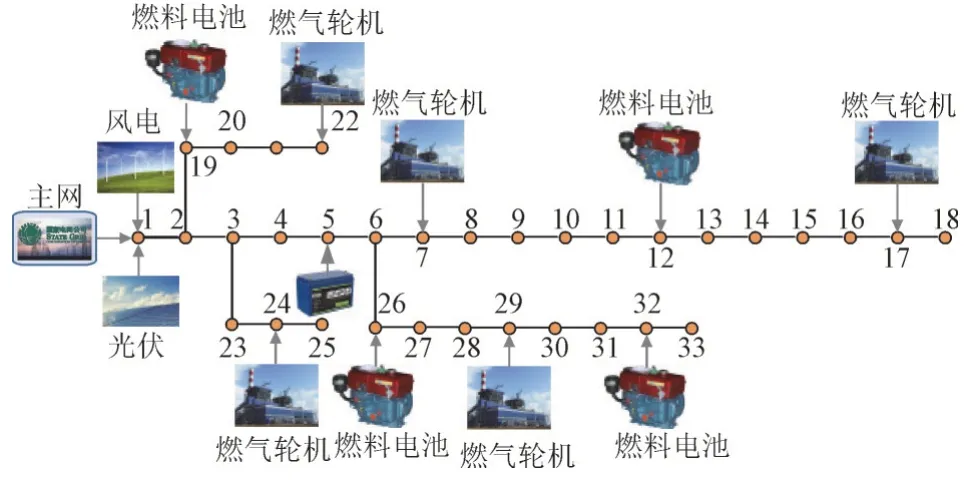
图5 修正后的IEEE 33节点配电网系统Fig.5 Modified IEEE 33 bus distribution network system
修正后的ADN 系统包含5 台微型GT,4 台FC,1 台风电机组,1 排光伏列阵和1 台蓄电池,其中GT 的功率容量为70 kW,爬坡速率为120 kW/h,FC 的功率容量为80 kW,爬坡速率为150 kW/h。风电机组和光伏列阵的装机容量均为350 kW。
4.2 不同新能源不确定性边界下的调度方案对比
为了充分展示新能源不确定边界对ADN 调度计划的影响,本文分别取10%,20%,30%,40%,50%,60%和70%的新能源不确定性,并测试相应调度方案的发电调度成本、风险成本和总调度成本,其结果如表1 所示。
表1 结果显示,随着新能源不确定性边界从10%增加至70%,发电调度成本逐步增加,风险成本逐步减小,总成本先减少后增加。对于发电调度成本而言,随着可应对新能源不确定性边界的增加,ADN 调度方案需用于应对新能源不确定性和波动性的备用容量增加,从而增加ADN 调度方案的发电调度成本。对于风险成本而言,随着可应对的新能源不确定性边界增加,此时ADN 调度方案可应对的新能源不确定性能力增加,因此调度方案所面临的期望弃新能源和切负荷风险减小。对于总成本而言,由于在新能源波动较小时,风险成本占据主导位置,因此总成本随着边界的增大而降低。而当ADN 调度方案可应对的不确定边界增大到一定程度时,此时发电备用成本的增加占据主要位置,总成本随着边界的继续增大而增加。因此,ADN 调度方案的总成本随着新能源不确定性边界的增大先减小后增加。
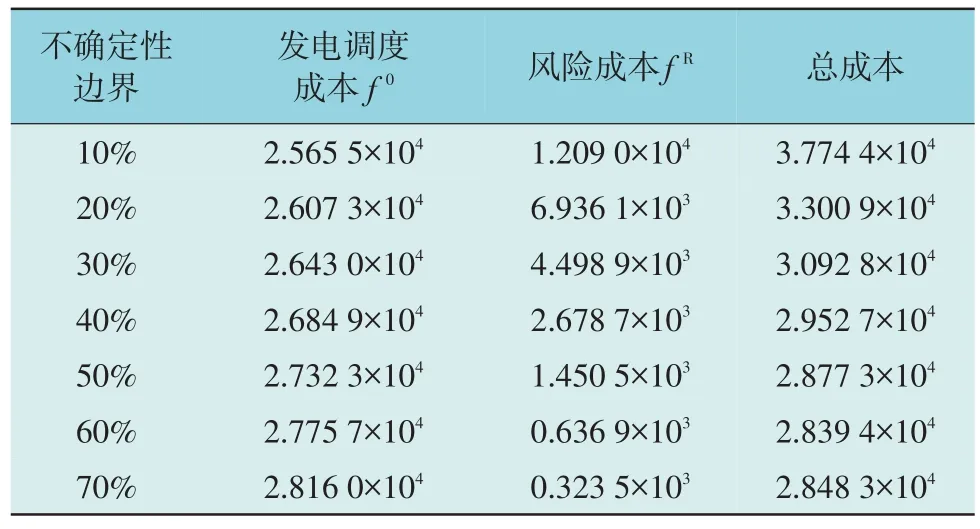
表1 新能源不确定性边界对主动配电网调度方案影响Table 1 Influence of uncertain boundary of renewable energy on active distribution network dispatch scheme 元
4.3 不同配电网调度方法的对比
为了验证所提ADN 调度方法的有效性和优越性,本文将所提考虑新能源不确定性边界的ADN优化调度模型与现有文献中的确定性优化调度方法[5]、鲁棒优化调度方法[15]对比,其发电调度成本、风险成本和总成本结果如表2 所示,GT 和FC 出力对比结果分别如图6、图7 所示。
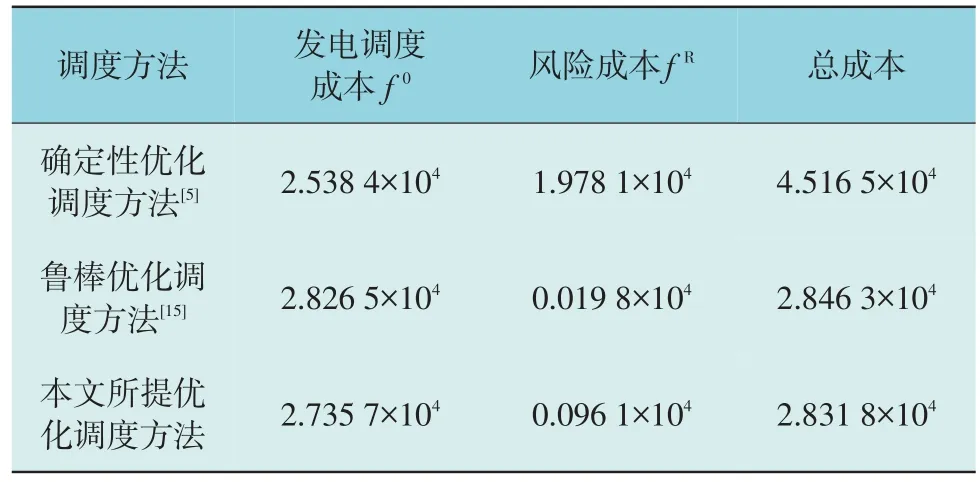
表2 不同配电网调度方法的对比Table 2 Comparison of different distribution network dispatching methods 元
综合表2、图6 和图7 可知,在3 种ADN 优化调度方法中,确定性优化调度方法虽然可以让GT,FC 等可控发电机组处于经济性最好的发电状态,发电调度成本最低,然而由于其忽略新能源不确定性,调度方案存在极大的潜在期望弃新能源和切负荷风险,因此其总成本最高。

图6 燃气轮机出力对比Fig.6 Comparison of gas turbine outputs
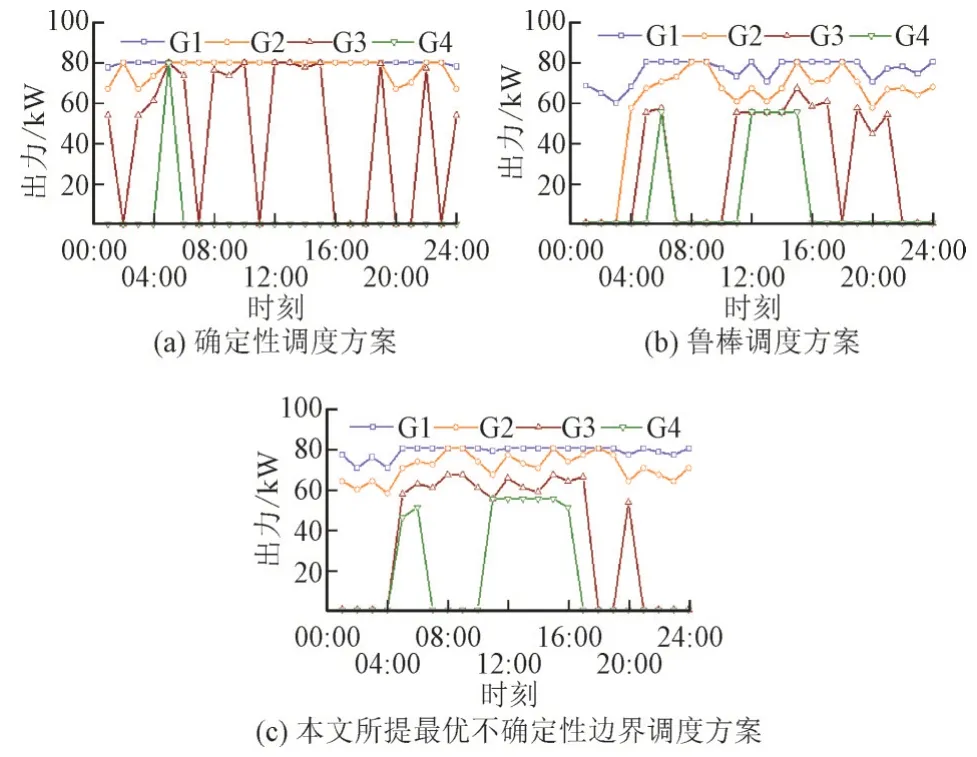
图7 燃料电池组出力对比Fig.7 Comparison of fuel cell outputs
鲁棒优化调度方法虽然充分考虑新能源不确定性对调度决策的影响,潜在风险较小,但由于其过多地关注几乎不会发生的极端恶劣新能源波动场景,因此需要调整GT,FC 等可控发电机组的出力以预留足够的备用容量应对极端新能源波动场景,容易造成备用容量的浪费,导致其发电调度成本和总成本均较高。
相比之下,本文所提的基于新能源不确定性边界的ADN 优化调度方法可以灵活地寻找最优新能源不确定性边界,合理地权衡发电调度成本与潜在期望风险成本的矛盾关系,以达到调度方案的总成本最优。
4.4 求解算法对比
为了验证所提基于可自适应变化惯性因子的改进粒子群优化算法的有效性,本文将所提改进算法与经典粒子群优化算法[20]对比,其求解时间、迭代次数和最优解的对比如表3 所示。

表3 算法结果对比Table 3 Comparison of algorithm results
由表3 可知,与经典粒子群优化算法相比,本文所提的基于可自适应变化惯性因子的改进粒子群优化算法可以快速收敛,迭代次数减少了33 次,所需的相应求解时间减少了264 s。同时,本文所提的自适应变化惯性因子改进机制有助于跳出局部最优解,增强全局搜索性能,可获得更优的最优解。
5 结论
本文提出了考虑新能源不确定性边界的ADN优化调度方法以及基于改进粒子群算法与分支定界算法的双层混合求解算法,通过算例分析,得到了以下结论:
1)随着可应对新能源不确定性边界的增大,发电调度成本逐步增加,风险成本逐步减小,总成本先减小后增加。
2)与现有ADN 确定性经济调度和鲁棒经济调度方法相比,本文所提最优新能源不确定性边界方法在经济性上更优,有效地兼顾调度方案的运行成本性能和潜在期望风险。
3)与现有粒子群优化算法相比,本文所提粒子群优化算法能获得更优解,同时迭代求解速度更快。
