时变风险厌恶与黄金期货市场波动率——基于GARCH-MIDAS模型的实证研究

吴鑫育, 张 静

(安徽财经大学 金融学院, 安徽 蚌埠 233000)

一、 引 言

世界政治、经济的不确定性使得全球经济产生巨大震荡,国际股票市场、债券市场及大宗商品市场普遍受到了不同程度的冲击。在这种经济衰退背景下,贵金属市场却没有过多受到影响,仍处于平稳增长状态。其中黄金作为全球储备货币和套期保值重要组成部分,与其他贵金属相比具有明显优势和突出地位,在社会经济发展过程中的作用不言而喻。

Mensi等[1]的研究表明贵金属与股市之间存在波动溢出效应,四大贵金属市场(金、银、钯、铂)是全球金融危机和欧洲主权债务危机期间波动性溢出的净接收方。鉴于此,黄金期货作为减缓经济政治冲击和管理黄金价格风险的最佳工具引起了众多学者和投资者的兴趣。Fang等[2]将全球经济政策不确定性指数(GEPU)引入GARCH-MIDAS模型,发现该模型对于全球黄金期货市场月度波动率有显著的正向预测影响,在危机时期黄金期货市场波动有所增强;Wei等[3]利用脊回归模型研究CBOE黄金波动率指数对我国黄金期货波动率的预测作用,发现该模型减少了各种波动率预测因子的过度拟合和多重共线性问题;惠晓峰等[4]通过EGARCH和VAR-BEKK-GARCH模型研究2013年启动的夜盘交易模式对黄金期货价格的影响,发现该模式明显增加了市场交易积极性,降低了黄金期货长期波动率。

但是,这些研究主要关注于理性因素对于黄金期货的影响, 忽视了金融市场往往会受到投资者的情绪、偏好等因素影响这一实际情况, 使得传统的一些研究无法完全解释黄金期货市场的波动现象。 近些年来,越来越多的学者将关注力放在研究个人投资情绪上, 将这种非理性因素与市场变化联系起来, 例如Guiso等[5]提出投资者们在面对冲击时会受到个人情绪的影响, 从而改变他们在金融和非金融领域的冒险意愿。 但这些研究把风险厌恶情绪看作是恒定不变的, 与金融市场事实不符。 吴鑫育等[6]基于上证50期权的实证研究表明如果不考虑投资者时变的风险厌恶则会丢失相关资产变动的信息, 使得最终结果偏离实际;陈峥等[7]采用鞅方法将风险厌恶系数视作时变的, 得到了最优的投资策略。

本文利用最近提出的一种新的时变风险厌恶指标(RA)来研究黄金期货市场波动,即Bekaert等[8]提出的风险厌恶的新测度方法,该方法是由可观察到的高频金融信息构建的。这一度量方法依赖于六种金融工具,即期限利差、信用利差、非趋势股息收益率、已实现股权回报方差、风险中性股权回报方差以及已实现公司债券收益方差。Çepni等[9]将其应用于债券超额收益的预测,该研究发现RA包含了对未来期间利率变化的预测信息,可以用来帮助相关政策制定的改进;Riza等[10]在RA的基础上对套利交易的收益预测能力进行研究,得出套利交易收益的下跌与风险厌恶的提高显著相关的结论;Dai和Chang[11]利用RA来预测股票的已实现波动率,发现该指标的加入既可以得到良好的样本内拟合效果也可以获得精确的样本外预测效果。

综上可以看出,少有文献将时变风险厌恶指标引入黄金期货波动分析中。在仅有的一篇相关文献中Riza等[12]采用的是简单的HAR-RV模型,该模型建立在包含较少信息的同频数据基础上,势必会造成数据信息的缺失。考虑到本文使用的是黄金期货日度数据和RA月度数据,想要研究RA与波动率之间的关系,则需要考虑到两者之间的不同频率。鉴于此,为了保证信息的有效性和完整性,本文借鉴Engle等[13]提出的GARCH-MIDAS模型,将RA作为外生变量引入该模型框架中,研究RA对黄金期货波动率的影响及预测作用。该模型通过混频抽样技术将条件方差分解为长期与短期两个成分,能够克服不同频率的数据导致的复杂性,一经提出就在股票、汇率及原油等多个市场得到了广泛应用[14-17]。

二、 模 型

1. GARCH-MIDAS模型

GARCH-MIDAS模型对资产收益率建模,将资产收益率的条件方差分解为高频短期波动和低频长期波动两个部分,具体为

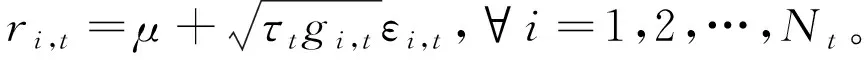
(1)

式中:ri,t为第t个月中的第i天的对数收益率;μ是ri,t的无条件均值,即E(ri-1,t)=μ;εi,t|Φi-1,t～N(0,1),即εi,t在Φi-1,t的条件下服从标准正态分布,其中Φi-1,t是第t个月中第i-1天的信息集合;gi,t为短期高频波动成分,服从GARCH(1,1)过程,具体形式为

(2)

式中:α、β是需要估计的参数,分别表示ARCH、GARCH参数,α>0,β>0且α+β<1,这样可以确保短期成分的非负性以及平稳性。

τt为低频长期波动成分,受到已实现波动率(RV)的影响,表达式如下:

式中:m为常数;θ1反映RV对长期成分τt的影响,θ1若是正数说明两者之间存在正相关关系,反之则存在负相关关系;RVt是资产的月度RV基于日度收益率的平方加总得到;Nt是第t月中交易日数;K为MIDAS回归的最大滞后阶数;φk(w1,w2)为加权系数。本文选择使用Beta权重函数,其形式为

(5)

为了保证滞后项权重呈现衰减形式(滞后期越小,对当前影响越大)和模型计算的简便,令ω1=ω2=1。由此得到简化后的Beta权重函数的具体形式如下:

(6)

对模型取对数形式,得到最终的GARCH-MIDAS模型

(7)

2.GARCH-MIDAS-RA模型

本文在单因子GARCH-MIDAS模型基础上引入外生变量,构造出新的多因子的GARCH-MIDAS-RA模型

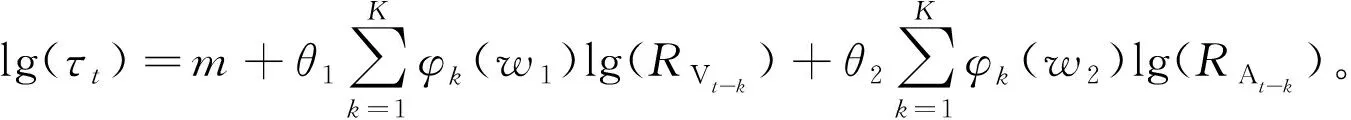
(8)

式中:RAt-k为本文引入的外生低频变量时变风险厌恶指标,θ1反映RA对长期成分τt的影响,θ2若为正说明两者之间存在正向的影响关系;θ2若为负则存在负向影响。

3.极大似然估计

上述模型中参数可以通过极大似然方法估计得到。该模型的对数似然函数为

(9)

式中:T表示交易数据中总的月份个数;Θ=(μ,m,θ1,θ2,ω1,ω2,γ,α,β)′是模型中待估参数组成的向量。进一步,模型参数的极大似然估计值可以通过最大化对数似然函数得到

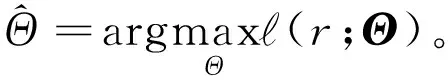
(10)

4.模型预测的检验函数

本文通过采用MAE(平均绝对误差)、MSE(均方误差)、QLIKE(拟似然)3种损失函数来判断模型预测能力。计算公式如下:

进一步地,本文利用模型置信集(model confidence set,MCS)对不同的模型进行比较。

MCS检验过程:对文中构建的模型进行一系列的显著性检验,剔除表现较差的模型,得出幸存模型。该检验中用到的统计量包括范围统计量(range statistic)和半二次方统计量(semi-quadratic statistic),定义如下:

式中:dij是模型i和模型j的平均相对损失函数值;M代表模型的集合,i,j∈M。

三、 数 据

1.数据的选取和说明

由于不同黄金期货合约之间的差异较小,通过交易数量的对比,并且考虑到T+D的交割时间没有限制、合约存在高流动特性,本文选择的黄金期货合约为上海黄金交易所的AU(T+D),所用价格数据为其每日收盘价。样本选择的时间为2010年1月1日至2021年6月30日,共2 792个数据。数据来源于WIND资讯数据库。

时变风险厌恶指标样本的选取为2010年1月至2021年6月共138个月度数据。从https:∥www.nancyxu.net/RA-aversion-index下载得到。

本文使用黄金期货的对数收益率,即当日收盘价的对数减去上一交易日的收盘价的对数计算得到

rt=lnpt-lnpt-1。

(17)

从图1中可以看出,黄金期货收益率第一个大的波动处在2011年附近。2011年欧债危机爆发,意大利、希腊等欧洲国家的股票市场、债券市场暴跌,随后美国首次丧失3A主权信用评级,这一系列的事件引起了世界各地的担忧与恐惧,全球股市遭遇“黑色星期一”。投资者增加了对于黄金期货的需求(人们试图通过黄金的避险特征来减少损失)。第二个大的波动在2020年。由于新型冠状病毒肺炎疫情的突然爆发以及地缘政治的增强,黄金期货的需求量有了较高上涨,2021年随着疫情逐渐减轻,人们预测市场将出现较快的经济复苏,因此黄金期货开始高位回落。时变风险厌恶指数在这两段时间内也有比较大的波动(图2),并在2012年、2020年达到了阶段性的最高点。

图1 黄金期货对数收益率时间序列图

图2 时变风险厌恶指数时间序列图

2. 描述性统计

对黄金期货的对数收益率ri,t及RA进行描述性统计分析,结果如表1。可以看出,ri,t的偏度为-0.692 4,小于0,即整体数据分布不对称,呈现左偏,峰度为11.736 6,大于3,即明显偏离正态分布,该数据具有“尖峰厚尾”的特征。RA的偏度为3.061 0,呈现右偏状态,峰度为14.911 1也远大于3,同样偏离正态分布,具有“尖峰厚尾”特征。与ri,t相比,RA拥有更大的均值和标准差,即RA的波动性较大。对于LB相关检验(Ljung-Box)自相关检验,我们检验了10阶和20阶的序列相关性,可以看出ri,t和RA均在1%置信水平显著,即序列存在很强的自相关性。Jarque-Bera检验下各变量序列在1%水平也是显著的,且该统计量的数值很大,这表明序列具有长记忆性。

表1 描述性统计量

四、 实证分析

1. 模型估计结果

在本节中,我们将研究GARCH-MIDAS波动率模型的参数估计。设定模型中外生变量的滞后期参数为K=12,即RA对于黄金期货市场波动影响的滞后时间为12个月。参数估计结果见表2。其中α、β为GARCH过程的参数;θ1、θ2反映RV、RA对黄金期货波动率长期成分的影响;ω1、ω2是对应变量的Beta权重函数最佳估计数。

表2 模型参数估计结果

从表2可以看出:GARCH-MIDAS和GARCH-MIDAS-RA模型除了μ的参数估计结果以外,其他参数的系数均是显著的。GARCH部分的参数显著说明黄金期货的短期波动具有较为强劲的聚集效应;长期均值μ不显著,α+β小于1但趋于1,表明黄金期货的价格波动具有高的持续性,模型的短期成分拟合程度好,并且这种效应随时间的加长而慢慢减弱。所以本文构建的模型是稳定的。θ1值为正且显著,说明本期黄金期货RV增加时,既会影响短期内的波动,下期波动率的长期成分也会明显增加。θ2值为正说明RA与黄金市场的波动率有正向的相关关系,这是因为当投资者认为市场状况存在较大风险时,他们会更加倾向于抛弃高风险的资产转而购买拥有避险特征的黄金。ω1=1.163 7、ω2=261.723 8均大于1,这表明RV与RA滞后项的Beta权重系数在滞后时间增加情况下显示出逐步下降趋势。对数似然值越大,信息准则AIC结果越小说明模型的拟合优度越好。从表2的结果可以明显看出相对于基准的GARCH模型而言,考虑MIDAS的模型有很大程度的优化。更进一步,GARCH-MIDAS-RA模型样本内的拟合优度优于GARCH-MIDAS模型,这说明加入了时变风险厌恶后的模型有更大的优化作用。

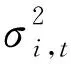
(a) GARCH-MIDAS模型的长期成分(b) GARCH-MIDAS-RA模型的长期成分

2. 样本外预测分析

样本外预测分析用来检验加入RA是否提高了模型的预测精度。损失函数值越小表明预测值与实际值之间的差别越小,即模型的预测精度越好。本文将样本数据划分为“样本内拟合样本”和“样本外预测样本”两部分,其中,前2 000个数据是观测样本,后791个数据为预测样本。采用滚动时间窗方法进行样本外估计,得到791个预测值。利用公式(11)、(12)和(13)计算出MAE、MSE和QLIKE,结果如表3所示。

表3 黄金期货样本外预测结果

从损失函数值可以看出:相对于基准模型(GARCH模型、GARCH-MIDAS模型),GARCH-MIDAS-RA模型在绝大多数情况下都具有更优的预测能力,这说明加入了RA指数确实能够提高模型的预测精度。

3. MCS检验

MCS检验的置信水平取0.1,即MCS检验中,如果模型的p值小于 0.1,表示该模型的预测能力较差,模型效果不佳;如果p值大于0.1,说明该模型的样本外的预测能力更优,p值越大,预测精度越高。MCS检验结果如表4。

表4 MCS检验结果

线表明该模型在对应的损失函数下拥有最优的预测精度。

从表4看出:GARCH模型在所有的损失函数下MCS的p值均为0,这表明该模型预测黄金波动率的效果不佳,是三个模型中预测精度最差的模型。考虑了混频数据的GARCH-MIDAS模型的预测能力显著优于仅考虑同频数据的GARCH模型,这表明时变风险厌恶对于黄金市场波动影响并非是同步的,采用同频的数据会丢失这种非同步的传递关系。进一步地观察GARCH-MIDAS-RA模型,MAE、QLIKE均取得了最高的P值(p=1),即通过了MCS检验,MSE的p值为0.996 5接近于1,这表明该模型对于预测黄金期货市场波动有最优效果,时变风险厌恶确实能够有效提高黄金期货市场波动的预测精度。

4. 稳健性检验

本节主要是检验模型的样本外预测能力是否具有稳健性特征。通过改变滚动时间窗口来比较构建的模型预测能力差异,以验证结论的稳健性。本文选择的样本外预测长度分别为50 d、100 d、500 d。表5是不同长度下的MCS检验结果。

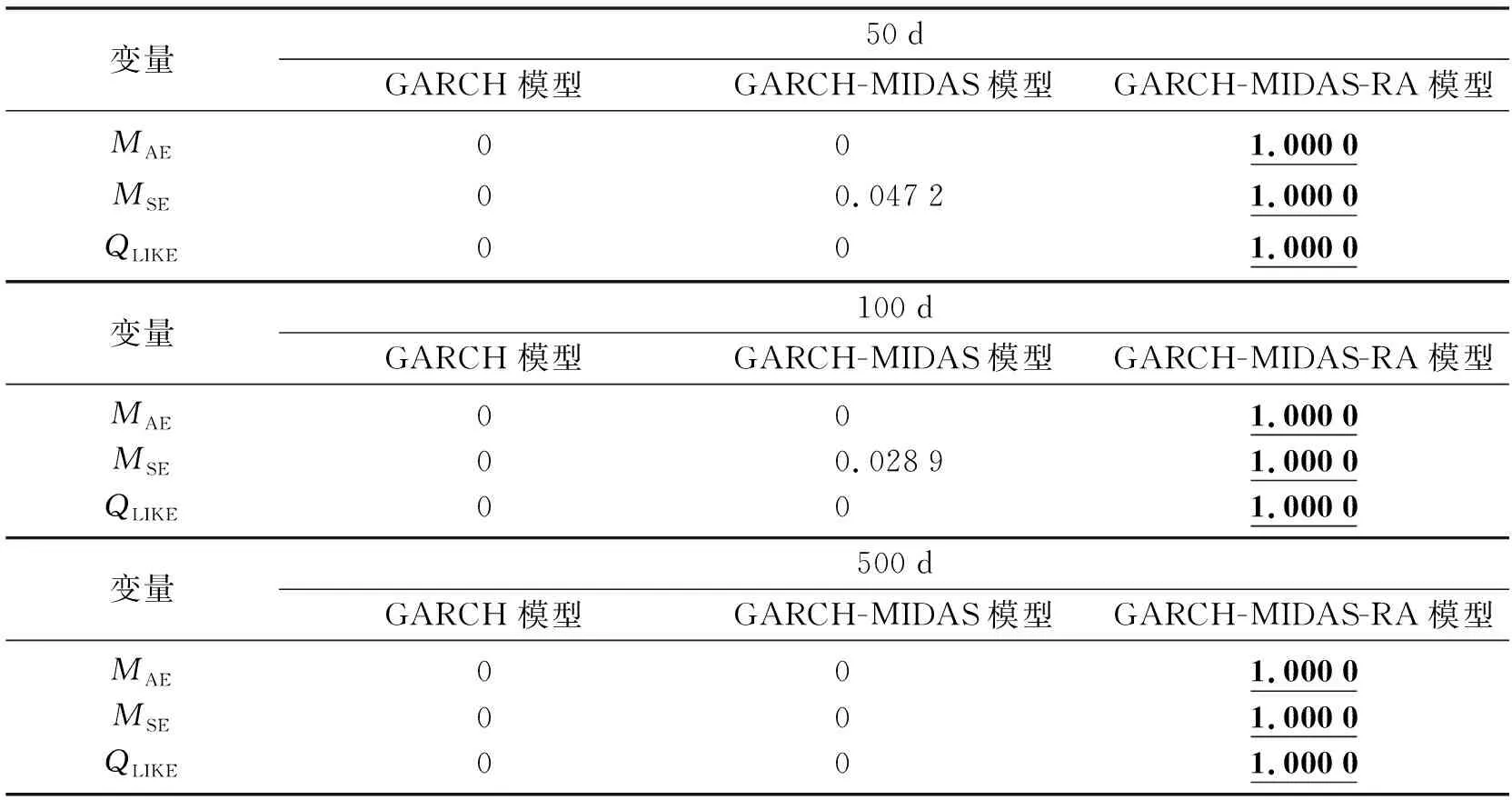
表5 MCS 检验结果:不同的预测窗口

从表5中可以看出不同的预测窗口下得出的结论与上文是一致的,GARCH-MIDAS-RA模型在每一个损失函数下都通过了MCS检验且获得最大的p值,显著说明了该模型对于预测中国黄金期货市场波动率具有极大的优势且该预测能力具有稳健性。

五、 结 论

与一般的金融资产不同,黄金作为一种拥有多重属性的实物资产,一直被人们看作是减缓经济和政治冲击的有效工具。而对波动率进行建模和预测一直以来都是金融领域的热点话题,因此对黄金期货波动的变动趋势进行估计和精确预测对于投资者进行投资组合和风险管理极为重要。在这样的背景下,本文采用了Bekaert等提出的RA指数来研究其对黄金期货波动率的影响。由于文中同时使用了上海黄金交易所的黄金期货日度数据和月度RA数据,防止数据信息的丢失,本文选择使用GARCH-MIDAS模型,将RA引入模型中来进一步研究其对黄金期货市场波动率的影响和预测作用。

实证研究结果表明:RA指数对黄金期货市场波动率产生了积极显著的影响;本期黄金期货RA增加时,既会影响短期内的波动,也会影响下期波动率的长期成分。预测精度检验函数结果表明:与GARCH模型相比,GARCH-MIDAS模型能够提供更准确的预测结果;更进一步,将RA纳入GARCH-MIDAS模型能够显著改进黄金期货市场波动的样本外预测能力,即本文构建的GARCH-MIDAS-RA模型具有最优的表现。此外,本文通过稳健性检验得到了与实证结果一样的结论。