沥青混凝土心墙风化料坝施工及蓄水过程模拟
2022-12-01孙立国江守燕杜成斌黄文仓黎亚生曹庆明
孙立国 江守燕 杜成斌 黄文仓 黎亚生 曹庆明
(1. 河海大学 力学与材料学院, 南京 211100; 2. 云南省水利水电勘测设计研究院, 昆明 650021)
土(堆)石坝因具有就地取材、工程造价低、便于施工等优点[1],已经成为世界大坝工程建设中应用最为广泛和发展最快的一种坝型.沥青混凝土心墙坝作为一种新兴的坝体结构,由于具有良好的抗渗性、抗震性、低成本和适应变形的能力,已成为一种非常有竞争力的坝型[2],被国际大坝委员会认为是未来高坝的适宜坝型之一[3].此外,经济分析研究结果表明,沥青混凝土心墙坝的设计施工不受气候条件的影响,可以缩短施工时间,获得更大的经济效益[4].虽然沥青混凝土心墙坝仍处于发展阶段,但至今为止,我国已建成的沥青混凝土心墙坝运行状态良好,产生了较大的社会效益与经济效益.随着沥青混凝土心墙坝的广泛应用,在大坝设计施工过程中,坝体应力和变形分析已成为一个重要环节[4-7].
利用有限元法对沥青混凝土心墙坝进行计算分析时,常用的材料本构模型有邓肯-张E-ν、E-B模型、南水模型、清华K-G模型等[8].邓肯-张模型是典型的非线性弹性模型,该模型的弹性模量是应力状态的函数,可以描述粗粒料应力-应变关系的非线性和压硬性.虽然邓肯-张模型存在一些局限性,但因其能较好地模拟土石料的力学性质,并具有参数少、形式简洁的特点,除应用于岩土体的应力、应变研究外,也可应用于沥青混凝土等材料的应力、应变性质的研究[9].使用有限元法对土石坝进行数值分析时,通常会对模型进行一定的简化,数值结果的合理性较难验证[1,8,10-13],实际的工程条件相当复杂,如何进一步验证有限元计算结果的准确性至关重要.
论文利用开发的邓肯-张本构模型子程序[14],根据现场施工资料拟定大坝施工及蓄水过程模拟方案,重点对比分析了施工期沥青混凝土心墙风化料坝的有限元结果与监测数据,验证了大坝施工及蓄水模拟的有限元模型的正确性与合理性,其相应蓄水期的有限元预测结果也为大坝蓄水后的安全性与稳定性提供了理论支持.
1 工程概况
轿子山水库地处昆明市东川区红土地镇境内,位于金沙江流域小江左岸一级支流小清河中游,属金沙江水系二级支流.水库坝址以上控制流域面积145 km2,多年平均径流量17 917万m3.水库大坝采用沥青混凝土心墙风化料坝,其典型剖面如图1所示,坝顶高程2 204 m,最大坝高99 m,坝顶轴线长320 m,坝顶宽10 m.大坝上游坝坡在高程2 179、2 153 m处分别设有一台马道,将坝坡分为三级,各级坡比由上到下分别为1∶2.25、1∶2.25、1∶2.5.下游坝坡共设三级马道,高程分别为2 179、2 154、2 129 m,高程2 179 m以上坝坡为1∶2.1,2 154至2 129 m高程间坝坡为1∶2,其下部由于采用弱风化砂岩填筑而将坝坡设计为1∶1.8.沥青混凝土心墙设置于大坝坝轴线上游2 m处,采用碾压式施工工艺,心墙采用垂直分段等厚设计,共分4段,自上而下分别为0.5、0.7、0.9、1.1 m,心墙底部3 m高范围内两侧按1∶0.2边坡扩大后与宽8 m的混凝土基座相连,基座厚1.5 m,心墙上下游各设置水平宽度3 m的过渡层.水库正常蓄水位2 201.50 m,死库容315万m3,兴利库容1635万m3,总库容2 033万m3,水库调节性能为不完全年调节.

图1 大坝典型剖面及心墙示意图(单位:m)
坝址区内地层岩性主要是第四系人工堆积、崩坡积、冲洪积、残坡积层,下伏长石石英砂岩和粉砂质泥岩,其中弱风化长石石英砂岩属中硬岩,粉砂质泥岩属较软岩.大坝基础部分的表层为6.0~26.0 m厚的强风化基岩,更深处为弱风化基岩.
2 监测布置
为评价轿子山水库大坝的施工质量,掌握大坝在施工期和运行期的工作状态,预测工程性态的发展、评估其安全可靠程度.根据现行规范[15],并结合轿子山水库大坝的结构特点,对轿子山水库大坝的安全监测进行了设计以及施工期的安全监测.大坝主要布置了3个监测断面,分别为坝横0+60.0 m、0+140.0 m和0+220.0 m剖面.为了解大坝沥青混凝土心墙及心墙混凝土基座应力应变的分布情况,在沥青混凝土心墙及心墙混凝土基座布置了单向应变计,呈对称布置,如图2所示.为掌握坝基在坝体荷载作用下的变形情况,在沥青混凝土心墙后坝体与坝基结合处自上而下布置了沉降计,各断面沉降计分布如图3所示.
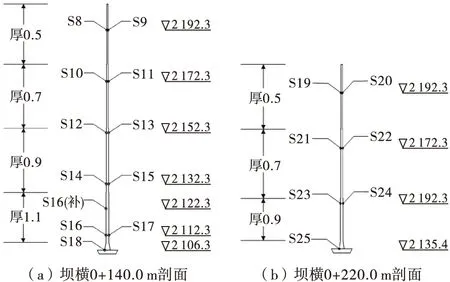
图2 心墙应变计分布图(单位:m)

图3 各断面沉降计分布图(单位:m)
3 材料本构模型
针对不同类型的材料,采用两种本构模型:线弹性模型和邓肯-张E-ν非线性弹性模型(邓肯-张E-ν模型).基岩、混凝土基座和帷幕采用线弹性模型,其材料参数见表1.

表1 线弹性模型材料参数
坝壳砂岩泥岩强弱风化料、弱风化砂岩堆石料、沥青混凝土及过渡料在计算时采用邓肯-张E-ν模型.
加载时,邓肯-张E-ν模型的切线模量为

(1)
式中:s为应力水平,其表达式为

(2)
为考虑土石料材料强度的非线性,内摩擦角为
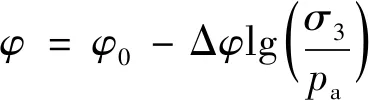
(3)
若单元处于卸荷或再加荷状态,改用回弹模量表示如下:
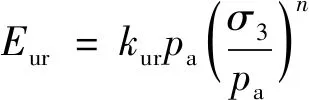
(4)
切线泊松比为

(5)
式中:
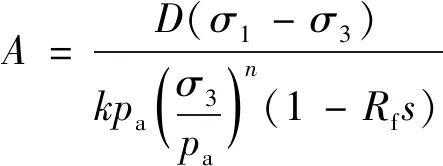
(6)
式中:pa为大气压;弹性模量中的无因次系数k、n,破坏比Rf;强度指标c、φ、φ0、Δφ;侧向变形系数G、F、D可由土石料的静三轴试验得到.邓肯-张材料参数见表2,其中ρ为密度,kur为卸荷模量.
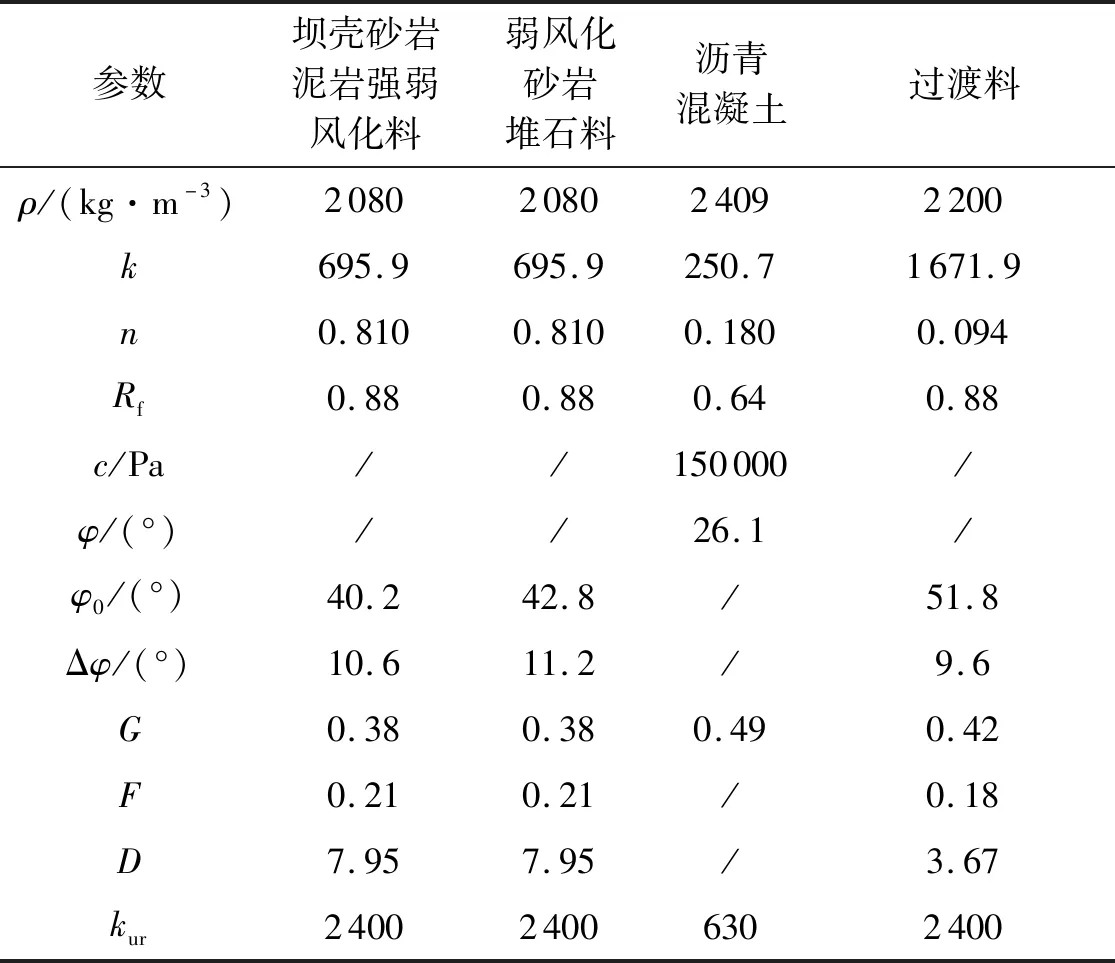
表2 静力计算邓肯-张E-v模型参数
4 施工及蓄水过程模拟
4.1 三维有限元模型
根据该沥青混凝土心墙坝的平面布置图和剖面图建立三维有限元模型,三维有限元网格如图4所示.以顺河流方向为x轴方向,指向下游为正;铅直方向为z轴方向,铅直向上为正;以坝轴线方向为y轴方向,指向左岸为正.有限元网格以八节点六面体单元为主,在边界处布置了少量的楔形体单元来适应坝体形状变化及协调材料分区.坝体和地基系统的节点总数为156 158个,单元总数为148 171个,其中坝体包含36 905个节点和33 213个单元.基岩范围沿上、下游分别延伸约2倍最大坝高,向基础深部延伸约2倍最大坝高.为方便网格剖分同时减少畸形网格单元,网格剖分时坝坡近似采用台阶状拟合.

图4 三维有限元网格
在计算过程中考虑坝体自重、静水压力及浮力,其中静水压力直接施加在沥青混凝土心墙上游面,坝体的应力-变形计算主要有以下3种荷载组合工况.工况1(竣工期):坝体自重+施工期水位(上游水位2 137 m);工况2:坝体自重+死水位(上游水位2 165 m);工况3(满蓄期):坝体自重+正常蓄水位(上游水位2 201.50 m).
4.2 大坝施工及蓄水过程分级模拟方式
大坝的填筑过程和蓄水过程采用分级加载的方式进行模拟.根据现场施工资料显示,大坝在施工期的上游水位随着大坝填筑高程增高而增高,最后稳定在2 137 m高程左右.为了使施工过程模拟更符合实际情况,大坝在施工过程模拟中采用边施工边蓄水的方案,当上游水位达到2 137 m高程后不再蓄水,直至大坝填筑至坝顶后(高程为2 204 m),将再次进行蓄水.综合考虑大坝实际施工过程及网格质量,施工及蓄水过程分18级进行,具体的大坝施工及蓄水过程模拟如图5和表3所示.

图5 大坝施工及蓄水过程分级模拟方式示意图(单位:m)

表3 大坝施工及蓄水过程分级模拟方式
4.3 心墙垂直应变对比分析
选取坝横0+140.0 m剖面与坝横0+220.0 m剖面处的心墙垂直应变进行对比.由于大坝施工现场所选用的应变计为混凝土应变计,量程范围为±3 000×10-6.
参考茅坪溪[16]、冶勒[17]等类似工程的监测数据可知,该应变计由于量程限制而无法记录沥青混凝土心墙应变增长的完整过程,故选取完好的应变计量程内的实测数据与相应计算结果进行对比分析.分别选取S11、S15、S17、S24四个比较具有代表性的应变计实测数据进行对比,对比结果如图6所示.
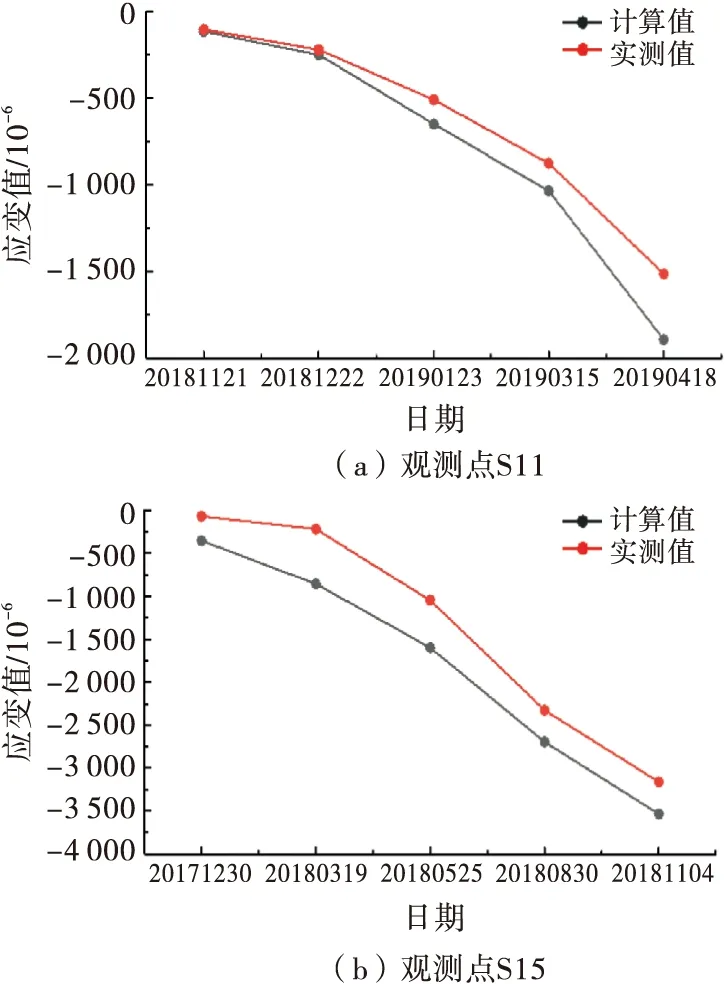
图6 应变计实测值与计算值对比
从图6中可以看出,4个应变计所在位置的垂直应变计算值和实测值过程线的趋势和数值相差不大,基本上保持一致.实测值与计算值间存在的误差可能是由应变计的安装方式、施工现场的不确定因素、计算的简化性等原因引起的,但两者间的误差都在可接受范围内.
总体而言,应变计的实测值与计算值是基本吻合的,从而验证了施工模拟计算结果的合理性与正确性,同时也说明本次数值模拟结果能较好地反映出沥青混凝土心墙垂直应变在施工期的变化规律.
4.4 坝基沉降值对比分析
考虑到部分沉降计已发生损坏等原因,并结合沉降计分布情况,分别从坝横0+60.0 m、0+140.0 m、0+220.0 m剖面中各选取一个具有代表性的沉降计测点进行对比分析,分别为M3、M8、M10沉降计测点,具体对比结果如图7所示.
由图7可知,这3个应变计的实测值与计算值在变化趋势上是一致的,但在数值上存在较大误差,尤其是M3、M8两个应变计的实测值与计算值相差较大.产生这些差别的原因可能有以下两点:首先是坝基沉降值的数值较小(仅为几毫米),这会导致现场测量误差对结果产生较为明显的影响;其次是实际工程中的坝基的地质条件较为复杂,部分区域可能存在软弱层与破碎带,而有限元计算中难以完整地考虑这些因素,从而导致了现场实测值与计算值之间的差距.总体而言,坝基沉降值的对比结果在一致性上虽不及心墙垂直应变的对比结果,但计算结果在变化趋势和数量级上仍与实测结果较为一致,说明施工模拟的计算结果具有一定的合理性.

图7 沉降量实测值与计算值对比
4.5 心墙和坝体的应力变形计算结果分析
图8给出了满蓄期沥青混凝土心墙变形及应力分布,图9给出了满蓄期最大横剖面(坝横0+140.0 m剖面)的变形及应力分布,表4列出了由三维有限元静力计算得到的沥青混凝土心墙和坝体的变形及应力极值.

图8 满蓄期沥青混凝土心墙变形及应力分布
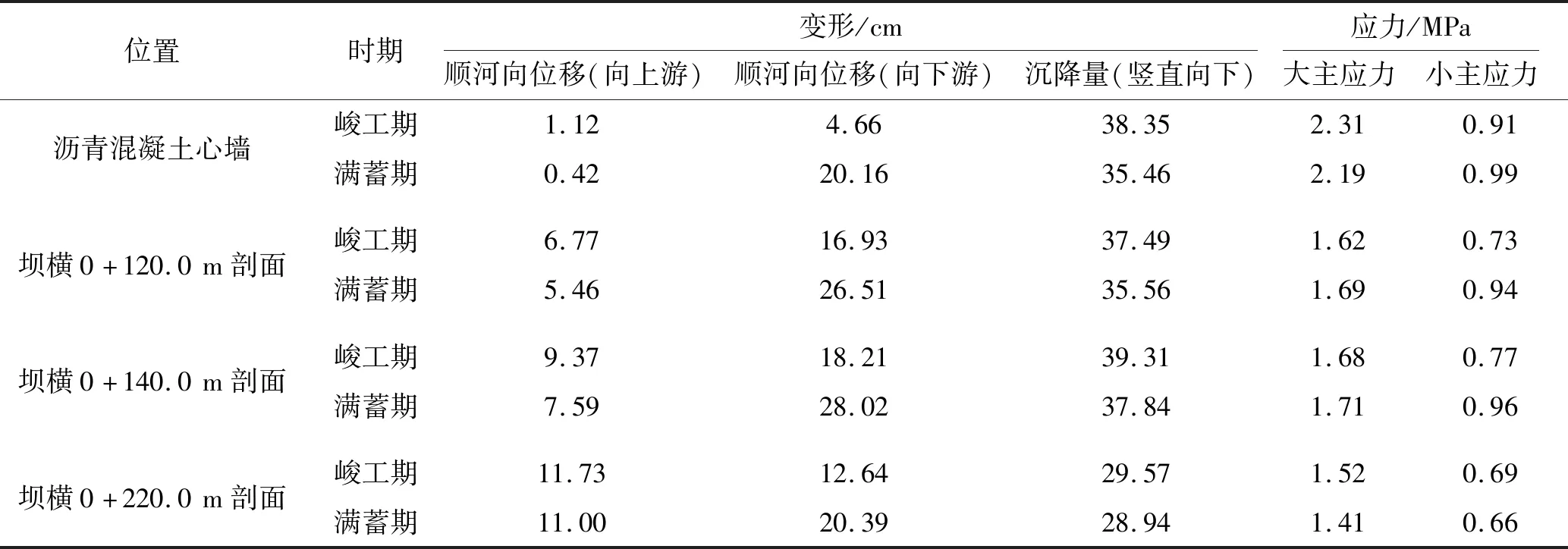
表4 沥青混凝土心墙和坝体的变形及应力极值
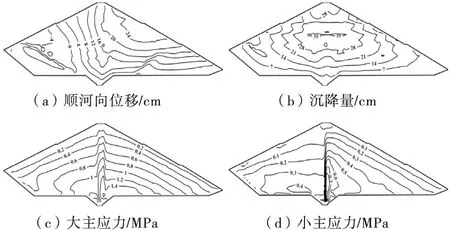
图9 满蓄期坝横0+140.0 m剖面变形及应力分布
由表4的计算结果可以看出,竣工期心墙向下游的顺河向最大位移为4.66 cm,蓄水后心墙受到水压力作用,满蓄期向下游的心墙顺河向位移明显增大,最大值为20.16 cm,发生在约2/3坝高处.各工况的心墙最大沉降量均发生在约2/3坝高处,竣工期心墙沉降量达最大值,为38.35 cm,占最大坝高(99 m)的比例为0.39%.沥青混凝土心墙的大小主应力从坝顶向下逐渐增大,最大值均发生在心墙底部.大坝在蓄水后,由于受到静水压力与浮力的作用,心墙大主应力有所减小,小主应力有所增大.大主应力在竣工期达最大值,为2.31 MPa.小主应力校核洪水位工况下达最大值,最大值为0.99 MPa.心墙横河向基本未出现拉应力.
从坝体的顺河向位移分布图可以看出,坝体的顺河向位移整体偏向下游,顺河向位移最大值发生在约2/3坝高的下游坝坡处,蓄水后坝体向下游的顺河向位移较竣工期明显增大,其中竣工期顺河向位移最大值为18.21 cm,满蓄期顺河向位移最大值为28.02 cm.坝体沉降量最大值发生在约2/3坝高处,竣工期坝体沉降量达最大,为39.31 cm,占最大坝高(99 m)的比例为0.40%.由于蓄水后坝体受到浮力作用,故坝体沉降量在蓄水后有所减小.坝体大小主应力的分布自坝顶向下逐渐增大,且最大值均发生在底部的混凝土基座附近.由于过渡料和心墙的模量差异,大主应力等值线在心墙和过渡料之间出现了拱效应,这和通常土石坝的应力计算规律是一致的.竣工期大小主应力最大值分别为1.68和0.77 MPa,满蓄期大小主应力最大值分别为1.71和0.96 MPa.
5 结 论
本文以轿子山水库沥青混凝土心墙风化料坝为研究对象,拟定相应的施工及蓄水过程模拟方案,对比分析了施工期沥青混凝土心墙风化料坝的有限元计算结果与对应位置现场监测结果.在此基础上,对大坝满蓄期的应力-变形进行了预测计算,得到以下几点结论:
1)施工期心墙垂直应变和坝基沉降计算值和实测值的变化趋势与数值基本上保持一致,验证了施工模拟的有限元模型的合理性与正确性.
2)竣工期心墙向下游的顺河向最大位移为4.66 cm,蓄水后心墙受到水压力作用,满蓄期向下游的心墙顺河向位移明显增大,最大值为20.16 cm,发生在约2/3坝高处.心墙最大沉降量发生在约2/3坝高处,竣工期心墙沉降量达最大值,最大值为38.35 cm,占最大坝高(99 m)的0.39%.
3)沥青混凝土心墙的大小主应力从坝顶向下逐渐增大,最大值均发生在心墙底部.大坝蓄水后由于受到静水压力与浮力的作用,心墙大主应力有所减小,小主应力有所增大.
4)坝体的顺河向位移整体偏向下游,最大值发生在约2/3坝高的下游坝坡处,其中竣工期顺河向位移最大值为18.21 cm,满蓄期顺河向位移最大值为28.02 cm.坝体沉降量最大值发生在约2/3坝高处,竣工期坝体沉降量达最大,最大值为39.31 cm,占最大坝高(99 m)的0.40%.
5)坝体大小主应力的分布自坝顶向下逐渐增大,且最大值均发生在底部的混凝土基座附近;由于过渡料和心墙的模量差异,大主应力等值线在心墙和过渡料之间出现了拱效应,这和通常土石坝的应力计算规律是一致的.
施工及蓄水过程模拟计算得到的大坝应力-变形符合沥青混凝土心墙坝的一般分布规律,且量值基本合理.整体而言,在施工及蓄水模拟的有限元模型的正确性得到验证的前提下,通过该模型计算得到的满蓄期大坝变形及应力性态良好,为大坝蓄水后的安全性与稳定性提供理论支持,大坝蓄水后的安全运行是有保障的.
