基于运动力学分析的六轴机械臂牵引控制设计
2022-12-01杨宽金建辉
杨宽,金建辉
(650504 云南省 昆明市 昆明理工大学 信息工程与自动化学院)
0 引言
随着网络和智能化技术的发展,制造业也在向智能化、自动化方向发展,作为高端制造业的主要手段,机器人产业迎来了新的发展机遇。机械臂作为高端且实用的机器人,潜力巨大、发展最为迅速[1]。机械臂的发展弥补了传统机器人工作能力差、执行任务单一、适应性弱等缺点,为利用机器人进行生产制造提供了机会。
通过控制接触力在机械臂执行末端的位置约束机械臂的活动自由度,对接触力的控制精度要求较高。例如,利用机械臂擦拭玻璃时,不仅要准确控制机械臂的切向接触力以实现对玻璃接触面切向轨迹的有效控制,还要实现对法向接触力的大小进行有效控制以避免损坏玻璃。如果切向接触力的控制效果不好,机械臂就无法与玻璃表面接触,擦拭玻璃的任务就会失败;或者法向接触力过大,就会造成玻璃的损坏[2]。另外,在多轴机械臂所执行的任务中,对接触力的控制要求更为严格。在任务执行的受限运动中,通过接触力控制轨迹以实现机械臂的位置变化时,会造成力的变化,这就导致了机械臂位置控制所要求的高刚性与接触力控制所要求的高柔性之间的矛盾[3]。
本文以六轴机械臂的机械结构及其精确建模为基础,建立运动学模型,通过联合静态力学以及正向和反向运动力学分析,采用关节空间和笛卡尔空间的轨迹规划方法,精确控制关节的运动轨迹,最后通过仿真平台软件进行了平面轨迹定位实验。
1 六轴联动机械臂的机械结构
六轴联动机械臂利用安装的电机驱动轴承和连杆,实现对动作臂的控制,最终实现运动。因此,由多级电机驱动的自由臂实现了多自由度的关节运动,可以使六轴联动机械臂在复杂的环境中进行操作[4]。六轴机械臂的关节结构分析如图1 所示。
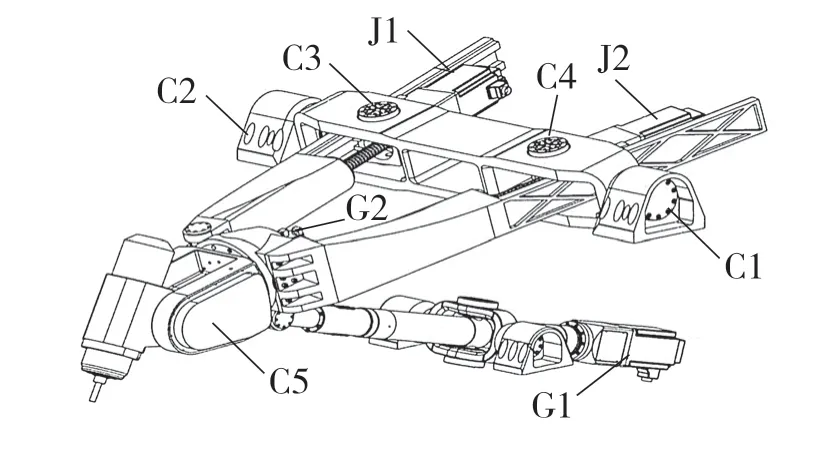
图1 六轴联动机械臂的机械结构Fig.1 Mechanical structure of six-axis linkage manipulator
图1 中,G1 和G2 为2 个直流电动机,J1 和J2是2个行星式减速器,C1、C2和C5是等径伞齿轮,C3 和C4 是双连杆连接机构。
2 六轴联动机械臂的运动力学分析
2.1 静态力学分析
如图2 所示,定义Lei表示六轴联动机械臂直线模型中连杆从Q0到Q1的直线距离;Li是运动模型中连杆从Q0到Q1的运动长度;g是重力加速度[5]。在连杆1 和连杆2 的坐标系中,Fi(i=1,2)表示连杆末端效应器处的拉力;Fxi是拉力的水平分量;Fzi是拉力Fi的垂直分量;Xiend、Ziend是末端效应器的位置坐标,由此可得连杆处于静态时末端效应器位置处的运动公式[6]。

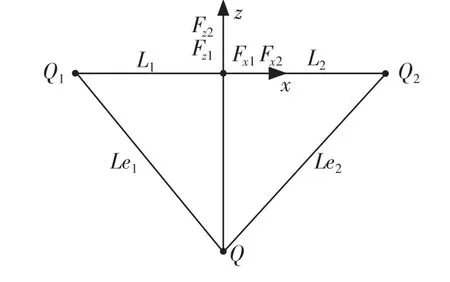
图2 静态力学分析图Fig.2 Static mechanics analysis diagram
假设点Q 在EXZ 坐标系中的坐标为(xstr,zstr),在e1x1z1或e2x2z2坐标系中的坐标为(xiend,ziend),可得Q 点在各坐标系中位置坐标的变换公式[7]。
对EXZ 坐标系中末端效应器进行静态力学分析。其中,Wi是连杆1 和连杆2 对末端效应器的拉力,Fi是力和反作用力。图3 中,Wxig 和Wzig是X 轴和Z 轴上连杆拉力的分力。在静态力学平衡下,可以得出EXZ 坐标系中的受力平衡公式。可以从Fxi、Fzi、Wxig 和Wzig 之间的线性关系得出eixizi和EXZ 之间的坐标变换[8]。
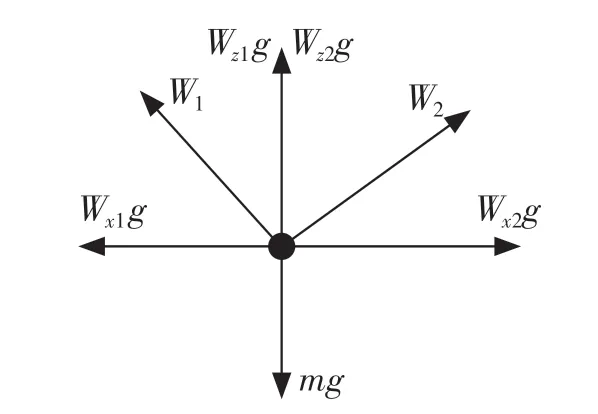
图3 末端效应器的静态力学分析Fig.3 Static mechanical analysis of end effectors
2.2 运动力学分析
2.2.1 运动力学反向分析
六轴联动机械臂的运动力学反向分析是求解未知数Fxi、Fzi、Li和EXZ 坐标系下的末端效应器的坐标(xstr,zstr)的一种有效方法。
首先在线性模型下求解连杆张力和连杆长度,然后将该结果作为运动模型下的初始值,采用数值迭代法求解运动公式。根据模型分析可得平面机械图,如图4 所示。
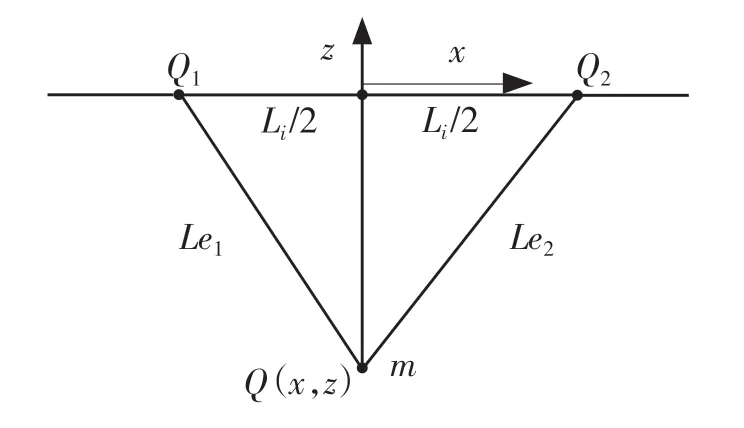
图4 线性模型机械图Fig.4 Linear model mechanical drawing
给出Q,Q1和Q2的坐标,根据图4 可以得到线性模型下连杆的长度Lei。假设Qi点的坐标为(Qxi,Qzi),末端效应器的坐标为(x,z),则
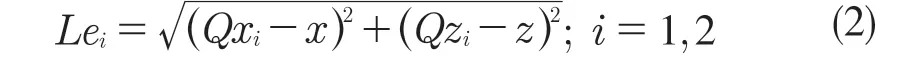
当连杆直线模型处于平衡时,对应的雅各布矩阵U 为
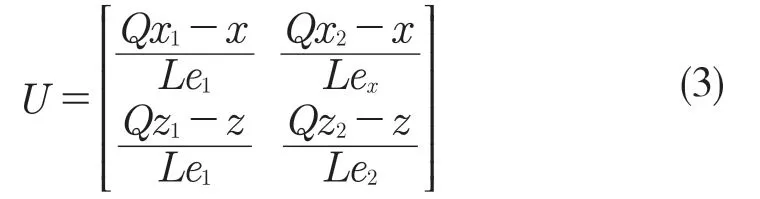
根据力学平衡公式,从图4 中可以得出线性模型下连杆拉力公式:

通过线性公式计算未知的张力矢量。根据式(3)、式(4)和连杆的静态力学分析,可得基于运动学的力学公式。

已知量为坐标系EXZ 中末端效应器Q 的位置坐 标(xstr,zstr),未知量为Fx1,Fz1,L1,Fx2,Fz2和L2。6 个未知量的初始值可由连杆线性模型确定。
式(6)中,X1end,X2end,Z1end和Z2end的值可根据xstr、zstr和式(3)得到。
2.2.2 运动力学正向分析
运动力学正向分析是运动力学反向分析的相反过程。式(5)中,L1和L2作为已知量,Fx1、Fz1、Fx2、Fz2、Xiend和Ziend为未知量。当使用数值方法求解非线性公式时,在线性模型下得到的拉力Wi、Xiend和Ziend也被作为初始值。首先,将已知量L1和L2视为线性模型下的连杆长度,利用几何方法得到EXZ 下末端执行器的坐标,如图5 所示。

图5 直线模型的几何关系图Fig.5 Geometric diagram of a linear model
3 实验分析
为了证明本文研究所提方案的有效性,在MATLAB 中利用MATLAB Robotics 工具箱进行了仿真实验。通过对比计算结果,验证了六轴联动机械臂运动模型建立和求解的正确性。设置机械臂的初始位置为(0,0),让机械臂沿2 cm×2 cm 的矩形路径和半径为2 cm 的圆形路径运动。通过人工控制定位进行比较和参考,得到最佳控制参数。
由图6 可知,通过修正机械臂定位和运动误差,定位精度呈现缩小趋势。与人工定位相比,机械臂的跟踪误差在中心点逐渐收敛,并趋于较小的误差。为了验证控制算法的精度控制误差范围,对迭代循环机械臂的运动轨迹进行了测试,如图7 所示。

图6 六轴机械臂的定位和分布比较Fig.6 Comparison of positioning and distribution of six-axis manipulator
图7 中,在多次迭代过程中,一段时间内的自由队形轨迹分布基本控制在0.2 mm 以内。由于控制算法的模糊效应是对精度的修正,所以脉冲运动与控制逻辑设计基本一致,满足精度的控制要求。
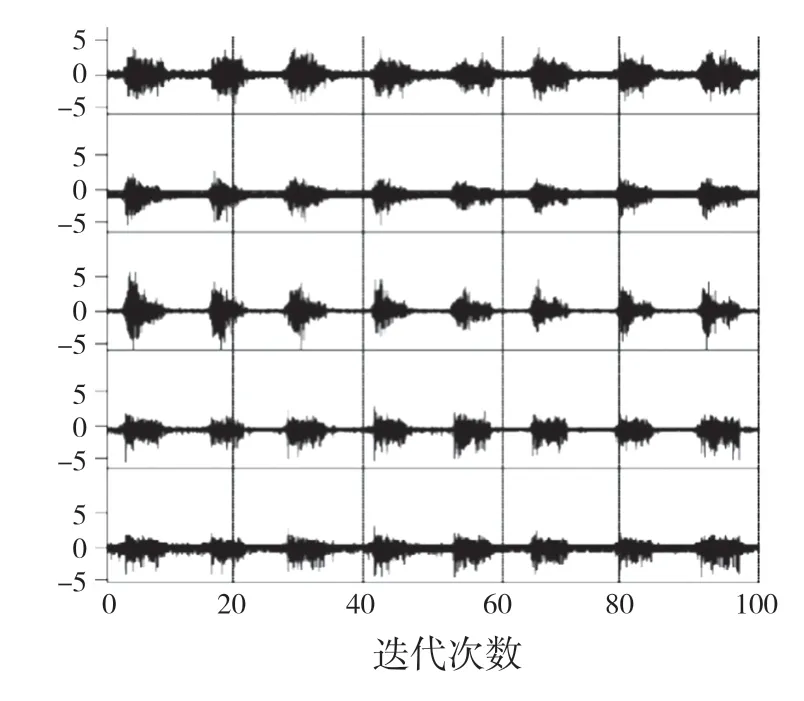
图7 六轴机械臂的运动轨迹的迭代测试Fig.7 Iterative testing of motion trajectory of six-axis manipulator
经过计算和求解,可以通过仿真得出连续执行情况下的末端效应器的精度模型,如图8 所示。
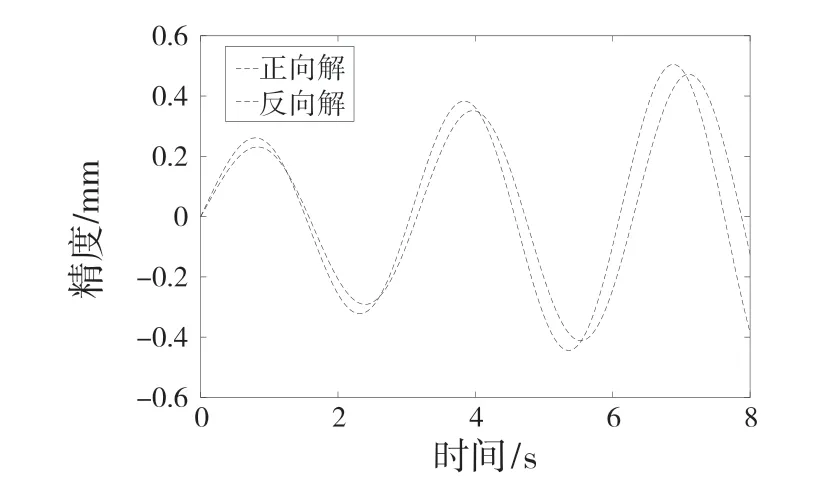
图8 连续执行运动力学分析精度模型Fig.8 Precision model of continuous execution kinematic mechanics analysis
由图8 可见,结果与模型的预期形状特征是一致的。在末端效应器的工作空间中选择一个子区间,在这个子区间内选择大量的不同位置的坐标进行模拟计算的反复测试,结果表明该算法可以使运动力学正向解和反向解是一致的。
4 结论
通过对机械臂的静态力学分析,进行坐标转换,将机械臂在约束空间的动态模型转换为扩展空间的动态模型,针对机械臂系统的位置/力学建模分析,对重构的模型进行静态和动态分析,降低了优化后的机械臂结构的应力和应变,从而设计和优化六轴机械臂的平行牵引控制。在MATLAB Robotics 工具箱中建立模型,对机械臂的正向和反向运动力学问题进行求解和仿真,完成了机械臂的轨迹规划。仿真结果证明,联动六轴机械臂运动模型具有良好的运行稳定性,测试精度和误差范围都保持在较好的水平。该方法可应用于具有多自由度机械关节的机器臂,为今后不同复杂工况下的轨迹规划、离线编程和动态设计等研究奠定了基础,为机器人的广泛应用拓展了空间。
