某汽车分动器壳体辐射噪声分析及优化

杨镇，何锋，李家俊，陈飞

（1.550025 贵州省 贵阳市 贵州大学 机械工程学院；2.550025 贵州省 贵阳市 贵州华烽汽车零部件有限公司）

0 引言

分动器作为汽车传动系统的重要组成部分，其振动噪声问题不仅影响正常工作，还降低设备的疲劳寿命甚至影响环境[1-3]。分析分动器在无外界干扰条件下壳体简谐振动的辐射噪声、噪声来源及噪声频率对其降噪优化研究有着重要意义。

国内外学者针对壳体辐射噪声进行了研究。李玉光[4]等采用有限元与边界元联合求解研究高压油泵壳体表面辐射噪声特性，得出辐射声压云图，确定曲轴安装位置为主要的辐射噪声部位；Nandy[5]提出在轻密度流体中，壳体的固有频率大小会影响壳体的辐射噪声，且单纯的增加壳体的加强筋，有时会加剧壳体的振动水平；崔喆[6]等以封闭耦合壳体为研究对象，采用有限元和虚边界元以及最小二乘法求解壳体振动声辐射，最终得出，壳体壁厚、激励力位置等的变化对壳体声辐射有很大的影响；宋兆哲[7]等采用边界元法对发动机油底壳进行辐射噪声研究及壳体优化，指出增加壳体刚度和阻尼是减少表面振动的基本措施；Ide[8]等利用壳体优化方法使自动变速器辐射噪声和质量最小化，且考虑壳体弹性和声学的弱耦合评价壳体辐射噪声问题。因此，分析分动器壳体辐射噪声对于降低汽车传动系统乃至整车噪声具有实际意义。

为了降低分动器辐射噪声，本文基于模态叠加法及Helmholtz 波动方程对分动器壳体进行模态分析及简谐振动响应分析。将壳体振动响应特性作为壳体辐射声场的边界条件导入LMS Virtual.Lab 中，仿真得到壳体辐射噪声声场，分析该壳体的噪声分布，提出多种优化方案。

1 模态分析理论

模态分析理论是研究结构动态特性的主要方法之一，通过模态分析可以得到结构的固有频率以及振型。模态分析所对应的振动微分方程为

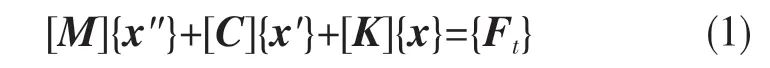
式中：[M]——质量矩阵；[C]——阻尼矩阵；[K]——刚度矩阵；{x}——位移矩阵。{Ft}——力矩阵。

Ft的物理意义为

转化为导数的形式：

该方程即为2 阶非齐次微分方程，求解时应假设{Ft}=0，将式（1）转化为齐次微分方程，并求解其特征根以及特征向量，得到的特征根按照从小到大顺序排列就是各阶的固有频率，对应的特征向量为各阶振型。

2 分动器有限元分析

2.1 网格划分

如图1 所示，建立有限元模型，对壳体连接处的紧固螺栓、电源接口、定位螺栓套筒及倒角进行简化。壳体材料选用A380，具体参数见表1。采用四面体网格划分，网格单元尺寸为4 mm。整体模型共有98 241 个节点、53 482 个单元。

图1 分动器模型Fig.1 Transfer model

表1 材料参数Tab.1 Material parameters

2.2 壳体载荷分布

分动器主要由电机、输入轴、输出轴以及各齿轮与定位轴承构成。图2 是分动器传动示意图。电机对齿轮1 施加转矩，驱动输入轴上的齿轮1 转动，通过轴承h 输出，各轴承孔将振动传递到壳体上。由于轴承受力过多，只提取输入轴的受力分析，如图2（b）所示。此壳体中，齿轮均采用直齿轮，因此将齿轮分度圆受力分解为径向力和圆周力，求解得轴承上的受力。

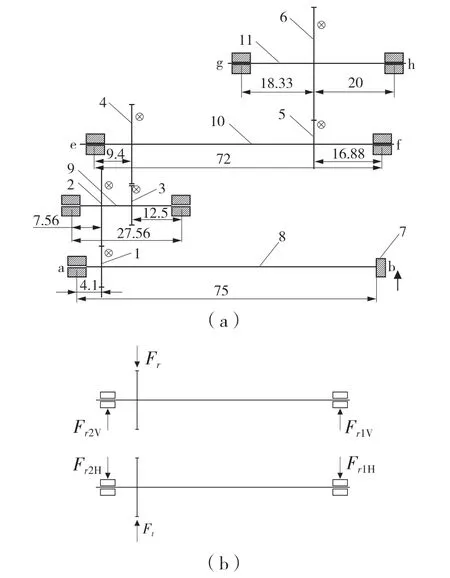
图2 分动器壳体传动示意图Fig.2 Transfer case transmission diagram

直齿圆柱齿轮的计算公式为：

式中：Ft——圆周力；T1——齿轮转矩；d——齿轮的分度圆直径；Fr——齿轮径向力；α——齿轮压力角；m——齿轮模数；z ——齿轮模数。

输出轴的最大承受转矩为5 N·m，根据表2齿轮参数及图2 分动器内部传动示意图可得壳体中各轴承的受力情况，见表3。

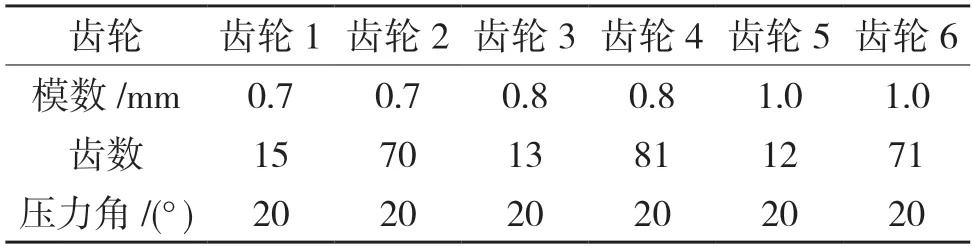
表2 齿轮参数Tab.2 Gear parameters

表3 轴承受力分析Tab.3 Bearing stress analysis

2.3 分动器简谐振动响应

求解壳体模态时，对2 个螺栓施加固定约束，忽略螺钉孔以及上下壳体所接触的表面摩擦。鉴于低阶模态对结构的动力学影响较大，取前6 阶模态进行分析，壳体各阶固有频率及振型见表4。分动器各阶的固有频率主要集中在1 419.4～4 719 Hz，且模态振型主要以弯曲、扭转变形为主。

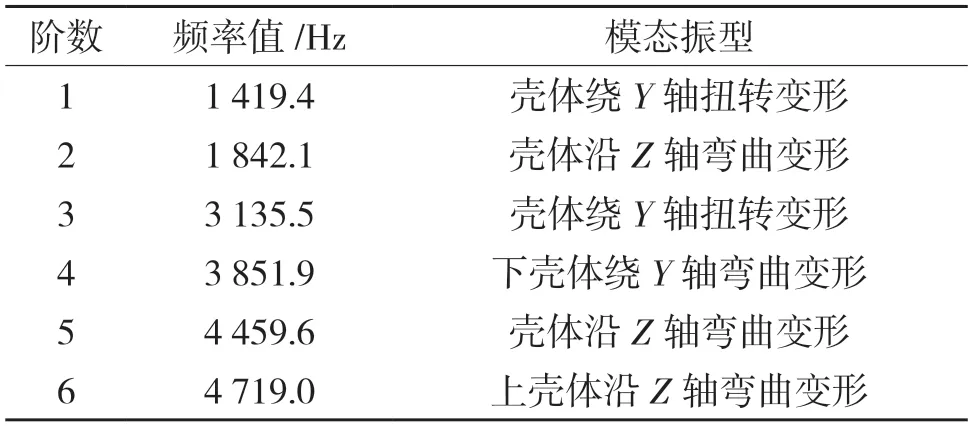
表4 壳体模态分析Tab.4 Shell modal analysis

前6 阶模态振型如图3 所示。分动器的振动变形主要集中在上壳体的顶部、下壳体的输出轴承口壳体表面，对于壳体表面的振动速度与辐射噪声之间存在着一定的比例关系[9-10]，因此对壳体进行优化时，可考虑对此进行优化，以减少其振动幅值。

图3 分动器前6 阶模态振型Fig.3 First six order modal shapes of transfer case

确定壳体模态振型后，结合分动器实际工作情况对壳体进行振动响应分析。在壳体内部的各轴承孔上施加与表3 中对应大小的力，将运行求解最大频率设置为6 000 Hz，求解步长为60 Hz。基于上述前6 阶模态振型得到分动器在X 轴、Y 轴、Z 轴方向振动响应曲线如图4 所示。

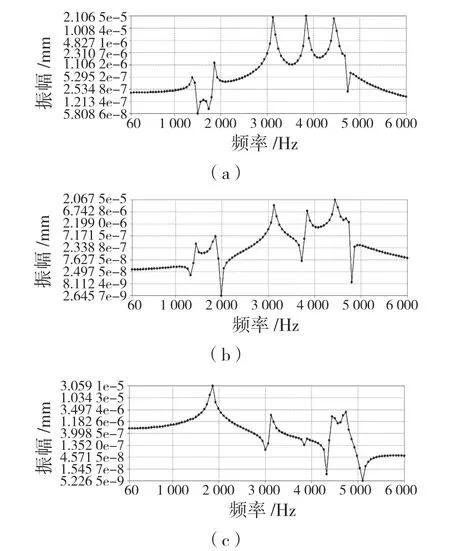
图4 分动器振动响应分析结果Fig.4 Coupling vibration response analysis results of transfer case

由图4 知，在1 860，3 120，3 840，4 440 Hz及其他峰值频率均为分动器壳体的临界频率，机构产生明显振动。分动器壳体在1 860，3 120，3 840，4 440 Hz 产生最大位移振幅。其中1 860 Hz 与2 阶固有频率1 842.1 Hz 相近，故发生共振，产生较大峰值。图4（a）中，X 方向振动位移幅值发生在3 840 Hz，幅值为2.106 5×10-5mm；Y 方向振动位移幅值发生在4 440 Hz，幅值为2.067 5×10-5mm；Z 方向振动位移幅值发生在1 860 Hz，幅值为3.065 91×10-5mm。

2.4 分动器辐射声场分析

将分动器模型导入LMS Virtual.lab 进行声学网格划分。声学网格的大小由求解频率以及流体属性决定，最大单元边长要求小于计算频率最短波长1/6，或小于最高计算频率点处波长的1/6[11]。即：

式中：λ——网格尺寸大小；c——理想空气下的声速；fmax——声学求解的最大频率。

求解的最大频率6 000 Hz，声速340 m/s，密度1.225 kg/m3，得声学网格最大尺寸为9.44 mm。声学网格细化对分析精度提升不大，因此网格尺寸取5 mm，网格节点数9 950，单元数19 900。将振动响应特性导入声学边界元，转移其属性到声学网格，由于声学网格与壳体网格不匹配，通过点之间加权计算后转移到声学网格，作为分动器声学求解边界。利用场点网格模拟辐射噪声外声场，在距分动器中心400 mm 处建立圆形声场网格。设置求解最大频率为6 000 Hz，取步长为60 Hz。分动器最大负载转矩下辐射噪声声压云图如图5 所示。

图5 分动器声压云图Fig.5 Sound pressure cloud diagram of transfer case

图5 中分动器表面辐射噪声声压在1 840，3 160，3 880，4 420 Hz 处存在较大声压级，壳体最大声压值分别为63.2，68.9，69.0，81.6 dB。声压最大值主要集中在壳体下壳体输出轴承口所在面及分动器上壳体顶部，因此下壳体输出轴承口所在面以及分动器上壳体顶部是噪声的主要来源，考虑分动器实际装配条件，进行壳体降噪优化时主要针对壳体的下壳体进行优化。

3 分动器降噪优化

增加壳体刚度是减少壳体自由振动的基本措施，在同样激振力作用下减少壳体表面振动响应可使噪声降低。即改变分动器输出轴承口表面厚度并布置加强筋[12-13]，根据以上分析，对分动器下壳体优化方案如图6 所示。

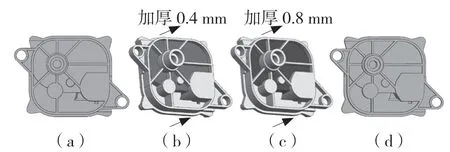
图6 优化方案Fig.6 Optimization scheme

与原模型相比，主要做出以下改变：

（1）增加壳体的厚度。增加厚度位置为输出轴承口所在壳体表面，为了分析厚度对壳体噪声的影响，分别增加0.1，0.2，0.4，0.6，0.8 mm（原厚度为3.2 mm）如图6（b）、图6（c）所示。

（2）增加加强筋。在下壳体表面增加加强筋，固定齿圈以及下壳体边缘横条，加强筋宽度为3.1 mm，长度20.3 mm，高度8.6 mm，如图6（d）所示。上述方案在约束、受力、材料等与原模型一致的条件下，求解各方案的固有频率，对比优化前后各阶固有频率如表5 所示。

表5 优化前后固有频率对比Tab.5 Comparison of natural frequencies before and after optimization

相较原方案，3 个优化方案低阶固有频率基本一致，高阶模态振型下的固有频率有所增加。另外，在对下壳体进行加筋以及加厚以后，壳体质量分别在原方案916.53 g 的基础上增加了0.64%、1.2%、0.16%，壳体质量增量较小，提升了壳体的刚度，降低了壳体振动。

优化后的各方案分别取节点110 793，110 836，110 882，110 959 的平均声压级曲线，并通过与原方案声压级曲线进行对比得到图7。由图7 可知，方案1 在中、低阶频率段内优化效果较好。相较于原方案声压级曲线的各处峰值均有所减小。原方案在1 840，3 160，3 820，4 420，4 660 Hz产生峰值声压，对应的峰值声压分别为58.860 0，63.237 5，61.890 0，74.360 0，73.055 0 dB。方案1对应声压分别为56.805 0，63.312 5，55.850 0，62.092 5，54.512 5 dB，分别下降 了2.055 0，-0.075 0，6.040 0，11.435 0，18.542 5 dB。且方案1 在4 480 Hz 以前产生的各处峰值声压在优化后均有所降低，优化效果较好。方案2 较原方案固有频率增加，分动器壳体的刚度增加，在低阶频率段内实现了较小的降噪，但3 160 Hz 开始，多处产生较原方案较大峰值声压，整体优化效果较差。方案3 在高阶频率段4 660～6 000 Hz 内优化效果较好，最大降低了13.245 dB。中、低阶频率段内的优化效果较差，原方案各处峰值声压优化后并没有实现峰值降低，且在4 480 Hz 处产生3 个方案中最大峰值84.795 dB，方案3整体优化效果一般。

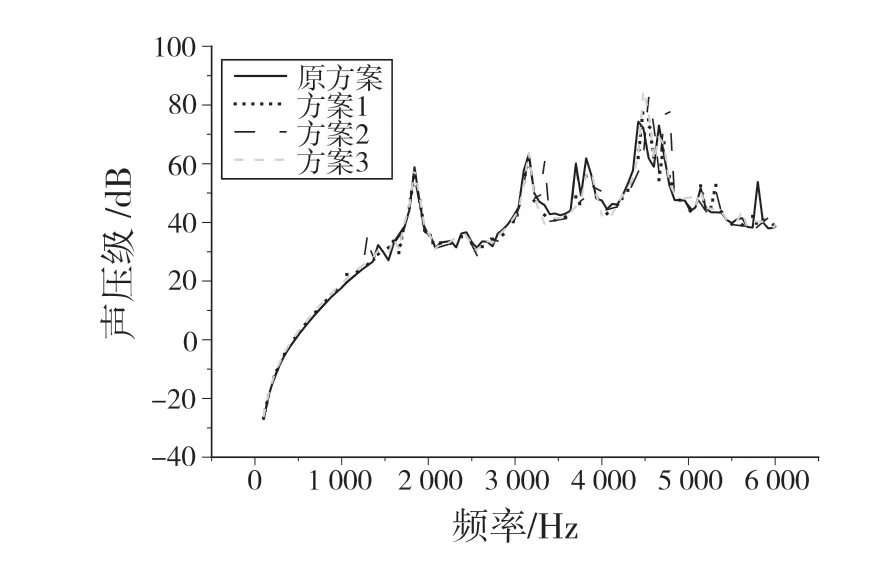
图7 各方案声压级曲线对比Fig.7 Comparison of SPL curves of different schemes

综合以上3 种方案，方案1～方案3 在原方案基础上固有频率、质量均有所增加，一定程度上提高了分动器的局部强度，而质量有一定提高，但是提高较小，所以整体而言达到了优化效果。其中，方案1 的降噪优化效果较好，不仅对分动器中、低阶频率段内有着较好的降噪效果，而且提高了机构的刚度，增加了分动器运行时的可靠性，且各处峰值声压在原方案的基础上也有一定程度优化。加厚方案中，通常是依据经验加厚0.4 mm、0.8 mm，其产生的降噪效果与增加壳体厚度并非成正比关系，虽然一定程度上能达到预期的优化效果，但适用范围较窄，仅适用于某些要求精度不高的场合。

4 结论

通过有限元和边界元的方法对分动器辐射声场进行分析，结合壳体的模态振型以及声压云图提出壳体优化措施，分别对下壳体增加加强筋及齿圈所在表面加厚0.4 mm 和0.8 mm，通过声压级曲线对比，得出如下结论：

（1）对分动器下壳体加厚0.4 mm方案（方案1）最佳，在中、低阶频率段内有效降低壳体的辐射噪声，较于原方案各处峰值声压有一定的优化效果；

（2）下壳体振动处增加加强筋及壳体厚度可提升壳体的固有频率和刚度，有效抑制下壳体的振动强度，但单纯增加固有频率，其降噪效果可能得不到改善。