基于GTN模型的小冲孔高温拉伸性能表征

赵 雷，王 逊，徐连勇，韩永典

基于GTN模型的小冲孔高温拉伸性能表征

赵 雷，王 逊，徐连勇，韩永典

(天津大学材料科学与工程学院，天津 300072)

由于常规高温性能测试试验时间周期长，而小冲孔试验简单便捷，并且更适用于微小对象的研究．本文针对新型奥氏体耐热钢Sanicro25，进行了不同速率下小冲孔高温拉伸试验，提出了新的抗拉强度计算公式，计算精度高；观察小冲孔试样扫描电镜断口形貌，发现主要是韧性断裂形式，和单轴拉伸结果相似；采用ABAQUS软件结合适用于金属韧性断裂损伤的Gurson-Tvergaard-Needleman(GTN)模型对小冲孔拉伸过程进行了数值分析，采用分段优化和最小二乘法等获得了改进的GTN模型的不同参数值，最终模拟结果与试验结果相近；在对小冲孔变形过程分析中，提出了GTN模型中临界空隙体积分数与断裂体积分数和最大载荷及其位移的定性关系．

小冲孔测试；有限元；GTN模型；载荷-位移曲线

将试验对象制成直径3～10mm、厚度在0.25～0.50mm薄片的小冲孔法，具有研究对象小、试验周期短的特点，适用于研究微区结构或薄壁复杂结构的性能，可有效解决由于材料尺寸限制导致无法制备标准单轴试样的问题[1-3]，因此在研究焊接接头等复杂或薄壁结构中具有广泛的应用前景[4]．2010年前后，国外提出了小冲孔法性能测试标准[5]，标准中采用冲孔和单轴试验结合的方法，将两者结果利用经验转换公式计算材料性能，其过程繁复，周期长．Peter等[6]直接利用小冲孔试验结果计算了材料屈服强度，Holmström等[7]利用膜应力公式和经验公式建立了小冲孔抗拉强度计算公式，并且具有较好的准确性．这些研究多数在常温下进行，而对于服役于高温应力环境下的材料，其公式的适用性有待验证．另外，结合有限元模拟的方法可以进一步研究小冲孔的变形过程和各项材料性能[8-9]．

考虑到小冲孔高温拉伸过程主要是韧性断裂控制，而Gurson-Tvergaard-Needleman(GTN)模型主要用于分析金属韧性断裂过程和韧性损伤模拟．Liu 等[10]利用GTN模型模拟含Mn-S夹杂物钢的高温失效行为，为研究钢材高温问题提供新方法；Guo等[11]利用GTN模型对9Cr/CrMoV钢的焊接接头的不同区域进行了裂纹扩展模拟，为预测接头裂纹扩展失效提供方法；针对GTN模型中的空隙体积分数，Wcislik[12]对一种材料临界空隙体积分数做了试验测定．而Chen等[13]提出一种新的GTN模型空隙体积分数的表达式，该表达式更加适用于三轴应力状态的模拟．Li等[14]则利用该体积分数研究306L钢小冲孔常温拉伸，并对拉伸曲线进行拟合，模拟与实际结果相符．然而结合GTN模型研究小冲孔高温拉伸过程鲜有报道，小冲孔变形过程与常规单轴拉伸大不相同，使得采用GTN模型的模拟小冲孔变形变得更加困难．

因此，本文对比研究小冲孔法和单轴法对材料高温拉伸力学性能的影响，建立高温下小冲孔拉伸模型．以700℃Sanicro25钢小冲孔拉伸试验数据，获得其载荷-位移曲线与微观形貌，与单轴高温拉伸数据对比，利用提出的改进公式，计算得到700℃下Sanicro25钢高温屈服强度和抗拉强度．采用有限元方法利用建立带有分段空隙体积分数的GTN损伤模型，模拟试样变形过程，确定了合适参数值，并提出了空隙体积分数与曲线极值点的关系式．

1 试验及模型

1.1 小冲孔试验

本文研究新型奥氏体耐热钢Sanicro25钢的高温力学性能，Sanicro25钢由于优异的抗氧化性能和蠕变性能，是630～650℃新一代超超临界火电机组的受热面钢以及高温过热再热器备选材料．本文管道外径为60mm，壁厚12mm，供货状态是冷轧＋固溶处理，其化学成分如表1所示．小冲孔拉伸试验机采用ZRWS-K1试验机，装置示意如图1所示．夹具下模具孔为2mm，冲球半径为1.25mm．通过控制冲头下降速度来控制试样应变速率，加载速率为0.1mm/min和1.0mm/min，试验温度为700℃．

表1 Sanicro25 钢化学成分

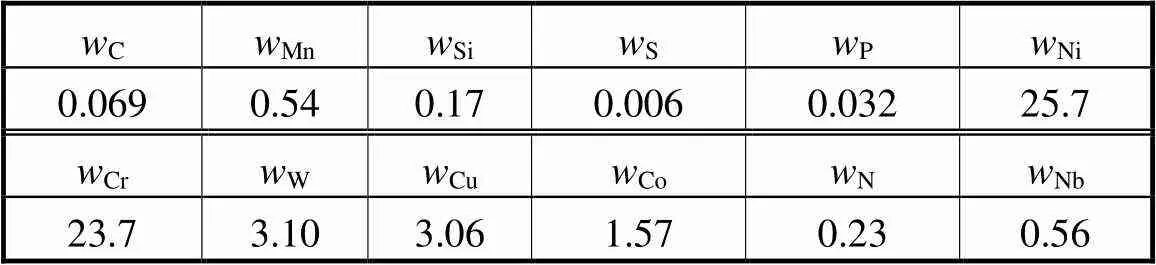
Tab.1 Chemical composition of Sanicro25 steel %

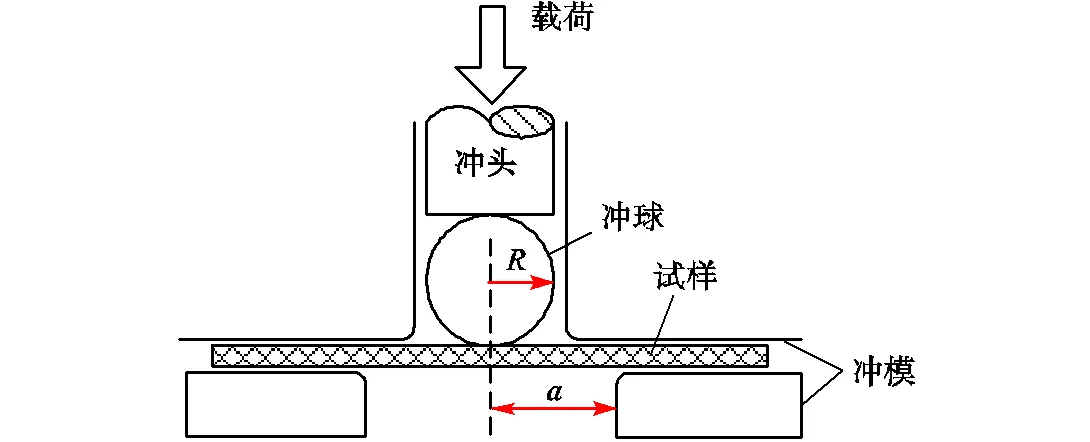
图1 小冲孔装置示意

1.2 GTN模型

为了分析Sanicro25钢小冲孔变形过程中应力和应变演变情况，结合GTN模型对小冲孔过程塑形失效进行分析．小冲孔变形过程中载荷-位移曲线如图2所示，可分为5个阶段．第1、2阶段中小冲孔变形主要受弹塑性参数影响，分别为弹性模量、泊松比、塑形硬化行为和．第3、4、5阶段中，韧性损伤起主导作用，即由GTN损伤模型控制，参数分别为初始空隙体积分数0、空隙形核粒子体积分数N、临界空隙体积分数c和最终失效空隙体积分数F．而考虑空隙体积分数的GTN模型为

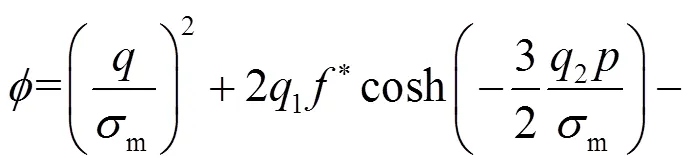
(1)

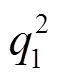
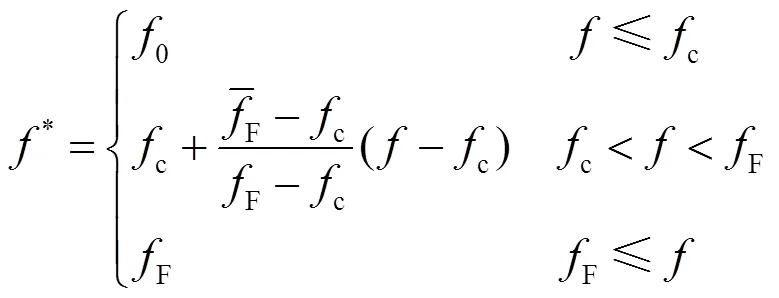
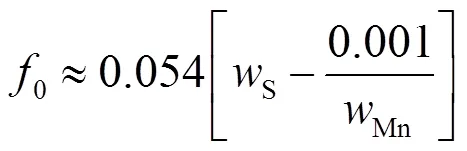
而当空隙体积分数增长超过临界空隙体积分数c时，空隙开始大量增殖，并产生新的空隙，而新空隙体积分数的增加为

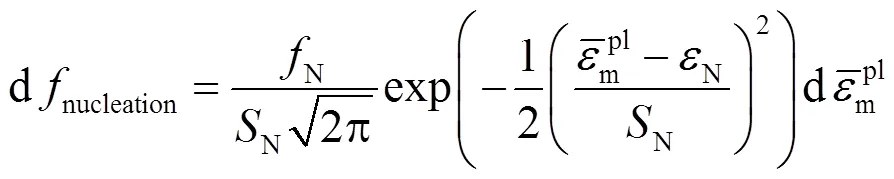
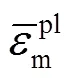
对于不同材料GTN模型参数1、2、3、N和N分别等于1.5、1.0、2.25、0.2和0.1时，拉伸曲线和测试曲线拟合效果更好，因此本文采用相同的模型参数．大量的试验[14]表明N、c、F的取值范围分别是0.004～0.050、0.02～0.20和0.10～0.30．

1.3 有限元模型

本文采用ABAQUS软件模拟分析Sanicro25钢小冲孔高温拉伸过程，有限元模型和网格划分如图3所示，采用二维轴对称模型．网格尺寸为0.25mm×0.25mm．该尺寸可以精确模拟薄片变形行为，并且选用更小的尺寸网格不影响数值计算结果．

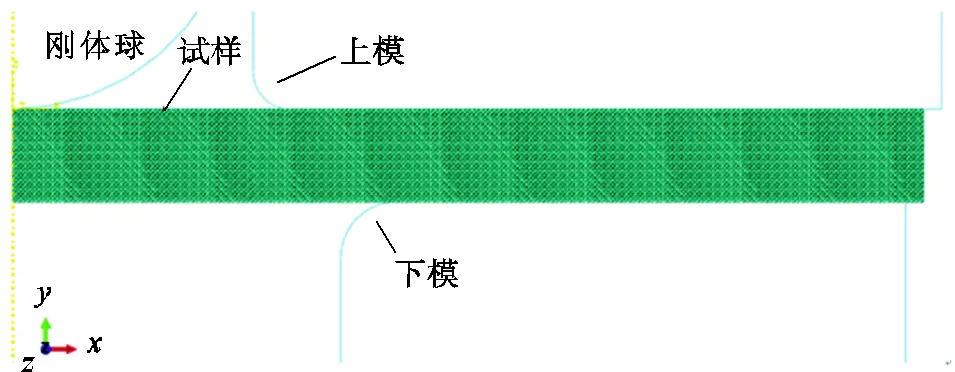
图3 Sanicro25钢小冲孔变形有限元模型及网格划分

2 结果与分析

2.1 Sanicro25钢高温拉伸性能分析

图4为两个应变速率下4个Sanicro25钢试样在700℃下小冲孔试验测得的位移与载荷的关系．表2为采用标准试样测试的700℃下Sanicro25钢力学性能．峰值载荷和峰值变形位置如图4所示，从图4中可以明显看出随着薄片变形的增大，即位移增大，载荷值呈现先增加后下降的趋势．而且小冲孔试样变形过程中同样存在材料的弹性变形、屈服拉伸、应变硬化等现象，但无法直接从载荷-位移曲线中获得材料的力学性能．小冲孔方法测量的材料屈服强度主要取决于弹塑性转变载荷，屈服强度计算式[15]为

式中：Rp0.2为屈服强度；Fe为试验弹塑转变载荷；a 为与材料种类有关的常量系数；t为初始试样厚度．Sanicro25钢属于奥氏体合金钢，而通常的奥氏体合金钢的a 的取值为0.33[8]．采用Mao等[16]法得到转变载荷Fe，如图5所示．

表2 单轴条件下Sanicro25钢高温拉伸力学性能[17]

Tab.2 High-temperature tensile mechanical properties of Sanicro25 under uniaxial conditions[17]

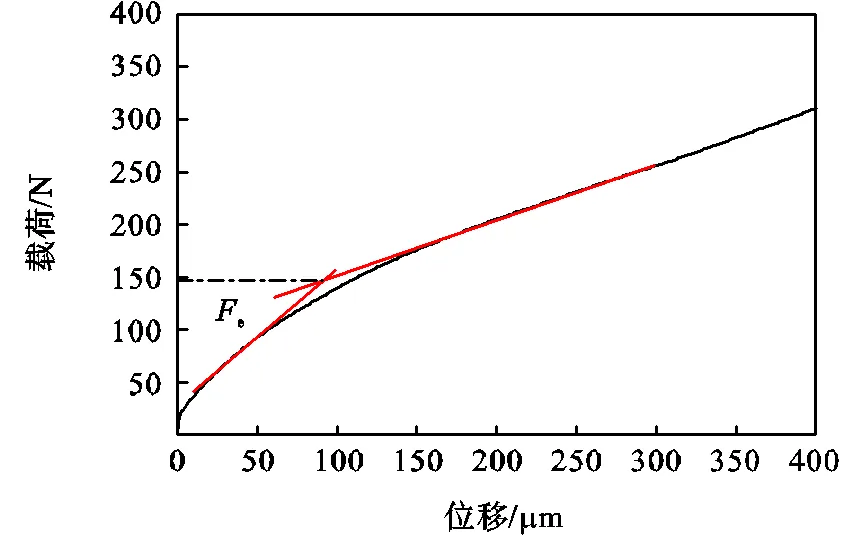
图5 试样1转变载荷Fe

小冲孔法测试过程中抗拉强度也是由所承受的最大载荷决定，小冲孔试验过程中同样存在与单轴拉伸过程类似的超过最大载荷后试样并未立即断裂的现象．因此小冲孔试样处于最大载荷处变形如图6所示，根据膜应力理论，可计算材料的抗拉强度m1.

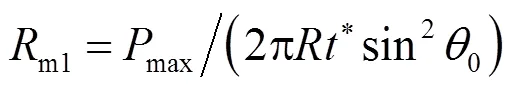
式中：m1为抗拉强度；max为最大载荷值；0为试样初始厚度；*的计算式为

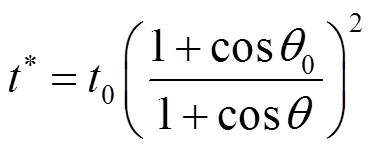
而与0的关系可以由式(8)和式(9)计算得到.

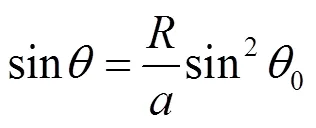
式(6)为根据文献[18]研究不同金属材料的小冲孔拉伸测得的抗拉强度的经典数值拟合公式(如式(10)所示)，并借鉴文献[19]提出的改进公式．

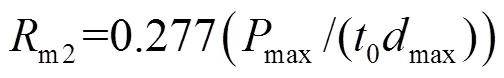
考虑实际最大拉伸位置处的薄膜厚度为min，因此由图6(b)得出式(11)从而替代式(8)，最后解出min代替*，将膜应力公式与数值拟合公式结合，提出式(12)．

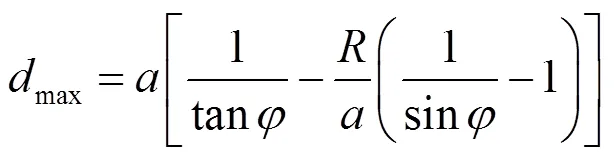
(12)

采用图4中试验曲线及结果，计算两组应变速率下屈服强度以及3个公式计算的抗拉强度结果如表3所示，膜应力式(6)计算得到的抗拉强度明显高于单轴试验结果，最大误差达68%．这可能由于膜应力理论中未考虑摩擦因素、不同材料的硬化方式以及高温环境的影响，数值拟合式(10)是通过将不同材料的小冲孔试验数据与单轴拉伸数据提出的线性拟合关系式，不具有较强的物理意义，且在大应变速率下计算误差较大，达11%．本文提出的小冲孔抗拉强度公式(12)是在膜应力和数值拟合的基础上，将两者结合，考虑在拉伸过程中最大载荷处的位移值、冲球半径对试样厚度变化的影响，具备一定的物理意义．从计算结果上看，本文提出的公式提高了计算结果的准确性，误差均在6%以内，在不同应变速率下的计算结果有良好的稳定性．综合考虑3种方法结果可以得出，速率为0.1mm/min的试样1的抗拉强度计算结果稳定，并且误差较小，以此试样的条件和结果为基础，进行小冲孔建模的参数分析和计算．

表3 700℃ Sanicro25钢不同速率下小冲孔力学性能结果

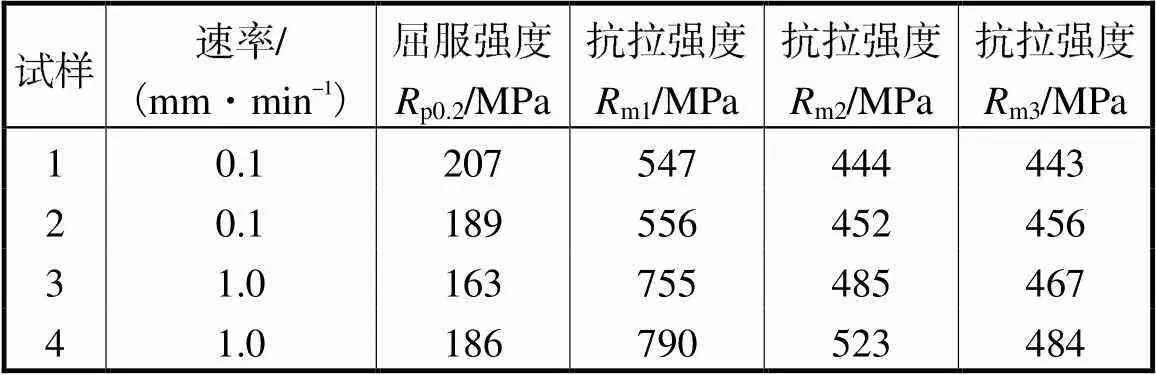
Tab.3 Calculated mechanical properties of small punch tests at different rates for Sanicro25 steel at 700 ℃

Sanicro25钢小冲孔试样断口微观组织形貌如图7所示，图7(a)为Sanicro25钢小冲孔高温拉伸断裂失效的整体形貌，图7(b)为断口处的局部形貌．从图中可以看出断口上、下表面深裂痕是由于试样变形的应力集中所致，断口内部中充满着大量的撕裂楞和韧窝，这是典型的延性断裂的断裂形式，这表明Sanicro25钢在700℃拉伸失效的失效形式是延性断裂，并且从图7中可以看出，在韧窝和撕裂楞附近存在少量微小空洞，与GTN模型由空洞控制的损伤和断裂过程也相一致．

图7 小冲孔试样断裂失效形貌

3 Sanicro25钢小冲孔高温拉伸有限元分析

Sanicro25钢GTN模型中弹塑性变形参数是由700℃单轴拉伸应力-应变曲线所确定．建立Sanicro25钢的弹塑性变形段的模型曲线与试验结果对比，如图8所示．从图中可以看出，模拟和试验结果的误差随着位移增加而增大，这是由于变形导致的空隙体积增大所引起的误差．

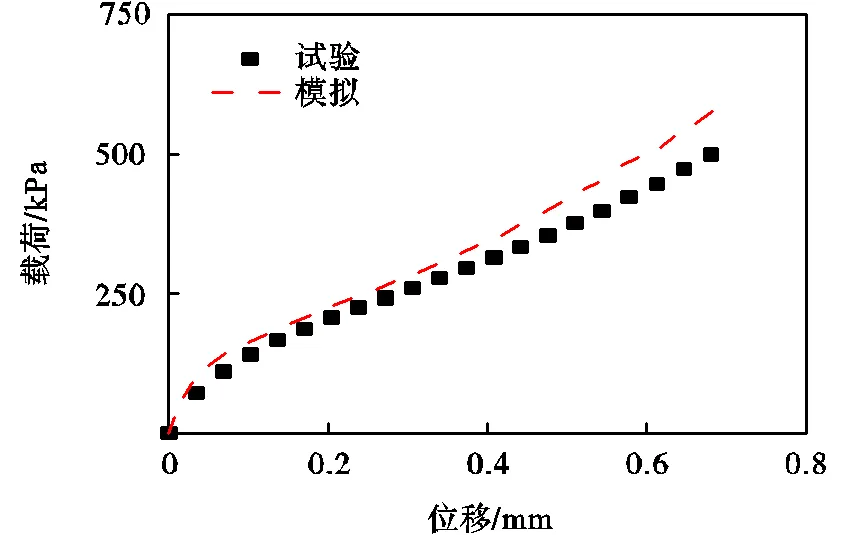
图8 第1、2阶段模拟结果与试验结果

GTN损伤模型中空隙体积分数参数包括有初始空隙体积分数0、空隙形核粒子体积分数N、临界空隙体积分数c以及最终失效空隙体积分数F．初始空隙体积分数0可由测定的Sanicro25元素含量代入式(3)可得，计算为0.000224．空隙形核粒子体积分数N在载荷-位移曲线的第3阶段起着主导作用，如图9所示．从图中可以看出，第3阶段的曲线呈线性，可由＝＋对载荷进行线性表示，其中表示位移，、是线性拟合系数．N与、仍呈现线性关系，如图10所示，最后得到N、与的关系，即

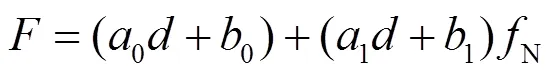
式中0、1、0、1均为相关系数，拟合运算可得其值如表4所示．

表4 式(13)中的线性参数值

Tab.4 Linear parameter values in Eq. (13)

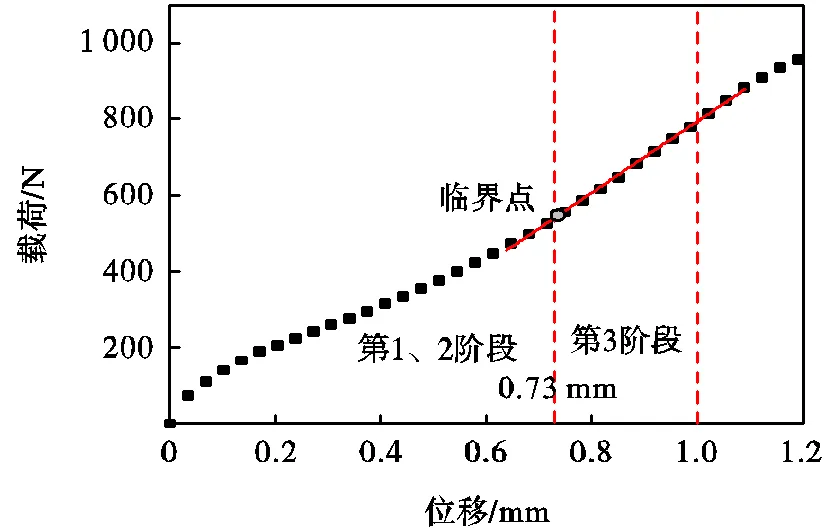
图9 载荷-位移曲线第3阶段线性关系

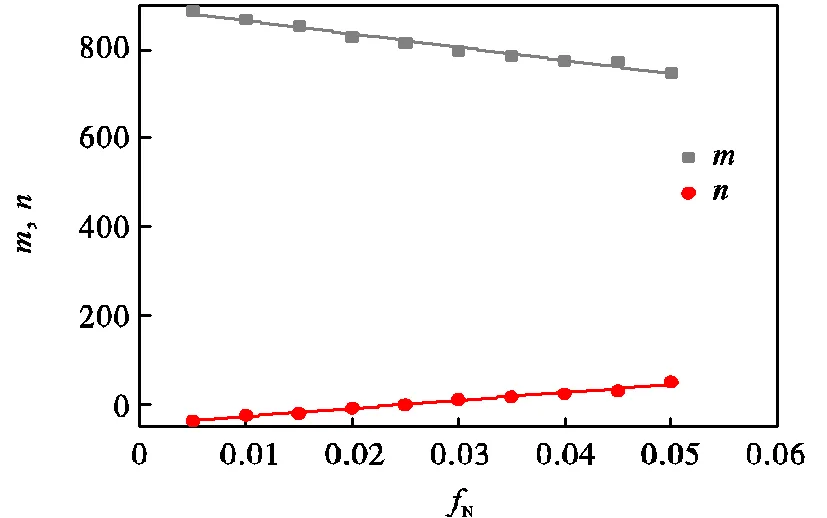
图10 不同fN下m、n的关系

将得到的线性参数值代入式(13)，并选个试验的位移值，计算得到相同位移下的载荷值，记为cal，利用式(14)计算误差值error，选取误差最小的N作为最适值．

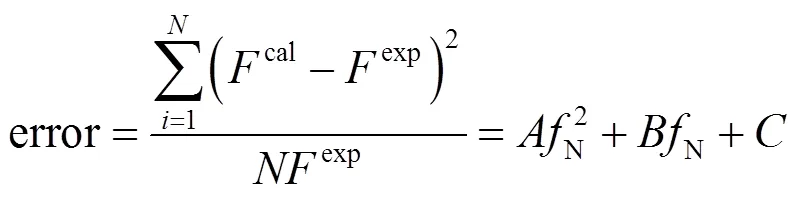
式中、、为相关系数，根据试验所得数据分别计算所得参数值如表5所示．由计算所得最优N为0.039.

表5 式(14)中的参数值

Tab.5 Parameter values in Eq. (14)

c和F共同作用于曲线第4、5阶段，影响最大载荷值及其位移，根据c和F的取值范围，进行等分取值模拟，发现模拟结果中最大载荷max及其位移max与F和c满足式(15)，其计算值与模拟值关系如图11所示．其中表示最大载荷值和该载荷下的位移，1～4取值如表6所示．

最大载荷和位移平均误差分别为2%和3%．试验得到的最大载荷及其位移分别为963N和1.2mm，代入式(15)计算得到的fc和fF分别为0.0051和0.4239，可见fc与fF均不在预设的可取值范围内，因此模拟误差较大，如图12所示．

表6 空隙体积分数与曲线极值点关系式(15)的参数

Tab.6 Parameters of Eq.(15) between the void volume fraction and the extreme point of the curve

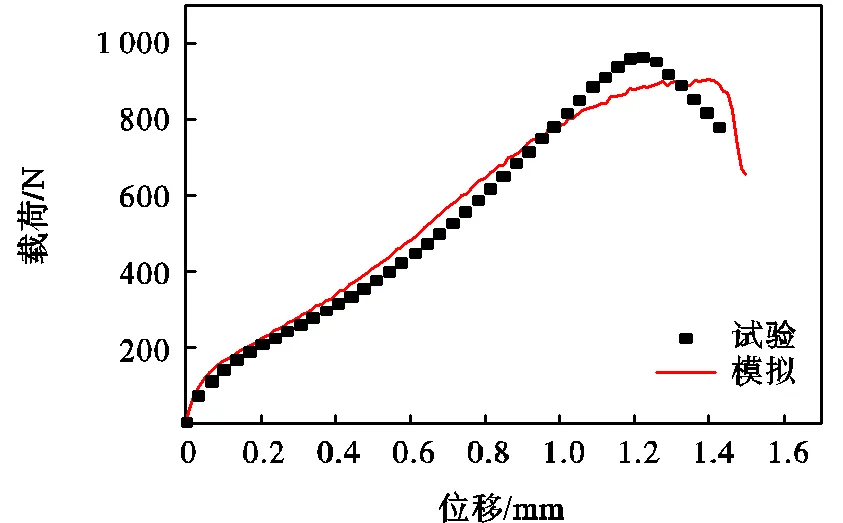
图12 计算得到fc与fF模拟结果

考虑试验曲线与模拟曲线在位移为1.0mm的点出现偏离，即此处孔隙开始聚集，如图13(a)所示，因而位移为1.0mm处的空隙体积分数即为参数临界空隙体积分数c的值．而位移为1.25mm是试验曲线的拐点，即为第3阶段和第4阶段的分割点，位移为1.25mm时的试样下表面节点的空隙体积分数随对称轴线的距离的变化如图13(b)所示．从中可以看出，距轴线0.8mm处的节点空隙体积分数最大，而此节点属于7002单元，7002单元空隙体积分数随位移的变化曲线如图13(c)所示．由图可知，7002单元在位移为1.0mm的空隙体积分数为0.0843，即为c＝0.0843．

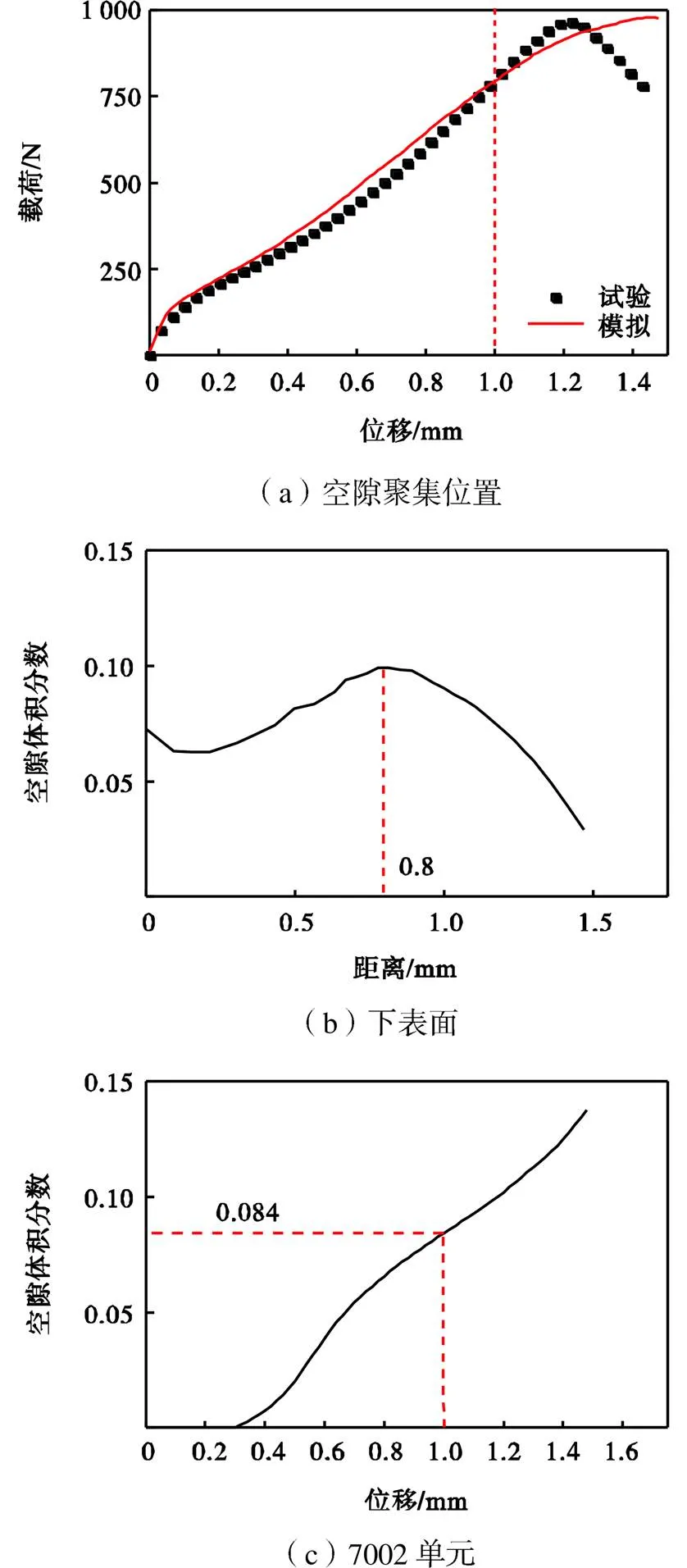
图13 临界空隙体积分数fc的确定

F作用于曲线第5阶段，影响最大载荷值，由F的取值范围，设置0.10、0.20、0.30，并采用二分法，如图14所示，从图中可以看出，F＝0.26时，拟合效果更好．将参数优化后有限元计算的曲线和试验结果进行对比，如图15所示．考虑到弹塑性-损伤模型的模拟结果与试验数据的变形趋势一致，其最大载荷位置大致相同，偏差不超过6%．因此可以按照带有空隙体积分数参数的GTN损伤模型建立的高温小冲孔试验模型能够较为准确地模拟Sanicro25钢在700℃下小冲孔法的高温拉伸过程．

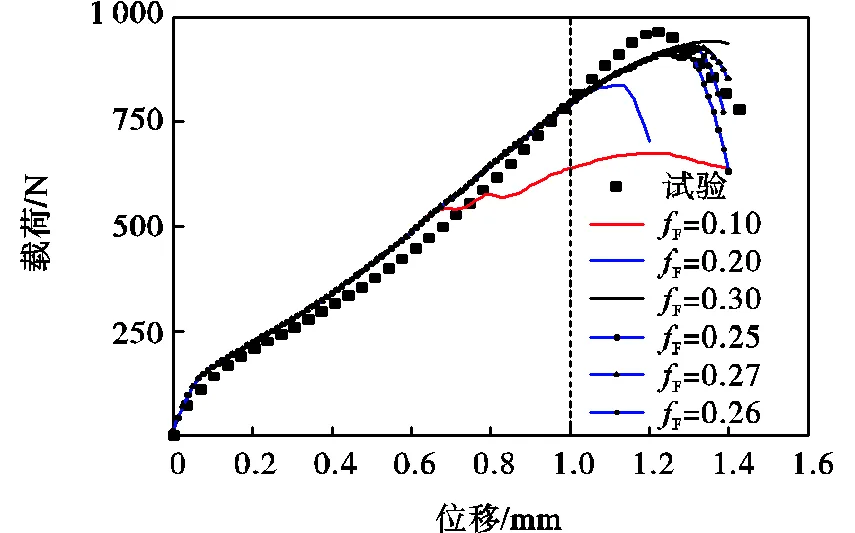
图14 不同fF值下的模拟

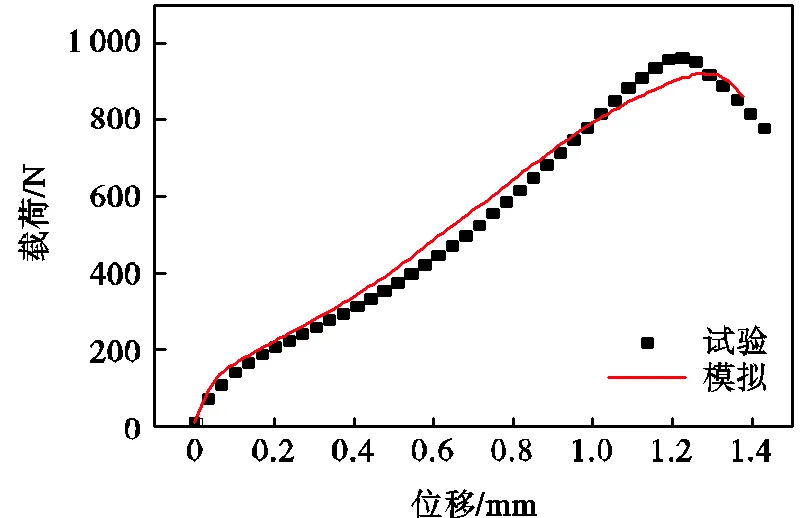
图15 小冲孔变形有限元模拟

对有限元模拟所得载荷-位移曲线进行强度分析，可得模拟曲线的转变载荷e为141N，由式(5)计算可得屈服强度为185MPa，与小冲孔拉伸试验值相差11%，与单轴拉伸试验值相差17.4%．有限元模拟的载荷最大位移为1.26mm，最大载荷为920N，因此由式(10)和式(12)可以计算出Sanciro25钢模拟抗拉强度通为404MPa，与小冲孔拉伸试验值相差7.8%，与单轴拉伸试验值相差14%，模拟结果的力学性能与实际测试结果相差不大，因此采用带有空隙体积分数的GTN有限元模型对高温条件下小冲孔拉伸模拟具有良好的适用性．

4 结 论

本文以Sanicro25钢700℃小冲孔拉伸为基础，研究小冲孔法对材料拉伸性能影响，提出了小冲孔抗拉强度计算公式，并建立小冲孔高温拉伸-GTN损伤模型，分段考虑其参数对载荷-位移曲线影响，得到的结果与实际较为接近，结论如下.

(1) 结合膜应力公式和数值拟合公式，本文提出的抗拉强度计算公式，在不同应变速率下700℃Sanicro25钢的小冲孔抗拉强度的计算中具有更好的准确性，误差提高至6%以内．

(2) 通过断口扫面电镜下出现大量韧窝组织，与单轴结果吻合，证实小冲孔法研究塑性材料高温强度性能的科学性和可行性；观察到小冲孔试样断口内存在少量微小空洞，因此模拟Sanicro25钢的小冲孔高温拉伸所采用的GTN损伤模型要考虑到空隙体积分数对模拟结果的影响．

(3) 通过分段优化模拟和数学拟合方法，得到了Sanicro25钢700℃小冲孔高温拉伸模型的各参数值，并提出了GTN空隙体积模型参数c和F与试验曲线最大载荷值max及其位移max的关系式．

［1］ Rodriguez C，Fernandez M，Cabezas J，et al. The use of the small punch test to solve practical engineering problems[J]. Theoretical and Applied Fracture Mechanics，2016，86：109-116.

［2］ 荆洪阳，苗春龙，徐连勇，等. 港口机械超大型构件焊接顺序规划研究[J]. 天津大学学报(自然科学与工程技术版)，2021，54(4)：435-440.

Jing Hongyang，Miao Chunlong，Xu Lianyong，et al. Welding sequence planning for port machinery large welded structures[J]. Journal of Tianjin University (Science and Technology)，2021，54(4)：435-440 (in Chinese).

［3］ 徐连勇. 长寿命高可靠性焊接结构[J]. 天津大学学报(自然科学与工程技术版)，2022，55(1)：1-10.

Xu Lianyong. Long-lift and high-reliability welded structure[J]. Journal of Tianjin University(Science and Technology)，2022，55(1)：1-10(in Chinese).

［4］ Zhao Lei，Jing Hongyang，Xu Lianyong，et al. Evaluating of creep property of distinct zones in P92 steel welded joint by small punch creep test[J]. Materials and Design，2013，47：677-686.

［5］ BSI CWA 15627—2007 Small Punch Test Method for Metallic Materials[S]. Europe，CEN Workshop Agreement，2007.

［6］ Peter H，Celal S，Betül G C，et al. Determining tensile yield stresses from small punch tests：A numerical-based scheme[J]. Materials and Design，2019，182：1-11.

［7］ Holmström S，Simonovski I，Baraldi D，et al. Developments in the estimation of tensile strength by small punch testing[J]. Theoretical and Applied Fracture Mechanics，2019，101：25-34.

［8］ Ha J S，Fleury E. Small punch tests to estimate the mechanical properties of steels for steam power plant：Ⅱ. Fracture toughness[J]. International Journal of Pressure Vessels and Piping，1998，75(9)：701-713.

［9］ Abendroth M，Kuna M. Determination of deformation and failure properties of ductile materials by means of the small punch test and networks[J]. Computainal Materials Science，2003，28(3/4)：633-644.

［10］ Liu X G，Wang C，Feng Q，et al. High-temperature fracture behavior of MnS inclusions based on GTN model[J]. Journal of Iron and Steel Research International，2019(9)：941-952.

［11］ Guo Q，Lua F G，Cui H C. Modelling the crack propagation behavior in 9Cr/CrMoV welds[J]. Journal of Materials Processing Technology，2015，226：125-133.

［12］ Wcislik W. Experimental determination of critical void volume fractionFfor the Gurson Tvergaard Needleman (GTN) model[J]. Procedia Structural Integrity，2016，2：1676-1683.

［13］ Chen Z T，Datta R A. Stress-state related void coalescence criterion and its validation[J]. Mechanics and Materials，2011，1082(44/45/46/47)：2656-2660.

［14］ Li K S，Peng J，Zhou C Y. Construction of whole stress-strain curve by small punch test and inverse finite element[J]. Results in Physics，2018，11：440-448.

［15］ Chica J C，Díez P M B，Calzada M P. Development of an improved prediction method for the yield strength of steel alloys in the small punch test[J]. Materials and Design，2018，148：153-166.

［16］ Mao X Y，Takahashi H. Development of a further-miniaturized specimen of 3 mm diameter for TEM disk (3mm) small punch tests[J]. Journal of Nuclear Materials，1987，150(1)：42-52.

［17］ Zhang Y，Jing H，Xu L，et al. Microstructure and texture study on an advanced heat-resistant alloy during creep[J]. Materials Characterization，2017，130：156-172.

［18］ Dobeš F，Dymáček P，Besterci M. Estimation of the mechanical properties of aluminium and an aluminium composite after equal channel angular pressing by means of the small punch test[J]. Materials Science & Engineering A，2015，626：313-321.

［19］ Zhao Lei，Song Kai，Xu Lianyong，et al. Determination of creep properties of an advanced Fe-Cr-Ni alloy using small punch creep test with a modified creep strain model[J]. Theoretical and Applied Fracture Mechanics，2019，104：102324.

Characterization of High-Temperature Tensile Properties of Small Punch Test Based on the GTN Model

Zhao Lei，Wang Xun，Xu Lianyong，Han Yongdian

(School of Materials Science and Engineering，Tianjin University，Tianjin 300072，China)

Due to the long testing time of the conventional high-temperature performance test，the small punch test is convenient and more suitable for the study of mini objects. In this study，a new type of austenitic heat-resistant steel，Sanicro25，was developed for high-temperature tensile tests via small punch tests at different rates. A new formula for calculating tensile strength with high accuracy is proposed. The fracture morphology of the small-punch specimen was observed via scanning electron microscopy. It was found that the ductile fracture was similar to the uniaxial tensile fracture. Moreover，ABAQUS software combined with the Gurson-Tvergaard-Needleman (GTN) model for metal ductile-fracture damage was used to numerically analyze the small punch tensile test process. The different parameter values of the improved GTN model were obtained through subsection optimization and the least-squares method. The final simulation results were similar to the experimental results. On the basis of the deformation process analysis of small punch test，the qualitative relationship between the critical void volume fraction and fracture volume fraction and the maximum load and its displacement in GTN model are proposed.

small punch test；finite element；GTN model；load-displacement curve

TG142.25

A

0493-2137(2022)03-0283-08

10.11784/tdxbz202009062

2020-09-23；

2020-12-16.

赵 雷（1985—  ），男，博士，副教授.

赵 雷，zhaolei85@tju.edu.cn.

国家自然科学基金资助项目(52075374)；天津市科技资助项目(20JCQNJC01500).

Supported by the National Natural Science Foundation of China(No.52075374)，Tianjin Science and Technology Project(No.20JCQNJC015 00).

(责任编辑：田 军)