大坝洪水漫顶风险率理论研究

张文灿

（深圳市广汇源环境水务有限公司九江分公司,江西 九江 332000）

1 引言

我国是一个地势特别复杂的国家,由于地势复杂,导致我国常年遭遇到洪水的侵害,尤其是南方地区,大洪水直接损害我国人民群众的生命安全和财产安全,虽然每个河流附近,都有大坝屹立在河流之上,但依然没有办法避免这些问题。基于此现象,针对大坝洪水漫顶风险率进行研究分析,这对我国大坝遇洪水漫顶现象产生时,具有重要指导意义。

鉴于此现象的严重性,我国大量学者对此进行大量的研究分析,也得出了相关理论依据。董华飞等[1]研究大坝洪水漫顶情况下涌浪叠加作用,由此进行模型实验。陈生水等[2]利用混凝土面板上构造成分的破坏机理,提出一种数值计算方法,该方法可以有效模拟混凝土面板上构造成分的破坏过程。胡泽林等[3]提出LHS-MC 与Copula 函数算法公式,分析水电站在加固情况下的洪水漫坝率，并控制不同变量研究其变化对结果的影响。石振明等[4]通过研究坝体结构,分析大坝结构问题引起的事故,进而进行室内模型实验、现场试验和数值模拟研究溃决过程下,大坝水土物质移动规律。黄灵芝等[5]基于模糊数学理论,建立历史失事数学模型,利用模糊数学中隶属函数分析失事程度并进行分析。张修照等[6]介绍我国大坝在洪水漫顶时的溃坝过程,并提供资料分析其中原因。李清富等[7]根据洪水漫顶导致大坝溃坝的原因进行分析,对大坝洪水漫顶风险情况进行评估,并建立风险模型,探讨不确定因素对洪水漫顶风险率的影响以及解决方法。张兴凯等[8]建立物理模型演示尾矿库的大坝在洪水漫顶情况下的溃坝过程。基于冲刷机理和模型相似理论,分析在洪水来临时的防护措施。

由上述研究情况可知,虽然目前对于大坝洪水漫顶风险率研究得到多方学者探究,但没有考虑洪峰、洪量相关关系,也未对比多种计算函数的结果,并进行对比。本文通过数值计算,研究大坝前端最高水位分布情况和系数大小对大坝洪水漫顶风险率的影响。

2 计算模型

2.1 工程概况

某大坝建设工程位于河流下游,且水流湍急,该地区位于我国南方,多雨,因此每有大雨降临之时,便会产生洪水。大坝所处流域面积为14430 km2,选择洪水时间超过7 天的过程。坝高为206 m,高度为151 m,长度为654 m。而大坝的隔河水位线高192.2 m,并且拥有5 亿m3储水库容。利用公式计算,研究大坝在洪水来临时的风险率。

2.2 模型建立

本试验通过风险率理论公式进行计算,建立风险分析模型并对其洪水峰量进行分布处理和风险率计算。基于分析模型的建立,得出风险率的表达式为：

式中：L 为系统荷载；R 为其对应抵抗力。

L 和R 的情况可以反映出工程结构和实际存在的问题。对于分析模型,水库最高水位为Hmax,其也表示大坝能够承受的最大荷载,是抗力,由此得到计算公式：

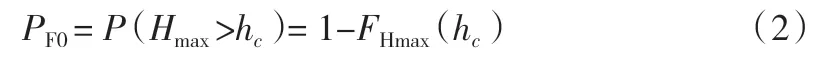
式中：FHmax（hmax）为最高水位Hmax的概率分布情况函数。

由于在实际工况中,FHmax（hmax）难以被求出,由此通过蒙特卡罗模拟法对风险率进行求解。假设Q 和W 分别为洪峰和洪量,其分别对应小写字母q 和w 表示,将Q 和W 进行联合,形成一个二维分布函数：

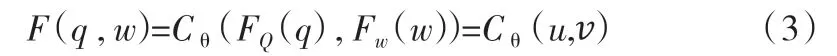
式中：u 和ν 分别为边缘分布情况；F（q,w）为Q,W 的联合分布函数；为公式参数。

利用三种变量公式,分别为Gumbel-Hougaard、Frank 和Clayton,对公式进行依次1～3 的编号编辑,建立公式τ与值的关系表,如表1 所示。并由此计算出统计量Sn,公式如下所示：

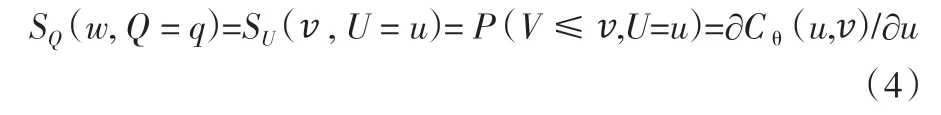
表1 三种编号对应的公式与τ 值的关系表

基于洪水峰量的分布情况,对风险率进行计算,求解洪水漫顶风险率。通过Copula 函数得出洪水的过程线：

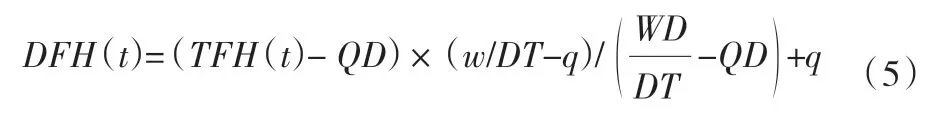
式中：DFH（t）和（TFH（t）分别为洪水过程和在t 时的洪水流量；QD、WD、w 和q 分别为洪峰流量、DT 时间内的洪量、洪峰流量和洪量。

重复Copula 函数计算n 次,可以得到Hmax值,并采用期望公式可得洪水漫顶风险率计算公式：

3 结果分析

3.1 分布情况的确定

根据某城市某项目大坝位置,选择水库洪峰和洪水时间超过7 天的洪水过程进行参数设计,具体情况见表2。

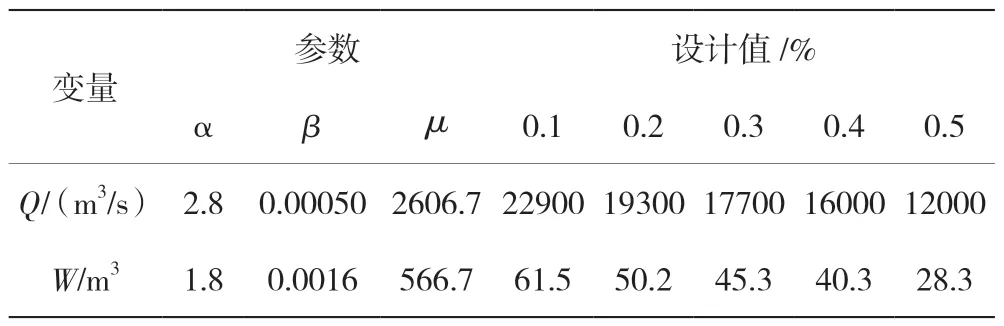
表2 水库参数设计值

将表1 的计算公式与表2 的参数进行结合,建立洪峰和洪水时间超过7 天洪水量的联合分布情况,并且基于Kendall算法计算参数,具体情况见表3。

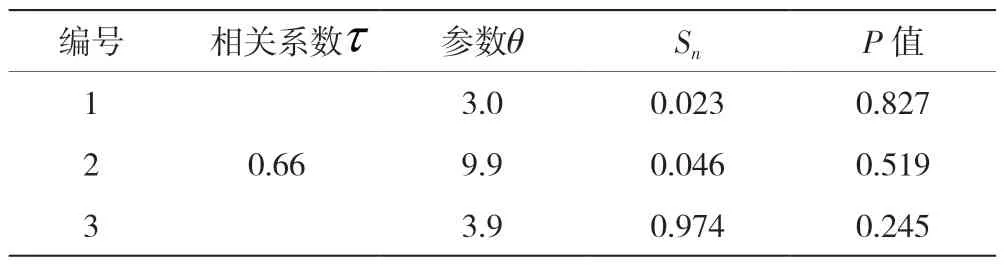
表3 库参数设计值

由表3 可知,P 值均大于0.05,表明设计都是合理的。由此对观测变量的经验分布情况和理论分布情况进行了对比,见图1。

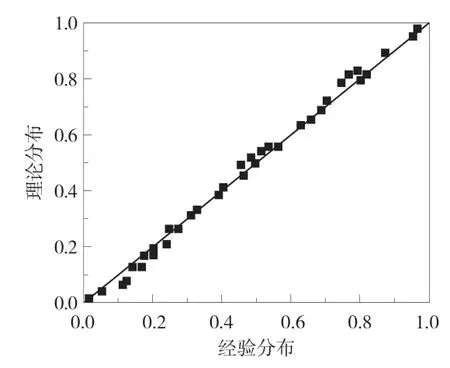
图1 经验分布情况与理论分布情况对比曲线

由图1 可知,对比斜角为45°,表明两种情况的一致性,证明经验频率与理论频率的分布拟合情况很好,建立的分布模型也是合理的。

3.2 计算结果

基于对风险率计算过程,建立计算函数,根据条件分布随机生成大量的洪峰和洪量,并对其进行组合,得出其相关结构。并且根据洪水时间超过7 天洪水量的过程,以经验频率为基础,基于期望公式得出大坝前端的最高水位分布曲线见图2。

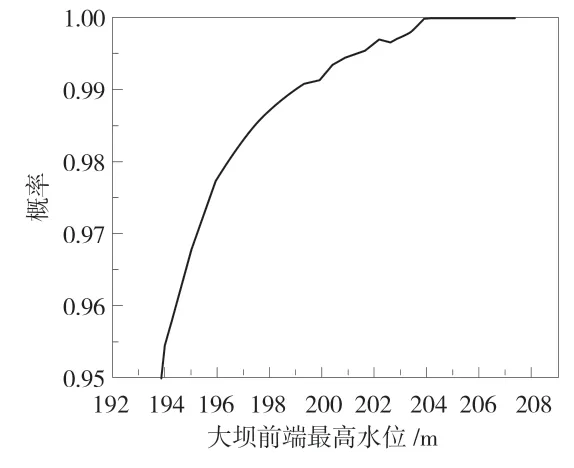
图2 大坝前端的最高水位分布对比曲线

由图2 可知,概率与大坝前端的最高水位曲线分布,在大坝最高水位为204 m 时,概率已经接近1,由此可以得出其风险率为379000。

3.3 取值的影响分析

三种函数对应的大坝前端最高水位分布曲线见图3,其中编号1～3 分别为Gumbel-Hougaard、Frank 和Clayton 函数公式。

图3 三种函数公式对应的大坝前端最高水位分布曲线

由图3 可知,三种概率公式都在大坝前端最高水位204 m 时,概率达到1,其中编号3 算法的概率幅度最大。当大坝前端最高水位为195 m 左右时,编号2 算法的概率幅度超过编号1 算法概率幅度,但当大坝前端最高水位198 m 左右时,编号1 算法和编号2 算法的概率幅度极为接近,并且曲线保持一致的角度。可以肯定编号1 算法和编号3 算法低估洪水风险,编号2 算法高估洪水风险,因此不同编号算法的风险率具有很大差异程度,所以在选择算法时需要仔细斟酌。

3.4 系数大小影响分析

系数大小与大坝前端最高水位概率分布情况情况见图4。

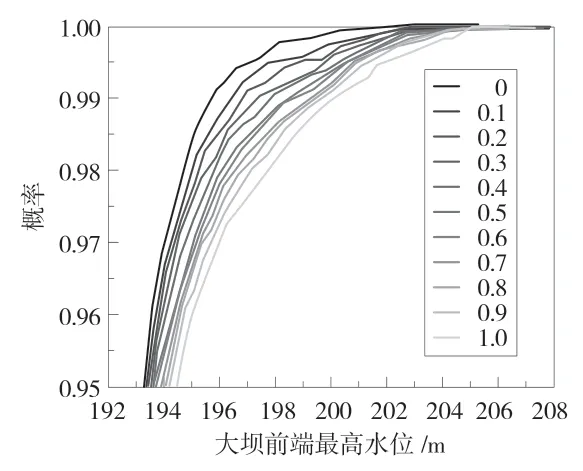
图4 不同系数与大坝前端最高水位概率分布曲线

由图4 可知,随着系数增大,概率随之变小,但当大坝前端最高水位升高时,最终概率都会回到1,其变化曲线幅度会随着系数大小变大而变缓。为进一步研究系数与风险率关系,建立与之对应的洪水漫顶风险率与系数关系曲线,见图5。

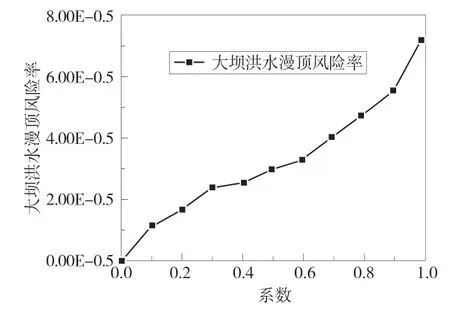
图5 不同系数与洪水漫顶风险率关系曲线

由图5 可知,随着系数的增加,大坝洪水漫顶风险率也随之增加,并且相关系数为0、0.5 和1 所对应的大坝洪水漫顶风险率分别为0、2.9 和 7.2,由此可知,在相关前提条件下,是被高估了,但在不相关情况下则是被低估了。

通过系数大小对漫顶风险率概率分析可知,Copula 函数计算方法合理有效,其能够准确得到洪峰、洪量的相关关系,使公式计算得到大坝洪水漫顶风险率更贴近事实。

4 结论

（1）理论分布情况和经验分布情况对比,表明两种情况一致性,证明经验频率与理论频率分布拟合情况很好,建立分布模型也是合理的。

（2）大坝前端最高水位为204 m 时,概率已经接近1,由此可以得出其风险率为379000。

（3）三种概率公式都在大坝前端最高水位204 m 时,概率达到1,编号3 算法概率幅度最大。当大坝前端最高水位195 m 左右时,编号2 算法超过编号1 算法概率幅度,但当大坝前端最高水位198 m 左右时,编号1 算法和编号2 算法的概率幅度极为接近,并且曲线保持一致的角度。但编号1 算法和编号3 算法低估洪水风险,编号2 算法高估洪水风险,并且不同编号算法风险率差异程度很大。

（4）随着系数的增加,大坝洪水漫顶风险率也随之增加,并且在相关前提条件下,大坝洪水漫顶风险率被高估了,但在不相关情况下则是被低估了。从而得知Copula 函数计算方法合理有效,其能够准确得到相关系数,更加贴近实际应用。