智能客车多目标优化纵向速度跟踪算法设计

李君宝，王洪亮

（南京理工大学 机械工程学院，江苏 南京 210094）

车辆保有量的急剧增大不可避免地带来了交通堵塞、事故频发等问题。智能车辆是智能交通系统的关键环节，可作为减少交通事故、交通堵塞和环境污染的有力手段，因此，吸引了研究者的广泛关注[1]。

纵向控制是智能车辆研究领域中的核心问题之一。许多方法已经被应用于车辆纵向速度控制，其中比例积分微分（Proportion Integration Differentiation, PID）控制是最实用易行的[2-3]。

模型预测控制可以很好地解决多目标和约束的难题，但目前的问题是在单片机上使用时计算量大导致实时性较差。目前，也有很多学者发表过模型预测控制的相关论文。ZHU 等人提出了一种分层控制策略，上层采用模型预测速度控制方法，采用了简化的二次规划（Quadratic Programming, QP）求解算法，减少了解算时间。但提出的方法是否适用于结构差异很大的纯电动无人车有待验证，同时下层控制仅仅采用了逆模型，没有加入控制算法[4]。此外，为了使纵向速度跟踪过程中驱动/制动平顺切换，部分研究者提出了混杂模型预测控制算法[5]。VAFAMAND 等人采用了非线性模型预测控制方法，将电动汽车表示为带偏置项的线性变参数模型，可以很好地跟踪期望电机转速和电流。但影响到乘员舒适性的车辆加速度及其变化率的大小和约束并未详述，同时液压制动系统并未涉及[6]。MAJDOUB 等人使用的车辆非线性模型考虑得很全面，把车辆-地面接触的情况也包括了，但对模型预测控制器（Model Predictive Control, MPC）来说这样的预测模型过于复杂，不利于实车单片机实时性的实现[7]。

本文提出了一种基于模型预测控制与抗积分饱和比例积分（Proportion-Integration, PI）分层控制的智能客车多目标优化速度跟踪算法，以满足智能客车纵向车速的快速跟踪、电池续航能力和乘员舒适性等优化要求。上层控制算法采用模型预测控制，目的是产生期望加速度；下层控制接收上层控制器产生的期望状态值，并根据逆纵向模型产生需求电机转矩与需求制动压力值，再使用抗积分饱和PI控制实现电机转矩和制动压力的反馈矫正，从而实现车辆纵向速度跟踪控制的功能。

1 纵向控制建模

本文的目标车辆为苏州金龙某型智能客车，整车构型如图1所示，动力传动系统包括电机、电池、主减速器，控制系统有纵向控制器、电机控制器、制动系统、电池管理系统。

图1 智能客车整车构型

1.1 车辆纵向动力学分析与建模

驱动过程，车辆纵向受力如图2所示。

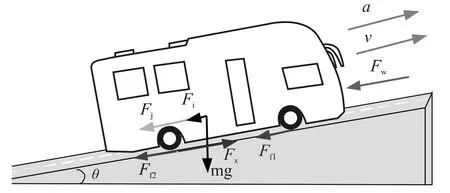
图2 车辆驱动的纵向受力图

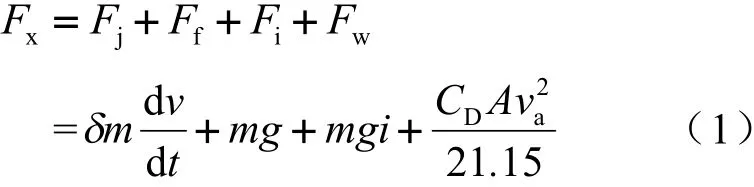
式中，Fj、Ff、Fi、Fw分别为加速阻力、滚动阻力、坡度阻力和空气阻力（N）；Fx为电机系统驱动或制动系统产生的作用于轮胎的地面切向力（N）；δ为旋转质量换算系数；m为汽车总质量（kg）；v为车速（m/s）；f为滚动阻力系数；g为重力加速度（9.81 m/s2）；i为道路坡度；CD为空气阻力系数；A为迎风面积（m2）；va为车速（km/h）。制动过程中，Fj、Fi和Fx的方向和驱动时相反。

1.2 动力电池建模

本文采用的磷酸铁锂电池基本参数如表1所示。

表1 动力电池基本参数

忽略其化学极化作用，以等效内阻模型为基础对动力电池模型进行搭建，等效内阻模型如图3所示。

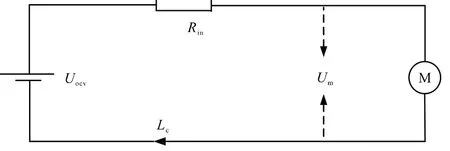
图3 等效内阻模型

根据基尔霍夫电压原理，有

式中，Ic为电池电流（A）；Rin表示电池等效内阻（Ω）；Uocv表示电池开路电压（V）；Um表示电池端电压（V）。

可得电池终端功率：

假设动力电池在电池管理系统的控制下，温度保持为定值，等效内阻不变。电池开路电压Uocv和荷电状态（State-of Charge, SOC）的数据根据实际工程得到，关系如图4所示。

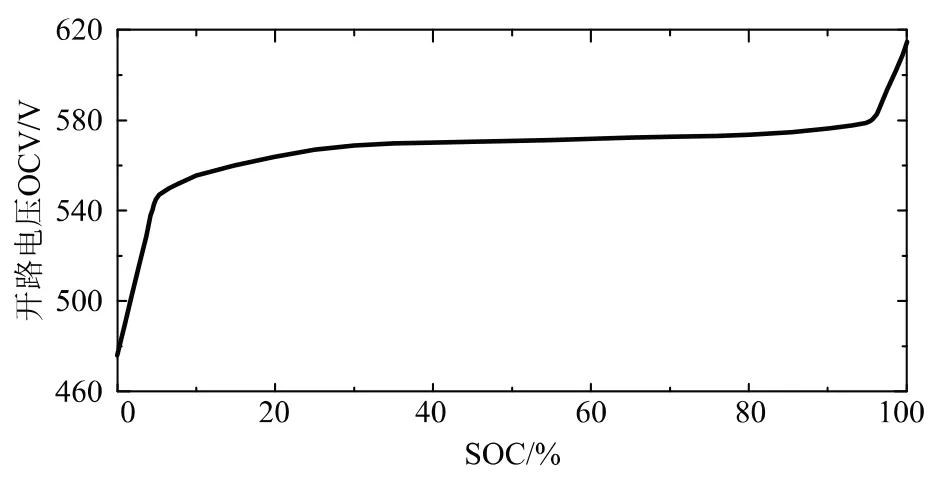
图4 动力电池开路电压OCV与SOC的关系曲线

电池SOC可采用以下公式进行描述：

式中，SOC0为动力电池初始SOC（%）；Qe为电池的额定容量（Ah）；t为放电时间（h）。

回馈入动力电池中的能量，其计算公式如下：

1.3 驱动电机系统建模

本文选择忽略电机的内部动态特性，将研究重点放在电机系统的力矩输入输出特性上。电机系统的结构如图5所示。根据经验公式，电机系统模型可由以下一阶滞后模型表示[8-9]。

图5 电机系统结构图

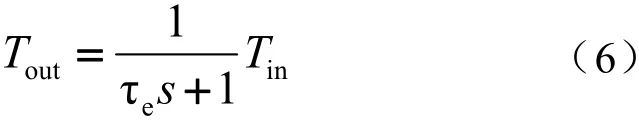
式中，Tout为电机系统输出转矩（Nm）；Tin为电机系统输入转矩（Nm）；τe为时间常数（s）。时间常数的取值非常关键，必须使转矩输入-输出曲线和实际电机测量曲线相匹配，可在仿真环境下通过反复试验选取[10-11]。当τe=0.015时，电机系统响应贴合真实试验曲线。

电机的外特性曲线（图6）和效率MAP图（图7）可通过实验台架获取。驱动电机基本参数如表2所示。

图7 电机系统效率MAP图

表2 驱动电机基本参数

图6 电机额定外特性曲线

驱动电机功率的计算公式为

式中，Pe为驱动电机功率（kW）；I为电机电流（A）；U为电机电压（V）；ω为驱动电机角速度（rad/s）；n为驱动电机转速（r/min）。

1.4 制动系统执行器建模

采用理论分析方法建立制动系统执行器模型相当复杂，为了简化过程，把制动系统执行器建模视为灰箱式辨识问题，采用系统辨识来确定执行器的数学模型[12-13]。

首先，通过实验台架得到制动系统的需求轮缸制动压力Pb,des的输入值序列{uP(k)}和液压传感器得到的实际轮缸制动压力Pb,act的输出值序列{yP(k)}。然后，利用 MATLAB 的系统辨识工具箱可得到包括液压驱动单元和液压控制单元在内的制动系统模型。

2 基于模型预测控制的上层控制算法设计

模型预测控制可以同时处理多个目标，如速度跟踪精度、乘员舒适性和燃油经济性等，同时也可以处理现实电机系统和制动系统中存在的约束条件。

2.1 预测模型

在车辆的横摆运动的幅度较小的情况下，可以近似地认为车辆的纵向加速度等于纵向速度的一阶导数：

又考虑到车辆下位控制系统存在响应时滞，所以可以利用一阶惯性环节来近似的表示智能客车的纵向运动特性[9,14]：

式中，K=1.0为系统增益；τ=0.5为时间常数。

考虑速度与加速度的关系，连续系统状态空间方程表示如下：

对上述状态空间方程进行离散化，这里用前向差分法实现，得到的离散系统的状态空间方程如下：

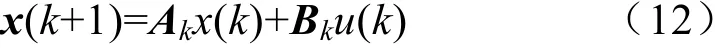
纵向速度控制目标是对参考速度的精准跟踪，所以输出量为纵向速度v，输出方程可以写成如下的形式：y(k)=Ckx(k) （13）

式中，Ck=[1,0]。

为了将上述离散系统状态空间方程转化为便于计算机求解的QP问题，可做如下变换：

可得到新的状态空间表达式：

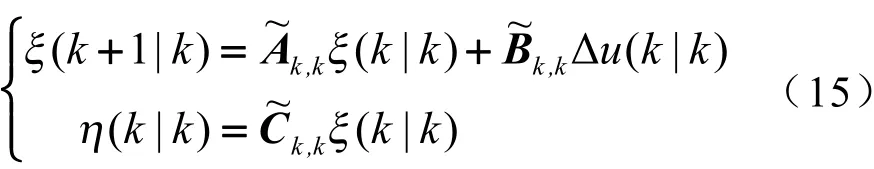
在预测时域内，状态变量和输出变量都可以通过系统当前的状态变量ξ(k|k)和控制时域内的控制增量Δu(k)推断得到，这体现了模型预测控制算法中的“预测”功能。

2.2 优化求解

因为此时系统的控制增量是未知的，所以得设定合适的优化目标和约束条件，并将优化问题转换为二次规划问题进行求解，才能得到控制时域内的控制序列。本文选取了纵向速度跟踪精度、乘员舒适性和燃油经济性三个性能指标作为模型预测控制算法的优化目标，通过调节各个指标的权重系数，实现多目标问题的协调优化。给出的代价函数如下：

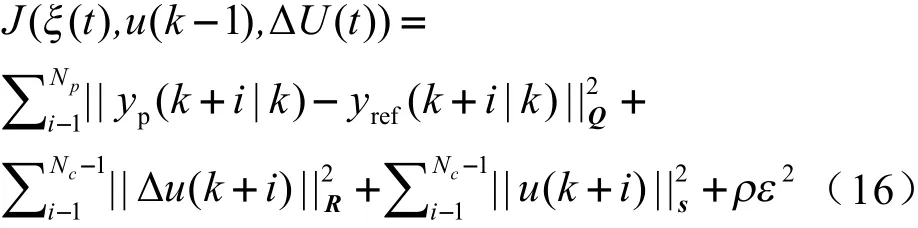
式中，Np为预测步长；Nc为控制步长；yp(k+i│k)为控制输出预测值；yref(k+i│k)为控制输出参考值；(k+i│k)表示根据k采样时刻的信息来预测k+i时刻的值，其中i=1,2,…,Hp；u(k+i)和Δu(k+i)分别是k+i时刻的系统控制输入和控制输入增量，其中i=0,1,…,Hc-1；Q、R、S分别是系统输出变量、控制增量和控制量的权重矩阵；ρ为松弛因子的权重系数；ε为松弛因子。

在式（16）中，第一项代表了系统对参考速度的跟随能力，第二项、第三项分别代表对控制量及其变化率的约束。

本文对加速度和加速度变化率进行了硬约束，以使乘员感觉处于舒适范围内，约束如下：

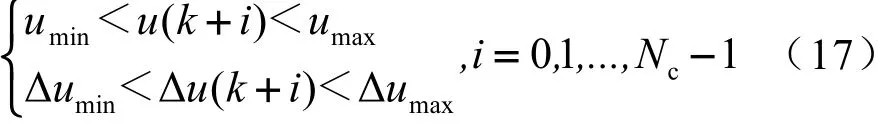
2.3 反馈矫正

通过二次规划问题的求解，就可以得到控制增量ΔU(k)=[Δu(k),Δu(k+1),…,Δu(k+Nc)]T，将控制增量序列中的第一项取出，通过公式u(k)=u(k-1)+Δu(k)就能够计算出当前时刻的控制量。在下一控制周期，利用车载传感器再次获取车辆的运动状态并重复优化求解过程，便可以不断地修正当前车速，实现车辆纵向速度控制系统的闭环控制。

至此，MPC设计完成，其关键参数如表3所示。

表3 MPC控制器关键参数

3 基于抗积分饱和PI控制的下层控制算法设计

3.1 智能客车逆纵向动力学模型

3.1.1 驱动系统逆模型

驱动系统逆模型是指从驱动轮转矩到驱动电机需求转矩的传递关系。分析可得驱动轮转矩为

式中，Tt为驱动轮转矩（N）；Tm为驱动电机需求转矩（Nm）；i0为主减速器传动比；ηT为传动系的机械效率（%）。

由式（1）可得驱动电机需求转矩为

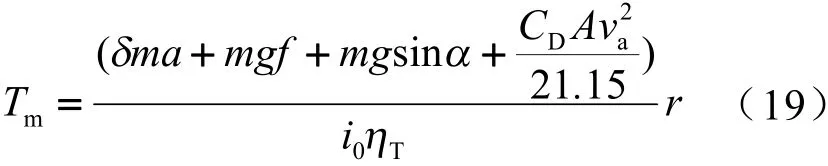
此外，需要根据驱动电机的外特性对驱动电机需求转矩进行限制。驱动电机系统的输入转矩由下式决定：

式中，Tmmax为当前状态下电机可输出的最大转矩（N·m）。

肝癌为临床常见恶性肿瘤,发病隐匿,多数患者出现临床症状时已为晚期,5年存活率<10%。因此,肝癌早期诊断具有重要意义,甲胎蛋白(AFP)为临床诊断肝癌的常见血清肿瘤标记物,但其敏感性约39%~64%,特异性约为76%~91%,易出现误诊、漏诊情况,给临床诊断和治疗带来不便[1]。研究指出[2],肝癌组织因各因素导致PIVKA-II释放入血,但其作用机制尚未完全明确。

3.1.2 制动系统逆模型

制动系统逆模型是指从车轮制动力到期望制动轮缸压力的传递关系，建模过程如下。

首先，根据上层控制算法输出的期望加速度计算出期望制动力矩。由式（1）可得到期望制动力矩为

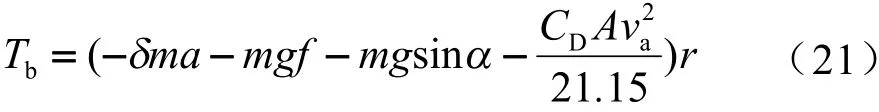
然后，通过制动能量回收控制策略对期望制动力矩进行分配，计算出液压制动系统的需要承担的制动力矩。

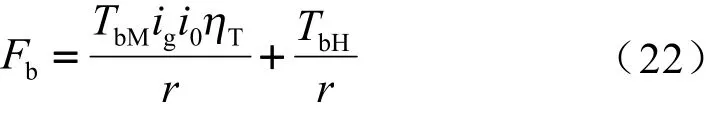
式中，TbM、TbH分别是制动力分配后电机系统、制动系统所承担的制动力矩。

最后，由期望制动压力得到期望制动轮缸压力。如图8所示，对制动车轮受力分析得

图8 制动轮受力图

式中，Iω为车轮转动惯量（kg·r2）；ω为车轮转动角速度（rad/s）；Tμ为制动器的摩擦力矩（Nm）。因为Iω较小，所以忽略其对制动过程的影响。

根据液压传动知识，并忽略压力传递过程中的液压损失，可求得制动器摩擦力矩（单个轮缸）的表达式为式中，p为制动轮缸压力（Pa）；d为轮缸直径（m）；rb为制动鼓半径（m）；Kef为制动效能因数。

联合式（23）、式（24）可得制动轮缸压力与地面制动力的关系（单个轮缸）：

3.2 制动/驱动切换逻辑

在车辆正常行驶过程中加速和制动是不能同时存在的。在需要制动时，应先借助滚动阻力、空气阻力来降低车辆行驶速度，若需要更大的减速度再利用电机或液压制动系统来获得更大的制动力。此外，为了提高乘员舒适性和执行器的使用寿命，不能频繁切换制动/驱动的控制状态。为了解决以上问题，设置了驱动/制动缓冲带[15-16]。

车辆空挡滑行时的临界减速度如下：

将任意车速下的a0计算出来，可以绘制一条v-a0的曲线。在该曲线的基础上平移Δh得到一条缓冲带。根据经验，一般取Δh=0.1 m/s。驱动/制动切换逻辑如图9所示。

图9 制动/驱动切换逻辑

3.3 基于抗积分饱和PI控制的执行系统控制

为避免控制量长时间停留在饱和区，引入了抗积分饱和PI算法。该方法的思路是在计算控制器输出变量u1(k)时，首先判断上一时刻的控制量u1,2(k-1)是否已经超出了限制范围。若u1,2(k+1)＞u1,2max，则只累加负偏差；若u1,2(k+1)＜u1,2min，则只累加正偏差。所设计的电机控制系统和制动器控制系统结构如图10所示。

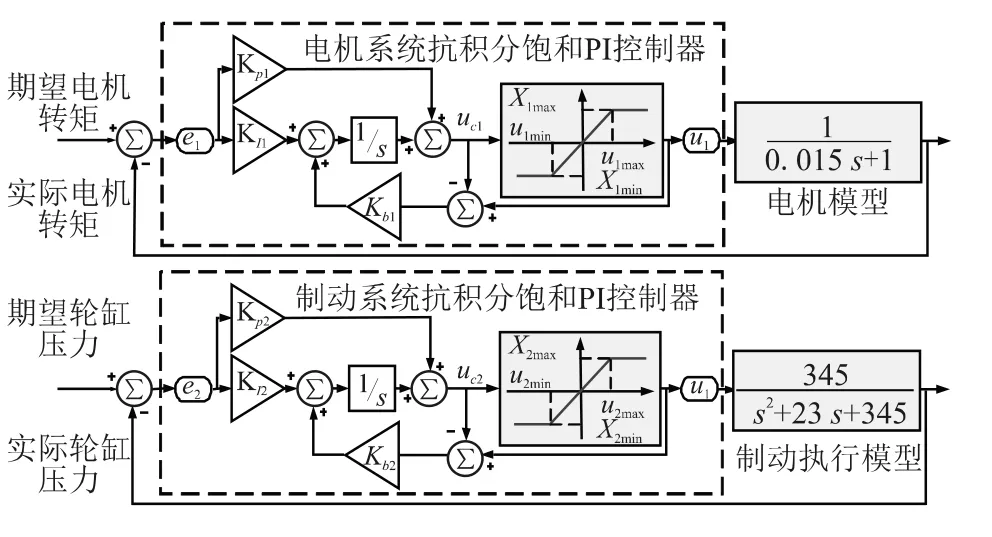
图10 电机控制系统和制动器控制系统

图中，KP1、KP2为比例系数；KI1、KI2为积分系数；u1max、u1min分别为电机输出扭矩的最大值、最小值；u2max、u2min分别为制动轮缸压力的最大值、最小值；Kb1、Kb2为反算系数，其绝对值越大，控制器退出饱和状态的能力越强，但过大的值也会造成超调，所以取值要合理。抗积分饱和PI控制器参数如表4所示。

表4 抗积分饱和PI控制器参数

4 仿真结果与分析

联合仿真模型如图11所示。仿真道路为平直混凝土路，附着系数为0.85。智能客车的仿真参数如表5所示。为了验证提出的算法是有效的，本文将从控制算法鲁棒性、速度跟踪精度、乘坐舒适性和电池续航能力四个方面进行了对比。

表5 智能客车关键参数

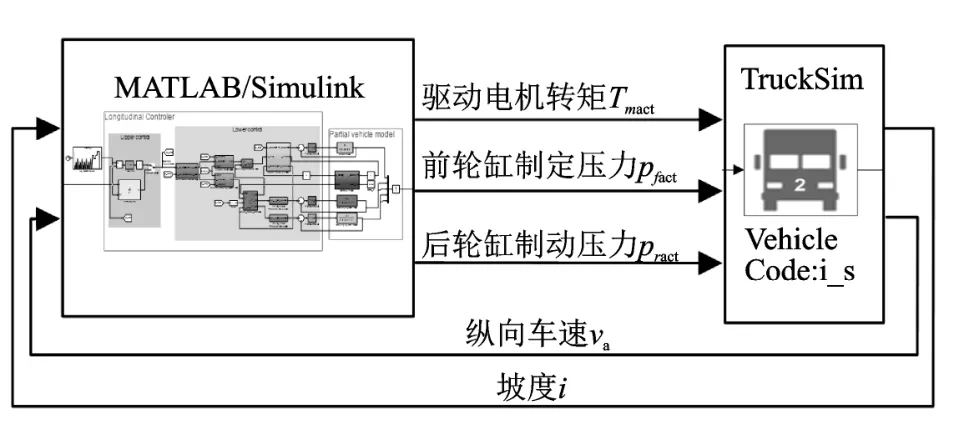
图11 MATLAB/Simulink-Trucksim联合仿真模型

4.1 控制算法鲁棒性

为了研究所提控制算法对外界干扰的鲁棒性，本文进行了不同道路坡度下的速度跟踪仿真。三次仿真的道路坡度i的绝对值|i|分别设为4%、6%、8%，每次仿真试验包含一个上坡和一个下坡。

从图12可以看到，智能客车在不同道路坡度路段交接处，由于驱动电机和制动系统的非线性和时滞性，实际车速曲线会产生一定的振荡和超调，但在所提算法的调节下，车速很快便会趋于稳定。为了进一步对比，截取了图13中22～60 s的曲线（期望速度为40 km/h），计算了不同道路坡度下速度的最大误差Emax、平均绝对误差（Mean Absolute Error, MAE）和均方根误差（Root Mean Square Error, RMSE），如表6所示。

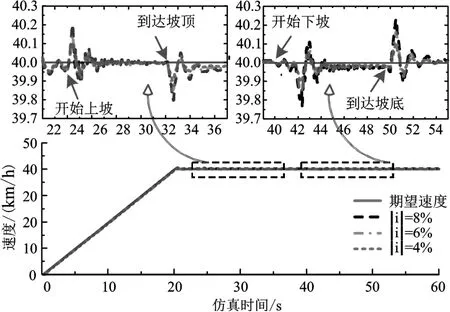
图12 不同道路坡度下的速度跟踪

图13 不同道路坡度下的速度偏差

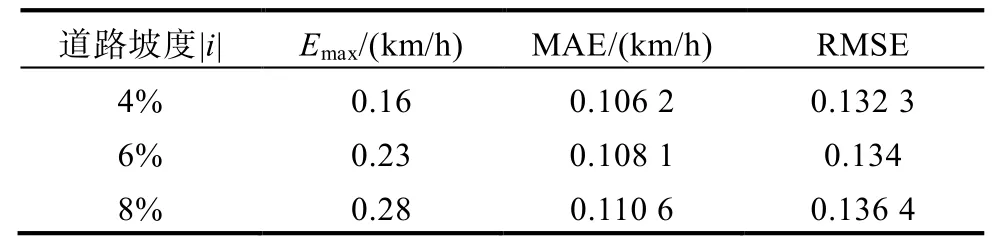
表6 不同道路坡度下的速度误差

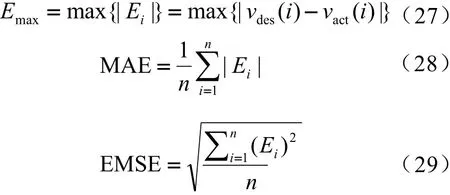
其中，式中，vdes(i)、vact(i)分别为期望速度、实际车速的第i个采样值，km/h；i=1,2,…,n；n为采集的样本数据个数。最大误差Emax代表的是局部误差，其值越小表明控制精度越好。绝对平均误差MAE代表全局误差。均方根误差EMSE用来衡量误差的离散程度，其值越小，控制稳定性越好。

在坡度 8% 的道路上，坡道干扰是最大的，但速度最大误差也仅为0.28 km/h，相当于参考速度的0.7%。同样，8%坡度工况的均方根误差为0.136 4，也就是说，在误差统计发布是正态分布的情况下，随机速度偏差落在±0.136 4以内的概率为68%。从以上分析可得，所提算法对外界干扰具有较好的鲁棒性。

4.2 速度跟踪精度

速度跟踪精度是评价纵向运动最重要的指标，它直接影响车辆安全。为了更精确地评价速度跟踪精度，本文在欧洲续航测试标准工况（New European Driving Cycle, NEDC）下，从最大误差Emax、平均绝对误差MAE 和均方根误差RMSE三个方面，进行了对比与验证。如图14所示。

低速时，由图14(b)可以看出，MPC+PI控制器可以对期望速度做出快速的响应，跟踪误差可以维持在0.5 km/h以内，而PI+PI控制器会有一定的超调和振荡，加、减速跟踪过程中会存在大于1 km/h的静态误差。高速时，车辆存在高非线性和复杂约束。由于PI+PI控制器的参数是不变的，只适用于特定场景，所以控制效果会变差。由图14(c)可以看出，即使期望速度不变，PI+PI控制也会比MPC+PI控制存在更大的静态误差。因此，MPC+PI控制可以很好地处理非线性带来的速度跟踪误差。

图14 不同算法的速度跟踪仿真结果对比

为了对比更清晰，对速度跟踪误差进行了处理，计算结果如表7所示。MPC+PI的最大速度误差Emax为1.53 km/h，小于PI+PI的2.76 km/h，说明MPC+PI的速度局部精度更高，相比PI+PI提高了44.6%。MPC+PI和PI+PI的MAE分别为0.24 km/h、0.6 km/h。相比PI+PI，MPC+PI的速度全局精度提高了60%。MPC+PI的速度均方根误差RMSE为0.15，相比PI+PI，提高了64%。由此可见，所提MPC+PI控制算法可以有效提高速度控制误差的稳定性。

表7 不同算法的速度误差

4.3 乘员舒适性

平顺性是现代高速车辆的主要性能之一，代表了乘员主观感觉的舒适性。根据ISO 2631—1:1997(E)标准规定，可以用加权加速度均方根值aw来评价振动对人体舒适性的影响。本文采用频谱分析法，对加速度a(t)进行频谱分析得到功率谱密度函数Ga(f)，从而得到加权加速度均方根值为

式中，w(f)为频率加权函数；f为频率（Hz）。w(f)由以下公式得到：

如图15(a)所示，因为对加速度进行了限制，所以MPC+PI和PI+PI的加速度均在[-1.5,1]范围内。从图15 (b)可以看出，MPC+PI的加速度控制比PI要快速和平稳。PI+PI控制的加速度会存在滞后、超调和振荡，这也导致了车辆在驱动和制动之间的切换更加频繁，如图15 (c)所示，从而使得车辆平顺性变差。振荡现象的存在，直接导致了高频率加速度的产生。从图15 (d)可以看到，低频时（0.5～20 Hz）MPC+PI和PI+PI的加速度功率谱密度非常接近，高频时（20～80 Hz）PI的加速度功率谱密度比MPC高，所以PI+PI的加权加速度均方根值会更大。

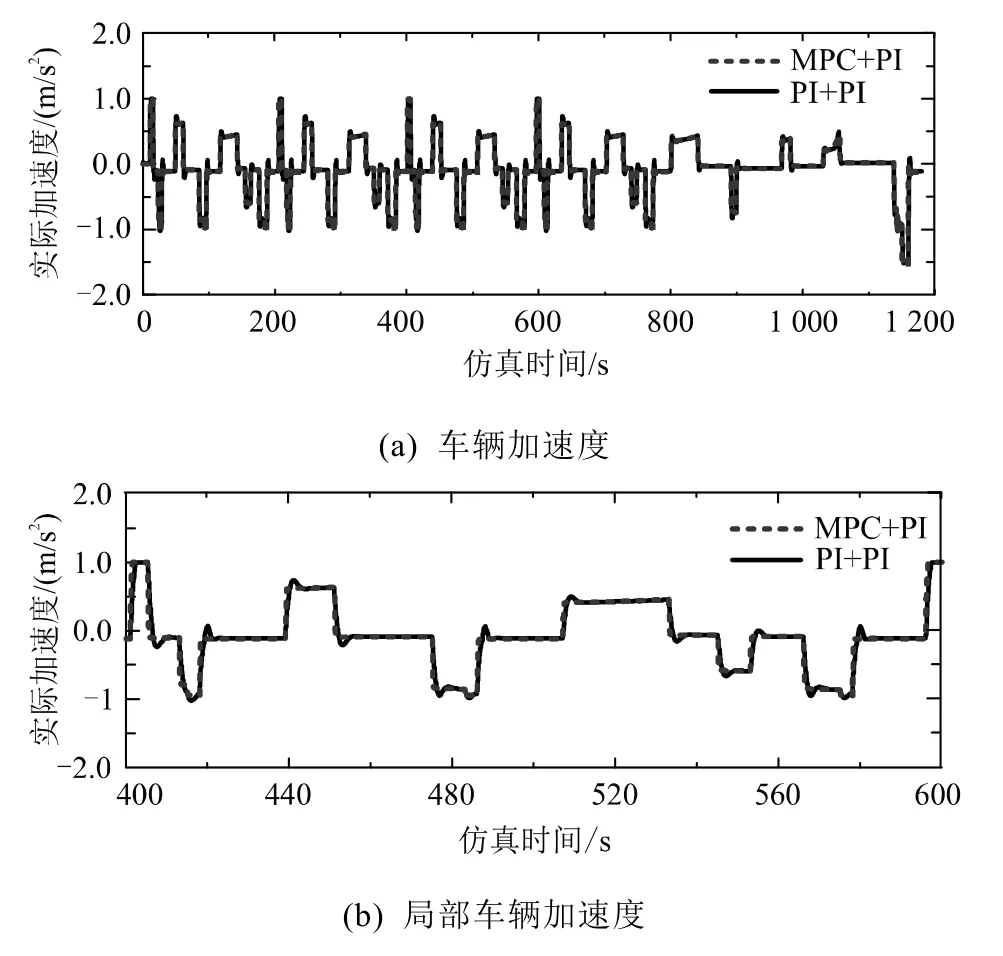
图15 NEDC工况下不同算法的车辆加速度仿真结果

从表8的数据统计结果来看，NEDC工况下PI+PI和 MPC +PI的加权加速度均方根值分别为0.223 m/s2、0.199 m/s2，均没有超过0.315 m/s2，处于保持乘员舒适性的范围之内，这是因为对加速度进行了限制且只考虑了车辆的纵向加速度。实际情况会更复杂，还得考虑路面和车辆侧向加速度的影响。总的来看，MPC+PI的平顺性要好于PI+PI，性能相比PI+PI提升了10.76%。

表8 NEDC工况下不同算法的加权加速度均方根值

4.4 电池续航性能

因为NEDC工况下不同算法的车辆行驶里程变化不大，所以本文使用电池SOC来评价电池续航性能。再生制动能量回收功能开启的情况下，PI+PI和MPC+PI的SOC使用量分别为3.1%、3.0%，说明相同行驶里程下MPC+PI的续航性能更强，相比PI+PI提升了3.2%。再生制动能量回收功能关闭的情况下，PI+PI和MPC+PI的SOC使用量分别为4.2%、4.0%，说明相同行驶里程下MPC+PI的续航性能相比PI+PI提升了4.7%（见表9）。所以不管制动能量回收功能是否开启，MPC+PI的续航性能都得到了有效提升。此外，制动能量回收功能开启下的SOC使用量远小于无再生情况下的SOC使用量，见图16(a)。

表9 NEDC工况下不同算法的SOC使用

综上所述，电池的续航能力主要是由所提的制动能量回收策略决定的，其次受纵向速度跟踪算法的影响。相比PI+PI控制，MPC+PI控制下的电池电流变化会更加平稳，振荡现象不明显，见图16(b)，所以电池充电也更稳定，效率更高。

图16 NEDC工况下不同算法的续航能力

5 结论

本文提出了一种基于改进MPC和抗积分饱和PI分层控制的智能客车纵向速度跟踪控制算法。该算法同时考虑了电池续航性能和乘员舒适性，以满足智能客车的多目标优化要求。首先，上层控制采用了改进的MPC方法，可以实时产生理想的平滑加速度。然后，下层控制采用抗积分饱和PI实现对电机扭矩和轮缸制动压力的反馈矫正。最后，进行了MATLAB/Simulink-Trucksim联合仿真验证。

仿真和试验验证结果表明，提出的改进MPC加抗积分饱和PI控制算法比PI加抗积分饱和PI方法具有更高的速度控制精度，具有更快的响应和更小的超调量。所提算法可以有效处理纵向跟踪过程中车辆的非线性和不确定性干扰，其良好的跟踪性能减少了驱动/制动切换次数，提升了乘员舒适性，延长了执行机构的使用寿命。此外，进入能量再生模式时所提方法可以产生平稳的回馈电流，电池充电效率更高，电池续航性能也可以得到有效提高。

进一步的研究仍然有必要。之后，我们将开展纵向和横向的协调控制，测试工况更加复杂，考虑的干扰因素也更多。