基于加权信息量方法的汕头市地质灾害易发性评价

2022-11-29吴勇庆

地下水 2022年6期

吴勇庆

(广东省地质局第二地质大队，广东汕头 515021)

0 前言

地质灾害易发性是指在一定的地质环境条件和人类工程活动影响条件下，地质灾害发生的可能性的难易程度，也被称为地质灾害空间预测、地质灾害敏感性等。地质灾害易发性分区是根据地质灾害形成发育的背景，并结合地质灾害发育现状调查预测评价结果，以定性、定量评价相结合予以确定，目的是阐明区域地质灾害的分布规律，发育特征及危害，为地质灾害防治提供科学基础。

我国是一个地质灾害频发的国家，地震、滑坡、山崩、洪涝、泥石流等地质灾害给中国人民带来了不可估算的损失，制约着国民经济的发展。地质灾害对人类的生活带来了严重的威胁，它可以中断交通线、阻塞河道、掩埋村庄等，破坏性很强[1]。

因为地质灾害的破坏性极大，地质灾害的预测成为了研究热点。地质灾害易发性评价的理论基础是工程地质类比法，纵观其发展历程，经历了从定性—半定量—定量的过程[2]。定量方法是在进行定性分析的基础上，建立预测对象的地质模型，通过合理假设或简化，将复杂的研究对象抽象成可以求解的数学模型，进而选取合理参数，进行预测计算，获得评价预测结果[2]。

信息量模型是地质灾害易发性评价模型中应用得最为广泛的数学模型之一，最早由赵鹏大等人从前苏联引入中国并应用于地质找矿[3]，后来，晏同珍、殷坤龙等将其应用于滑坡空间预测[4-5]。信息量模型理论比较成熟，它能与GIS技术很好的结合，逐渐成为了地质灾害易发性评价的一种有效方法。

在国内，信息量模型在滑坡预测中得到广泛应用，信息量模型理论已经非常成熟，早在1985年，晏同珍、殷坤龙等曾先后多次在陕南及长江三峡库区探索了信息量方法在区域性滑坡灾害空间预测分区中的应用，并与其他方法的研究成果进行了比较性研究。近年来，国内学者利用信息量模型做了大量滑坡空间预测工作[6-18]，例如：2003年，张桂荣，殷坤龙，刘传正等运用信息量模型对陕西省旬阳地区斜坡稳定性进行了空间定量预测。2004年，朱良峰、吴信才、殷坤龙等采用信息量模型对中国范围内的滑坡灾害进行危险性分析和区域社会经济易损性分析，并在此基础上进行最终的滑坡灾害风险评估。2005年，石菊松、张永双、董诚等采用基于GIS技术的信息量模型和敏感性评价方法，实现了巴东县新城区滑坡灾害危险性区划。2006年，高克昌、崔鹏，赵纯勇等结合GIS技术和信息量模型对重庆万州滑坡灾害进行了危险性评价。2009年，孟令超、卢晓仓、史晨晓等利用信息量模型对达曲库区进行了滑坡危险性分析。2010年，卢晓仓，陈泰霖利用信息量模型对某工程库区进行了危险性分析。2011年，牛全福，程维明，兰恒星等基于信息量模型对玉树地震次生地质灾害进行了危险性评价。2011年，赵衡，宋二祥对信息量模型进行了改进和应用，建议引入因素分析评估和减少各因素间的相关性。

当前学者所应用的信息量模型为简化的信息量模型，通过计算单因素信息量，在综合叠加分析，很少考虑因素之间的权重关系，这可能对预测精度产生影响，本文中称这种简化的信息量模型为“理想信息量模型”。如果不单单计算各种因素组合对滑坡灾害提供的信息量，而且，对于区域地质灾害要素综合研究“最佳权重组合”，而不是将各个地质灾害因素设置为等权重，即为“加权信息量模型”。因此，本文以汕头市为研究区，结合GIS技术和加权信息量模型，探讨了研究区地质灾害易发性的分布规律。

1 研究区概况

本文选定的研究区为广东整个汕头市行政区域，辖6区1县，分别为金平区、龙湖区、濠江区、澄海区、潮阳区、潮南区、南澳县，总面积为2 164.64 km2；地理坐标为：东经116°14′26″～117°09′24″，北纬23°02′30″～23°38′54″。汕头市位于广东省东部，濒临南海，位于韩江三角洲南端，北接潮州，西邻揭阳，东南濒临南海，与台湾隔海相望，境内有韩江、榕江、练江三江入海，是中国大陆唯一拥有内海湾的城市，大陆海岸线长217.7 km，海岛岸线长167.37 km，有大小岛屿82个。汕头市全区总面积为2 164.64 km2，其中中心城区面积为419.71 km2，澄海区面积为372.77 km2，潮南区面积为593.80 km2，潮阳区面积为666.63 km2，南澳县主岛面积为111.73 km2。

汕头市地处广东省东部，濒临南海，属于南亚热带季风气候，受海洋性东南亚季风影响很大，且处于低纬度地区，太阳辐射强，日照天数多，平均气温高，夏季盛吹东南风，冬季为北风和偏北风。四季主要特点：春季阴雨天气较多，夏季高温湿热，水汽含量大，常带来大雨、暴雨，秋季常有雷雨、台风雨，冬季寒冷，雨量稀少，霜冻期很短。

汕头市地处海滨冲积平原之上，处在粤东的莲花山脉到南海之间，境内地势自西北向东南倾斜，整个地形自西北向东南依次是中低山—丘陵，台地或阶地—冲积平原或海积平原—海岸前沿的砂陇和海蚀崖—岛屿。东北部有莲花山脉，西北是桑浦山，西南有大南山。东南部沿海沿江出口处为冲积平原或海积平原和海蚀地貌以及港湾和岛屿的分布。韩江、榕江、练江的中、下游流经市境，三江出口处成冲积平原，是粤东最大的平原。

根据区域地质资料，汕头市出露地层为第四系，白垩系、侏罗系和三叠系。其中第四系为全新统、上更新统，白垩系为南山村组(K1n)，侏罗系包括上龙水组(J3sh)、热水洞组-水底山组并层(J2-3r-sd)、银瓶山组(T3J1y)，蓝塘群(T3J1L)，三叠系为小坪组(T3x)。

汕头市区在地貌单元上以河口冲洪积平原为主，其次为沿海丘陵地带。冲洪积平原分布区地表发育了几十米至厚度逾百米的第四系松散堆积层，其中的砂性土层分布连续性好、厚度较大，而且本地区降雨量丰富，为汕头市区地下水的形成、储存、运动提供了优越的水文地质条件。根据工作区内地下水赋存条件，含水层水理性质和水力特征，本区地下水划分类型为松散岩类孔隙水和基岩裂隙水。除此之外，基岩风化壳中发育有网状裂隙水，多赋存于第四系覆盖区。

2 研究方法

2.1 数据来源

2.2 地质灾害加权信息量模型

当不考虑各影响因素的权重差别时，地质灾害(Y)发生的不确定性是与Y的先验概率成反比的，即对Y的不确定性可表示为先验概率的倒数的某一函数。我们取这一函数为以2为底的对数函数，单位为比特(bit)，并把这样定义的不确定性称为地质灾害(Y)的自信息量：

(1)

I(Y)代表两种含义：(1)当地质灾害发生以前，表示地质灾害发生的不确定性；(2)当地质灾害发生以后表示地质灾害所含有的信息量。

当考虑各个因素的影响时，我们把条件概率称为后验概率P(Y∣x1x2…xn)，它是在各因素共同作用下而发生地质灾害的概率。那么，各因素影响下，是否地质灾害尚存在的不确定性应该是后验概率倒数的函数。于是，已经消除的不确定性为：先验的不确定性减去尚存的不确定性。这就是收信者获得的信息量，定义为互信息量：

(2)

式(2)就是信息量的表达式。根据条件概率运算，式(2)可进一步写成：

I(Y；x1x2…xn)=I(Y；x1)+Ix1I(Y；x2)+…+Ix1x2…xn-1(Y；xn)

(3)

式中：I(Y；x1x2…xn)表示因素组合x1x2…xn对地质灾害所提供的信息量(bit)；P(Y∣x1x2…xn)表示组合条件下地质灾害发生的概率；P(Y)表示地质灾害灾害发生的概率；

Ix1I(Y；x2)表示因素x1存在时，因素x2对地质灾害灾害提供的信息量(bit)。

式(3)中，x1x2…xn地质灾害因素组合对地质灾害灾害所提供的信息量等于因素x1提供的信息量，地质灾害加上因素x1确定后因素x2对地质灾害灾害提供的信息量，直至因素x1x2…xn-1确定后，xn对地质灾害提供的信息量。如果采用面积比来计算信息量，对于栅格图层，面积可用栅格单元数近似表示，式(3)则可表示为：

(4)

式中：S表示研究区的栅格单元总数；S0表示研究区内有x1x2…xn的栅格单元数；N表示地质灾害区的栅格单元总数；N0表示地质灾害区x1x2…xn组合的单元数。

由于导致地质灾害灾害的因素很多，相对应的因素组合也就十分多，样本统计数量往往受到限制，故一般采用简化的单因素信息量模型(“理想信息量模型”)分步计算每个地质灾害因素的信息量，单因素xi的信息量公式为：

(5)

理想信息量模型式需要对各个因素的信息量综合叠加，简单的认为各因素之间是等权重的，将式(3)简化为：

(6)

所以得到理想信息量模型的公式为：

(7)

式中：I(Y；xi)地质灾害—地质灾害单因素xi对地质灾害灾害所提供的信息量(bit)；I(Y；x1x2…xn)地质灾害—地质灾害研究区某单元信息量预测综合值(bit)；S表示研究区的栅格单元总数；Si表示研究区含有因素xi的单元总数；N表示地质灾害区的栅格单元总数；Ni表示地质灾害区含有因素xi的单元总数。

通过栅格计算，可以得到每个栅格单元的总信息量值I，其值越大，则表明该单元所在区域发生地质灾害灾害的概率越大。

地质灾害的形成受多种因素影响，信息量模型反映了一定地质环境下最易致灾因素及地质灾害其细分区间的组合；具体是通过特定评价单元内某种因素作用下地质灾害发生频率与区域地质灾害地质灾害发生频率相比较实现的。但该统计分析只是反映了各影响因子在特定组合类别地质灾害情况下灾害发生的概率，未充分考虑各因子对地质灾害发生贡献的差异性。因此，本次采用地质灾害层次分析法(AHP)加权的信息量评价模型，利用层次分析法赋予每个评价因子不同的权地质灾害重，最后进行叠加，使结果更加准确合理。

表1 易发性评价因子选取分级表

3 研究内容及结果

3.1 评价因子选取

基于加权信息模型的计算方式及评价因子的建立原则，结合野外实地调查并对调查范围地质灾害影响因素进行分析，本次共选择6个评价因子建立地质灾害易发性评价因子体系，6个评价因子分别为坡度、坡向、地形起伏度、工程地质岩组、距构造距离和距道路距离，见表1。

3.2 单元格网划分

地质灾害发育的严重程度受到诸多因素的作用，在局部区域又表现出明显的差异性和复杂性，因此，在对研究区进行易发性评价时首先考虑确定的就是评价单元的选取是评价体系建立的基础。目前，国内外研究学者对评价单元的区划方法概括起来大致有几类：规则栅格单元、自然斜坡或地貌单元、行政单元等。本次汕头市地质灾害易发性评价选取规则栅格单元评价单元。依据经验公式来确定所分栅格的大小，将栅格大小确定为10 m×10 m，采用栅格单元表达易发性评价结果，通过对栅格评价结果的分析，划分易发性分区。

3.3 评价因子权重确定及信息量权值计算

根据层次分析法为每个评价因子赋权重值，参考本单位专家意见及野外调查结果，对各因子之间的相互重要性进行打分，构建各因子判断矩阵。

表2 易发性评价因子体系权重层次分析法计算矩阵

采用方根法求出上述判断矩阵的最大特征根λmax=6.227。根据一致性检验可得：CI=0.045，RI=1.260，CR=CI/RI=0.036<0.1，符合一致性，对其相应的特征向量归一化处理，并结合研究区实际情况做出轻微调整，得到各评价因子权重分配(表3)。

表3 易发性评价因子权重分配表

通过使用ArcGIS软件的分析功能，将每个评价因子按照分级要求进行重分类，并分别求得其不同类别的面积，然后将地质灾害点及孕灾地质条件点的空间分布与评价因子的不同级别进行叠加，分析每个级别中拥有的地质灾害点及孕灾地质条件点个数，得到相交后的计算结果，代入单一评价因子的信息量计算公式，求得不同评价因素各个层级对地质灾害所产生的或所提供的信息量以及汕头市地质灾害各评价因子分级图(见图1～图7)。

图1 地质灾害易发性评价因子信息量图(坡度)

图2 地质灾害易发性评价因子信息量图(坡形)

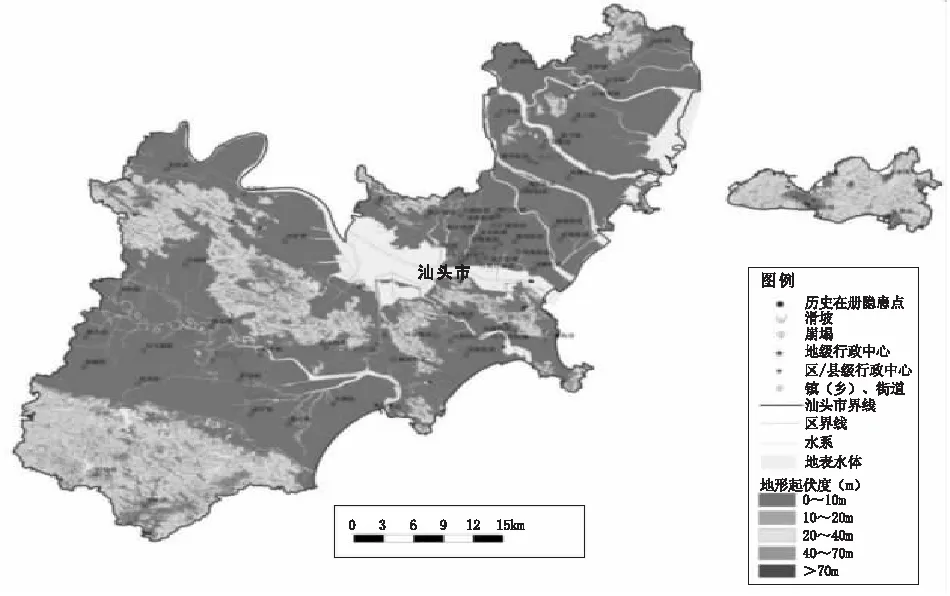
图3 地质灾害易发性评价因子信息量图(地形起伏度)

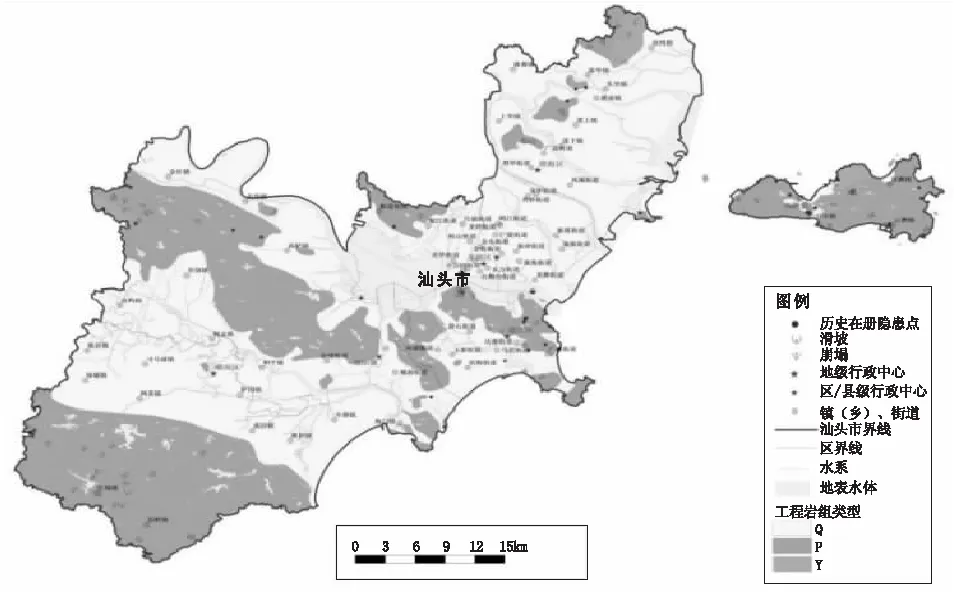
图4 地质灾害易发性评价因子信息量图(工程岩组)

图5 地质灾害易发性评价因子信息量图(地质构造)

3.4 评价结果

采用GIS空间分析中栅格重分类工具，按照自然断点分级法(表4)，找出4个突变点作为分区界限将地质灾害易发性结果图分为高易发区、中易发区、低易发区、非易发区4类。最后，在定量分区的基础上，综合考虑现有地质灾害各区分布、环境地质灾害条件及人类工程活动强度等各种因素，进行人工修正，得到最终的崩塌、滑坡地质灾害易发性分区图，详见图8。

图6 地质灾害易发性评价因子信息量图(距道路距离)

图7 地质灾害易发性评价因子信息量图(距水系距离)

表4 地质灾害易发性分区分级范围

图8 汕头市地质灾害易发性分区图

由图8可知，汕头市地质灾害高、中易发区主要集中在西部、中部部分地区以及东部地区。其余大部分地区的地质灾害的易发性以低易发区为主。对于中高易发区的崩滑流地质灾害，建议采用工程治理、监测预警的方式进行风险管控，以工程治理为主，监测预警以专业监测和群测群防相结合，专业监测为主。对于低易发区，采取保护性方法，防灾减灾对策以群测群防为主。