周期准互补序列集构造法

陈晓玉 彭秀英 王成瑞 崔 莉

(燕山大学信息科学与工程学院 秦皇岛 066004)

(河北省信息传输与信号处理重点实验室 秦皇岛 066004)

1 引言

传统互补序列集又称完备互补序列集(Perfect Complementary Sequence Set, PCSS)，是由多个完备互补序列组成，每个完备互补序列异相自相关函数值的和与互相关函数值的和为0[1,2]。由于其完备互补序列集具有理想的相关特性，因此可以有效消除通信系统中的多址干扰(Multi-Access Interference, MAI)和多径干扰(Multi-Path Interference,MPI)[3]。通常，一个完备互补序列用一个2维矩阵表示，完备互补序列的子序列组成矩阵的行。在实际应用中，首先给每个用户分配一条互补序列，然后子序列发送到子载波信道上进行扩频，最后多个载波信号叠加同时发送出去[4]。因此，互补序列的数量决定了系统所能支持的用户数[5]。然而，根据已有理论界可知，传统互补序列集的序列数量不能超过子序列数量，从而使系统所能支持的用户数受到了限制。

为了克服传统互补序列的缺陷以达到支持海量用户同时接入的目的，零相关区互补序列集[6–9]、低相关区互补序列集[10]和准互补序列集[11–14]的构造方法被提出。低相关区互补序列集(Low Correlation Zone Complementary Sequence Set, LCZCSS)是指在零点附近区域内异相相关函数值的和是一个很小的值，这个区域称为低相关区。当异相相关函数值为0时，被称为零相关区互补序列集(Zero Correlation Zone Complementary Sequence Set, ZCZ-CSS)。准互补序列集(Quasi-Complementary Sequence Set, QCSS)是在整个周期内异相自相关函数值的和与互相关函数值的和为一个很小的值δ(δ̸=0 ) 。值得注意的是，当δ=0时，序列集为完备互补序列集。LCZ-CSSs和ZCZ-CSSs的研究成果较为丰富，QCSSs的研究成果还相对较少。Liu等人[11]基于Singer差集构造了一类最优和一类几乎最优周期QCSSs。文献[12]改进了文献[11]的构造方法，基于差集和几乎差集提出了几类最优和几乎最优周期QCSSs的构造方法。文献[13]利用有限域上的加法和乘法特性提出了一种周期QCSS的构造框架，并基于这个框架给出了5种周期QCSSs的构造方法。文献[14]基于分圆类提出了一类渐近最优周期QCSSs的构造方法。

本文首先基于2元序列支撑集和低相关序列集提出了一种新的周期QCSS的构造框架。此框架构造的关键是找到一组合适的2元序列和低相关序列集，使2元序列长度L与低相关序列集长度N满足条件L|N。只要给定一组满足条件的序列集即可得到一类周期QCSS。其次，基于提出的框架结构，给出了3组满足条件的序列集，即2元m序列支撑集分别结合最优4元序列族A和族D；2元Sidelnikov序列支撑集结合Luke序列集，从而完成了3类周期QCSSs的构造。

2 基本概念

3 新的周期准互补序列集构造框架

分以下两种情况讨论序列间相关性。

情况1当0≤m1̸=m2≤M −1且τ=0时

综上两种情况可知，序列集C的最大相关函数幅值δmax=max{R1,R2}。 证毕

本节提出一种周期QCSS的构造框架，构造的目标序列集C的参数由2元序列a的支撑集和低相关序列集Q共同决定。构造的关键在于当给定一个具体的2元序列时，需要找到满足条件的低相关序列集Q，选取的序列不同，则构造的QCSSs的参数也不同。

4 周期准互补序列集的构造

4.1 基于2元m序列构造周期QCSS

本节在上述框架的基础上利用2元m序列支撑集分别结合最优4元序列族A和族D构造了两类渐近几乎最优周期QCSSs。

引理1[11]族A={v0,v1,...,v2n}是 包含2n+1个序列的集合。每个序列的长度为 2n −1，特别注意，序列v0是一个2元m序列且异相自相关函数值为−1。族A的最大相关函数幅值为

V={v1,v2,...,v2n}是族A的子集，且具有如式(13)的性质

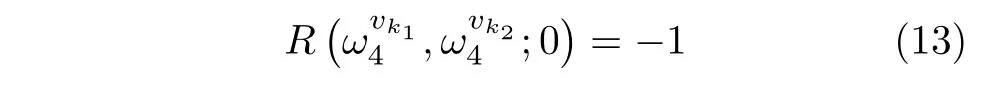
其中，1≤k1,k2≤2n。

引理2[11]族D={v0,v1,...,v2n−1}是 包含 2n个序列的集合，每个序列的长度为2 (2n −1)。族D的最大相关函数幅值为

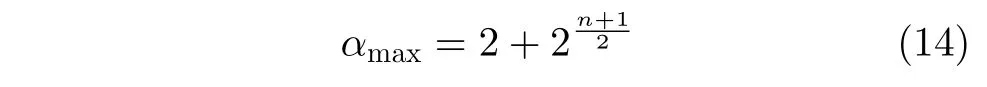
且族D具有如式(15)的性质

其中，0≤k1̸=k2≤2n−1,τ=0 或 者τ=2n −1。

引理3[13]设一个正整数n， 令q=2n,u=(u0,u1,...,uL−1) 是一个长度为L=q −1的2元m序列，对于任意的lmolL̸=0，则有

引理4[13]设序列a=(a0,a1,...,aL−1)是一个长度为L的2元序列，其中ai=(ui·vi)mod2， 序列u和序列v是长度为L的2 元m 序列。D={d0,d1,...,dK−1}为 序 列a的 支 撑 集，序 列a的 汉 明 重 量wt(a)=(1,1)=(L+1)/4 ， 则K=(L+1)/4，对于所有的lmolL̸=0有

方法1

步骤1 取一个正整数n，令L=2n −1，u和v是两个长度为L的2元m序列。构造一个2元m序列a=(a0,a1,...,aL−1)，其中

方法2

步骤1,2 同方法1。

步骤3 取最优4元序列族D作为框架步骤2中低相关性序列集，根据式(8)构造周期QCSS。

4.2 基于2元Sidelnikov序列构造QCSS

表1 方法1周期准互补序列集参数

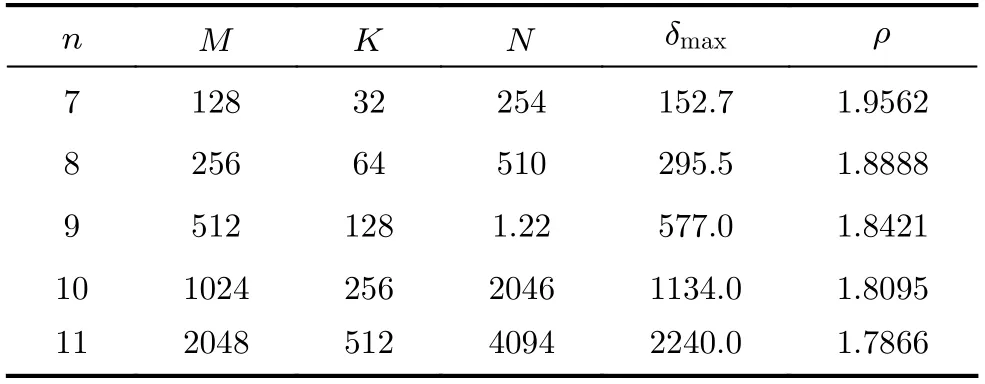
表2 方法2周期准互补序列集参数

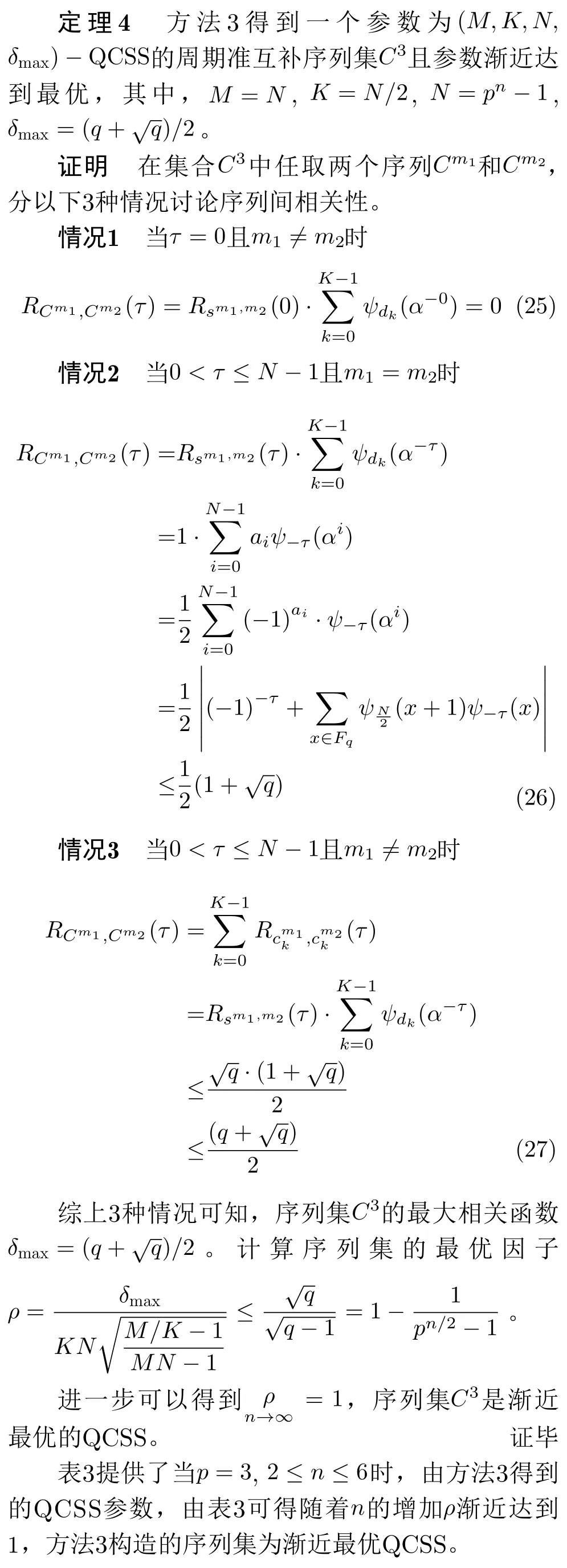
5 构造方法比较

表4对现有QCSSs的构造方法和本文的构造方法进行了比较。文献[11]利用Singer差集和序列的线性相位变化提出了一种周期QCSS的构造框架，本文方法1基于2元m序列支撑集分别结合最优4元序列族A和族D构造了两类渐近几乎最优的QCSSs。对比文献[11]，当QCSSs的子序列数目N相同时，本文方法1和方法2构造的序列数目M是文献[11]的2倍。在多载波扩频通信系统中，本文构造方法可以支持更多的用户。

表4 准互补序列集参数比

文献[12]拓展了文献[11]构造方法的思路，利用差集和序列的线性相位变换构造了两类渐近最优周期QCSSs；对比文献[12]，本文构造方法得到的序列数目呈指数形式增长，构造的序列数目更多，在多载波通信系统中，可以支持更多的用户。除此之外，文献[12]中参数p取不小于5的奇素数，而本文方法3中p的取值可以为任意的奇素数，参数选择范围更加的广泛，方法较文献[12]更加灵活。

文献[13]基于有限域上的加法和乘法特性提出了一种周期QCSS的构造框架，并在此框架下构造了5种具体的周期QCSSs。本文基于低相关序列集和2元序列支撑集提出了一种周期QCSS的构造框架。对比文献[13]，若本文构造框架中的低相关序列集取序列族S[15]，即可以得到文献[13]所提出的构造框架，可见文献[13]的构造框架是本文的一个特例。当其他满足条件的低相关序列集，如序列族A、族D和Luke序列集应用到本文框架中时，则可以得到更多具有不同参数形式的QCSSs，从而满足不同通信系统的要求。

6 结束语

本文提出一种新的周期QCSS的构造框架，在这个框架的基础上，基于2元m序列和2元Sidelnikov序列分别结合最优4元序列族A，族D和Luke序列集构造了3类周期QCSSs，序列集的参数由2元序列和低相关序列集共同决定。除此之外，本文所提QCSS构造框架包含了现有QCSS的构造框架，且构造的序列数目更多，在多载波扩频通信系统中可以支持更多的用户。

表3 方法3周期准互补序列集参数