风力机翼型仿生襟翼的结构参数优化设计及气动性研究

2022-11-29马祺敏王加浩张洋马列林健辉刘小民

西安交通大学学报 2022年11期

马祺敏,王加浩,张洋,马列,林健辉,刘小民

(1.西安交通大学能源与动力工程学院,710049,西安;2.广东美的制冷设备有限公司,528311,广东佛山)

风力机叶片是风力机的主要能量转换部件,其设计的优劣直接决定了风力机获取风能的效率[1]。对于叶片翼型而言,流动分离是翼型绕流中普遍存在的现象。流动分离会影响翼型的升、阻力并增加能量损失,还会引起翼型表面气动力的剧烈波动,限制风力机的安全与高效运行。因此,研究翼型的流动分离控制技术具有十分重要的意义。流动分离的控制技术主要有主动控制技术和被动控制技术,其中被动流动控制技术不需要引入外部能量,而是通过改变翼型表面流动的边界条件来优化流场结构[2]。

近年来,随着仿生学和流动控制技术的交叉融合,研究人员通过观察某些鸟类飞行和鱼类游动等特征,提出了抑制流动分离的仿生方法[3-4]。鸟类在着陆过程中或在阵风中,通过翅膀上表面的尾缘羽毛微抬来控制飞行姿态、提高飞行效率(图1)。因此,在大攻角来流和翼型气动性能急剧恶化的情况下,在翼型吸力面使用“弹出羽毛”型高升力装置(被动襟翼)可以抵消与动态失速相关的负面气动效应。研究人员采用实验和数值计算的方法对大攻角下的仿生襟翼翼型的气动性能以及襟翼的结构参数展开了研究[5-9]。其中,Revell等探究了10°攻角下刚性襟翼的长度、附着位置和展开角对翼型气动性能的影响以及不同参数设计下仿生襟翼气动性能的正、负效应[6]。Altman等在NACA-0012、USA-28和Eppler-423共3种不同翼型上安装相同结构的襟翼后发现,虽然添加襟翼后的3种翼型在失速后的气动性能均有提高,但并没有普遍适用的最优襟翼结构[7]。这也间接反映了相同的襟翼安装在不同翼型后会产生不同的气动效果。Robert等结合数值和实验方法,研究了翼型上添加自激活活动襟翼对二维翼型非定常流动的影响[8]。Johnston等比较了12°～20°攻角范围内翼型表面附加不同展开角度的自由移动襟翼和固定襟翼对气动性能的影响,发现襟翼的弹起角度小于60°时翼型获得最大升力[9]。

鸟类在特殊飞行条件下羽毛微抬的仿生理念大多只应用于微小型飞行器或者飞机机翼[10],而将该仿生襟翼应用于风力机翼型来抑制流动分离的研究相对少见。同时,以往襟翼结构参数的研究仅限于单一参数对翼型气动性能影响,未考虑襟翼结构参数之间的交互影响作用[11]。常规的襟翼结构优化方法主要为试错法,很难协同匹配出最优的襟翼结构参数组合。RSM在多元线性回归的基础上可以寻找目标函数与各参数因子间的定量规律,从而获得各参数因子水平的最佳组合[12]。基于此,本文以风力机S809翼型为基础,采用RSM对翼型仿生襟翼中的结构参数进行多参数协同优化设计,确定各结构参数及其交互作用对升阻比的影响,得到襟翼结构参数的最优水平组合,以此改善翼型表面的绕流状态,提高气动性能。本研究中的仿生襟翼可铰接在风力机叶片上表面,襟翼的弹起和关闭受到相应的液压驱动以及机械装置的控制。借助计算流体动力学从静态、动态气动特性两方面对仿生襟翼翼型和原始翼型的气动性能进行了对比,分析得到了大攻角下仿生襟翼翼型的流场变化和气动性能提升的原因,并说明了采用RSM来优化襟翼结构的有效性。

1 数值模拟

1.1 物理模型

本文选取风力机专用翼型S809作为基础翼型,这种翼型具有较高的升阻比和升力系数,被广泛用于研究风力机翼型气动性能的提升[14-15]。翼型弦长c设为1 000 mm,来流雷诺数Re=1×106。受鸟类在飞行失速时羽毛的自适应弹起现象启发,在S809翼型的上翼面添加仿生襟翼并建立相关几何模型,以提升大攻角下翼型的气动性能。图2为大攻角下S809翼型附加仿生襟翼弹起的二维结构示意图,对于仿生鸟类襟翼来说,其微抬羽毛的厚度特别薄,因此襟翼厚度按照文献[13]选为0.032c。至此,仿生襟翼的结构由3个参数决定,分别为襟翼高度H、襟翼到尾缘的距离D和襟翼弹起角度θ。随着攻角的变化,仿生襟翼的变化状态为:在低攻角下,仿生襟翼附着在翼型表面,对绕流气流不产生任何影响;随着攻角增加至失速攻角附近时,后缘区域出现流动分离,促使襟翼弹起。

1.2 控制方程

采用计算流体力学商业软件ANSYS Fluent 2021对翼型的气动性能进行数值求解。在风力机的实际工作条件下,气流流动马赫数较小,因此风力机翼型邻域流场中的流体可以视为不可压缩黏性流体。风力机叶片前的来流大小和方向随时间的不断变化使得动态失速现象普遍存在,进而造成翼型周围存在复杂分离现象。同时,动态失速流场与同工况下的静态流场有较大差别,因此采用静态数值计算和动态数值计算相结合的方法对翼型的气动性能进行求解。数值计算的控制方程采用二维不可压缩雷诺平均Navier-Stokes(RANS)方程

(1)

式中:ui是流体运动速度;p是压力;ρ0是密度;γ是运动黏度;fi是质量力。

1.2.1 静态数值计算与验证

使用压力速度场耦合求解动量方程与质量方程。计算采用压力基的隐式求解器和SIMPLE算法。基于RANS的湍流模型选取两方程模式的SSTk-ω模型[16]。在流动控制方程的数值离散中,控制方程的动量项以及黏性项均使用二阶迎风格式。如图3所示,S809翼型在攻角为0°时的计算域模型是由半径为10c的半圆与20c×20c的矩形组合而成,入口边界距离翼型前缘为10c,出口边界距离翼型尾缘为20c,上下边界与翼型相距为10c。翼型表面采用无滑移边界条件。计算域左侧边界以及上下边界为速度入口,来流速度为15 m·s-1;计算域右侧边界为压力出口,出口静压为0 Pa。翼型周围的流场采用C型结构化网格划分,为了提高翼型边界层区域流场的计算精度,近壁面第一层网格满足y+≤1,所以在网格划分过程中需要对翼型和襟翼进行局部加密,网格划分具体细节见图3。为了保证计算的收敛精度,控制流场内所有物理量的最大残差在10-6以下。基于以上计算条件对翼型在0°～25°攻角下进行静态求解。

以升力系数作为响应目标,随机选取10°攻角下的翼型计算域进行网格无关性验证,以此来消除网格数对计算结果的影响。不同网格数与升力系数之间的关系如图4所示,可以看出当网格数大于14万时,升力系数曲线基本稳定,波动误差在0.4%以内。最终选用计算域网格数为16万。

根据Somers等的实验结果[17]与Hao等的计算结果[18]对静态数值计算的准确性进行了验证。图5显示了攻角为0°～25°时翼型升力系数计算结果与实验结果的对比,可以看到本文计算结果与上述结果吻合良好,而在大攻角下,翼型处于失速工况,失速后引起的三维效应较强,导致大攻角下的模拟值与实验值相差较大,但计算所得升力系数随攻角的变化趋势仍与实验一致。在大攻角下,相比于Hao等的计算结果[18],本文的计算结果与实验结果[17]吻合度更高。因此,本文计算模型有效,可用来预测二维翼型的气动性能。

1.2.2 动态数值计算与验证

翼型的动态数值计算仍然采用静态数值模拟中的结构化网格,并采用滑移网格模型。定义翼型绕翼型前缘点在0°～25°攻角范围内做周期性振荡,攻角的变化形式为

α(t)=α0-Δαcos(2πft)

(2)

式中:α(t)为瞬时攻角;α0为平均攻角;Δα为振幅攻角;f为翼型的周期振荡频率;t为做周期振荡的时间。

为表征振荡运动对主流运动影响的大小,在翼型的周期性振荡运动中引入了一个描述翼型运动的非定常性无量纲参数换算频率

(3)

式中u∞为来流速度。

翼型的动态失速特征主要由平均攻角α0、振荡幅度Δα以及换算频率k这3个参数所决定。本文动态失速工况为:α0=14°,Δα=10°,k=0.05。为保证计算准确性,以定常计算得到的收敛解作为初始流场进行非定常流动计算,计算模型仍采用SSTk-ω模型,计算时间步长dt为0.000 67 s。图6给出了S809翼型升力系数在计算过程中的周期性演变,在第一个俯仰周期之后,升力系数开始出现周期性振荡。因此,本文选取第3个俯仰周期内的计算数据用于分析。此外,为验证本研究中动态计算结果的准确性,将翼型动态计算结果与Ramsay等[19]的实验结果和Hu等[20]的计算结果进行对比分析,结果如图7所示。可以看出,本文计算结果与上述结果吻合较好,说明采用该计算方法得到的非定常结果具有较高的准确性。

2 仿生襟翼的响应面优化设计

2.1 响应面方法

响应面(RSM)是由实验设计、回归分析和非线性优化等综合而成的一种优化方法。它采用多项式回归技术对实验数据进行最小二乘法拟合,从而建立起多因素响应问题,然后依据模型对影响因素进行非线性优化,得到各因素与设计目标的响应关系以及设计目标的最优值[21]。

2.2 实验设计及响应面模型建立

由于风力机叶片在失速之后气动性能会降低,本文采用附加仿生襟翼结构主要用来改善大攻角下的翼型气动性能。因此,选择大攻角下对仿生襟翼结构进行响应面优化设计更有效果,且由于14°攻角接近于翼型静态失速攻角,故本设计选取14°攻角进行研究。选取仿生襟翼高度H、襟翼到尾缘的距离D、襟翼弹起的角度θ这3个参数作为实验设计因子。考虑到Box-Behnken实验设计方法样本空间少、效率高的优点,本研究采用Box-Behnken方法进行实验设计。根据实际设计经验,设计变量的取值范围为:θ=10°～30°,D=0.2%c～0.4%c,H=0.05%c～0.2%c。

根据以上因子取值范围,为简化计算,将各因子转化为编码变量。各因子水平见表1。

表1 影响因子水平

由于翼型气动特性的指标中升阻比更能反映翼型的综合气动性能,因此本研究选取升阻比作为响应。根据Box-Behnken实验设计方法所得到的17组实验样本空间及各方案的实验结果如表2所示。

表2 实验方案及结果

采用最小二乘法对上述实验设计方案及结果进行回归方程的二次多项式拟合,得到基于上述影响因子及其交互效应与响应的函数关系如下

G=-45.19+3.64A+64.41B+428.05E-
2.06AB-10.95AE-224.80BE-0.04A2-
36.03B2-473.40E2

(4)

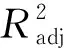
因此,根据检验式(4)中的数学模型,最优翼型升阻比所对应的襟翼结构的各参数分别为:θ=12.35°,D=0.2%c,H=0.2%c。

3 结果分析

3.1 静态气动特性结果分析

将上述RSM方法得到的最佳襟翼结构应用于1.2.1小节的数值计算模型中,计算所得到的原始翼型、可弹起襟翼翼型和固定襟翼翼型在0°～25°攻角下的静态气动特性曲线如图8所示。

图8(a)为3种翼型的升力系数随攻角的变化。在0°～11°攻角下,固定襟翼翼型与原始翼型相比升力系数均减小,而闭合状态的可弹起襟翼翼型的气动性能较原始翼型基本不变。随着攻角逐渐增大,当攻角为11°时,可弹起襟翼翼型的襟翼弹起。因此,从12°攻角开始,可弹起襟翼翼型与固定襟翼翼型的升力变化一致,且可弹起襟翼翼型的升力系数较原始翼型均得到了提升。其中,可弹起襟翼翼型在攻角为14°时的升力较原始翼型提升最大,相对于原始翼型提升了13.67%,并且该攻角也是最优襟翼结构的设计攻角,间接说明了响应面设计方法提升襟翼气动性能的有效性。图8(b)给出了3种翼型阻力系数的对比,固定襟翼翼型在0°～11°攻角下的阻力系数均高于原始翼型,并且攻角越小,固定襟翼翼型的阻力系数越大。当攻角大于11°时,可弹起襟翼翼型和固定襟翼翼型的阻力系数开始低于原始翼型。攻角14°时可弹起襟翼翼型和固定襟翼翼型的阻力相比于原始翼型降低了3.98%。图8(c)给出了3种翼型的升阻比的对比。当攻角α在0°～11°时,固定襟翼翼型的升阻比明显低于原始翼型。当攻角大于11°时,可弹起襟翼翼型和固定襟翼翼型的升阻比开始高于原始翼型,在攻角α=13°时,升阻比提升最大,较原始翼型提升了53%。同时,从图8可以看出,可弹起襟翼翼型和固定襟翼翼型失速点较原始翼型后移,这说明了襟翼结构对翼型在大攻角下的失速特性也有积极的改善作用。

上述分析表明,在大攻角下仿生襟翼可以明显提升翼型的升力并且降低阻力,并改善翼型在大攻角下的失速特性。RSM模型所预测的最优襟翼结构在14°攻角时的升阻比为26.81,数值计算结果为26.60,相对误差为0.78%,RSM方法预测的翼型升阻比与数值计算结果较一致,说明RSM方法的较高预测精度以及RSM方法用于优化襟翼结构的合理性。

为进一步探究大攻角下优化仿生襟翼翼型气动性能提升的原因,图9显示了14°、18°和22°攻角下原始翼型与仿生襟翼翼型邻域流线及速度的分布情况。当α=14°时,原始翼型尾缘发生了流动分离现象,在翼型吸力面后缘出现了一个较大的分离涡,而襟翼会对流体产生阻挡作用,迫使流体改变运动方向,将吸力面后缘处大分离涡分割成为小的涡团,所以在α=14°时仿生襟翼翼型除了吸力面的分离涡以外,还有位于襟翼尾缘的旋向相反的小分离涡以及位于襟翼与翼型吸力面之间的均匀分布的5个小尺度角涡。由于襟翼对吸力面分离涡的分割作用,吸力面的分离涡的体积比原始翼型分离涡体积更小。同时,仿生襟翼对来流的阻挡作用限制了分离涡向翼型尾缘移动,因此原始翼型上翼面分离涡的涡心位置较仿生襟翼翼型更靠近翼型尾缘。当攻角逐渐增加至18°时,原始翼型与仿生襟翼翼型尾缘处的分离涡均明显增大,分离层加厚并向翼型前缘靠近,分离涡的涡心沿着吸力面向后方移动并且逐渐远离吸力面,襟翼尾缘的旋向相反的小分离涡逐渐后移并变大。与原始翼型相比,仿生襟翼翼型吸力面上分离涡体积更小。当α=22°时,原始翼型与仿生襟翼翼型吸力面上的分离涡已经完全覆盖了翼型的吸力面。仿生襟翼翼型吸力面与襟翼之间的5个小尺度角涡也汇聚成为了一个相对较大的角涡。

为进一步验证在大攻角下采用优化仿生襟翼对翼型气动性能提升的有效性,将原始翼型和仿生襟翼翼型沿展向延伸,建立了原始翼型和仿生襟翼翼型的三维计算模型,如图10所示。图11为原始翼型与仿生襟翼翼型的三维模型气动性能对比。在0°～11°攻角下,由于仿生襟翼处于闭合状态,附加襟翼翼型的升、阻力特性较原始翼型基本不变。α=11°时襟翼弹起,随着攻角的继续增加,附加襟翼翼型的升力系数均高于原始翼型,阻力系数均低于原始翼型。这说明了在大攻角情况下,附加襟翼使得翼型的气动性能得到了改善,这与二维翼型的升阻力特征变化基本一致。因此,上述结果验证了该优化襟翼结构在三维叶片中同样具有改善翼型气动性能的作用。

湍动能是湍流强度和流体能量耗散的指标。图12选取了α=14°,18°时两种三维叶片的湍动能分布情况。由图可知,仿生襟翼翼型尾缘后方的高湍动能区域与原始翼型相比明显减小,说明仿生襟翼减弱了尾流中间区域以及翼型尾缘后方的湍动能。因此在大攻角条件下,仿生襟翼能够抑制湍流脉动,从而提高翼型气动性能。具有二维结构特征的仿生襟翼的优化设计对三维模型的气动性能提升也同样有效。

3.2 动态气动特性结果分析

为了进一步对仿生襟翼翼型气动性能的影响进行深入研究,根据上述动态计算模型对可弹起襟翼翼型、固定襟翼翼型与原始翼型进行了动态气动特性的计算,动态特性下的升力系数和阻力系数的迟滞曲线如图13所示。基于襟翼的工作状态,动态工况下的仿生襟翼翼型上襟翼的弹起角度为14°。在上仰过程中,固定襟翼翼型在α=4°～14°之间的升力系数低于原始翼型和可弹起襟翼翼型;当α>14°后,固定襟翼翼型和可弹起襟翼翼型升力系数均高于原始翼型;当α=18°时,固定襟翼翼型和可弹起襟翼翼型的升力系数取得了最大值,较原始翼型提升了25.85%。在下俯过程中,当α=4°～10°时,固定襟翼翼型的升力系数低于原始翼型和可弹起襟翼翼型;当α>1°后,固定襟翼翼型和可弹起襟翼翼型升力系数均高于原始翼型;当α=21°时,固定襟翼翼型和可弹起襟翼翼型的升力系数最大,较原始翼型提升了41.8%。根据图13(b)可知:在下俯运动过程中α=4°～10°时,固定襟翼翼型的阻力系数略高于原始翼型和可弹起襟翼翼型;在α>10°时,固定襟翼翼型和可弹起襟翼翼型的阻力系数与原始翼型几乎一致,但在上仰过程中固定襟翼翼型和可弹起襟翼翼型的阻力系数均小于原始翼型。上述分析表明,可弹起襟翼翼型相比于固定襟翼翼型能够避免小攻角时襟翼对翼型气动性能造成的负面影响,而在大攻角时,弹起襟翼使得翼型的气动性能得到提升。

图14为大攻角下仿生襟翼翼型和原始翼型做俯仰运动时的瞬时涡量分布云图。在翼型上仰过程中,α=14°时的涡量几乎覆盖了仿生襟翼翼型和原始翼型的整个表面,但较大的涡量主要集中在翼型的后半部分和上翼面周围。在静态工况下,翼型的失速攻角约为14°,但是在动态工况下翼型上仰至14°还没有出现明显的流动分离,这说明动态失速工况下翼型上仰阶段的失速攻角被延迟。当翼型上仰至α=20°时,原始翼型与仿生襟翼翼型的表面出现了明显的流动分离现象,翼型吸力面的尾缘出现了较为明显的分离涡。由于襟翼的作用,仿生襟翼翼型的分离涡仍保持较好的附壁效果,并且尾缘的两个相干分离涡也明显减小,这解释了图13中仿生襟翼翼型在α=10°～22°范围内升力大幅提升的原因。随着翼型进一步上仰,翼型尾缘处的分离涡逐渐向前缘移动,当上仰攻角增加到24°时,仿生襟翼翼型与原始翼型吸力面的分离涡和翼型尾缘的尾涡面积明显增大,并且流动分离情况加剧,这也是图13的动态气动曲线中翼型的升力急剧下降和阻力波动的原因。在翼型逐渐下俯过程中,上述两个涡结构依然存在。与α=24°相比,α=20°时原始翼型与仿生襟翼翼型吸力面的分离涡减小、尾涡增大。仿生襟翼翼型吸力面的分离涡和尾涡均分裂成两个,并逐渐脱离向翼型后方移动,而且仿生襟翼翼型的分离涡包裹了位于翼型尾缘的尾涡,限制了尾涡的产生与发展,因此仿生襟翼翼型的尾涡较原始翼型小。当翼型下俯至α=14°时,附着在两种翼型表面和尾缘的分离涡脱落,同时在上翼面有分离涡重新生成。原始翼型在α=14°已经发生明显的流动分离,而仿生襟翼翼型表面的分离涡仍为附着流动状态,使得翼型的动态失速延迟,涡结构的变化是导致翼型的动态气动特性变化的主要原因。