某8×8越野车转向系统特性分析及优化

王佩佩,王昱杰,陈 莉,雷 宇

(1.武汉理工大学 研究生工作部，湖北 武汉430070；2.武汉理工大学 国际教育学院，湖北 武汉 430070；3.东风越野车有限公司，湖北 十堰 442013；4.武汉理工大学 自动化学院，湖北 武汉 430070)

多轴越野车由于兼顾了承载能力与越野能力，有利于实现军用车辆“机动-防护-火力”三方面的平衡，得到了世界各军事强国的青睐，纷纷发展了自己的多轴越野承载平台。美军发展了“斯特赖克”系列车型，德国推出了“拳击手”[1]，法国雷诺公司则推出了VBCI轮式步战车[2]，中国陆军则推出了ZBL-08战车[3]。

相对于常规车辆，多轴车辆的整车长度较大，转弯半径大。越野车对机动性的高要求，希望车辆转弯半径尽可能小，因此该类型车辆发展了多轴转向技术。包括第一二轴转向[4]、第一四轴转向、全轮转向等。采用多轴转向系统后，车辆的操纵稳定性也随之受到影响，因此众多研究人员在常规车辆稳定性控制的基础上进行拓展，采用主动转向控制(ASC)[5]，防侧翻控制(RSC)[6]和直接横摆力矩控制(DYC)[7-8]等方法对车辆在不同行驶工况下的稳定性进行分析和改善。但缺少对转向方式进行系统对比的研究。王旭冉[9]研究了采用轮毂电机的多轴越野车的稳定性，并通过DYC与阿克曼转向相结合的方式降低车辆的转弯半径。彭博等[10]结合后桥差动制动对车辆的转向性能进行改善。南海峰等[11]对多轴越野车的不同转向模式进行综述分析。针对车辆的稳定性控制，研究人员基于比例微分积分控制器(PID)[12]、滑模控制器(SMC)[13]和线性二次型调节器(LQR)[14]、模型预测控制(MPC)[15]等方法开展了相关研究，以主动转角控制、制动/驱动控制产生附加横摆力矩、主动悬架作动等方式对车辆的状态进行调整以改善车辆的稳定性，大部分研究的对象为二轴车辆。通常使用单、双轨二自由度模型对车辆性能开展理论分析，并以此作为参考模型，制定控制策略对车辆的稳定性进行优化。相关研究能为多轴越野车的稳定性控制提供参考。

笔者基于车辆动力学，搭建了多轴越野车的二自由度模型，基于某越野车的参数，对采用第一二轴转向、一四轴转向两种转向方式的系统特性进行了对比。并设计了车辆的稳定性控制器对车辆转向过程中的稳定性进行控制，通过搭建整车动力学模型，对车辆有、无控制情况下的车辆的动力学响应进行对比，为该类车辆在转向系统的设计提供了参考。

1 模型搭建

车辆是复杂的多自由度系统，因此，在研究中需根据研究目的，对车辆模型进行简化。二自由度模型能表征车辆的横向和横摆运动，通常在设计阶段用于对车辆的稳定性进行分析，在控制领域，则作为控制系统的参考模型使用。

单轨二自由度模型的假设如下：

(1)忽略车辆的侧倾、俯仰、垂向及纵向的自由度，仅保留体现车辆稳定性横向及横摆自由度。

(2)车辆在行驶过程中车速保持恒定。

(3)左右侧轮胎特性保持一致，并在行驶过程中始终处于线性区域。

典型的多轴越野车如图1所示，单轨二自由度模型如图2所示。

图1 多轴越野车

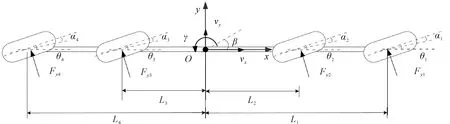
图2 多轴越野车单轨二自由度模型

根据汽车动力学知识，可得到车辆的横向和横摆自由度，分别如式(1)和式(2)所示。

Fy3cosθ3+Fy4cosθ4

(1)

L3Fy3cosθ3-L4Fy4cosθ4

(2)

式中：m为整车质量；vx、vy分别为纵向、横向速度；Fyi为轮胎的横向力；θi为车轮转角；Li为车轴到质心的距离，其中i=1,2,3,4。

Fyi=kiαi

(3)

式中：ki为轮胎侧偏刚度；αi为轮胎侧偏角。

根据图2中的几何关系，各轮胎的侧偏角αi与车辆质心侧偏角β、横摆角速度γ及车轮转角θi的关系如式(4)所示。

(4)

由于车轮转角θi较小(θi≤15°)，通常认为cosθi∈[0.97，1]≈1，则可根据式(1)～式(4)得到该车的状态空间方程，如式(5)所示。

(5)

X=[βγ]T

(6)

A=

(7)

(8)

U=[θ1θ2θ3θ4]T

(9)

2 转向系统性能对比

采用多轴转向系统可以有效减小车辆的转弯半径，但由于车轮转向将导致车内空间减小，影响车辆的空间承载能力。为降低系统复杂度，提升可靠性，多轴越野车的多轴转向系统多采用机械联动转向结构，三四轴联合转向将进一步增加系统的复杂度。因此，笔者结合相关研究，以第一轴转向为基础，对第一二轴转向及一四轴转向方案进行对比。为减少轮胎的磨损，各轴转角设置为比例关系，第一二轴车轮转角系数和第一四轴转角系数如式(10)和式(11)所示。

θ2=b1θ1

(10)

θ4=b4θ1

(11)

第一轴转向时，θ2=θ3=θ4=0，第一二轴转向时，θ3=θ4=0，第一四轴转向时，θ2=θ3=0。

根据式(5)～式(9)可得3种转向方案的横摆角速度增益，如式(12)～式(14)所示。

(12)

(13)

(14)

式中：k=k1+k2+k3+k4。

研究对象车辆的相关参数如表1所示，将其分别代入式(12)～式(14)对3种转向方式的横摆角速度增益进行对比，如图3所示。

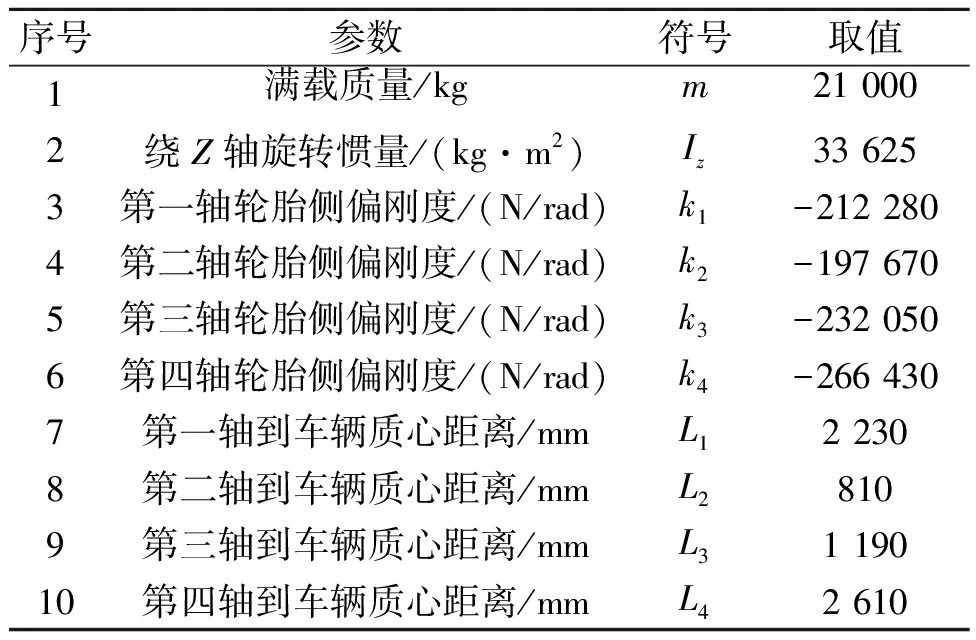
表1 车辆主要参数

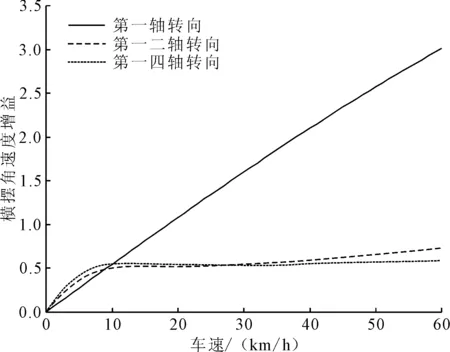
图3 横摆角速度增益对比

由图3可知,采用第一轴转向方案的横摆角速度增益随车速的增加而增加，在车速较低时，增益小于其它两种转向方式，超过该车速，该方案的横摆角速度增益大于其它两种方案。采用第一二轴转向与一四轴转向方案横摆角速度增益先随车速增加而增大，在超过一定车速后增速迅速降低。采用第一二轴转向方案横摆角速度增益在车速低于25 km/h范围内，略低于采用第一四轴转向方案的横摆角速度增益。

当车速趋于稳定时，转弯半径可由车速及横摆角速度计算得出，如式(15)所示。

(15)

3种转向方式在不同车速下的转向半径如图4所示。

图4 转向半径对比

由图4可知，采用3种转向方式的转向半径均随车速增加而增加，在相同车速下，采用第一四轴转向的转向半径最小，采用第一轴转向的转向半径最大。

采用第一四轴转向的转向系统性能优于其它两种转向方式。因此，选择该转向方式对车辆的转向系统进行设计并通过对车辆转角的补偿对车辆的转向稳定性进行控制。

3 自适应稳定性控制器设计

多轴越野车的稳定性控制架构如图5所示。首先以驾驶员输入到车辆的车速及方向盘转角输入到二自由度模型(参考模型)，计算理想横摆角速度和质心侧偏角。然后根据观测到的实车响应对车辆的稳定性状态进行判断。最后根据稳定性状态对线性二次型调节器(LQR)中的参数进行自适应调节，形成自适应线性二次型调节器(ALQR)，计算输入到车辆的补偿转角。通常以车辆的质心侧偏角表征车辆的安全性，横摆角速度表征稳定性，根据状态观测器观测到的车辆横摆角速度和质心侧偏角，对LQR控制器的Q、R矩阵进行调节，在保障车辆安全性的前提下完成稳定性的控制。

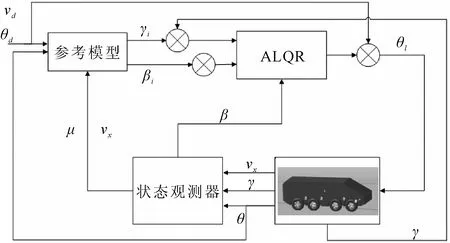
图5 自适应LQR控制架构

车辆的横摆角速度增益可由式(14)计算得到，但考虑到通过轮胎提供到车辆的横向力不能超过道路所能提供的最大摩擦力，横摆角速度的最大值可通过式(16)～式(17)计算得到。

(16)

(17)

结合式(16)、式(17)可得到车辆的理想横摆角速度如式(18)所示。由式(5)～式(9)可得到车辆的理想质心侧偏角，如式(19)所示。

(18)

(19)

车辆的最大质心侧偏角与道路附着系数μ及重力加速度g的关系需满足式(20)～式(21)。

|βimax|≤atan(0.02μg)

(20)

βi=min{|βg|,atan(0.02μg)}sgn(θ1)

(21)

设置LQR控制器的步长为T，选择双线性离散方法将连续的状态空间方程转化为离散系统，以对该系统进行控制。

x(k+1)=Adx(k)+Bdu(k)

(22)

式中：Ad=(I-TA/2)-1(I+TA/2)；Bd=TB；x(k)为系统时刻的状态量，u(k)为相应的控制量。该控制器的目的不仅要减小车辆的稳定性控制指标间的误差，还要保持控制量尽可能小。因此，目标函数如式(23)所示。

(23)

式中：正定矩阵Q、R分别为状态量x(t)和控制量u(t)的权重矩阵。控制律如式(24)所示。

u(t)=-R-1BTPx(t)=-Kx(t)

(24)

式中：P为式(25)Riccati方程的正定解，P的计算如式(25)所示。

PA+ATP-PBR-1BTP+Q=0

(25)

4 转向稳定性控制性能验证

转向半径是评价多轴越野车机动性的重要指标，转向系统同时对车辆的操纵稳定性有直接影响。为对采用不同转向方式的车辆的操纵稳定性进行评价，建立了Simulink-Recurdyn联合仿真模型，如图6所示，对车辆在双移线工况和鱼钩工况下的响应进行对比。双移线工况和鱼钩工况是评价车辆操纵稳定性的最常用工况。

图6 多轴越野车模型

在双移线工况中，车辆须以一定车速从原车道换道到平行车道再换回原车道，在此过程中，车辆不能触碰到ISO-3888-1-2018和GB/T 40521.1-2021[16]中所规定的边界。根据该标准中推荐的车速，对有无ALQR控制器的模型开展双移线仿真，车辆的横摆角速度、质心侧偏角及行驶轨迹对比分别如图7～图9所示。

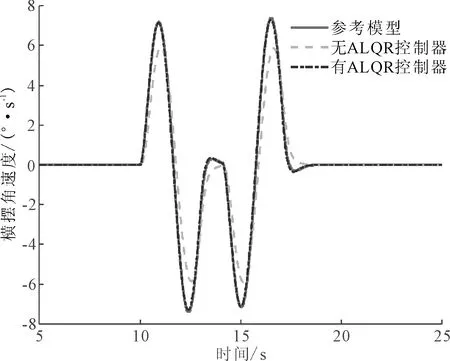
图7 横摆角速度对比

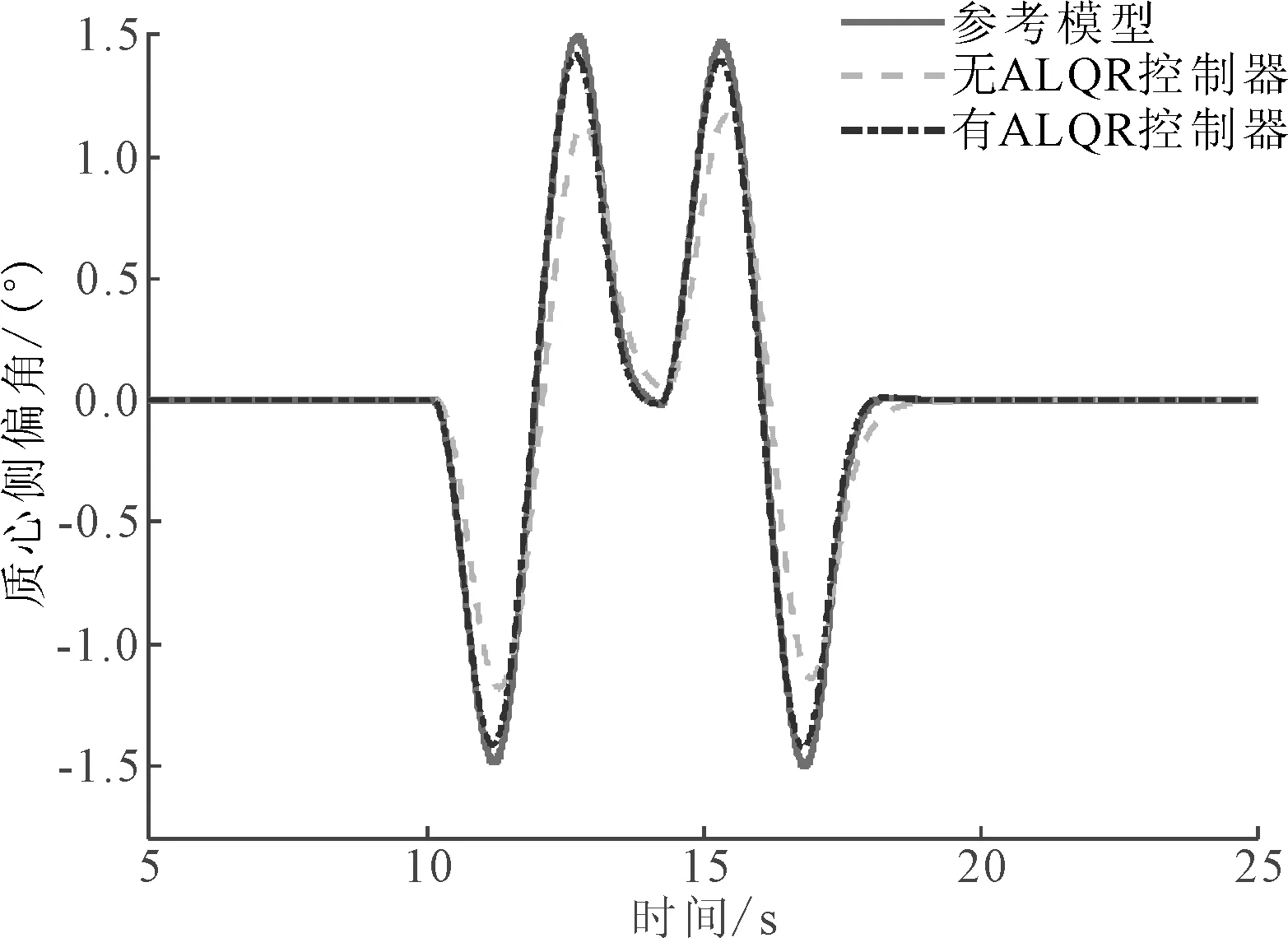
图8 质心侧偏角对比

图9 车辆轨迹对比

图7、图8中，有、无ALQR控制器与参考模型的横摆角速度和质心侧偏角变化趋势一致，但相对无控制器情况，有控制器和参考模型的横摆角速度与质心侧偏角间的误差较小，说明有控制策略后车辆按照预定轨迹行驶的能力更强。无控制器模型的输出结果与参考模型的主要差异体现在峰值绝对值较参考模型更小，从峰值到0，趋于0的时间更长。由图9可知，有控制与参考模型的行驶轨迹较为接近，差异在于最大横向位移误差为0.2 m，但有控制模型仍能通过双移线测试。无控制模型由于横向位移与参考模型差值较大(0.8 m)，且换道过程中行驶轨迹与参考模型也存在差异，不能通过双移线测试。

5 结论

(1)通过建立多轴越野车的3种转向方式的动力学模型，对采用第一轴、第一二轴及第一四轴转向三种转向方式的性进行对比。采用第一二轴转向一四轴转向的横摆角速度增益较接近，采用第一四轴转向的转向半径最小。

(2)以第一四轴转向建立了联合仿真模型，设计了车辆转向稳定性的自适应控制器，对车辆的稳定性进行提升。仿真结果表明，有自适应控制器的情况下，车辆能通过双移线测试，测试过程中，车辆的横摆角速度和质心侧偏角相对参考模型误差较小。无控制器的情况下，车辆不能通过双移线测试。因此，采用基于LQR的自适应控制器，能有效提升该车辆的转向稳定性。

(3)通过对多轴越野车的3种转向方式的分析和稳定性控制器的设计，可为该类车辆转向系统的设计提供参考，但在实际应用中，还应综合考虑整车操纵稳定性指标和车辆布置空间的需求，对多轴越野车的转向系统开展设计。