基于深度学习的金融时序数据分析研究
2022-11-28李慧玲
李慧玲
(国网河北省电力有限公司 信息通信分公司,河北 石家庄 050020)
时间序列数据的分类和预测在不同的领域得到了广泛的研究[1-2],现已广泛应用于自然语言处理、医学数据分析、气象学、金融等领域[3-6]。金融市场因其复杂动态特点,观测数据具有高度的非平稳性和噪声性,使得金融时间序列预测成为时间序列预测中最困难的任务之一。
在过去的几十年中,人们提出了许多数学模型,从噪声、非平稳的金融时间序列中提取金融特征。张劲帆等[7]提出了基于贝叶斯估计的混合频率向量自回归模型,并对该模型预测中国宏观经济运行情况的效果进行了检验。宋玉平等[8]通过自适应过滤法优化对以沪深300指数对数收益率及个股三一重工的收盘价为代表的五分钟高频金融时间序列进行预测。为确保数据的可处理性,这些模型通常假设基础数据分布是一定的,这导致对未来观测数据的泛化能力较差。近年来,随着机器学习技术的发展,有学者将其引入金融时间序列预测问题,从而减轻对数据分布假设的依赖。曹杨丽等[9]提出了基于支持向量回归的窗口平均预测方法,并将其应用于预测我国股指期货与股票市场相关性的影响。闫政旭等[10]提出了一种基于Pearson系数的随机森林新的组合模型方法,预测股票的走向趋势,解决了在大量特征和大数据下预测精度低的问题。陈学彬等[11]基于深度学习方法对信用债个体违约风险进行及时跟踪和预测。刘翀等[12]提出了基于深度LSTM和注意力机制的金融数据预测模型,解决了数据间长依赖的问题,并能学习更加复杂的市场动态特征。尽管机器学习模型推动了金融领域预测及分析技术的发展,但这些模型并不是为捕获时间序列数据中的时间信息而专门设计的。此外,部分深度学习模型通过引入注意机制提高了模型的性能和可理解性,但使模型更加复杂,从而带来更高的计算开销,阻碍了深度学习模型在金融领域的推广及实际应用,因此提出一种运算速度快,能够对连续的大量输入数据进行有效预测的模型具有重要的现实意义。
为提高网络模型训练效率,提出了一种结合双线性投影思想的神经网络层来学习多元时间序列数据。此外,在网络中引入注意增强双线性层(bilinear layer,BL)模型,使得模型可以用任何小批量梯度下降学习算法进行训练。
1 相关概念
矩阵X∈RD×T为一个二阶张量,D和T分别是维数。Xi∈RD×T,i=1,2,…,N,为由N个样本组成的集合,每个样本包含与其T列相对应的T个过去观测序列。过去值(T)的时间跨度称为历史,而想要预测的未来值(H)的时间跨度称为预测视界。例如,假设股票价格每秒钟和每周一次抽样Xi∈R10×100包含上一个T=100 s的不同限价指令簿(limit order book,LOB)水平的股票价格,预测范围H=10对应于预测下一个10 s的未来价值,即中间价。
1.1 注意力机制

(1)
(2)
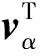
(3)
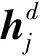
(4)
式中:Wout为参数,bout为偏置。
1.2 多元时间序列回归模型
基于双线性映射的回归模型描述如下:
f(X)=W1XW2
(5)
式中:X∈RD×T为一个包含T个时间步长的多元时间序列;W1∈R3×D和W2∈RT×1为要估计的参数。
通过学习将输入LOB状态转换为类成员向量的两个独立映射(大小为3×1,分别对应于中间价的3种类型的变动)。
2 模型构建
2.1 双线性层
令X=[x1,x2,…,xT]∈RD×T表示双线性层BL的输入。根据双线性映射回归模型,BL层将通过应用以下映射将大小为D×T的输入转换到大小为D′×T′的矩阵:
Y=φ(W1XW2+B)
(6)
式中:W1∈RD×D′,W2∈RT×T′,B∈RD′×T′为要估计的参数,φ(·)为元素非线性变换函数,如ReLU或sigmoid函数。
对于多层感知器[14](multilayer perceptron,MLP)层,将D×T大小的输入转换为D′×T′需要估计(DT+1)D′T′个参数(包括偏置项),这远高于BL的参数数目(DD′+TT′+D′T′)。同时,为了将映射应用于时间序列数据,将X的每一列和每一行分别表示为xct∈RD(t=1,2,…,T)和xrd∈RD,(d=1,2,…,D)。给定输入时间序列X,第t列表示在时间实例t处观察到的D个不同特征,第d行包含在过去t个步骤期间第d个特征的时间变化。在时间实例t=1,2,…,T时不同特征之间的相互作用由W1反映:
W1X=[W1xc1,W1xc2,…,W1xcT]
(7)
(8)
其中:W2反映第d个特征的时间进程。例如,假设X包含历史T期间D个不同LOB水平的股票价格,则BL通过W1确定不同股票价格在特定时间如何相互作用,以及通过W2确定特定指数的价格如何随时间推移。因此,利用LOB中存在的空间结构,可以更好地联合分配未来最佳买卖价格。
2.2 时间注意增强BL模型
尽管BL根据每个特征学习独立的依赖关系,但是不清楚一个时间实例的表示如何与其他时间实例交互,或者哪些时间实例对视界T′处的预测是重要的。通过将位置信息纳入注意力计算方案,学习模型仅使用过去序列中的特定时间实例来预测给定视界下的未来值,以便进行序列间学习。提出了映射输入X∈RD×T到输出Y∈RD′×T′的时间注意增强BL模型,具体如下所示:
(9)
(10)
(11)
(12)
(13)
式中:αij和eij分别为A和E位置(i,j)处的元素;为元素级多重复制算子;φ(·)为一个预定义的非线性映射;W1∈RD′×D,W∈RT×T,W2∈RT×T′,B∈RD′×T′及λ为所提注意增强BL模型的参数。与前面提到的基础BL模型类似注意增强BL模型通过W1和W2建立了独立的依赖模型,且通过W和λ学习中间注意过程。注意增强BL模型流程图,如图1所示:
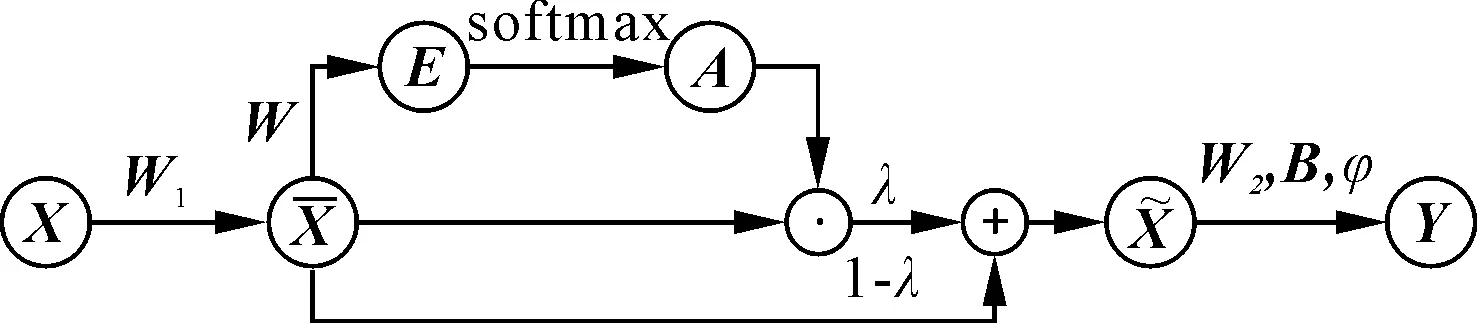
图1 注意增强BL模型流程图
具体可分为5个步骤:
(1)结合式(9),W1用于将X(每列)的每个时间实例xct,t=1,2,…,T,表示转换为新的特征空间RD′。该模型沿着X的第一个模式建立依赖关系,同时保持时间顺序不变。
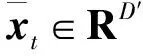
(3)结合式(11)中的softmax函数对E中的重要值进行归一化处理。该层将许多元素推向接近零的位置,同时将其中少数元素的值保持为正。该过程将产生注意力掩码A。
(4)从步骤(3)可得注意掩码A以消除RD′中不重要元素的影响。式(12)中的λ允许模型学习一种软注意机制,而非传统的硬注意机制。考虑到在学习过程的早期阶段,从前一层提取的学习特征可能是有噪声,并且可能不具有辨别性,硬注意机制可能会将模型误导到不重要的信息,而软注意可能会使模型在早期即在选择最重要的特征之前学习辨别特征。需注意,λ的范围为[0,1]之间;
(5)与BL模型类似,估计时间映射W2,并在偏置和非线性变换之后提取更高级别的特征。
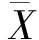
2.3 网络结构
输入为一个大小为40×10的矩阵,表示买卖双方前10个订单的价格和数量(40个值)。120×5-BL表示输出大小为120×5。网络结构如图2所示。
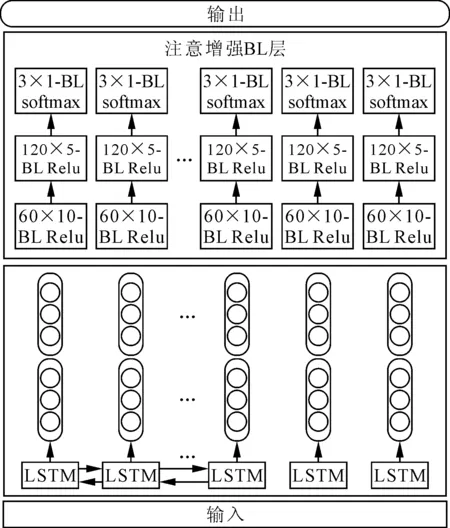
图2 网络结构
虽然注意机制可以放在任何一层,但网络参与高级表征更为有利,该过程类似于应用多个卷积层后应用的视觉注意机制。此外,考虑到评估的网络结构输出为隶属度概率向量,因此使用加权熵损失函数对结果进行评估:
(14)

2.4 复杂性分析
BL模型的空间复杂度为O(DD′+TT′+D′T′),所提时间注意增强BL模型空间复杂度为O(T2)。BL模型的计算复杂度包括两个环节:①矩阵乘法W1XW2,计算复杂度为O(DD′T+D′TT′);②偏置移位和非线性激活,计算复杂度为O(2D′T′)。因此,BL模型的总体计算复杂度OBL为:
OBL=O(DD′T+D′TT′+2D′T′)
(15)
所提时间注意增强BL模型具有与BL模型中相同的计算步骤以及对注意步骤的额外计算,因此总计算复杂度OBL′为:
OBL′=O(DD′T+D′TT′+2D′T′+D′T2+3D′T)
(16)
式中:D′T2和3D′T来自注意掩码A。
3 仿真与分析
3.1 数据集
仿真所用数据集为FI-2010数据集。该数据是从纳斯达克北欧证券交易所收集的不同股票中获取,收集期为2010年6月1日—6月14日,产生10个工作日的订单数据。数据集相关信息如表1所示。对于每个特征向量,FI-2010数据集包括与未来10、20、30、50、100个事件中的未来运动相对应的5个不同水平(H=10、20、30、50、100)中的中间价(平稳、增加和减少)的标签。

表1 实FI-2010数据集相关信息
3.2 实验与评估
将数据集分为训练集、验证集和测试集3部分,比例为8∶1∶1。网络训练时部分参数如表2所示。

表2 网络训练参数
3.2.1 实验过程
首先,将历史数据整合并进行插值,从而使得历史数据时间戳特征。然后,执行数据缩放操作,从而将所有数据转换为统一尺度。再次,对数据进行切片以生成数据链。最终,将生成的数据链带入所提模型,从而对未来数据进行预测。数据缩放计算公式如下:
(17)
(18)
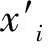
3.2.2 训练性能评估
所提模型在训练集中的性能曲线如图3所示,该模型使用损失函数和传统交叉熵损失函数进行训练,并在训练阶段进行迭代。
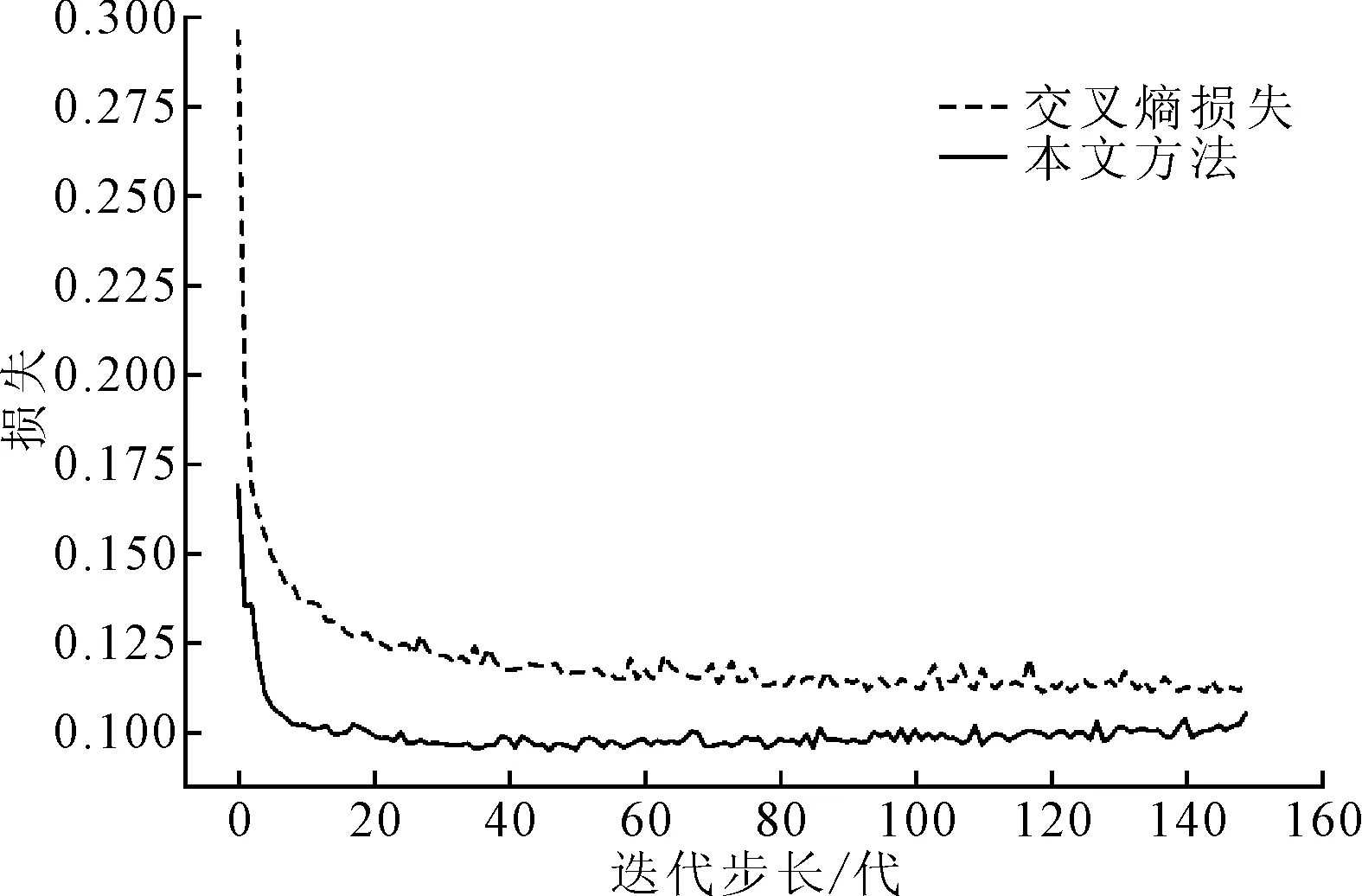
图3 不同损失函数仿真对比结果
由图3可知,损失函数训练的模型在28真步长时基本达到最优迭代,而传统交叉熵损失在95次仿真步长时才获得最优迭代。由此可见,所提的损失函数使得训练模型的收敛速度更快,且模型性能更优。
3.2.3 测试性能评估
改进方法与LSTM、GRU方法的在测试集中准确率对比结果如图4所示。可知改进方法性能有明显提升,准确率达到84.3%,而传统LSTM和GRU方法分别为82.6%和82.1%。
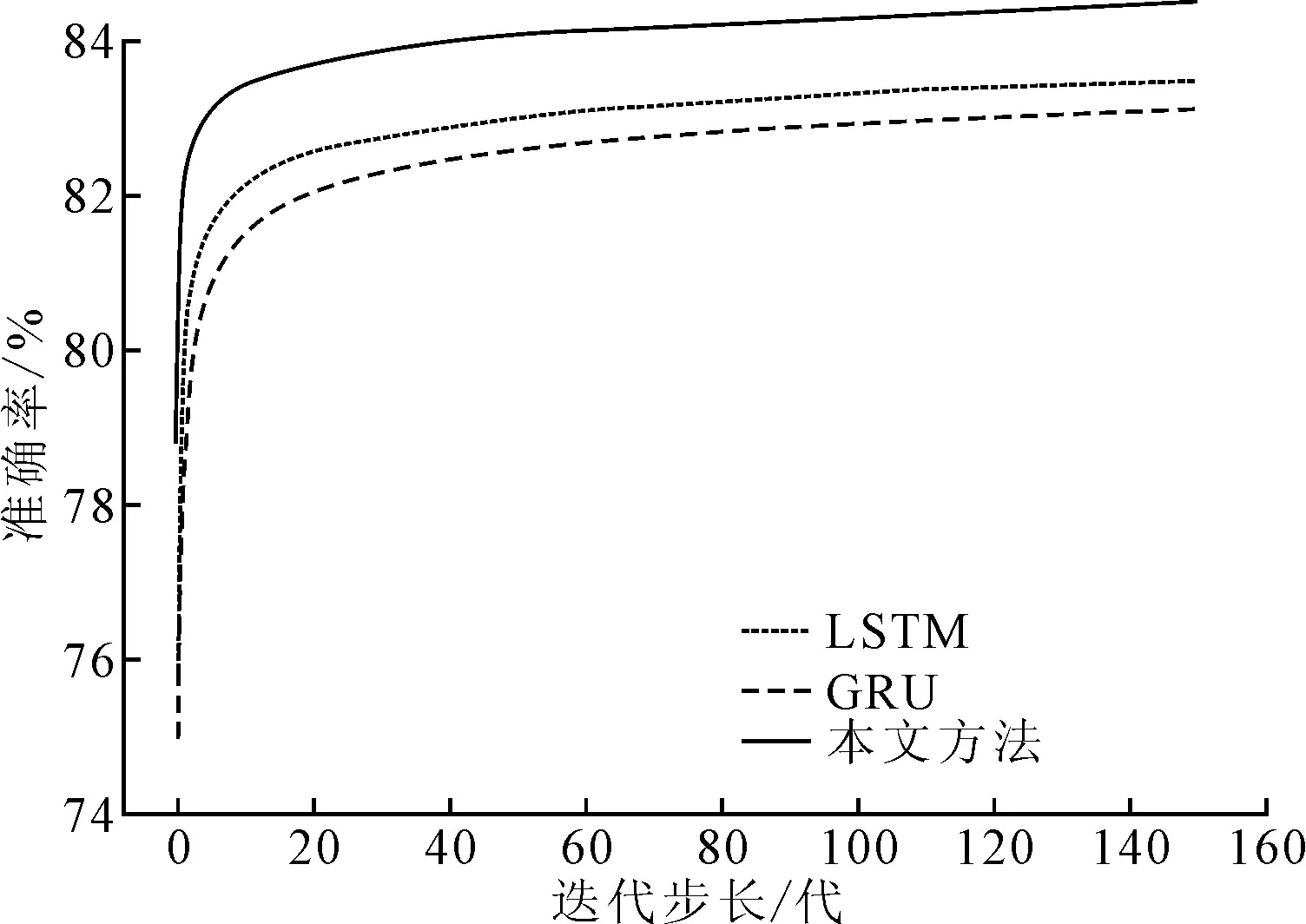
图4 不同方法准确率对比结果
4 结论
(1)基于注意机制对财务时间序列数据进行了研究与分析,提出了一种基于注意机制的深度学习模型。利用双线性层学习时间序列数据相关关系,并根据多元时间序列回归模型对结果进行预测。建立数学模型分析了股票数据序列数据特征提取以及特征学习过程,为股票时间序列数据分析及预测提供了理论参考价值。
(2)以FI-2010数据集为例,实验结果验证了所提模型能够加快时间序列数据训练效率。仿真结果进一步验证了所提模型的实践价值,对金融时间序列数据预测方面具有一定指导意义。
(3)进一步,考虑到不同金融时间序列数据可能存在显著差异,可将改进的模型作为基础模型,对其他金融数据预测时利用迁移模型并通过微调(fine-tuning)到另一个数据集。未来工作可对迁移模型进行研究,从而进一步提升模型泛化能力,拓展模型应用场景。
