基于流形学习的企业信用风险组合评价模型
2022-11-28周礼刚刘欣悦朱家明陈华友
罗 敏,周礼刚,刘欣悦,朱家明,陈华友
(1.安徽大学 数学科学学院,安徽 合肥 230601;2.安徽大学 应用数学中心,安徽 合肥 230601;3.安徽大学 互联网学院,安徽 合肥 230601)
2009年10月,中国创业板正式上市,首批28家企业开市交易,作为主板市场的重要补充,有效缓解了暂时无法在主板市场上市的中小企业、创业型企业的融资难题,市场规模迅速发展壮大。截至2021年8月4日,创业板总市值达135 510.81亿元,累计融资10 003.63亿元,上市公司数量突破1 000家。但企业大多处于创业成长期,成立时间较短,资本规模较小,业绩较不稳定,相较于大型成熟企业,抗风险能力较弱,易受政策调整、经营不善、经济下行等因素的冲击,导致资金运转失灵,进而产生信用风险。对此,金融监管部门先后推行了创业板企业退市制度、创业板注册制等改革,并不断完善相关法律法规,从政策层面上降低企业发生违约的概率。考虑到企业的财务指标等信息能够从数据层面上揭示企业的违约风险,有必要分析影响企业信用风险的诸多因素,构建科学合理的信用风险评价模型,预测企业潜在的信用风险,完善风险预警机制,为创业板企业信用风险评价提供丰富的理论依据和技术支持。
企业信用风险评价一直是国内外学者广泛关注和研究的课题[1-3],研究者通常将信用风险评价视为模式识别的分类问题,即判断企业信用风险水平属于正常或异常中。运用一定方法从企业历史数据样本中探究分类规则,并建立评价模型判别新样本。根据方法的不同,可分为单变量判别分析、多变量判别分析、机器学习等。BEAVER[4]最早使用单个财务指标分析企业信用风险水平。该方法简单易理解,但单一的财务指标不能反映企业整体的信用风险水平,利用不同指标信息得出的评价结果也可能相互矛盾。因此,在单变量判别分析的基础上扩展出了企业信用风险多变量评价模型。典型的多变量模型包括多元判别模型[5]和多元回归模型[6]。
随着现代信息技术的进步,贝叶斯分类[7]、决策树(decision tree, DT)分类[8]、支持向量机(support vector machine, SVM)分类[9]、神经网络(neural networks, NNs)[10]等非线性分类方法迅猛发展。文献[7]构建了离散型贝叶斯网络模拟贷款用户的违约概率,结果显示贝叶斯网络能够突破传统统计方法的诸多限制,分类准确率较高。TIAN等[11]采用梯形提升决策树算法,预测精度达92.19%。文献[9]在对德国公司违约概率的预测中,发现SVM分类器的预测精度显著高于Logistic模型,其增幅约为25%。涂艳等[12]基于“拍拍贷”平台的真实交易数据,构建了支持向量机、神经网络、决策树等机器学习模型,预测借款者发生违约行为的概率,结果表明,机器学习方法能有效提升预测的准确率,其中神经网络、决策树、随机森林算法的分类效果更佳。
上述方法有着各自的适用情形和限定条件,为综合不同方法的优点,分散单一模型分类错误所产生的风险,张新红等[13]将Logistic模型和RBF神经网络模型进行组合,分析我国上市公司的信用风险情况,结果表明组合评价模型优于单一模型。彭伟[14]将最优组合的思想应用到信用风险评价中,提出了基于随机森林和Logistic回归的组合评价模型,结果与文献[13]研究成果一致,组合评价模型不仅能够综合各单项模型的优势,提高评价的精度,还能降低单一模型评价错误所带来的风险。但是,已有的组合评价模型一方面是对方法进行组合,另一方面是对不同单项评价模型的结果赋予一定的权重进行最优组合。事实上,不同单项评价模型对不同企业的评价性能是“时好时坏”的,比如说,数据差异较小时贝叶斯分类效果更好,数据差异较大时BP神经网络分类效果更好,组合权重体现了该种单项评价方法的重要性程度,同时,单项评价方法在组合评价中的权系数用变权会更贴切一些,即根据单项评价方法的评价结果,对评价高的时刻赋予较大的权重。
然而,在实际企业信用风险评价问题中,影响企业信用风险的指标众多,如果不能合理选取变量,将会产生严重的多重共线性问题,从而降低分类的准确度和模型的解释性。常用的数据降维方法有主成分分析和Lasso回归方法等,但这些降维方法或丢失部分原始数据信息,或提高了数据的稀疏性,从而导致评价误差的增大,因此,笔者基于流形学习的局部线性嵌入(locally linear embedding, LLE)方法对企业财务指标数据进行降维。与传统降维方法相比,流形学习是局部线性的,利用线性重构的局部对称性质,学习非线性流形的全局结构,进而将高维数据映射到低维空间,保持数据在高维空间的几何拓扑结构。姚明海等[15]利用LLE方法对瓷片表面样本数据进行降维处理,继而利用SVM方法进行分类学习,提出一种基于局部线性嵌入的SVM增量学习方法,结果表明,该算法提高了对高维数据的运算速度以及分类的精度。王波等[16]利用局部线性嵌入算法对人脸数据的特征进行特征,并利用极限学习机算法对降维后的数据进行分类,数据表明,与利用主成分分析算法相比,LLE算法具有更高的识别速度和识别精度。
综上所述,笔者对财务指标与企业违约状况进行相关性分析,剔除不相关指标,为解决指标之间的多重共线性问题,降低冗余信息对评价结果的影响,引入局部线性嵌入的流形学习方法对财务指标数据进行降维处理,考虑到已有的企业信用风险组合评价模型在组合的过程中仅使用固定权重对单项方法进行赋权,提出一种变权组合评价模型并随机选取样本进行实验,验证模型的有效性。
1 基于流形学习与诱导有序集成的企业信用风险变权组合评价模型
首先介绍基于流形学习的局部线性嵌入(LLE)方法对财务指标数据的处理过程,分别利用贝叶斯分类、决策树分类和BP神经网络3种方法对LLE处理后的数据进行分类学习,最后,基于3种单项分类模型的结果,构建基于流形学习与诱导有序集成的企业信用风险变权组合评价模型。
1.1 基于流形学习的财务指标数据降维方法
企业财务评价指标种类繁多,这将导致收集到的数据存在一定的冗余信息,为了降低冗余信息对评价结果的影响,基于流形学习的局部线性嵌入(LLE)法[17]对财务指标数据进行降维。与传统的降维方法相比,LLE方法是局部线性的,利用线性重构的局部对称性质,学习非线性流形的全局结构,该方法能够保持样本数据的局部拓扑结构。假设有n个企业,违约情况序列记为Yi,i=1,2,…,n,其中Yi=1表示第i个企业未违约,Yi=0表示第i个企业违约,若第i个企业的财务指标数据为Xij=(Xi1,Xi2,…,Xim),则用矩阵表示为X=(xij)n×m。为将矩阵X降成d维矩阵Z=(zij)n×d,基于LLE方法的降维步骤如下:
(1)寻找各样本点的近邻点,构建邻域图。对于任意样本点Xij,计算与相邻样本点的欧式距离,确定其ε-邻域内的近邻点所构成的集合,记为Qi,将每个点与其近邻点建立加权邻域图。
(2)采用如下模型计算集合Qi中的近邻样本点对Xij进行局部线性重构的权重系数ωik:
(1)
若k∉Qi,则ωik=0。
(3)令(W)ik=ωik,由式(2)可得降维后的低维矩阵M:
M=(I-W)T(I-W)
(2)
(4)对低维矩阵M进行特征分解,即M=PΛPT,其中P为特征值所对应的特征向量,Λ为对角线元素为特征值的对角矩阵,取Λ的最小的d个特征值所对应的特征向量,令Λ*=diag(λ1,λ2,…,λd),则P*为d个最下特征值对应的特征向量矩阵。
(5)通过计算Z=P*Λ*1/2∈Rm×d,得到降维后的矩阵Z,其中,每一行代表一个样本数据的低维坐标。
根据上述步骤即可得到基于流形学习的局部线性嵌入法降维后的财务指标数据。为得到变权组合评价值,利用贝叶斯分类、决策树分类和BP神经网络3种分类方法根据财务指标降维后的数据进行分类评价。
1.2 基于贝叶斯分类的企业信用风险评价模型
朴素贝叶斯是基于先验概率的一种常用的分类学习算法,其思想是对于给定的待分类项,分别计算在该项条件下各个类别的概率,然后选择概率最大的,归为该类。
设Yi为第i个企业的违约情况,Yi的类别集合为C={0,1},Xij(i=1,2,…,n,j=1,2,…,m)为Yi第i个企业第j个财务指标数据,计算p(0|Yi)和p(1|Yi),若p(0|Yi)>p(1|Yi)则Yi=0,即Yi是违约的;反之则Yi=1,为未违约。
一般情况下,p(0|Yi)和p(1|Yi)是未知的,可根据样本集合计算各类别下不同特征的条件概率,即pj(Xij|0)和pj(Xij|1),由贝叶斯定理可知:
(3)
(4)
由于式(3)和式(4)中分母均为所有的类别,对概率计算无影响,因此只考虑分子,假设各个特征相互独立,则有式(5)和式(6)成立,从而得到p(0|Yi)和p(1|Yi),进而可得Yi的分类。
(5)
(6)
1.3 基于决策树分类的企业信用风险评价模型
决策树分类是一种有监督的分类学习算法,能够从样本数据中总结出决策规则,并且用树状图呈现分类规则,一棵决策树包含一个根结点、若干个叶结点和内部节点,从根结点到叶结点形成一条路径作为一条分类规则,最终在非叶结点上进行决策。在识别企业是否违约的实际决策问题中,首先将企业的样本数据全部纳入根结点,通过判断各指标加入后对决策结果的影响水平,即各指标的信息增益,若某一指标的信息增益越大,说明该指标对分类的作用越大。因此,可通过各指标的信息增益来对指标进行特征划分,选择出最重要的指标优先分裂。
假设企业是否违约的数据为Y=(y1,y2,…,yn),相应的概率为P=(p1,p2,…,pn),则样本Y的信息熵为:
(7)
则在每个指标属性下样本的条件熵为:
H(Y|Xi)=P(Xi)H(Y|Xi)
(8)
结合式(7)和式(8)可得第i个指标的信息增益为:
IG(Xi)=H(Y|Xi)-H(Y)
(9)
由式(9)可依次选择指标进行分列,生成一棵决策树分类,进而根据样本数据对企业的违约情况进行分类。
于是非常的热闹,比方我的母亲,她一点也不懂这行,但是她也列了席,她坐在旁边观看,连家里的厨子,女工,都停下了工作来望着我们,似乎他们不是听什么乐器,而是在看人。我们聚满了一客厅。这些乐器的声音,大概很远的邻居都可以听到。
1.4 基于BP神经网络的企业信用风险评价模型
BP神经网络[18]最早由RUMELHART等提出,是一种误差逆向传播训练的多层神经网络,由输入层、模式层和隐藏层构成,可用于分类和预测问题。它通过对训练结果与期望结果进行误差分析,不断修正模型的权值和阈值,最终得到理想结果,如图1所示。

图1 BP神经网络结构图
针对企业违约的二分类问题,假设评价企业违约情况的相关指标数据及企业是否违约的数据集为{(Xi,Yi)},i=1,2,…,n,Xi∈Rn为第i个指标数据的特征向量,Yi为第i个企业的违约情况,若违约则Yi=0;反之,Yi=1。令Xi为输入变量,Yi为输出变量,设vip(i=1,2,…,d;p=1,2,…,q)为输入层到隐藏层的连接权重,αp为第q个隐藏层单元的输出,则:
(10)
设vpj(p=1,2,…,q;j=1,2,…,q)为隐藏层到输出层的连接权重,隐藏层第p个神经元的阈值为γp,则第j个输出神经元的输入为:
(11)
式中:bp=f(αp-γp),f为激活函数,可选用Sigmod函数。
最终可得到最后输出为:Yi=f(βj-θj),θj为输出层第j个神经元的阈值。
1.5 基于诱导有序集成的企业信用风险最优变权组合评价模型
同一单项分类评价方法对不同企业的评价精度不同,不同单项评价模型由于自身特点对不同企业的评价性能也“时好时坏”。因此,可能出现某种单项分类方法对某个企业的评价精度较高而对其他企业评价精度低的情况,为克服这些缺陷,引入诱导有序加权平均(induced ordered weighted averaging,IOWA)算子,将单项分类评价方法对样本企业的评价精度由高到低排序后进行赋权,提出一种新的变权组合评价方法。
设Yi为第i个企业是否违约数据,假设有m种分类方法对其进行分类预测,令第j种分类方法对第i个企业是否违约的预测结果为Yji,称eji=Yji-Yi为第j种分类方法对第i个企业的评价误差。
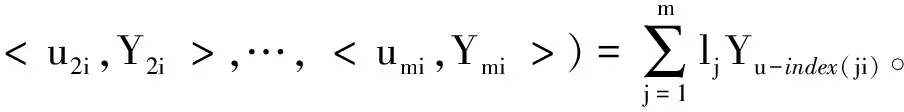
根据定义1和定义2,由第j种单项分类评价方法对第i个企业的评价值Yji及实际值Yi可以得到第j种单项分类评价方法在第i个企业的评价精度uji,以uji作为Yji的诱导值,组成一个二维数组,记为
(12)
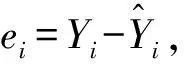
(13)
2 实例仿真与结果分析
2.1 数据来源
以深圳证券交易所的300家创业板企业为研究样本,其中21家ST类公司为信用异常样本,将这21家公司被ST前一年的数据作为训练数据。根据与ST公司所处行业相同或相近、资产规模相差控制在20%以内的原则,配比279家信用正常样本。数据来源于国泰安数据库、上市公司企业年报等。
综合创业板企业的风险特征和已有文献的研究经验,从盈利能力、短期偿债能力、长期偿债能力、发展能力及运营效率5方面初步选取21个影响企业信用水平的指标,分别为毛利率、净资产收益率、总资产净利润率、资产负债率、流动比率、速动比率、现金比率、长期资本负债率、产权比率、流动资产比率、流动负债率、净利润增长率、净资产增长率、营业收入增长率、总资产增长率、现金流量增长率、总资产周转率、流动资产周转率、存货周转率、股东权益周转率和应收账款周转率。
2.2 信用风险分类评价指标
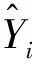
(14)
(15)
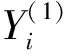
(16)
(17)
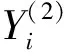
(18)
(19)
2.3 实证结果分析
利用样本数据计算企业违约情况与各指标的相关系数,结果为:0.39,0.40,0.46,-0.54,0.16,0.14,0.10,-0.31,-0.40,-0.33,0.07,0.16,0.43,0.11,0.16,0.06,0.23,0.16,-0.01,0.22,-0.01,并剔除相关性弱的指标,分别为流动比率、速动比率、现金比率、流动负债率、净利润增长率、营业收入增长率、总资产增长率、现金流量增长率、流动资产周转率、存货周转率和应收账款周转率。考虑到剩余指标之间可能存在多重共线性问题,采用基于流形学习的局部线性嵌入法对指标进行约简。从300家创业板企业中随机选取2组样本,每组样本中,包含270家训练样本及30家测试样本。再利用贝叶斯分类模型、决策树模型、BP神经网络模型和最优组合模型对2组样本进行分类评价。
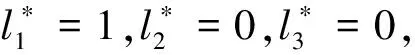

图2 随机样本1模型测试结果
由式(14)~式(19)可得各模型的分类准确率,结果如表1所示,可知在训练样本和测试样本中,组合分类评价模型的分类精度在4个模型中均为最高。在测试样本中,组合模型对总体识别的正确率为96.67%,高于3种单项分类方法;对异常样本的识别正确率为83.33%,与决策树方法相同,远高于贝叶斯方法和BP神经网络方法;对正常样本的识别正确率为100%,高于3种单项分类方法。
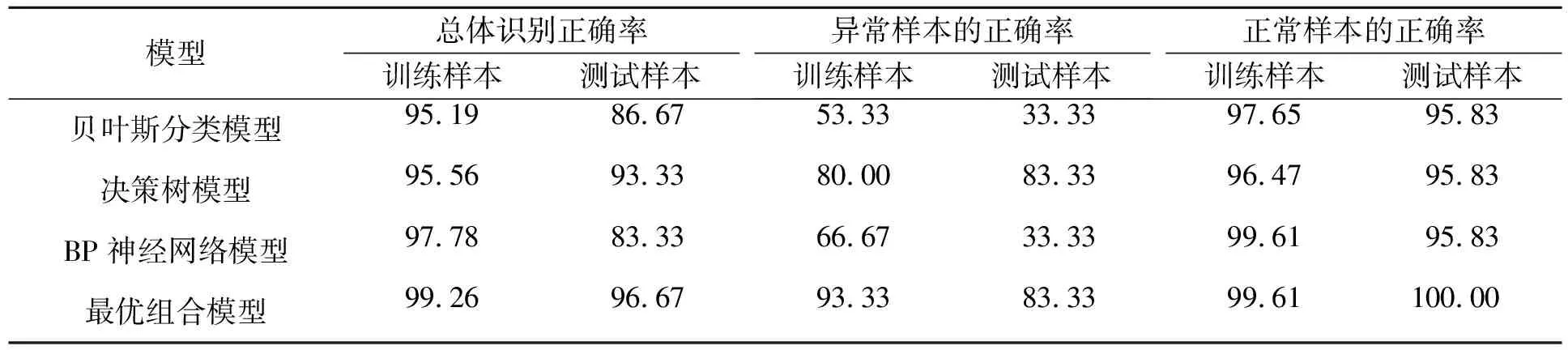
表1 创业板企业信用风险评价方法识别精度比较(随机样本1) %
为验证模型的稳定性,随机选取第2个样本,进行再次验证,结果如图3所示,可知组合分类模型的预测准确率高于3种单项分类模型。
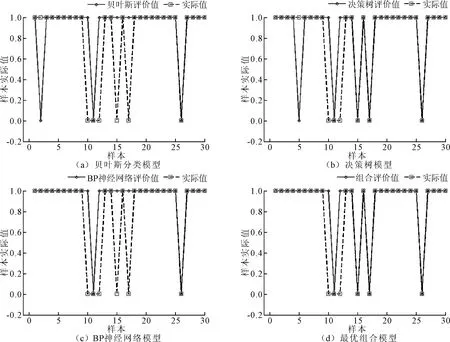
图3 随机样本2模型测试结果
由式(14)~式(19)可得各模型的分类准确率,结果如表2所示,可知在训练样本和测试样本中,组合评价模型的分类精度在4个模型中仍为最高,与随机样本1的结论保持一致。在测试样本中,组合模型对总体识别的正确率为93.33%,高于3种单项分类方法;对异常样本识别的正确率为66.67%,与决策树方法相同,远高于其他两种方法;对正常样本识别的正确率为100%,高于3种单项分类方法。综上,相较于正常样本的识别问题,组合模型能显著改善部分单项方法对异常样本识别正确率较低的问题,具有现实意义和应用价值,提出的基于诱导有序集成的变权组合分类评价模型是合理有效的。

表2 创业板企业信用风险评价方法识别精度比较(随机样本2) %
3 结论
(1)选取了21个影响企业信用的评价指标,基于300家创业板企业的样本数据,首先计算各评价指标与企业违约情况的相关性,并剔除了相关性弱的指标;其次利用基于流形学习的LLE方法对指标进行约简,以消除冗余信息对模型的影响;继而利用贝叶斯分类、决策树模型以及BP神经网络3种分类模型对企业是否违约进行分类评价。结果表明3种分类方法对不同企业的评价精度“忽高忽低”,为融合不同方法所提供的有效信息,构建基于诱导有序集成的变权组合评价模型,并随机选择两组训练样本和测试样本,结果表明,组合评价模型能有效提高分类精度,并分散由单一模型分类错误所带来的风险。这说明笔者提出的模型在解决企业信用评价分类问题时效果显著。
(2)在未来的研究中,一方面,考虑继续挖掘数据特征,利用深度学习方法进行评价。另一方面,考虑将文本信息等非结构化数据与财务数据相结合,构建基于结构化与非结构化融合的组合评价模型,进一步提高模型的分类精度及适用性。
