我国石油消耗量的影响因素分析及预测
2022-11-28郄慧娟张权王珂
郄慧娟,张权,王珂
(齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006)
国外从石油价格、消耗量及石油对经济的影响等方面研究。UCHE[1]运用ARDL 技术对一些欧洲的国家在石油价格、收入变化和汇率方面的非对称性进行了评估。WANG 等[2]通过分析美国石油消费的模拟值与真实值之间的差异,发现疫情对美国石油消费的影响在2020 年4~5 月和2021 年1~2 月较为明显。ZHU 等[3]通过GARCHSK-mix Copula-CoVaR-Network 方法探究了疫情期间原油、美国和中国股市之间的多维风险溢出。国内对能源的研究大致可分为分解法和构建STIRPAT 模型和其他方法,王丽丽等[4]在关于碳排放的问题上,利用结构分解法进行研究,陈庆等[5]构建STIRPAT 来研究对武汉市的环境影响因素。对于能源的预测,王婷[6]对中俄东线天然气管道地质灾害进行了安全风险评价分析,WU 等[7]采用参数优化及分数累积的方法对能源进行了预测,谢乃明等[8]利用二次规划灰色模型的马尔可夫方法,对能源的消耗及生产进行预测,马新[9]利用时滞多项式的灰色预测模型预测我国天然气的消费量,丁松等[10]用非线性的自适应灰色系统对我国天然气的需求量进行了预测。
本文就石油的影响因素和石油消耗量的预测进行研究,对石油消耗量影响因素进行因子分析,用灰色模型和灰色马尔可夫组合模型对石油消耗量进行预测,并用平均相对误差和模型精度来对比预测效果。最后,根据上文的分析得出结论,为我国未来石油资源的发展利用提出合理的建议。
1 相关理论
1.1 因子分析
因子分析是统计学的一种典型方法,在所有变量中提取出共性因素,根据各个变量之间隐藏的某种相关性,推断其中是否存在某种共性因子可以代表本质相同的因子,可以有效地减少变量的数量,同时尽最大可能保存原有信息。
因子分析的数学模型:设有p个可观测的指标(标准化后):

因子模型记为X=Ap×mF+ε,其中,X= (X1,X2, …,Xp)′是可观测的随机向量F= (F1,F2, …,Fm)′是不可观测的变量,ε= (ε1,ε2, …,εp)′与F不相关。aij是第i个变量与第j个公共因子的相关系数aij=ρij= cov(X i,Fj)。
因子分析的指标体系构建需要满足以下原则:
(1)科学性。构建一个合适的指标体系首先需要满足科学性,选取的指标要有科学依据支撑,并且满足实践意义,理论及实践都满足科学性,才能够到达科学性的要求。
(2)系统性。石油的影响因素是一个复杂的系统,选取影响指标时需充分考虑到系统性,将各个指标的系统性与科学性相结合,构建出完整的指标体系。
(3)重点性。选取的指标应具有侧重点,石油的消耗量多余各种行业的发展以及经济因素有关,因此指标选取时的侧重点要有所倾斜。
(4)可操作性。选取的指标,应尽量使数据来自于相关部门的专业数据,更具有说服性和专业性,分析结果更具可靠性。
1.2 灰色模型和灰色-马尔可夫模型
背景值优化的灰色模型能够反映预测的整体趋势,但不能反映出数据的波动性,马尔科夫链恰好弥补了灰色模型的缺点,因此背景值优化的灰色马尔可夫模型可以降低模型的预测误差,提高预测精度。
1.2.1 背景值优化的灰色模型
灰色预测通过鉴别系统因素间的发展趋势的关联程度,对原始数据生成有较强规律性的数据序列,然后建立相应的微分方程模型预测事物未来的发展趋势。
(1)建模过程。为了保证GM(1,1)模型的可行性,需要对已知的数据进行级比检验。设原始数据的序列为

其中,x(0)(k) > 0,k= 1,2, … ,n。
①数列的级比:

②对X(0)累计相加,生成1 -AGO序列:
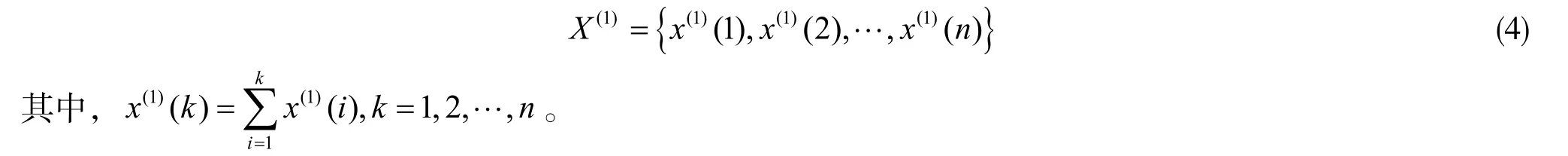
③由序列X(1)建立GM(1,1)模型的白化方程为

④GM(1,1)模型的灰色微分方程为

优化的背景值序列[11]为

其中,a和b为模型的待估参数,
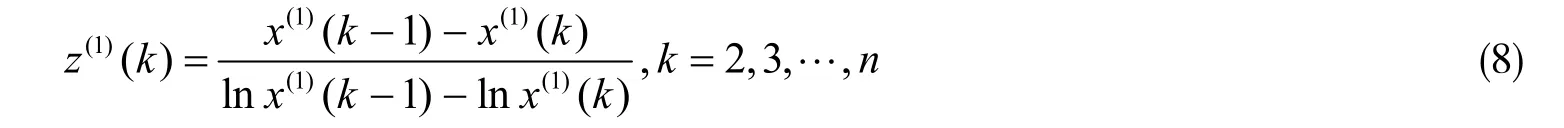
⑤通过计算一阶线性微分方程的解,可得GM(1,1)的模型的响应函数为
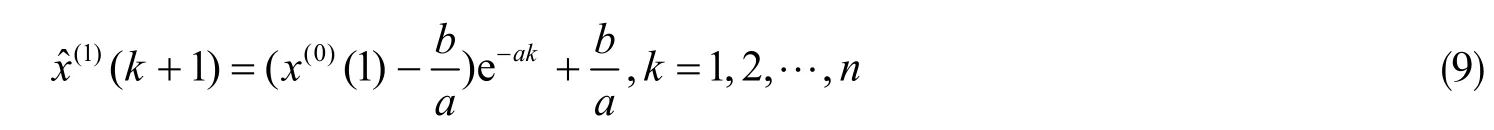
其中,xˆ(0)(k+ 1) =xˆ(1)(k+ 1) -xˆ(1)(k),k= 1,2, … ,n。
(2)精度检验。在实际问题中,需要通过检验去判定灰色模型的合理性和适用性。模型的精度越高,预测的数据越准确。灰色模型可通过相对误差、均方差比值和关联度3 种方法来判断模型的精度。
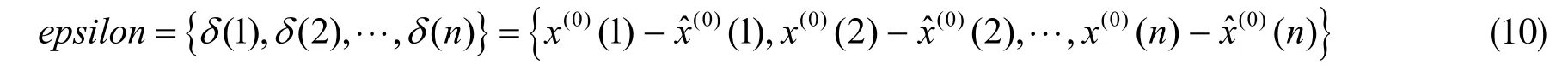
残差序列为相对误差序列为:
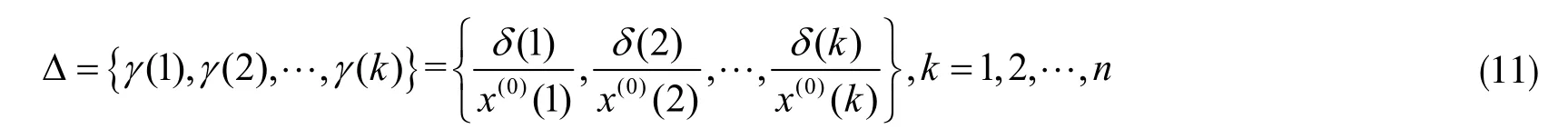

1.2.2 灰色-马尔可夫模型
灰色马尔可夫模型利用马尔可夫确定状态的转移概率及概率矩阵,修正灰色模型的相对误差,使模型的精度更高,从而使预测效果更好。
第一步:划分状态。以灰色预测模型中优化后的背景值序列和原始非负序列之间的相对误差序列作为预测模型的观测数据,将相对误差进行排序,并划分为r个不同的状态Ei= (E1,E2, … ,Er),任意状态表示为Ei= [ai,bi],i= 1,2, … ,r,其中ai,bi为适当的常数。

第三步:状态转移概率矩阵。根据相对误差序列 Δ= {γ( 1),γ( 2), … ,γ(k)},可知处于Ei状态的观测值有Mi个,因此,从状态Ei到Ej的一步转移概率pij为

因为不知道最后一个观测值的状态转移情况,所以不参加计算,即 ΣMij=n-1。
一步~四步状态转移概率矩阵分别为Pij,Fi j=Pij*Pij,Gi j=Fi j*Pij和H ij=Gi j*Pij。
第四步:马氏检验。选定置信水平α,如果χ2>((n- 1)2),则该模型通过检验,可用于实际预测。
第五步:建立预测状态转移矩阵。根据状态的个数选择距预测值最近的r个观测值,建立新的动态预测状态转移矩阵Li j,i=1,2, …,r,j=1,2, … ,r,计算矩阵Lij的各列之和,最大值表示预测值未来状态转移的最大可能性。
第六步:预测。通过马尔可夫链的修正,可得灰色预测区间x~(0)(k),一般取预测区间的中间值作预测值,即:
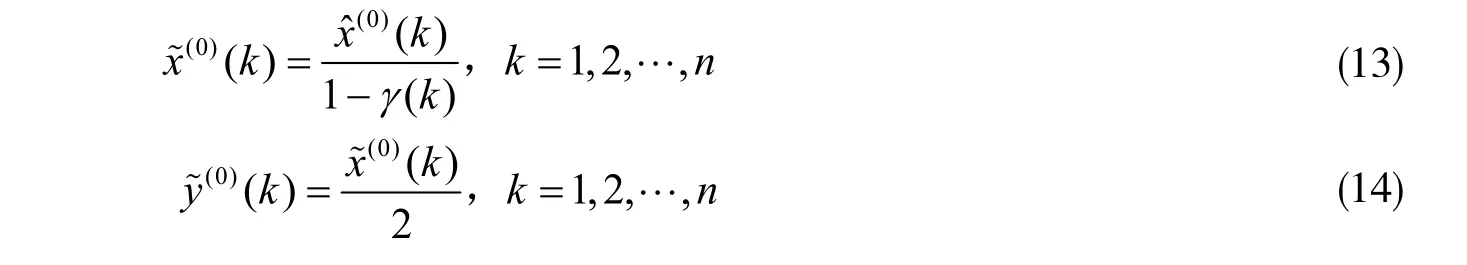
2 实证分析
本文数据来源于RESSET 数据库,选取1994~2021 年石油的相关数据,用SPSS26 对石油消耗量的影响因素进行因子分析。再利用MATLAB 和R 软件对1980~2019 年石油消耗量的数据进行模拟,2019~2021 年的数据验证模型预测的精确度,从而预测2022 年到2024 年石油的消耗量。具体指标[12]如表1 所示。
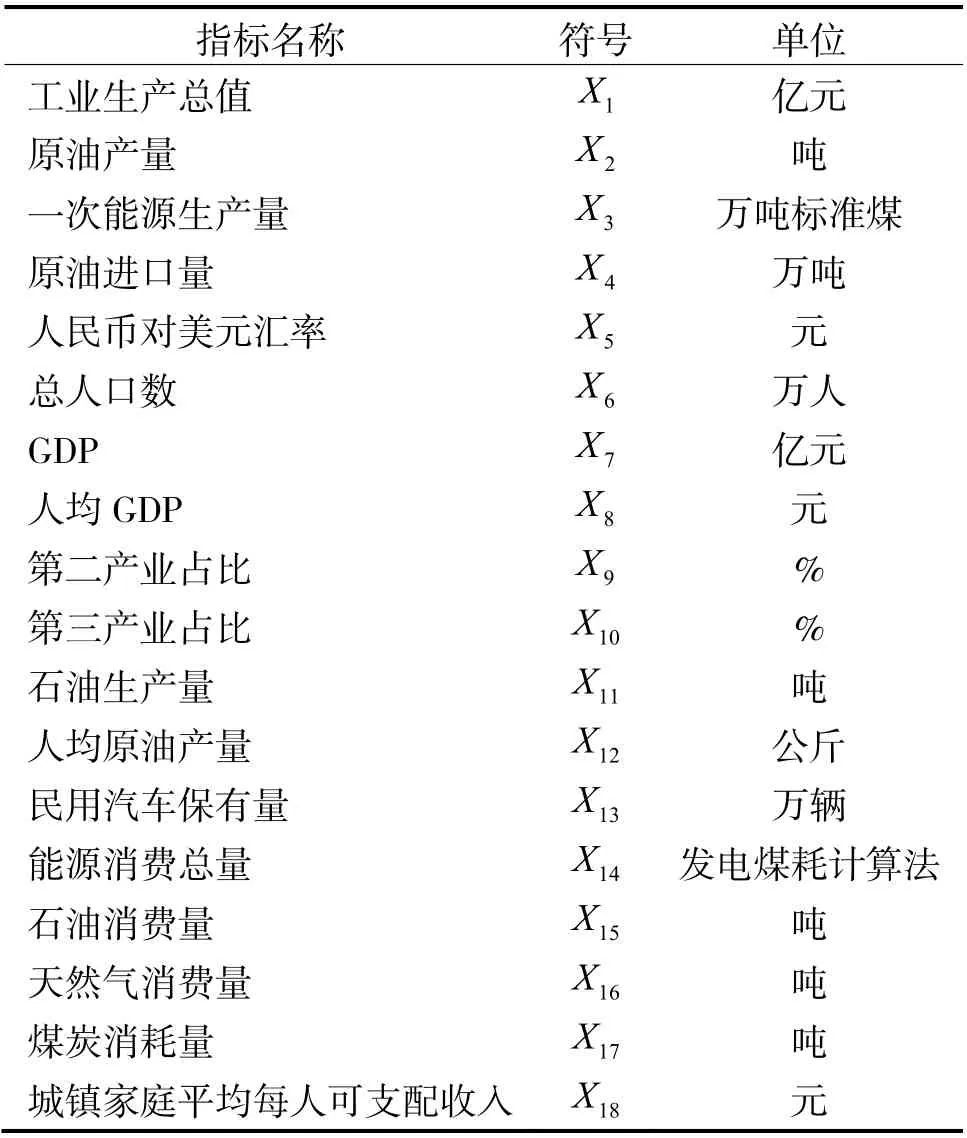
表1 指标名称、符号及单位
2.1 石油消耗量的影响因素
将构建的18 个指标的数据集导入SPSS,利用主成分分析法提取因子。主要步骤如下:
(1)用巴特利特球形检验和KMO 检验判断是否可以进行因子分析。
表2 巴特利特球度检验统计量为2 231.049,概率P值近似为零,若显著性水平为0.05,则应拒绝相关系数矩阵与单位矩阵无显著差异的假设,同时,KMO 值为0.832,根据Kaiser 给出的KMO 度量标准可知,原始变量适合进行因子分析。

表2 KMO 和Bartlett 的检验
(2)提取公共因子。主成分分析通过坐标变换能够为因子分析提供初始解,将原有的18 个相关变量做线性组合,转换成一组不相关的变量。通过SPSS 得到如表3。
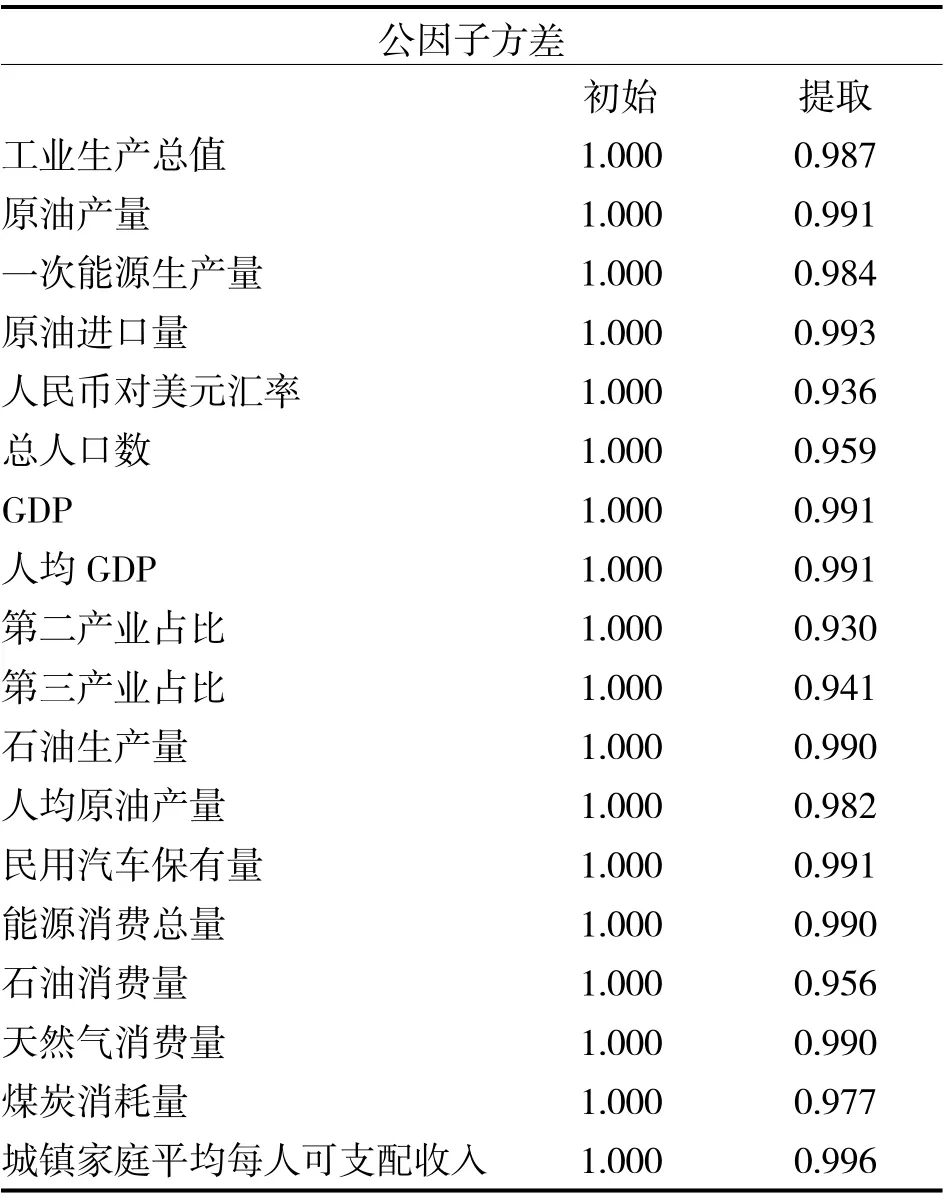
表3 因子分析中的变量共同度
由表3 可以看出,经过因子分析,对原始变量的信息提取量均大于50%,因此表明该因子分析得到的因子可以涵盖原始信息。
由表4 和图1,可知18 个变量总方差解释在提取两个因子时贡献率达到97.643%,共形成了2 个因子,经过旋转后,第一成分的占比为58.645%,第二成分的占比为38.997%。可见,通过主成分提取的前两个因子已经可以概括原问题中的大部分信息,所以,本文提取这两个因子合适(表5)。

表4 总方差解释
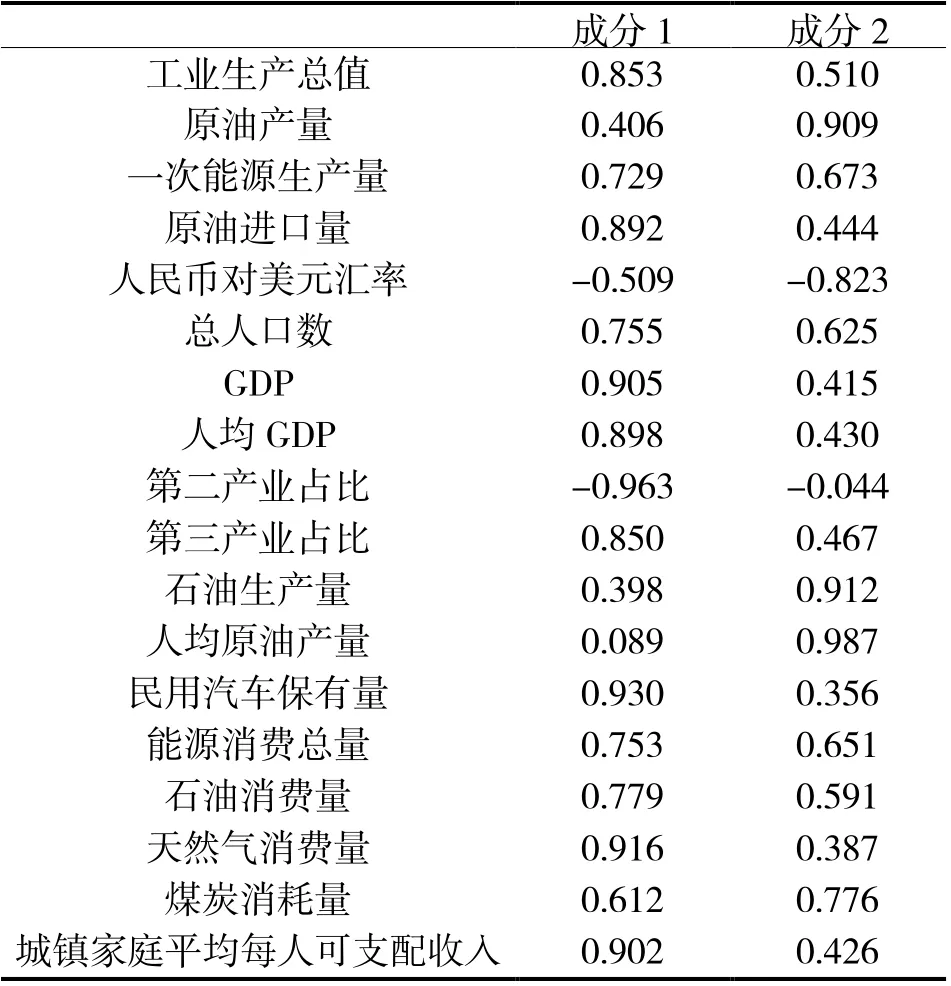
表5 旋转后的成分矩阵
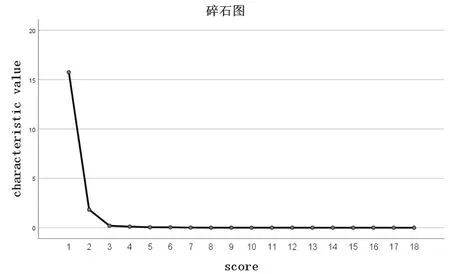
图1 碎石图
用回归法估计因子得分系数,并通过软件输出,得到因子得分系数矩阵,见表6。根据表6,可以得到因子得分函数:

表6 成分得分系数矩阵表

根据各个公因子方差贡献率,构造我国石油消耗量的综合评价模型为
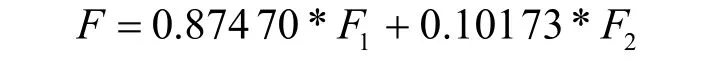
(3)结果分析。因子分析结果显示提取为两个主成分,分别命名为经济因子和社会因子,其中经济因子包括工业生产总值、原油产量、一次能源生产量、原油进口量、总人口数、GDP、人均GDP、第三产业占比、石油生产量、人均原油产量、民用汽车保有量、能源消费总量、石油消费量、天然气消费量、煤炭消耗量、城镇家庭平均每人可支配收入,社会因子包括人民币兑美元汇率和第二产业占比。其中经济因子占比87.470%,社会因子占比10.173%。
2.2 石油消耗量的预测
2.2.1 灰色预测
(1)1980~2018 年的石油消耗量的原始数据为
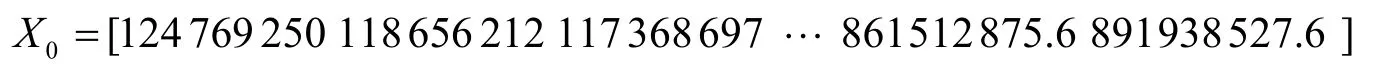
通过级比检验,可知可容覆盖区间为λ(k) = (0.9512,1.0513),原数据未通过检验,因此,做平移变换可得,C=936543613,级比序列

可进行GM(1,1)建模和预测。对Y(0)累积相加,生成AGO 序列X(1):
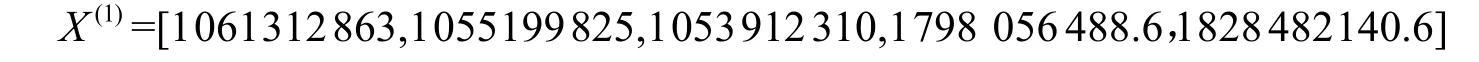
(2)用改进的背景值代替紧邻均值构造的背景值序列为


GM(1,1)的预测公式为

1980~2021 年中国石油消耗量的实际值与预测值的变化如图2。
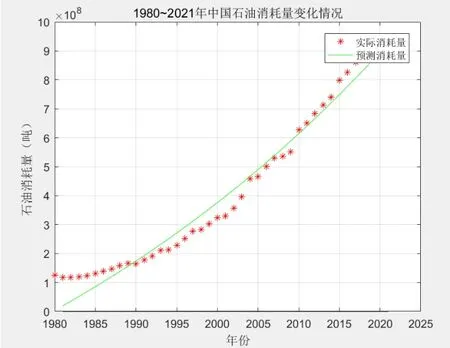
图2 1980~2021年中国石油消耗量变化情况
根据模型检验公式可得:
平均相对误差:err= 0.1572;精度:1 -=84.27%;相对关联度:r1= 0.617 8;均方差比值及小误差概率:C1= 0.174 8,P= 1。
2.2.2 灰色马尔可夫
根据均值-标准差法可将相对误差序列划分为4 个状态,即

由状态i转移到状态j的频数矩阵为一步、两步、三步和四步转移矩阵分别为


边际概率:P.j= ( 0.1627907 0.1860465 0.2790698 0.1627907)。
用2019~2021 年的数据验证模型准确度,2019 年的状态转移预测如表7。
根据表7 可知,处于E2状态的概率最大为2.109,因此,2019 年石油消耗量相对误差的预测值状态的最大概率为 2E。同理,可计算2020 年和2021 年石油消耗量的相对误差的预测值状态的最大概率也为E2。
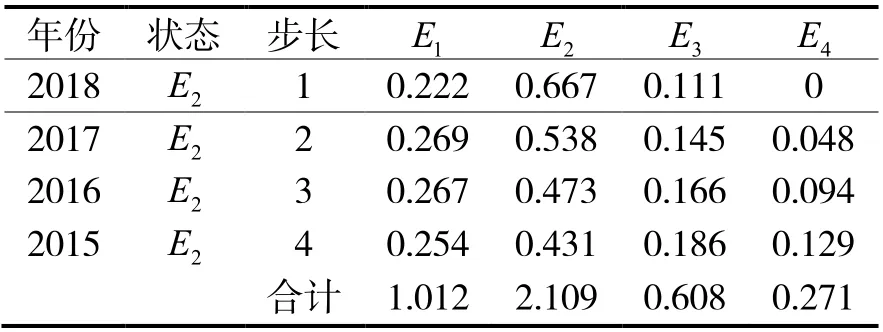
表7 2019 年石油消耗量概率预测表
通过以上数据分析,状态1 到4 出现的概率分别为:0.205 128 2, 0.256 410 3, 0.282 051 3, 0.256 410 3。因此,2022 年出现状态3 的概率最大,其消耗量的区间为(757 901 685, 991 688 497)。
根据式(13)相对误差序列所处的状态及预测,可得表8。将灰色预测区间的中间值作为马尔可夫链修正的灰色模型的预测值,部分预测结果及模拟情况如图3 所示。

表8 1980~2019 年部分预测结果
根据模型的检验公式,灰色马尔可夫组合模型的平均相对误差为0.098 481 672,模型精度为90.15%。
通过图2 和图3 及以上两个模型的预测,可知灰色马尔可夫组合模型的平均相对误差更小,模型的精度更高。因此,灰色马尔可夫的预测效果优于背景值优化的灰色模型。

图3 1980~2021 年中国石油实际及预测消耗量
3 结论
通过因子分析可知,经济因子对石油消耗量的贡献率较大,影响较深,社会因子贡献率相对于经济因子贡献率较低,因此主要对经济因子所带来的影响提出相应的对策。背景值优化的灰色模型和灰色马尔可夫模型进行预测的结果表明,灰色马尔可夫模型的预测效果更好,2022 年石油消耗量将达到757 901 685~991 688 497 t。
根据上文的分析提出以下建议:
(1)加大开采力度。在现今的世界大背景下,石油消耗量不断上升且我国的现有石油资源储量相对丰富,可以适度的加大开采。
(2)调整能源结构。国家可以开发相应的环境清洁技术,以减少煤炭带来的空气污染,另外,水、风和太阳能资源也可以缓解石油供需矛盾。
(3)提高利用率。新技术、新能源的开发与利用都需要花费大量的时间,因此对石油生产技术、利用技术进行改进,不仅可以提高石油的利用率,还可以促进经济的发展。
