水工钢筋混凝土柱塑性铰区抗剪承载力计算

2022-11-28李梦蝶孙治国吴泽斌

工程科学与技术 2022年6期

马颖，李梦蝶，孙治国，吴泽斌

(1.华北水利水电大学水利学院，河南郑州 450046；2.防灾科技学院中国地震局建筑物破坏机理与防御重点实验室，河北三河 065201；3.河南省水利勘测设计研究有限公司许昌分公司，河南许昌 461000)

钢筋混凝土（reinforced concrete，RC）柱作为水电站厂房、渡槽等水工建筑物的主要竖向承重构件，承载着整个结构的竖向荷载和由地震引起的水平荷载。因此，地震作用下RC柱极易受到损伤[1]。在地震作用下，RC柱受剪跨比、轴压比及钢筋配置等因素的影响，其破坏模式通常包括：弯曲破坏（flexure）、弯剪破坏（flexural-shear）和剪切破坏（shear）。RC柱地震破坏模式的判别可参考文献[2–4]。其中，弯曲破坏过程中抗剪需求始终小于抗剪承载力，RC柱具有较好的转动能力和延性；剪切破坏主要是剪力起控制作用，抗剪需求高于抗剪承载力时发生脆性剪切破坏，在水工结构的抗震设计中应该予以避免；弯剪破坏介于弯曲破坏和剪切破坏之间，RC柱的纵向钢筋首先屈服形成塑性铰，随后抗剪承载力随着变形的增大逐渐下降，当抗剪需求大于剩余抗剪承载力时，发生弯剪破坏，设计中也要尽量避免[5–6]。由此可见，RC柱抗剪承载力的计算对于其抗震设计及安全评估具有重要意义[7–8]。目前，中国水利行业《水工混凝土结构设计规范》（SL 191—2008）[9]（简称水利“08规范”）与中国电力行业《水工混凝土结构设计规范》（DL/T 5057—2009）[10]（简称电力“09规范”）关于RC柱抗剪承载力的计算是基于剪切破坏柱试验数据建立的半经验公式。为验证规范中的公式是否适用于弯剪破坏柱塑性铰区的抗剪承载力计算，以弯剪破坏柱为研究对象，研究水工规范中抗剪承载力计算公式是否符合弯剪破坏RC柱塑性铰区抗剪承载力的保证率要求。

近年来，很多学者对RC柱抗剪承载力计算模型进行了研究[11–12]，但部分研究者仅对国内外设计规范RC柱抗剪承载力计算公式的可靠性进行了对比；一些研究者对规范中公式的计算结果与试验结果进行了比较，并在此基础上建立了修正模型或计算模型。孙治国等[13]将高强箍筋高强混凝土柱抗剪承载力试验结果与美国《混凝土结构设计规范》（ACI 318—05）[14]和中国《混凝土结构设计规范》（GB 50010—2010）[15]的抗剪承载力计算值进行了对比，认为两种规范在计算高强箍筋高强混凝土柱抗剪承载力时均存在不安全。余波等[16]针对剪切破坏的RC柱，将国内外规范（美国《结构混凝土建筑规范要求》（ACI 318—11）[17]、中国《混凝土结构设计规范》（GB 50010—2010）[15]、水利“08规范”[9]和电力“09规范”[10]等）中抗剪承载力模型的计算结果与其改进的抗剪承载力分析模型的计算结果进行对比发现：改进的模型有效克服了传统模型无法考虑轴压比影响和需要引入经验位移延性修正系数等缺陷；中国《混凝土结构设计规范》（GB 50010—2010）[15]、水利“08规范”[9]和电力“09规范”[10]抗剪承载力公式计算值较试验值都偏低，离散性大。仇建磊[18]结合了截面受力平衡及变形协调等因素建立了钢筋混凝土柱抗剪承载力计算式，并将其建立的计算式与美国《加州桥梁抗震设计规范》（简称Caltrans规范2013）[19]及已有研究中的抗剪承载力公式进行了对比表明：其建立的计算式适用于柱构件抗剪承载力计算分析；而Caltrans规范 2013[19]形式较复杂，限制条件较多，计算准确性较差。甘丹等[20]收集试验数据，基于美国《混凝土结构设计规范》（ACI 318—14[21]）和中国《混凝土结构设计规范》（GB 50010—2010）[15]，验证现有的将钢管完全等效为箍筋的抗剪承载力计算方法的适用性，结果表明，该计算方法在方钢管宽厚比小于80或其截面边长较大时会过高估计构件的抗剪承载力；因此，针对构件受力特点，建立了基于该方法的抗剪承载力简化力学模型，且其建立的模型与《混凝土结构设计规范》（GB 50010—2010）[15]中的计算公式在形式上统一。综上可知，多数RC柱抗剪承载力修正或计算模型是基于国外规范（美国规范、加拿大规范、日本规范、欧洲规范等）抗剪承载力计算公式或国内建筑行业混凝土设计规范抗剪承载力计算公式进行的，没有基于水工设计规范中的计算公式建立修正模型，且较少关注RC柱塑性铰区的抗剪承载力计算情况，而RC柱的抗剪承载力对水工建筑物的整体安全非常重要，故有必要基于水利“08规范”和电力“09规范”研究RC柱塑性铰区抗剪承载力计算。

本文以弯剪破坏RC柱为研究对象，借助美国太平洋地震工程研究中心（Pacific Earthquake Engineering Research Center，PEER）结构抗震性能试验数据库中弯剪破坏RC柱的拟静力试验数据（矩形截面19根，圆形截面19根），采用水利“08规范”和电力“09规范”计算RC柱塑性铰区的抗剪承载力，评价水利“08规范”和电力“09规范”抗剪承载力计算公式的保证率，并对计算公式进行修正，建立RC柱塑性铰区抗剪承载力计算式，同时验证修正后计算式的保证率。

1 RC柱抗剪承载力公式

当前，RC柱的抗剪承载力Vu通常采用式（1）进行计算：

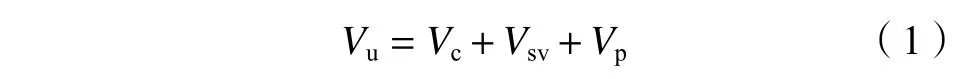
式中，Vc为混凝土的抗剪承载力，Vsv为横向钢筋（箍筋）的抗剪承载力，Vp为轴向压力产生的抗剪承载力。

水利“08规范”[9]中RC柱抗剪承载力Vu计算公式为：

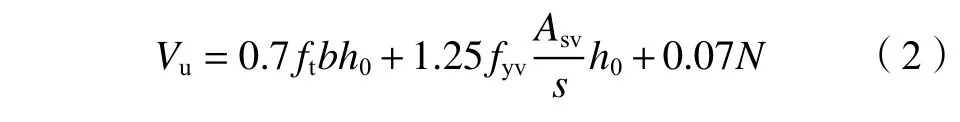
式中：ft为混凝土轴心抗拉强度，可根据混凝土轴心抗压强度（即棱柱体抗压强度）fc进行换算，即ft=0.23(fc/0.76)2/3；b为截面宽度；h0为截面有效高度，h0=h–a，h为截面高度，a为纵向钢筋合力点至截面边缘的距离；fyv为箍筋屈服强度；Asv为同一截面内箍筋各肢全部截面面积；s为箍筋间距；N为轴向压力，当N大于0.3fcA时，N取0.3fcA，A为柱的全截面面积。

电力“09规范”[10]中RC柱抗剪承载力计算公式为：

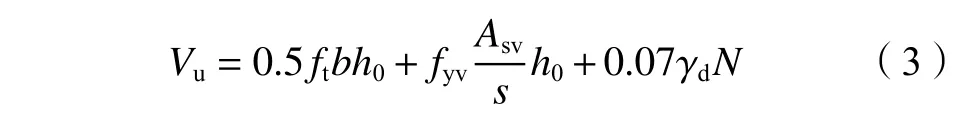
式中：γd为结构系数，材料为钢筋混凝土受压构件时，取值为1.2；箍筋屈服强度fyv取值不应大于360 N/mm2；当N大于(0.3fcA)时，N取(0.3fcA)；其他参数含义与式（2）相同。式（2）和（3）均未考虑配置弯起钢筋的情况。

由于水利“08规范”[9]和电力“09规范”[10]的RC柱抗剪承载力计算公式都只考虑矩形截面、“T”形截面及“I”形截面，并未考虑圆形截面，计算圆形截面RC柱抗剪承载力时需要进行换算（b=1.76r，h0=1.6r，其中，r为圆形截面半径）[9–10]。

由式（2）和（3）可知，水利“08规范”[9]和电力“09规范”[10]的抗剪承载力计算公式有共同点和不同点。共同点是，两者都考虑到轴向压力、截面尺寸、箍筋面积和间距、箍筋屈服强度及混凝土轴心抗压、抗拉强度的影响。不同点是：水利“08规范”[9]和电力“09规范”[10]柱相比，1）混凝土项前的系数从0.7变为0.5；2）箍筋项前的系数从1.25变为1.00；3）轴力项前的系数从0.07N变为0.07γdN。

2 弯剪破坏RC柱的试验数据

PEER结构抗震性能试验数据库是美国太平洋地震工程研究中心收集整理的试验数据，截至2004年已收录了274根矩形箍筋RC柱和160根螺旋箍筋RC柱的低周反复试验数据，由美国国家科学基金会资助，为研究人员评估研究钢筋混凝土柱的抗震性能提供了数据。

为评价水利“08规范”[9]和电力“09规范”[10]的抗剪承载力公式对RC柱塑性铰区抗剪承载力的保证率，从美国PEER结构抗震性能试验数据库中收集发生弯剪破坏的矩形截面RC柱19根和圆形截面RC柱（螺旋配箍）19根，各试件基本参数及抗剪承载力试验值见表1和2，其中，混凝土圆柱体抗压强度可根据fc=0.76/0.8（fc为混凝土轴心抗压强度）进行换算。

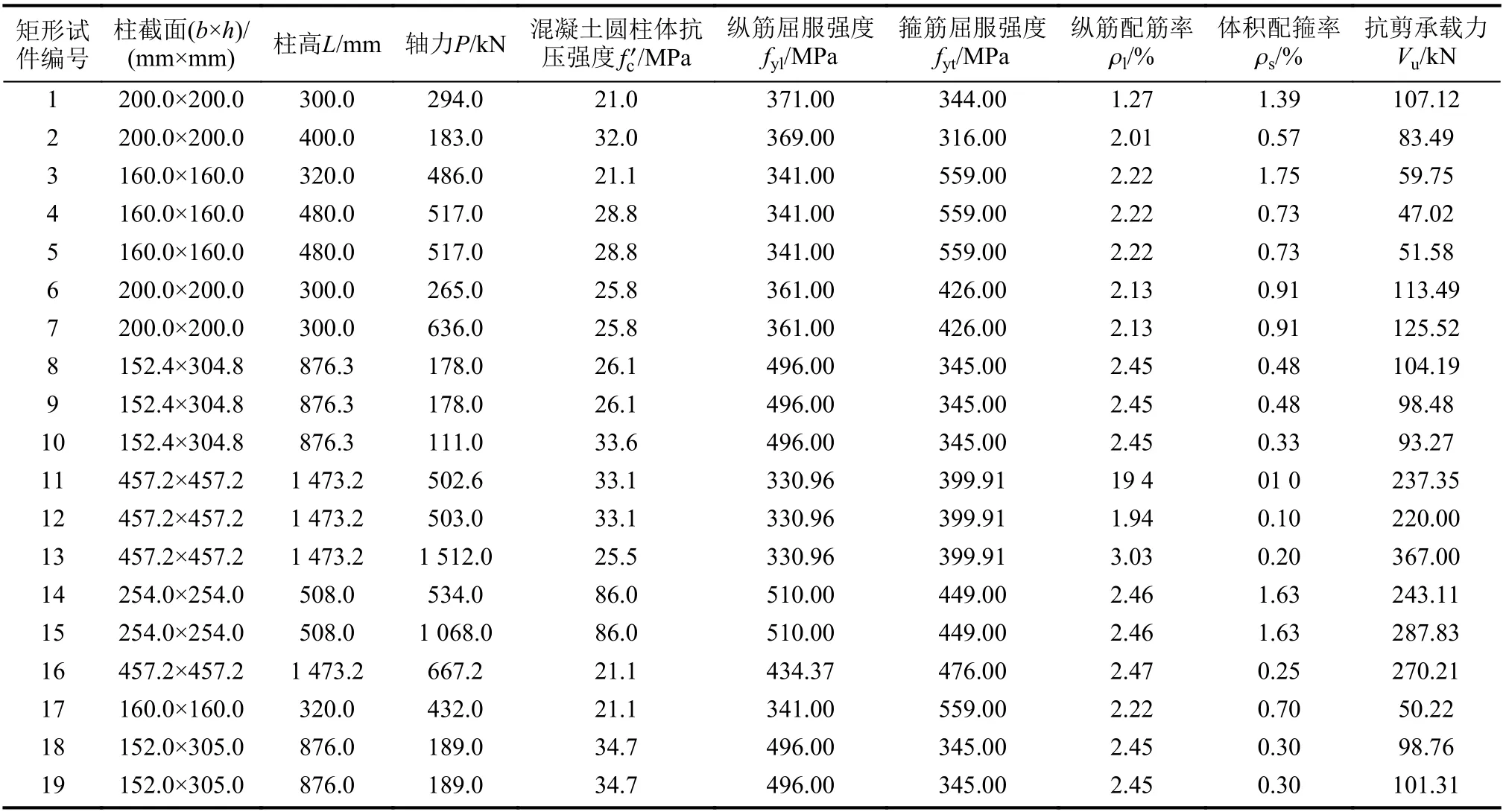
表1 矩形试件的基本参数及抗剪承载力试验值Tab.1 Basic parameters and shear capacity test values of rectangular specimens

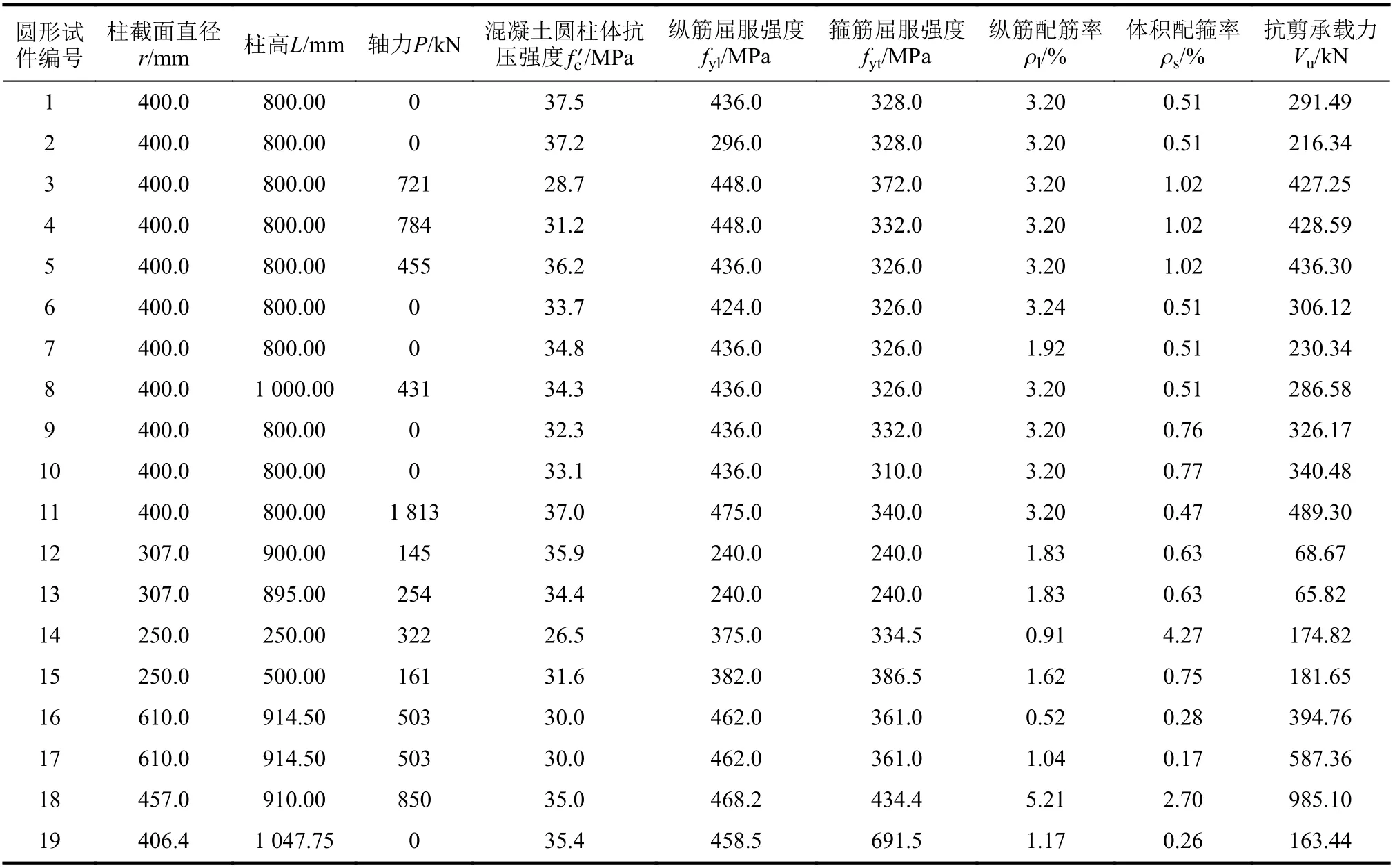
表2 圆形试件的基本参数及抗剪承载力试验值Tab.2 Basic parameters and shear capacity test values of circular specimens

3 RC柱抗剪承载力公式的分析

针对矩形截面和圆形截面，分别采用式（2）和（3）计算弯剪破坏RC柱塑性铰区的抗剪承载力，计算值和试验值，对比如图1所示。将计算值等于试验值（1∶1）作为分界线，当规范抗剪承载力公式计算值小于抗剪承载力试验值时（分界线以下，视为安全范围），表示该规范的RC柱抗剪承载力计算公式具有一定的可靠性；当规范抗剪承载力公式计算值大于试验值时（分界线以上，视为危险范围），表示在未达到抗剪承载力时柱试件就已经发生弯剪破坏。

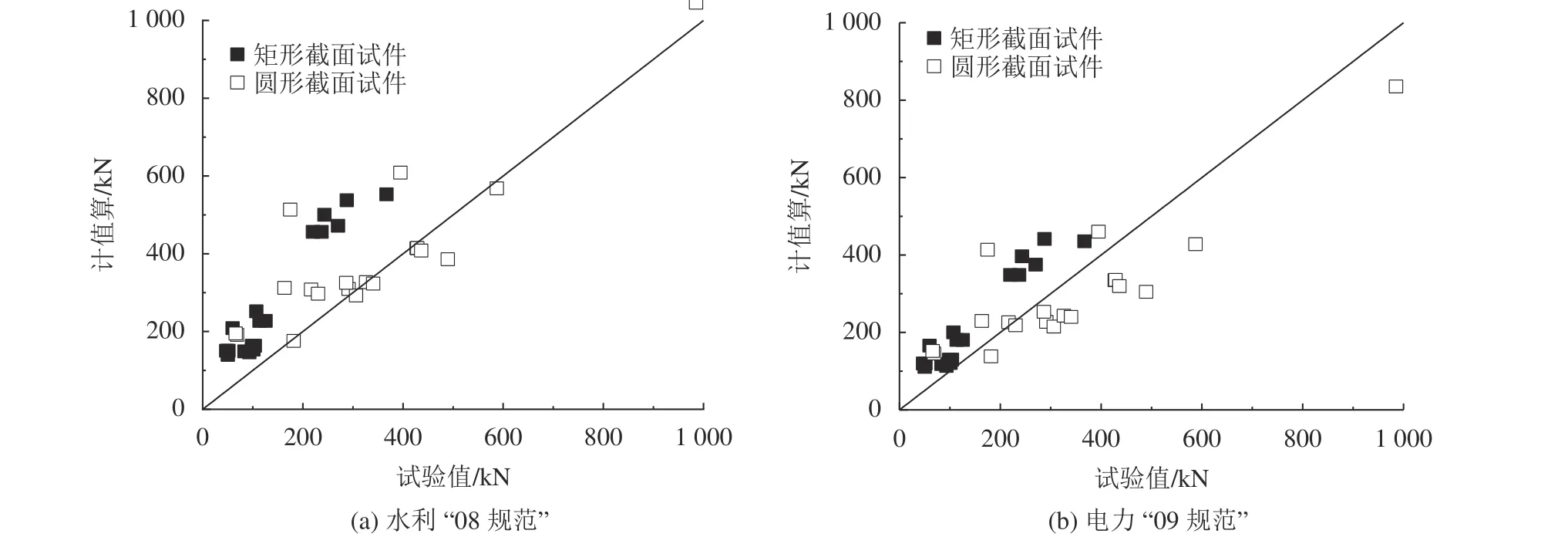
图1 弯剪破坏柱抗剪承载力试验值与各规范公式计算值比较Fig.1 Comparison of shear capacity test values of columns failed in flexural-shear and calculation value of each code formula

如图1所示，对于矩形截面的弯剪破坏RC柱，水利“08规范”[9]和电力“09规范”[10]的抗剪承载力计算值都高于试验值，表明这两个规范的抗剪承载力计算公式都存在较大危险性，对矩形截面RC柱塑性铰区抗剪承载力无保证；对于圆形截面的弯剪破坏RC柱，水利“08规范”[9]和电力“09规范”[10]的抗剪承载力计算值部分低于试验值，说明两规范对圆形截面的RC柱塑性铰区抗剪承载力具有一定的保证率。

为进一步说明水利“08规范”[9]和电力“09规范”[10]抗剪承载力公式的可靠性，对图1中安全范围和危险范围内的RC柱试件个数进行统计分析，计算对于两种截面，抗剪承载力满足要求的试件个数占总试件个数的比例，即保证率。对于矩形截面RC柱，水利“08规范”[9]和电力“09规范”[10]抗剪承载力公式的保证率都为0；对于圆形截面RC柱，水利“08规范”[9]和电力“09规范”[10]抗剪承载力公式的保证率分别为42.11%和63.16%。可以看出：当弯剪破坏RC柱截面为矩形时，采用水利“08规范”[9]和电力“09规范”[10]的抗剪承载力计算公式都非常危险；当弯剪破坏RC柱截面为圆形时，采用水利“08规范”[9]和电力“09规范”[10]的抗剪承载力计算公式也略危险。

另外，统计分析式（2）和（3）抗剪承载力计算值与试验比值的均值和变异系数，见表3。

由表3可知，各规范抗剪承载力计算结果的偏差大小及其离散程度情况如下：

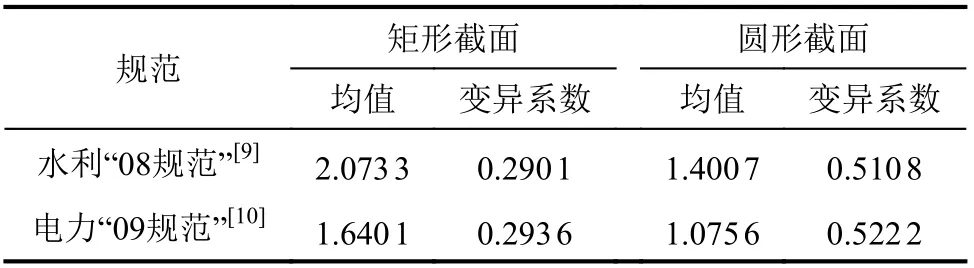
表3 各规范抗剪承载力计算值/试验值的统计分析Tab.3 Statistic analysis of calculated/experimental values of shear capacity of each code

1）不论矩形截面RC柱还是圆形截面RC柱，电力“09规范”[10]抗剪承载力公式偏差的均值比水利“08规范”[9]的小，但电力“09规范”[10]抗剪承载力公式偏差的变异系数比水利“08规范”[9]的大，说明电力“09规范”[10]抗剪承载力计算公式的偏差较小，但偏差的离散程度较大。

2）对于同一规范，圆形截面RC柱的抗剪承载力计算值的偏差较小，而矩形截面RC柱的抗剪承载力计算值的偏差的变异系数较小，这说明，矩形截面RC柱的抗剪承载力计算值的偏差分布离散程度较小。

4 建立RC柱塑性铰区抗剪承载力计算式

由以上分析可知，采用水利“08规范”[9]和电力“09规范”[10]RC柱抗剪承载力计算公式对于弯剪破坏的情况偏危险，因此，引入修正系数k对两个规范的抗剪承载力计算公式进行修正，并采用文献[5]和[22]中的15根弯剪破坏矩形截面RC柱试验数据对修正后的抗剪承载力计算式进行验证。15根弯剪破坏RC柱的基本参数及其抗剪承载力试验值见表4。

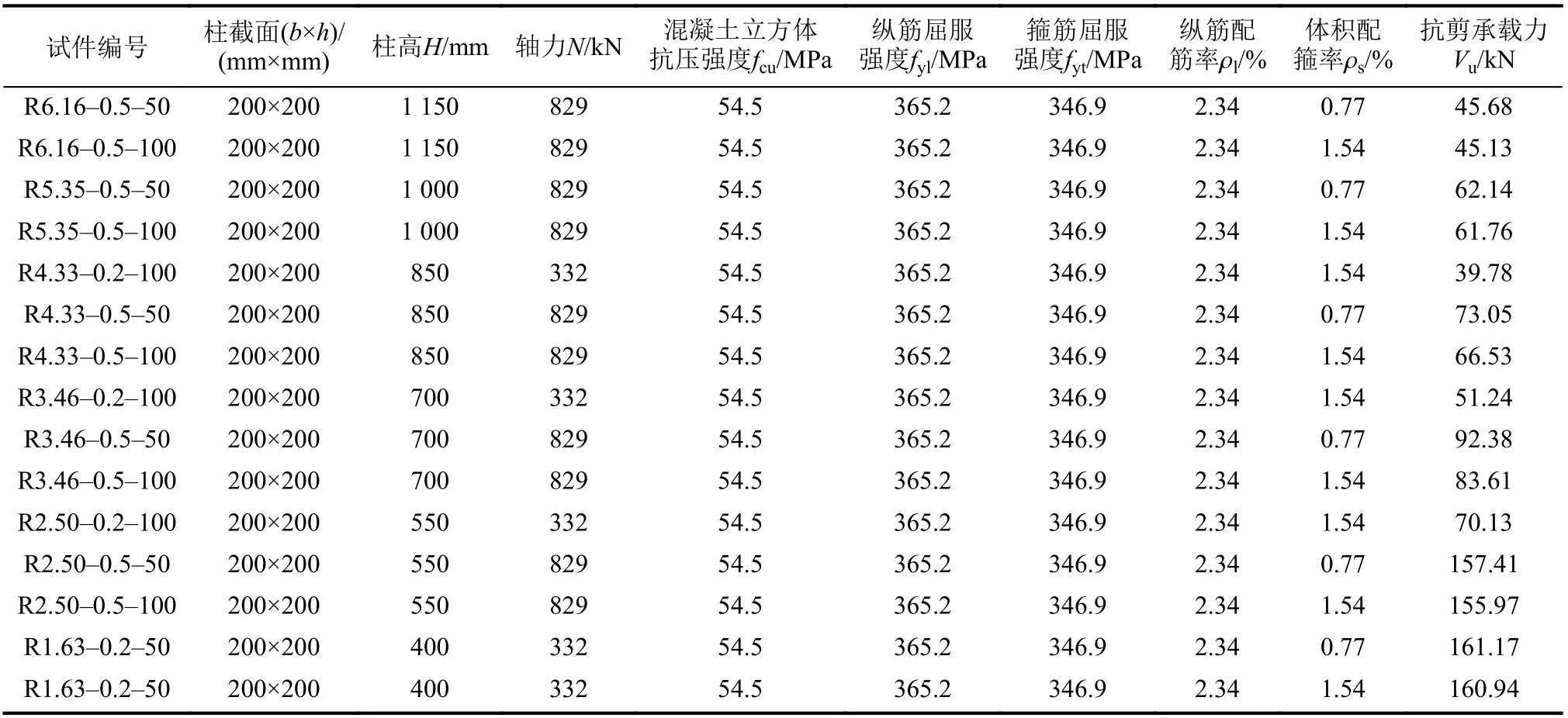
表4 15根弯剪破坏RC柱的基本参数及抗剪承载力试验值Tab.4 Basic parameters and shear capacity test values of 15 RC columns failed in flexural-shear

4.1 建立计算式

柱顶极限位移角是度量RC柱变形能力的主要参数之一，为无量纲参数，可排除柱高因素的影响，并且不同剪跨比的RC柱的极限位移角具有较好的一致性[23]。本文选用柱顶极限位移角表示修正系数，以表示RC柱塑性铰区的抗剪承载力随着延性变形的增加而降低。以柱顶极限位移角δd,Ma为变量建立修正系数k的线性回归方程，极限位移角按文献[24]计算，如式（4）所示：

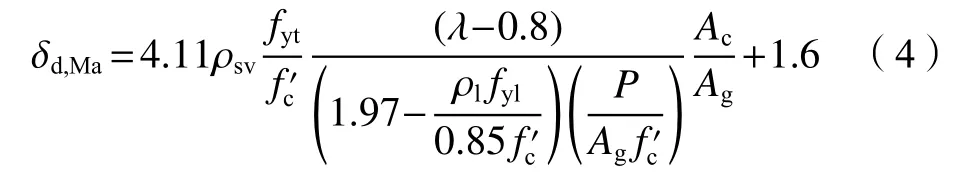
式中，ρsv为配箍率，fyt为箍筋屈服强度，为混凝土圆柱体抗压强度，λ为剪跨比，ρl为纵筋配筋率，fyl为纵筋屈服强度，P为轴向荷载，Ag为柱的全截面面积，Ac为混凝土核心区面积，δd,Ma为柱顶极限位移角。

建立修正系数k关于位移角δd,Ma的线性关系后，需要保证修正后的抗剪承载力计算值不为负值，且抗剪承载力计算值要低于试验值。修正系数k可表示为：

式中，Vcs为混凝土抗剪承载力Vc与箍筋抗剪承载力Vsv之和。

为保证修正后的抗剪承载力计算值低于试验值，选择修正系数k的下限值与极限位移角 δd,Ma进行拟合，如图2所示。

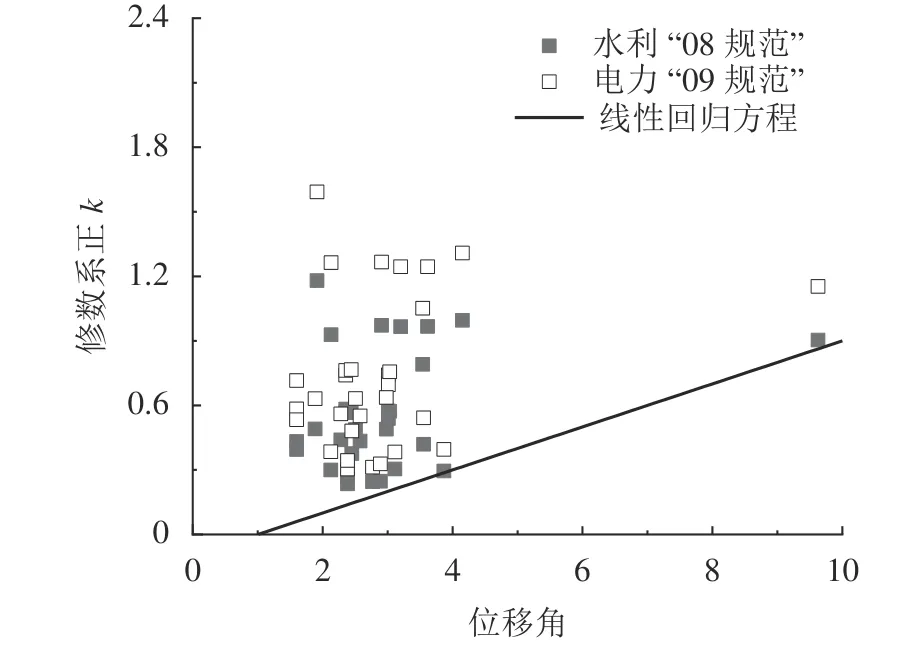
图2 修正系数的线性回归方程Fig.2 Linear regression equation of the modified coefficient

得到线性回归方程为：

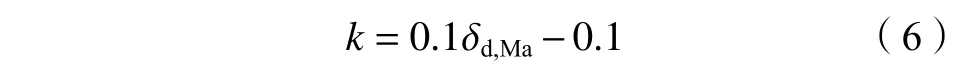
引入修正系数k后的水利“08规范”[9]和电力“09规范”[10]抗剪承载力计算公式如式（7）和（8）所示，参数含义与式（2）和（3）一致。

基于水利“08规范”[9]修正后的RC柱塑性铰区抗剪承载力计算公式为：

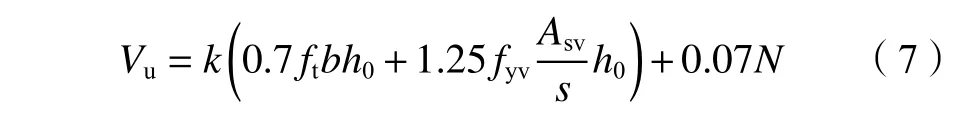
基于电力“09规范”[10]修正后的RC柱塑性铰区抗剪承载力计算公式如下：

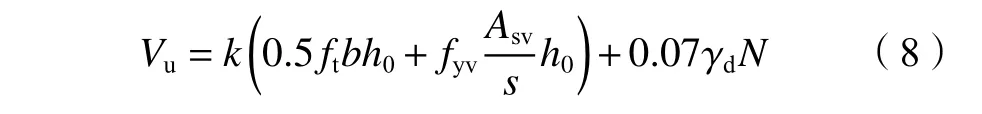
两个水工规范抗剪承载力公式修正前后计算值与试验值的比较如图3所示，可以看出修正后的计算式对弯剪破坏矩形和圆形截面RC柱抗剪承载力的保证率达到100%，满足要求。

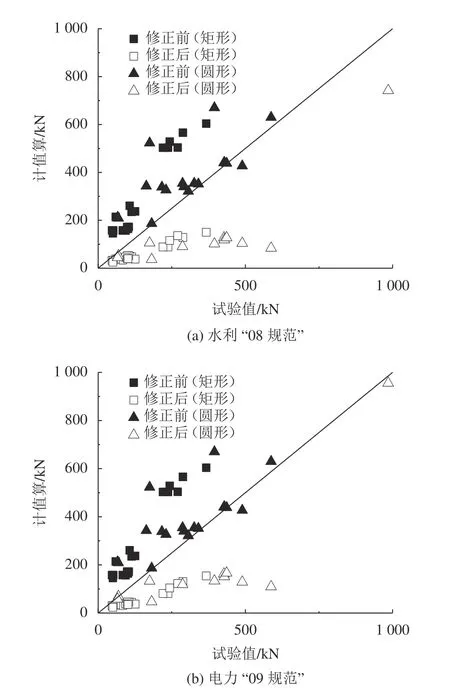
图3 弯剪破坏RC柱抗剪承载力公式修正前后计算结果对比Fig.3 Comparison of calculation results before and after correction of shear capacity formula for RC columns failed in flexural-shear

4.2 验证计算式

为验证修正后计算式对RC柱塑性铰区抗剪承载力的保证率，比较文献[5]和[23]中的15根弯剪破坏矩形截面RC柱修正前后抗剪承载力计算值与试验值，如图4所示。由图4可知，水利“08规范”[9]和电力“09规范”[10]修正前的RC柱抗剪承载力公式的保证率分别为6.67%和20.00%，修正后的比例皆为86.67%，这表明，修正后的计算式对RC柱塑性铰区的抗剪承载力保证率可达到85%。

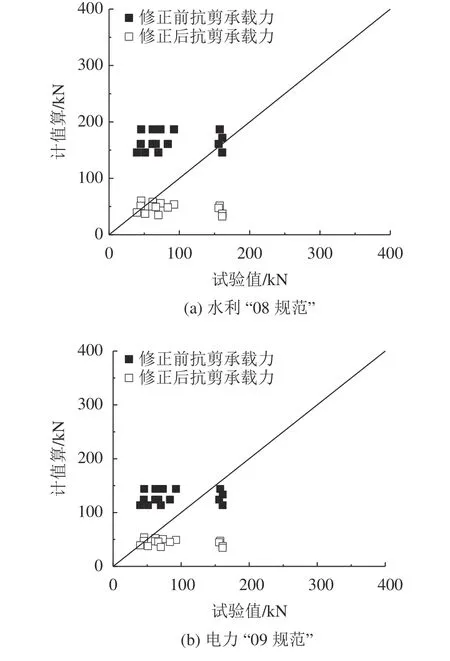
图4 弯剪破坏矩形截面RC柱抗剪承载力修正公式验证Fig.4 Verification of the modified formula for shear capacity of RC columns failed in flexural-shear with rectangular section

本文建立的RC柱塑性铰区抗剪承载力计算式（7）和（8）存在两方面不足：一是，选取的试件数量仍显少；二是，两公式仅适用于预测弯剪破坏RC柱塑性铰区的抗剪承载力，计算前需要判别RC柱的破坏模式。

根据修正式建立时采用的数据范围，对水工RC柱塑性铰区抗剪承载力计算式（7）和（8）适用范围做如下限制：21 MPa≤混凝土圆柱体抗压强度≤86 MPa；240 MPa≤纵筋屈服强度fyl≤510 MPa；240 MPa≤箍筋屈服强度fyt≤690 MPa；0.005≤纵筋配筋率ρl≤0.050；0.002≤体积配箍率ρs≤0.040；1.0≤剪跨比λ≤3.2；0.05≤轴压比n≤0.90。