突破常规思维 培养创新意识*——面积法在中考题中的应用

张 宁

(宁夏中卫市沙坡头区宣和镇东台学校,755000)

《义务教育数学课程标准(2011年版)》指出:创新意识的培养,是现代数学教育的基本任务,应体现在数学教与学的过程之中,学生自己发现和提出问题是创新的基础,独立思考、学会思考是创新的核心[1].笔者认为,课堂是培养学生创新素养的主阵地.在教学过程中,教师引领学生突破常规思维限制,创新问题解决方法,是培养学生创新素养的有效途径.本文以2021年全国各地中考数学试题为例,突破常规解题方法,利用面积法创新求解几何计算问题,为创新素养教育积累课程资源,供读者参考.

一、面积法在中考题中的应用

1.求解与三角形有关的几何问题

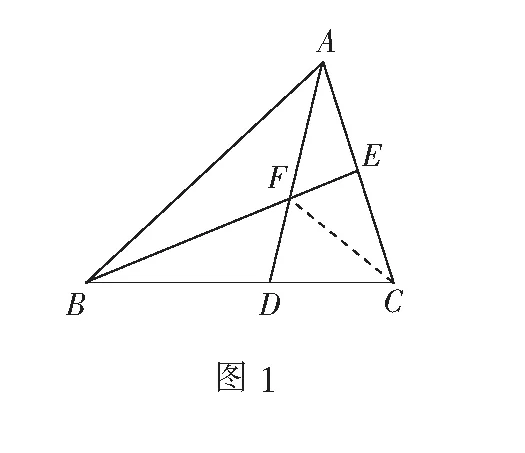
解如图1,连结CF.

令S∆AEF=m,则S∆CEF=m,S∆ABF=3m.

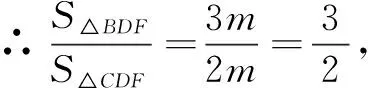
点评本题的常规解法是构造平行线,利用相似三角形的性质或平行线分线段成比例定理求解.这里的解法根据“高相同的两个三角形面积之比等于对应底边之比”解决问题,求解过程通俗易懂,简洁明了.由此可以看出,面积法也是求解线段之比问题的有效方法.这种方法与构造平行线相比,具有一定的创新性,有利于培养学生的创新素养.

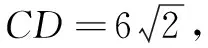
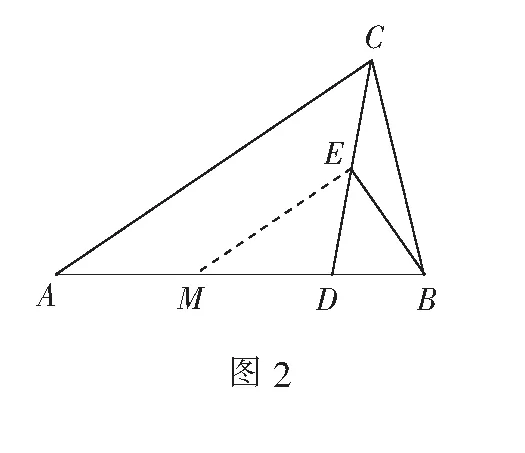
解析如图2,取AD的中点M,连结EM.

由E是CD的中点,可得EM∥AC,

∴∠DEM=∠ACD=∠BED=45°,

即DE平分∠BEM.

令EM=3k,则BE=2k.

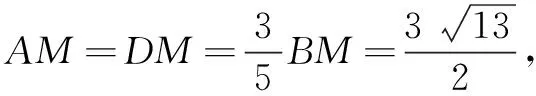
点评本题的常规解法是利用∠ACD=∠BED=45°构造直角三角形,然后利用直角三角形的性质或相似三角形的性质求线段AB的长.这里的解法是根据图形特征,作辅助线EM构造角平分线模型,然后利用角平分线的性质及三角形的面积公式解决问题.

2.求解与四边形有关的几何问题

例3(2021年泸州中考题) 如图3,在边长为4的正方形ABCD中,点E是BC的中点,点F在CD边上,且CF=3DF,AE,BF相交于点G,则∆AGF的面积是______.

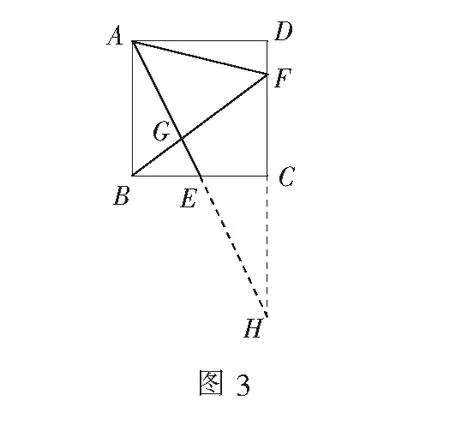
解如图3,延长AE,交DC的延长线于点H.

易知CH=AB=4,CF=3,∴FH=7.

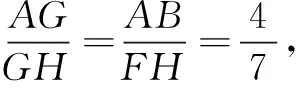
∵S∆AGF+S∆FGH

=S正方形ABCD-S∆ADF=16-2=14,

点评利用面积法求解本题的方法不唯一，具有不同认知水平的学生,可以给出不同的解法.这里的解法将线段之比转化为三角形的面积之比,然后通过列方程求得了三角形的面积,具有一定的创新性.

例4(2021年东营中考题)如图4,正方形纸片ABCD的边长为12,点F是AD上一点,将∆CDF沿CF折叠,点D落在点G处,连结DG并延长交AB于点E.若AE=5,则GE的长为____.

解法1如图4，设DE与CF相交于点H.

由折叠,得DE⊥CF,DH=GH.

易证∆DCF≌∆ADE,

∴DF=AE=5,CF=DE.

在Rt∆DCF中,由勾股定理,得

点评本题的常规解法就是构造直角三角形，利用全等三角形的性质、轴对称的性质、相似三角形的性质等知识求解.上述解法渗透转化思想，是解决这类问题的通性通法，具有普适性.

解法2如图5，连结EF，CE，设DE与CF相交于点H.

由解法1,可知DE⊥CF,DH=GH,DF=AE=5,DE=CF=13.

令GE=x,GH=DH=y,则EH=x+y,DE=x+2y.

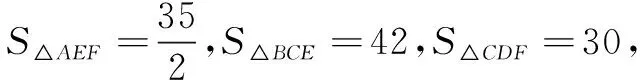
∴S∆CEF=S正方形ABCD-S∆AEF-S∆BCE-S∆CDF

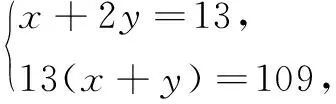
点评由图形的轴对称性,易知DE⊥CF,由此可想到利用面积关系列方程求解.这种解法计算量小,方法新颖独特,求解过程简洁明了,是一种创新解法.

例5(2021年广东中考题)如图6,在ABCD中,过点D作DE⊥AB,垂足为E,则sin∠BCE=______.

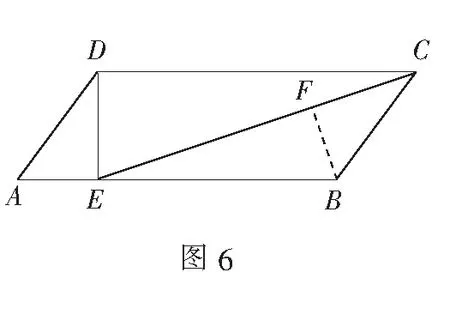
解如图5,过点B作BF⊥EC于点F.

由S平行四边形ABCD=S∆ADE+S∆CDE+S∆BCE，得

由三角函数的定义,易得

点评本题的常规解法是构造直角三角形,将∠BCE或∠BCE的等角转化到某一个直角三角形中,然后利用直角三角形的性质或相似三角形的性质求得这个直角三形的某些边长,最后利用三角函数的定义求得sin∠BCE.而这里利用面积法列方程求解,避免了繁琐的计算,体现了面积法的优越性.

例6(2021年嘉兴中考题)如图7,在ABCD中,对角线AC,BD相交于点O,AB⊥AC,AH⊥BD于点H.若则AH的长为______.

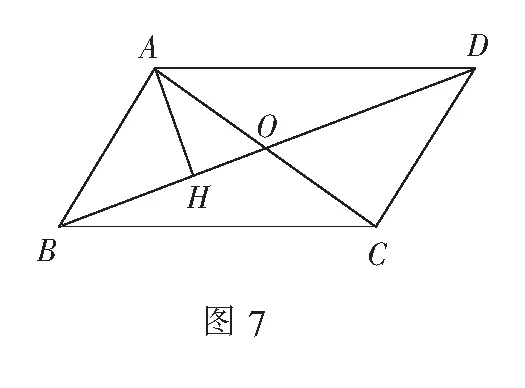
解析由勾股定理,易得

∵四边形ABCD是平行四边形,

在Rt∆AOB中,由勾股定理,可得

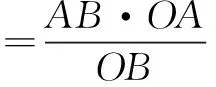
点评线段AH是Rt∆AOB的边OB上的高,故只需求得线段OA和OB的长即可利用面积法求得线段AH的长.这种解法避免了构造辅助线,求解过程简洁明了,是一种非常优

美的解法.

二、结束语

在学习过程中,学生在解决与三角形或四边形有关几何计算问题时,习惯利用直角三角形、全等三角形、相似三角形的有关性质求解.当几何问题中已知量与未知量之间的逻辑关系不明显时,学生习惯构造辅助线,使已知量与未知量之间的逻辑关系外显化,然后再利用直角三角形、全等三角形或相似三角形等基本图形的性质求解.这样容易使学生形成解题套路,遇到几何问题时能快速形成解题思路，但也存在一定的弊端,容易使学生思维僵化,缺乏创新意识和创新能力,不利于培养学生的创新素养.由以上几何问题可以看出,面积法在解决与三角形或四边形有关的几何计算问题时有着广泛的应用.在教学过程中,引导学生用多种方法解决同一类问题,对培养学生的创新素养大有裨益.面积法其实质是将某一几何图形的面积“算两次”[2],由结果相等可构造等量关系,为解决问题提供便利条件.当几何图形中某个三角形的面积易用有关线段表达时,可考虑将这个三角形的面积“算两次”,然后通过列方程解决问题,这种方法具有化难为易、化繁为简的作用,能够达到事半功倍的效果.