也谈反比例函数背景下三角形面积问题新解

高爱香

(山东省邹城市第九中学,273500)

笔者拜读了贵刊上的文献[1]及[2],受益匪浅.本文受文[2]的启示,在文[1]的基础上通过深入探究、推演,得到反比例函数图象上任意两点与坐标原点(三点共线除外)连结而成的三角形面积的计算公式,并利用此公式快捷地解决相关中考试题.

一、三角形面积公式及其推导

文[1]给出了函数背景下斜三角形的面积公式:

①

②

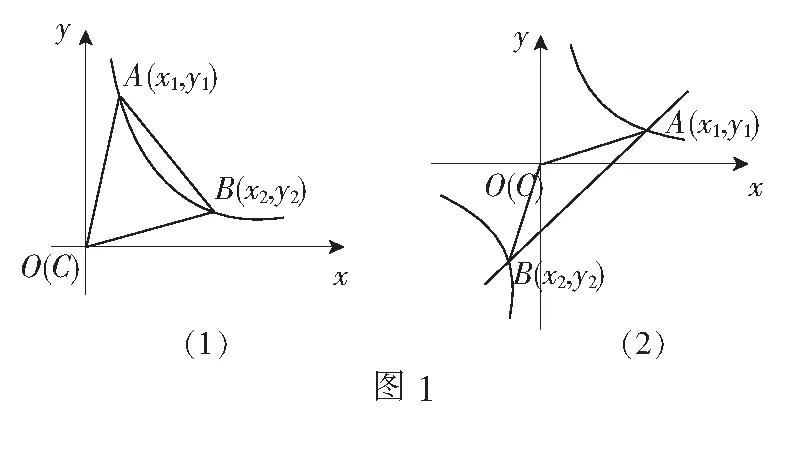
证明由A，B为直线y=ax+b(a≠0)上的两点,可知

b=y1-ax1

由公式①,得

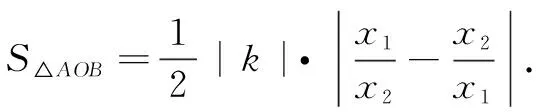
二、公式应用

上述公式简洁对称,形式优雅,易于记忆.我们只要知道反比例函数的解析式及其图象的任意两点的横坐标(或这两点横坐标的倍分关系),就可求出双曲线上任意两点与原点(三点共线时除外)连结而成的三角形的面积.下面通过中考实例说明其应用.

例1(2021年南充中考题)如图2,反比例函数的图象与过点A(0,-1),B(4,1)的直线交于B,C两点.

(1)求直线AB和反比例函数的解析式;

(2)已知点D(-1,0),直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求∆BCE的面积.

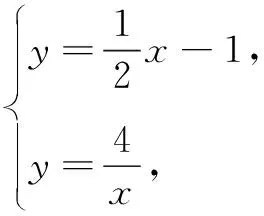
由D(-1,0),C(-2,-2),可得yCD=2x+2.

∴E(1,4).

如图2,连结OB,OC,OE.

由公式②,得

S∆BCE=S∆BOC+S∆COE+S∆BOE

解析如图3,过点C向x轴作垂线,交x轴于点E,连结OD,则CE∥AB.

∵C是OA的中点,

∴S∆COD=S∆ACD=2,

即点D的横坐标是点C横坐标的2倍.

由公式②,得

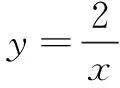
由公式②,得

又∆ABP的面积是∆AOB的面积的2倍,

∴t2+t-2=±2t.

当t2+t-2=2t时,解得t=2;

当t2+t-2=-2t时,

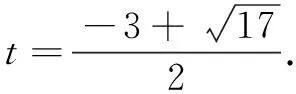
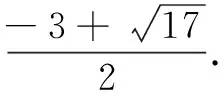
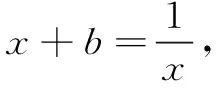
∴x2+bx-1=0.

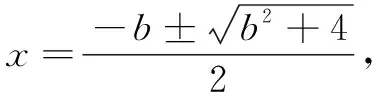
∴A,B两点的横坐标分别为

由公式②,得

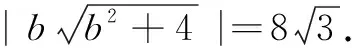
两边平方,得b4+4b2-12×16=0,

∴(b2-12)(b2+16)=0,

评注例3、例4中的常规解法,需要进行分类讨论.例3分点P在点B的上方或下方两种情况进行解答;例4按直线y=x+b交于y轴的正半轴或负半轴进行分类讨论.部分学生由于受思维定势的影响出现了漏解的情况,而运用本文中两则公式解答则可避免因分类讨论而产生漏解的情况,提高了解题的准确性.

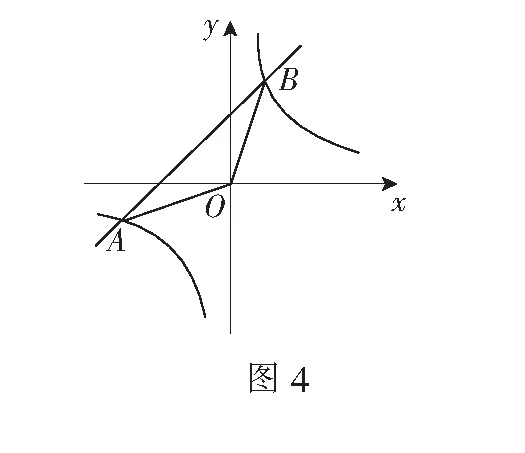
解析由反比例函数的中心对称性,可知OA=OB.

如图5,连结OE,则由直角三角形斜边的中线的性质,可以推出∆AOE为等腰三角形,∴∠OEA=∠OAE=∠EAC, ∴OE∥AC.

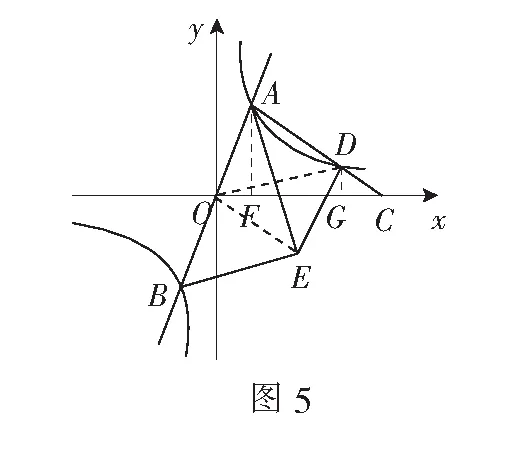
连结OD,则S∆OAD=S∆EAD=8.

分别过A,D两点向x轴作垂线,交x轴于点F,G,则有AF∥DG,

∴AF∶DG=CA∶CD=3∶1,

∴AF=3DG.

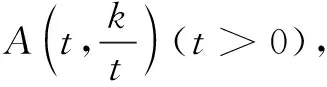
整理,得k=6(负值舍去).

三、结束语

在解决数学问题的过程中,我们除了能熟练、合理、灵活地运用课本上直接或间接给出的结论外,还应该重视从课本例题以及有关数学试题中提炼出来的结论.这些结论,对帮助我们快速找到解题的思路或突破口,特别对选择、填空题,往往能起到事半功倍的效果,同时也是培养学生应用意识的一个有效途径.因此,教师在教学过程中,不仅要注意引导学生学会应用数学结论解决数学问题,同时也要注意引导学生去发现数学结论,并及时提炼总结数学结论,进而应用发现的数学结论指导我们解决问题.这不仅有助于激发学生的学习兴趣,提高解题效率,而且对发展学生的数学思维能力,培养数学创新意识、应用意识具有重要的现实意义.