基于Copula 函数风险组合的西峡县山洪灾害预警分析
2022-11-28张玉昶荣富强王明闪王建国
张玉昶,荣富强,王明闪,王建国,万 芳
(1.河南省地质矿产勘查开发局第二地质环境调查院,河南郑州 450000;2.华北水利水电大学水资源学院,河南郑州 450011)
近年来,极端气候频发,导致山洪灾害越来越频繁发生,山洪灾害已经成为世界各国自然灾害中的主要灾种之一,造成了大量的人员伤亡和社会经济损失[1],为了防御山洪灾害,减轻灾害损失,国内外许多专家学者对山洪灾害预警进行了研究。王协康等[2]采用TRI-GRS 模型分析了小流域的滑坡易发性,将暴雨山洪洪水划分为预警区、中、高风险区。我国下垫面等条件复杂多样,山洪灾害成灾机理复杂,而临界雨量是山洪灾害的主要影响因素。目前,临界雨量的计算方法主要有数据驱动法及水文水力学法[3,4]。但是,临界雨量受前期影响雨量影响较大[5],江锦红等[6]采用双曲函数确定的暴雨临界雨量最为山洪灾害的预警标准;刘媛媛等[7]针对小流域,利用临界流量及水位计算相应的临界频率;张珊珊等[8]基于HEC-HMS 模型,研究选用雨量预警指标,综合考虑土壤含水量、汇流时间等,反推临界雨量。临界雨量的研究成果丰硕,但是未考虑到几种风险组合情况的临界雨量及相应的预警分析。水文科学领域的种随机变量之间往往呈现出各种复杂的线性、非线性的相关关系,本文引入Copula 函数来描述降雨量与峰值雨强变量间的相关性,Copula 函数可将联合分布的函数和它各自的边缘分布函数联系在一起,基于变量之间的非线性相关关系而建立的,可以描述变量间非线性、非对称和对称的相关关系,目前在水文科学中得到广泛的应用[9-11]。
1 研究区概况
西峡县位于河南省西南边陲,与陕西省接界,地处秦岭山系东南余脉伏牛山南。东南与本市的内乡、淅川相连,北西与栾川、卢氏和陕西省的商南县毗邻。地处北亚热带向暖温带的过度地区,属于亚热带季风型大陆性气候,季风影响明显,四季分明,春季温度升降剧烈,雨水分布不均,夏季热雨集中,暴雨频发,地质地貌复杂,加上受人类活动的影响,导致山洪灾害发生频繁。山洪灾害在县境内分布广,具有来势猛、流速快、破坏力大、突发性强的特点,预报、预测、预防难度较大,不仅对山区的基础设施造成毁灭性破坏,而且对人民群众的生命安全构成极大的威胁,已经成为当前防灾减灾工作中的突出问题,是山区经济社会可持续发展的重要制约因素之一。
西峡县山洪灾害致灾因素具有自然地理和经济社会的双重属性,降雨因素是诱发山洪灾害的直接因素和激发条件。降雨量大,多数情况下意味着雨强高、激发力强,在一定的下垫面条件下,易产生溪河洪水灾害、泥石流灾害和滑坡灾害。根据西峡县近年来的统计资料表明,每次山洪灾害的发生,都是在降雨量较大这一基本前提条件下形成的;高强度的降雨是引起山洪灾害的最主要原因之一。
在相同的条件下,降雨历时越长,降雨量越大,产生的径流量越大,山洪灾害损失也越严重。在溪河洪水、泥石流、滑坡三种山洪灾害类型中,溪河洪水灾害和泥石流灾害特点相似,在下垫面条件满足的情况下,只要有足够大的降雨强度和降雨量,溪河洪水和泥石流灾害就可发生,降雨历时越长,所产生的洪量越大,灾害损失越大。滑坡灾害与降雨历时的关系更为明显,一般而言,滑坡和降雨并不是同时发生,滑坡一般滞后于降雨,由溪河洪水诱发的滑坡灾害会随着降雨历时的增长,洪流对坡脚的掏蚀,滑坡也会越来越多。
2 混合Copula 函数的风险组合概率的临界雨量确定
2.1 Copula理论及Copula函数分布模型
1959年Copula函数理论提出,Sklar提出可把一个联合分布函数分解为一个Copula 函数和K个边缘分布函数,而分解出来的Copula 函数可用来描述变量之间相关性,也就是可将联合分布的函数和它各自的边缘分布函数联系在一起的函数。N元Copula函数C(u1,u2,…,uN)具有以下性质:

常用的Copula 数有很多种,本文主要介绍常用的多元正态Copula 函数、阿基米德Copula 函数Archimedean 的三类常用函数(Clayton 函数、Gumbel Copula 函数、Frank Copula 函数)和极值Copula函数。
(1)多元正态Copula函数。其中N元正态Copula函数的分布函数与密度函数可表达为:
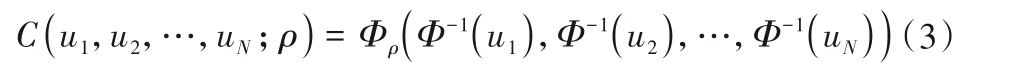
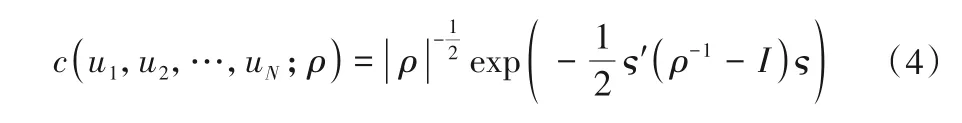
式中:ρ为对角线上的元素为1的对称正定矩阵;|ρ|表示与矩阵ρ相对应的行列式的值;Φρ(⋅)表示相关系数矩阵为ρ的标准正态分布函数;Φ-1(⋅)为标准多元正态函数Φ(⋅)的逆函数;ς=(ς1,ς2,…,ςN)′,ςn=Φ-1(un),n=1,2,…,N,I为单位矩阵。
(2)阿基米德Copula函数。其中阿基米德Copula函数可表示为:

Gumbel Copula 函数、Clayton Copula 函数、Frank Copula 函数是常用的二元阿基米德Copula 函数,分别由它们扩展到N元阿基米德Copula函数可表示为:
①N元Gumbel Copula函数的表达式为:
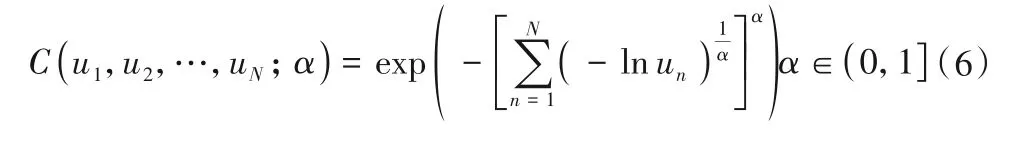
②N元Clayton Copula函数的表达式为:
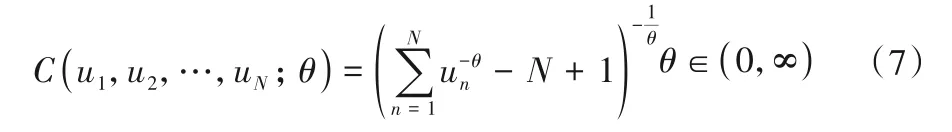
③N元Frank Copula函数的表达式为:
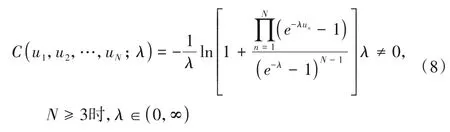
其中,α,θ,λ为相关参数。
(3)极值Copula 函数。极值Copula 函数(Extreme Value Copula,EVC)可表达为:
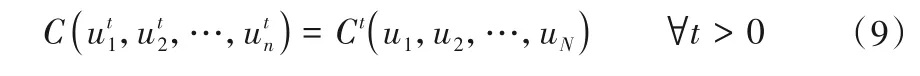
2.2 混合Copula函数的构造与相关性分析
(1)不同类型的Copula 函数比较分析。一般情况下,多元正态Copula 函数通常描述变量之间的相关关系,但是由于此函数有对称性的特点,所以对于变量的非对称相关关系很难拟合。
而Gumbel Copula 函数和Clayton Copula 函数都具有非对称性的特点,其中Gumbel Copula函数为“J”字形分布,下尾低而上尾高,对水文变量的下尾部变化不太敏感,而对上尾部的分布变化比较敏感,所以很难描述下尾部的相关变化情况,即当一个水文变量出现极大值时,另外两个水文变量也出现极大值的概率增大;
Clayton Copula 函数为“L”字形分布,下尾高而上尾低,对水文变量的下尾部变化比较敏感,而对上尾部的分布变化不太敏感,所以很难描述上尾部的相关变化情况,即当一个水文变量出现极小值时,其他4个水文变量也出现极小值的概率增大。
Frank Copula 函数为“U”字形分布,它有对称性的特点,所以很难描述水文变量之间的非对称关系,Frank Copula 函数只适合描述具有对称相关结构的变量之间的相关关系,即各个水文变量间极大值相关性与极小值相关性是对称增长的,但是其尾部的分布变量是比较独立的,所以Frank Copula 函数无论在描述上尾部还是下尾部的相关性中都是不敏感的,故无法描述尾部变化的相关性。
(2)混合Copula 函数的构造与相关性分析。Gumbel Copu‐la 函数、Clayton Copula 函数、Frank Copula 函数三类常用的阿基米德函数能够捕捉尾部相关的情形:上尾部的相关、下尾部的相关、上尾部和下尾部的对称相关。这些Copula 函数具有描述各种水文变量模式之间的关系,特别是尾部相关关系,水文系统中各变量之间的关系是复杂多变的,不是拘泥于某种特定关系,它们只能反映水文变量间相关性的某个侧面,因此很难用一个简单的Copula 函数来全面的刻画水文系统中各变量之间的相关模式,所以一个更加灵活的Copula 函数需要构造,来描述各种水文变量模式之间的关系。应用不同Copula 函数的优点,本文选用Gumbel Copula 函数、Clayton Copula 函数、Frank Copula 函数的线性组合来构造混合的Copula 函数,可以更加灵活的刻画水文系统中各变量之间的相关关系。
混合Copula函数M-Copula表达式为:
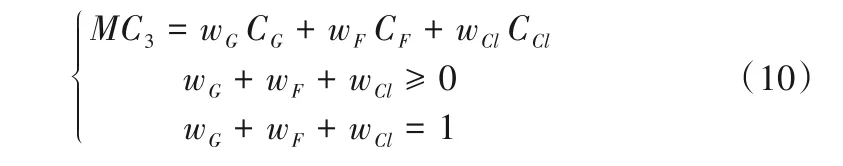
式中:CG,CF,Ccl分别为Gumbel Copula、Frank Copula、Clayton Copula 函数;wG,wF,wcl为相应Copula 函数的权重系数。由式(8)~(10)可知,MC3中包括了6 个参数,参数向量(α,λ,θ)用来描述变量间相关的程度,变量间相关的模式由线性权重参数向量(wG,wF,wcl)表示。
2.3 Copula模型的参数估计、检验与评价
(1)Copula 模型的参数估计。Copula 函数模型中的参数估计有很多种,一般采用极大似然和矩估计,而其中极大似然估计是较常用的Copula 模型参数估计方法,其联合分布函数的密度函数为:
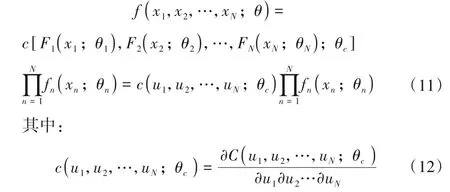
式中:θc为Copula 函数的1 ×mc维参数向量;Fn(xn;θn)为边缘分布函数;θn为边缘分布函数Fn(xn;θn)的1 ×mn维参数向量;θ=(θ1,θ2,…,θN,θc)′;n=1,2,…,N。
因此,可以得到样本(x1t,x2t,…,xNt),t=1,2,…,T的对数似然函数为:
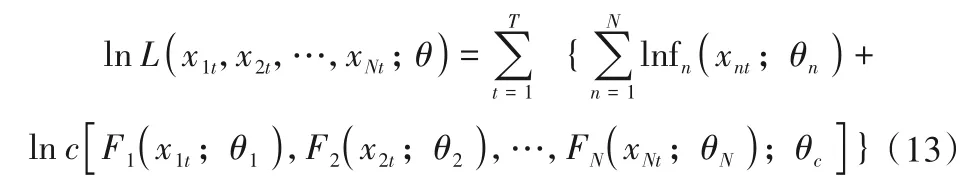
使似然函数取的最大值的θ即是最大似然估计值。
(2)Copula 模型的检验与评价。应用的Copula 分布函数是否能够很好的拟合变量之间的相关结构及分布,所以Copula 函数的检验与拟合优度评价需要建立。K-S用于检验样本是否服从同一分布,故应用其对Copula 分布函数进行检验;Copula 函数的拟合度评价采用均方根误差RSME最小准则来计算,其定义如式(14):
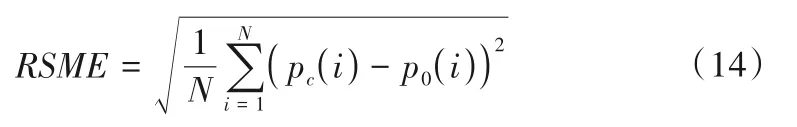
式中:N是样本容量;i为样本序号;pc为模型计算的理论频率;p0为联合分布的经验频率。
其中K-S检验的统计量D计算公式如(15)式所示:
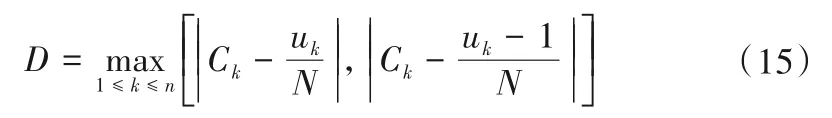
式中:N为样本容量;Ck为样本xk=(x1k,x2k,x3k)的Copula 值;uk为样本中满足条件x≤xk的个数,即满足:x1≤x1k,x2≤x2k,x3≤x3k。
2.4 风险组合概率的临界雨量确定
设随机变量X,Y分别服从边缘分布FX(x)、FY(y),其联合分布函数为F(x,y),其中X表示总雨量,Y表示峰值雨强,则存在一个Copula函数:
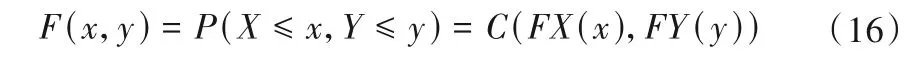
临界雨量中总雨量和峰值雨强存在多种耦合情况,可以运用上述的联合概率分布模型计算出它们的联合分布概率,本文主要考虑超过概率和条件概率,即当总雨量X超过某特定值的条件下,峰值雨强超过某特定值时该雨型发生的条件概率,如式(17)所示。
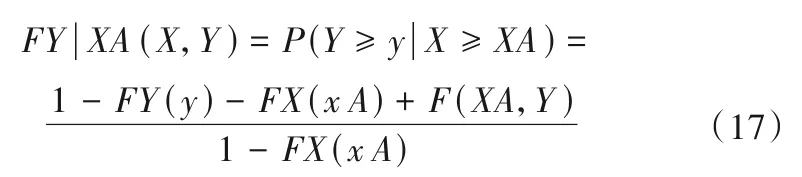
式中:XA表示概率为AA的总雨量值;y表示某特定峰值雨强值。
由此,雨型风险组合概率(A,B)的定义为:
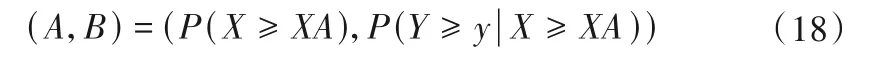
在山洪灾害预警预报中,通常利用重现期对暴雨量级进行描述,对于超过概率,重现期计算公式如下式所示。
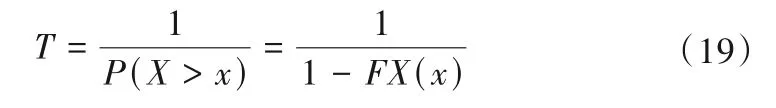
3 西峡县基于临界雨量的山洪灾害预警分析
3.1 Copula函数的选择
分别采用Gumbel、Clayton、Frank 及混合Copula(M-Copula)函数构建12 h 场次降雨量和峰值雨强联合概率分布模型,K-S检验统计量及拟合优度评价指标计算结果如表1所示。
表1 计 算 表 明,Gumbel-Copula、Clayton-Copula、Frank-Copula、M-Copula 函数均通过K-S 检验,能较好的拟合临界雨强的边缘分布,根据均方根误差RSME最小准则,选取M-Copu‐la函数为连接函数来拟合降雨量与峰值雨强联合分布情况。
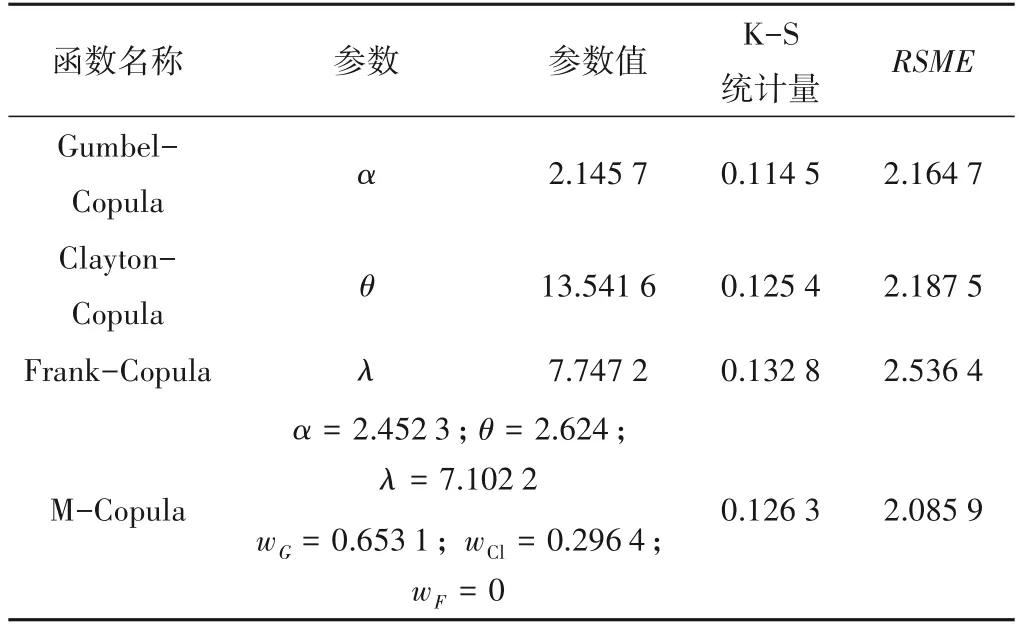
表1 Copula概率分布函数的计算、检验与评价结果Tab.1 Calculation results,inspection and evaluation of Copula cumulative distribution function
3.2 组合概率的临界雨量的风险预警计算
综合考虑防灾对象所处河段河谷形态、洪水上涨速率、预警响应时间和站点位置等因素,在临界雨量的基础上综合确定准备转移和立即转移的预警指标;并利用该预警指标进行暴雨洪水复核校正,以避免与成灾水位及相应的暴雨洪水频率差异过大。
通常情况下,由于临界雨量是从成灾水位对应流量的洪水推算得到,故在数值上认为临界雨量即立即转移指标;对于准备转移指标,是在临界雨量基础上根据准备转移时间及洪水过程线综合进行“折减”处理。
以军马河乡白果村回龙湾组为例,在不同的土壤含水量的情况下,利用风险概率雨型分别计算1、3、6、24 h 临界雨量,其临界雨量预警阈值见表2 所示;水位预警阈值见图1 所示;准备转移预警和立即转移预警雨量临界线图见图2所示。
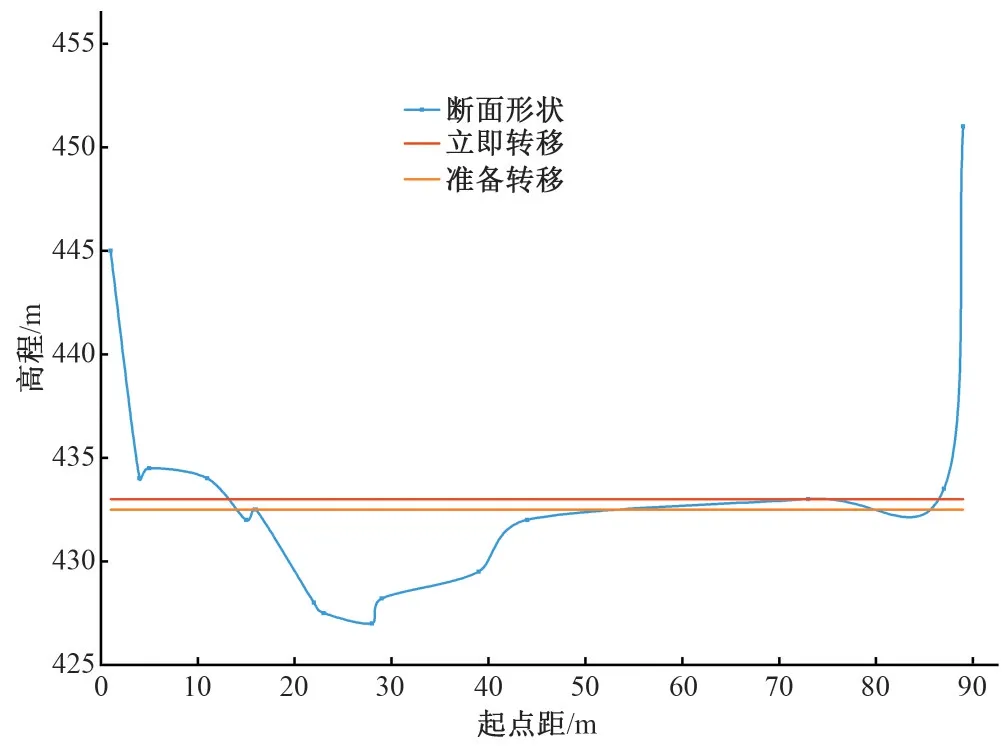
图1 水位预警阈值图Fig.1 Threshold map of water level warning
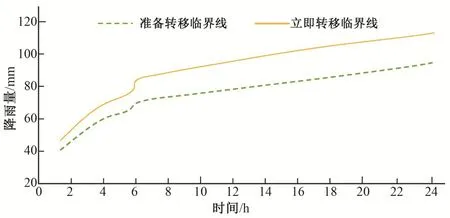
图2 准备转移预警和立即转移预警雨量临界线图Fig.2 Threshold maps for the preparation and immediate diversion of early warning rainfall
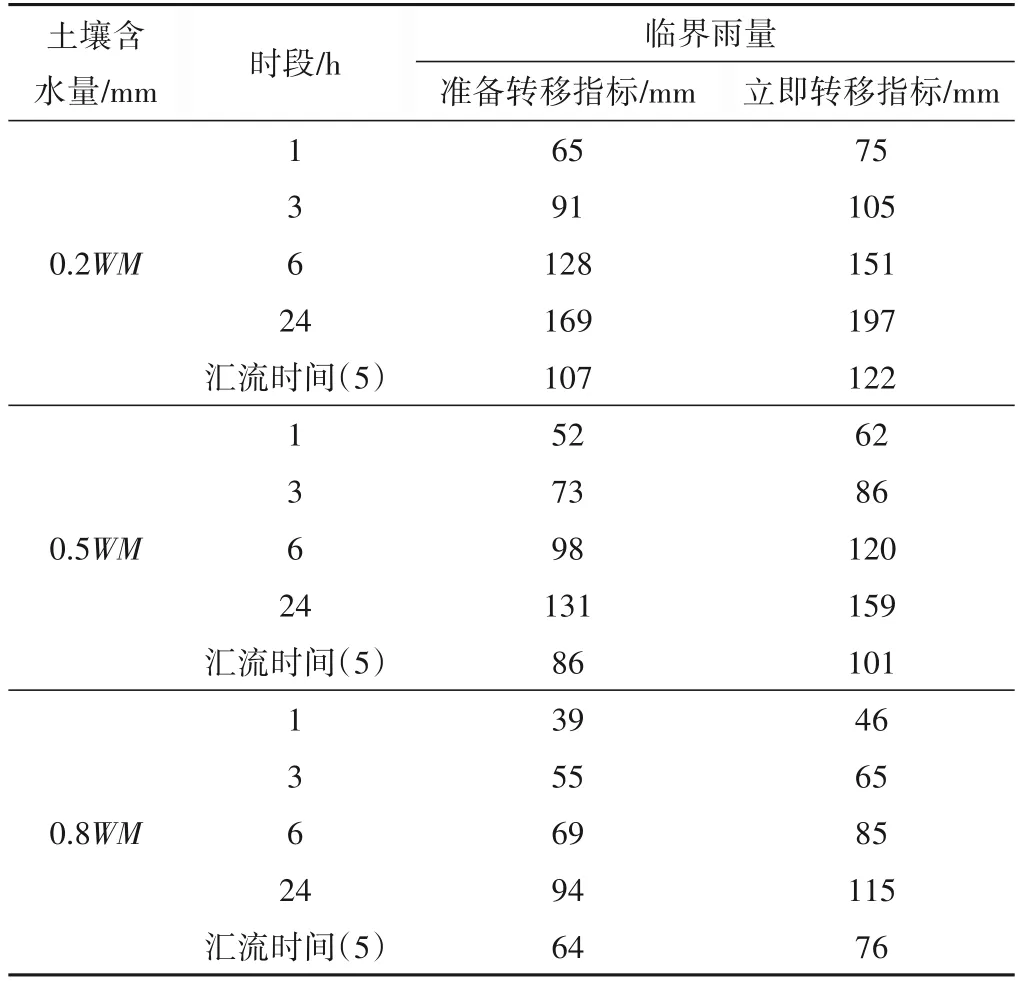
表2 临界雨量预警阈值表Tab.2 Table of critical rainfall warning thresholds
3.3 结果合理性分析
对于山丘区河流洪峰模数具有一定的规律,流域面积越大,洪峰模数越小,面积越小,洪峰模数越大。由此可以根据河南省山丘区水文断面的洪峰模数统计资料,间接评估设计洪峰流量的合理性。根据以往经验资料,50年一遇的中小河流断面的设计洪峰流量对应的洪峰模数一般在10.0 左右,并且10.0 以下占多数。回龙湾组计算得到洪峰模数为8.86,因此设计流量计算成果是合理的。

表3 回龙湾组计算成果合理性分析Tab.3 Analysis on rationality of calculation results of Huilongwan
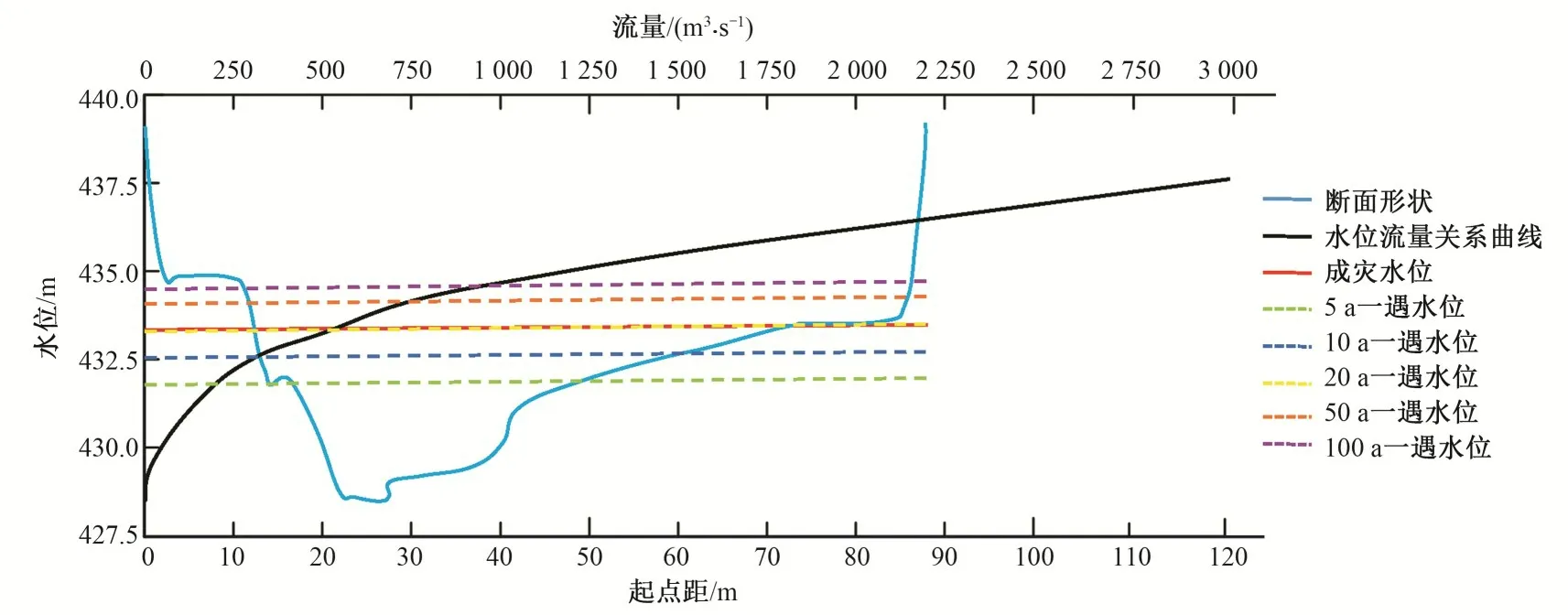
图3 各级水位对比图Fig.3 Comparison chart of water level at different stages
4 结论
通过对西峡县的山洪灾害预警分析可知:混合Copula 函数可以更加灵活的刻画水文系统中各变量之间的相关关系,Copula 分布函数能够很好的拟合总雨量和峰值雨强的二维联合分布函数变量之间的相关结构及分布,根据均方根误差RSME最小准则,选取M-Copula 函数为连接函数来拟合临界雨量联合分布情况;基于对西峡县军马河乡白果村回龙湾组为例进行的计算及分析,计算组合概率的临界雨量,并对山洪灾害的水位、准备转移预警及立即转移预警雨量临界进行预警及分析。结果表明:对于山丘区河流洪峰模数具有一定的规律,流域面积越大,洪峰模数越小,面积越小,洪峰模数越大,设计流量为639 m3∕s 的计算成果是合理的。因此,对山洪灾害预警分析要最大限度的保证人民群众的安全,分析评价中以各沿河村落涨洪历时为基础,分析沿河村落暴雨洪水预警响应时间及其分布情况,这对山洪灾害防治预案编制及预警等均具有重要作用。
