空心包体式钻孔应力解除法数值模拟研究

2022-11-28孙中想张朝贤侯明勋

人民黄河 2022年11期

孙中想，张朝贤，侯明勋

（上海交通大学船舶海洋与建筑工程学院，上海 200240）

地应力是天然岩体在工程建设开挖或扰动之前所具有的自然应力状态，也是岩体与其他人工材料的本质区别之一，虽然地应力在本质上是一种内应力，但从历史进程来看又是一种残余应力［1］。由于地应力是地质环境和工程稳定性评价的重要基础指标，因此黄河中上游地区大型水利枢纽工程建设过程中都十分重视地应力测量研究工作［2－4］。弄清工程区域的地应力分布特征在水利水电工程设计、围岩稳定性分析、岩体结构设计优化等方面具有重要意义［2－5］。地应力的成因和分布极其复杂［6－7］，尽管在总体上有一些规律可循，但获得工程区域相对准确地应力的方法主要还是现场实测。

目前，比较常用的地应力测量方法当属水力压裂法［6－10］和应力解除法［1，6－7，9－11］。应力解除法是根据弹性岩石力学理论建立的应力测量方法，可以在一个单孔、两个或三个非平行钻孔中确定测点的全应力状态，其中发展时间最长、技术上比较成熟的是套芯应力解除法。根据测量原理和被测物理量及其部位的不同，套芯应力解除法又可分为钻孔孔壁应变测量法、钻孔孔径变形测量法和钻孔孔底应变测量法［6－7］。孔壁应变测量法可以在单一钻孔中获得测点的全应力状态，因而在岩石工程中得到了普遍应用，但鉴于存在现场应变片粘贴等问题，不可避免地给测点地应力的计算带来误差。本文以工程中常用的空心包体式钻孔应变计为例，采用有限元数值模拟方法对钻孔应力解除法进行了系统研究，详细分析了实测孔壁变形经过不同介质的传递后对地应力测量计算造成的影响，讨论了对地应力测量结果进行修正的必要性，以期为空心包体式钻孔应变计结构优化设计及其工程应用提供参考。

1 空心包体式三向应力计地应力测量原理

1.1 套芯应力解除法简介

套芯应力解除法地应力测量基本过程如图1所示。在巷道或隧洞里往围岩中钻一个直径较大（110～130 mm）的钻孔；当远离应力扰动区域后，在大孔孔底钻一个直径为36～38 mm的同心测量小孔，此小孔内安装用于感知岩体变形的测量探头；探头安装完毕并且在满足测试的条件下，沿大孔孔壁进行套钻并实施应力解除作业；在套钻过程中安装在小孔内的测量探头能够获得并记录围岩变形数据，据此可以确定测点的地应力张量。安装在小孔内的测量探头有多种类型，其中用于三维地应力测量的有代表性的测量探头是南非黎曼研制的三轴孔壁应变计［12］和澳大利亚CSIRO空心包体应变计［7，10，12］。前者将应变片直接粘贴在钻孔岩壁上，对岩体完整性要求较高，测量精度受到应变片粘贴效果的影响［7］；后者将应变片嵌固在应变计胶筒内，现场利用环氧树脂胶水与岩壁黏结，能够应用在较为破碎的岩体中，因而得到了广泛的应用［13－16］。

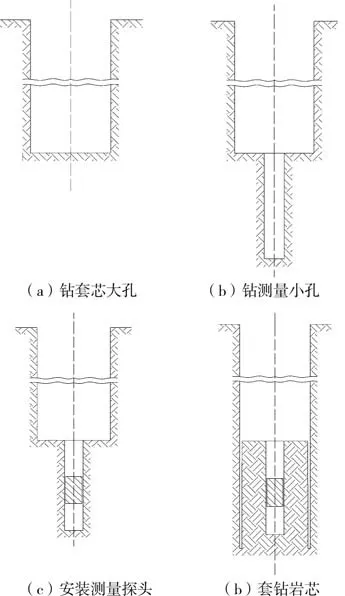
图1 套芯应力解除法地应力测量基本过程

1.2 空心包体式钻孔应变计结构

常用的空心包体式钻孔应变计结构如图2所示，其主体是一个长度为240 mm的预制空心圆筒，外径为34 mm、内径为30 mm、壁厚为2 mm。应变片布置方式如图3所示，一般将3组应变花（图3中①～③）相隔120°角嵌入应变计胶筒中，每组应变花包含4个应变片（图3中1～12），角度可以设置为0°、45°、90°、120°，当然也可以根据需要采用其他分布形式［7］。在具体应用时，应变数据多利用放置在试验孔外的应变仪进行采集；也可以将电子罗盘和变形采集模块微型化集成安装在探头的端部实现数据采集本地化，以避免长距离传输带来的信号损失，从而提高测量精度。

图2 空心包体式钻孔应变计结构示意

图3 空心包体探头应变片布置

1.3 地应力张量的测定

空心包体式钻孔应变计是根据感测套芯应力解除过程中孔壁的变形响应来获得测点的三维地应力张量的。计算时可根据钻孔围岩的二次应力场［7］及胡克定律等［6－7］，确定空心包体式钻孔应变计地应力测量的观测值方程［7，15－16］：

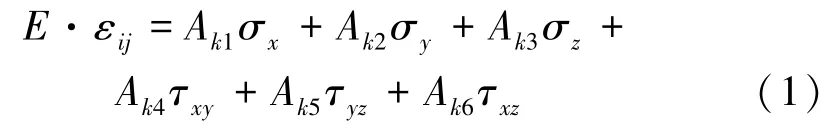
式中：E为岩体弹性模量；εij为应变观测值；k＝4（i－1）＋j，i为应变花编号（i＝1，2，3），j为同组应变花中应变片编号（j＝1，2，3，4）；σx、σy、σz、τxy、τyz、τxz为钻孔坐标系下地应力分量；Ak1～Ak6为应力系数。

应力系数可以表示为

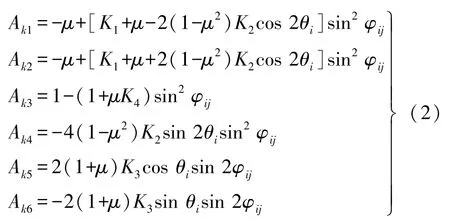
式中：μ为岩体泊松比；θi和φij分别为应变片的极角及应变片与钻孔轴向的夹角；Kn（n＝1，2，3，4）为应力计算修正系数。

由上文可知，由于空心包体式钻孔应变计的应变片嵌入环氧树脂涂层内，孔壁的变形经过现场黏结剂层和环氧树脂涂层传递，因此若想精确获得孔壁的实际变形，须进行必要的修正以减小误差。空心包体式钻孔应变计的应力计算修正系数首先由Worotnick等［17］提出，并被引入三维地应力计算模型中。Fama等［18］给出了修正系数的精确数学解算方法。

空心包体式钻孔应变计一次测量可以建立12个方程，其中独立方程至少有6个，可以利用最小二乘法解算出6个地应力分量，据此确定测点的三维地应力状态，进而得到主应力的量值与方向。

2 钻孔应力解除法有限元数值模拟

2.1 有限元模型的建立

根据空心包体式钻孔应变计地应力测量原理建立有限元数值分析模型。应力解除的整个过程比较复杂，应力解除作业相当于在无限大岩体中对局部的一小段岩芯进行卸载的过程。这里采用有限元法对整个开挖卸载过程进行模拟，并对卸载过程中围岩变形特征进行分析和研究。

为了简化计算并使分析结果不失一般性，仅取套芯应力解除区段进行数值模拟，建立的网格模型如图4所示。数值模型由4部分组成：岩体、拟环切的解除环形槽（环状岩芯）、应变计胶筒（环氧树脂）、胶水层（黏结剂）。取岩体尺寸为700 mm×700 mm×700 mm，测量小孔直径为36 mm，模拟的胶水层厚度为1 mm，被解除岩芯直径设定为130 mm，钻进方向沿z轴负方向。有限元模型网格选用六面体单元进行划分，共划分137 660个单元、192 328个节点。需要指出的是，无论是岩体、应变计胶筒（环氧树脂）还是胶水层（黏结剂），都采用实体单元进行模拟。钻孔应力解除法地应力计算模型是基于线弹性岩石力学理论建立的，本文采用与地应力计算一致的理论模型，材料都采用线弹性本构，具体的力学参数见表1。

图4 有限元网格模型

表1 模型材料力学参数

2.2 边界条件

在有限元模型负z向边界施加法向约束，开挖面为自由面。x向、y向的正向边界分别施加10、5 MPa的均布面力，x向、y向的负向边界施加法向约束。

2.3 应力解除全过程数值模拟研究

根据已建立的有限元模型，为了模拟整个套芯应力解除全过程，共分16个计算步，其中：1～7步每次解除3 cm，8～11步每次解除2 cm，12～16步每次解除3 cm。每个计算步相当于一次“开挖卸荷”，经过16次“开挖卸荷”之后，就实现了对套芯应力解除全过程的模拟。8～11步每次钻进较少，仅开挖2 cm，其目的是为了获得靠近应变片位置附近的围岩变形情况，从而对埋设在测量小孔内的探头所能感知的孔壁变形特征进行更精细的描述。

3 有限元数值模拟结果分析与讨论

3.1 应力解除全过程曲线

有限元数值模拟计算得到的应力解除全过程曲线如图5所示。可以看出，解除深度到达25 cm（感知孔壁变形的应变花所在位置）之前，各应变片的应变值变化较小；此后，各应变片的应变值发生突变并逐渐趋于稳定，这与现场实测的孔壁变形特征相一致［7］，说明有限元计算结果是正确的。

图5 应力解除全过程曲线

在采用空心包体式钻孔应变计进行地应力测量过程中，为了避开大孔孔底局部应力集中的影响，在设计测量探头时需要将应变片布置在应力集中影响区域之外。通过数值模拟分析和研究，在测量小孔孔深与探头长度一致的情况下，建议将应变片布设在测量小孔孔深的黄金分割点附近。

3.2 修正系数取值对地应力计算结果的影响

为了分析修正系数取值对地应力测量精度的影响，这里假定胶水层与应变计胶筒的材料特性相同，岩体弹性模量和泊松比与2.1节取值相同，应变计胶筒弹性模量E1在3～40 GPa范围内变化，其泊松比μ1＝0.3保持不变，在此条件下分别计算了考虑修正系数和忽略修正系数两种情形下的地应力（见表2，表2分别列出了工程中较为关注的最大主应力σ1的量值、倾角和方位角［19］，以及中间主应力σ2、最小主应力σ3）。对于忽略修正系数的情形，对应于一般三轴孔壁应变计的地应力计算方法［20］，这时修正系数取值为1。

如果以有限元模型中施加的荷载为“真实值”，则由表2可知，考虑修正系数时计算得到的主应力值接近真实值，误差较小；而忽略修正系数时计算得到的主应力值普遍大于真实值，误差与设置的应变计胶筒弹性模量E1有关。为了更直观地进行比较，图6给出了主应力比值（主应力计算值与真实值的比值）与应变计胶筒弹性模量的关系。可见，考虑Kn时主应力比值平稳，说明此时Kn较好地反映了孔壁应变经过介质传递造成的影响。当忽略Kn时，随着应变计胶筒弹性模量E1从3 GPa增大到40 GPa，最大、中间主应力比值从1.276和1.178分别减小至1.072和1.092，说明当应变计胶筒弹性模量与岩体弹性模量接近时，计算中忽略Kn造成的误差越小。

表2 考虑与忽略修正系数时地应力计算结果

图6 主应力比值与应变计胶筒弹性模量的关系

3.3 胶水层材料特性对地应力的影响

前面的分析中都假定胶水层与应变计胶筒材料性能一致，但在实际应用过程中很难做到二者性质完全相同，这里就此问题进行简要分析和讨论。设定岩体弹性模量E＝40 GPa、泊松比μ＝0.2，应变计胶筒弹性模量E1＝5 GPa、泊松比μ1＝0.3。除了前述边界条件不变外，z向的负向边界施加3 MPa的均布面力。

3.3.1 胶水层弹性模量E2对地应力的影响

设定胶水层泊松比不变，其弹性模量E2从1 GPa变化到30 GPa，地应力计算结果见表3，主应力比值与胶水层弹性模量的关系如图7所示。

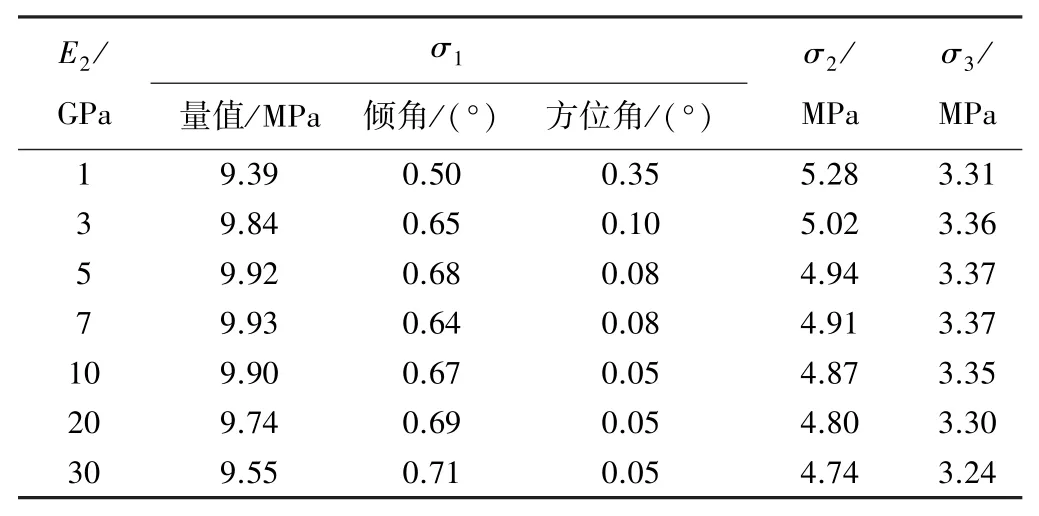
表3 不同胶水层弹性模量下地应力计算结果

图7 主应力比值与胶水层弹性模量的关系

可以看出，随着胶水层弹性模量E2从1 GPa增大到30 GPa，最大、最小主应力比值均呈先增大后减小的趋势，而中间主应力比值呈逐渐减小的趋势。σ1、σ2与真实值之间差值较小，最大误差分别为6.1%和5.6%；σ3显著大于真实值，误差在8.0%～12.3%之间，这也印证了白世伟等［21］关于空心包体法测量地应力结果会导致轴向应力偏大的结论。

3.3.2 胶水层泊松比μ2对地应力的影响

设定胶水层弹性模量E2＝5 GPa不变，其泊松比μ2从0.2增大到0.4，地应力计算结果见表4，主应力比值与胶水层泊松比的关系如图8所示。

表4 不同胶水层泊松比下地应力计算结果

图8 主应力比值与胶水层泊松比的关系

由图8可知，最大、中间、最小主应力比值都随μ2的增大而增大。当μ2从0.2增大到0.4时，σ1、σ2及σ3的误差分别从－1.5%变化至0.3%、3.0%变化至1.2%、11.3%变化至14.0%，σ3的误差相对较大，并且在μ2较小时误差相对较小。

4 工程实例分析

以三峡工程船闸区的地应力分析为例。刘允芳等采用空心包体式钻孔应变计在三峡工程船闸区进行了多个钻孔的地应力实测［7］，以了解永久船闸开挖对应力场分布的影响。试验钻孔ZK2位于二闸室，钻孔高程与闸室底板高程相当［15］，距离闸室边墙约40 m，钻孔仰角为5°，方位角为201°。钻孔ZK2位置如图9所示［7］。

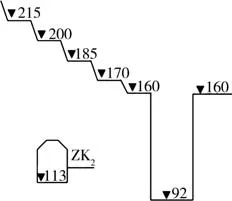
图9 ZK2钻孔位置示意（单位：m）

地应力测试孔直径为130 mm，测量小孔直径为36 mm，测点距孔口约8.15 m，测点埋深为120 m。现场测量采用长江科学院自主研制的空心包体式钻孔应变计，3组应变花的布置极角分别为0°、120°、240°；每组应变花中应变片与轴向的夹角为0°、45°、90°、120°；应变计内径为15.3 mm，应变片嵌固半径为16 mm，应变计胶筒弹性模量E1＝3 GPa、泊松比μ1＝0.36。

测点实测应变值见表5，由围压试验得到的岩体弹性模量E＝55 GPa、泊松比μ＝0.2，计算得修正系数K1＝1.183 6、K2＝1.239 0、K3＝1.114 9、K4＝0.841 7，测点处地应力计算结果见表6。