基于 DMC-PID 双环控制的提升机恒减速制动系统研究

李福勇，齐学海，安传栋

山东能源新矿集团公司 山东泰安 271219

制 动系统的高可靠性是保证提升机安全运行的关键[1]。提升机制动系统安全制动方式主要有两种[2]：恒力矩制动和恒减速制动。由于恒力矩制动过程中制动力不变，提升系统容易在制动力矩过大时受到较大冲击，导致断绳、坠笼等事故。相较于恒力矩制动，恒减速制动过程更加安全平稳，但相应地，矿山企业对其控制系统也有着更高的要求[3]。

国外研制提升机制动系统的厂商主要有瑞典 ABB和德国 SIEMAG。近年来，国内学者针对提升机制动系统的调速及制动性能进行了大量研究[4]。葛明臣等人[5]用滑模控制器代替调速系统转速调节器，有效改善了传统煤矿提升机调速系统响应速度慢、超调大且抖振大的问题。张烨[6]针对传统 PID 控制无法兼顾负载多变、效率低且高故障率的矿井提升机调速系统的快速性和稳定性问题，提出了神经网络 BP-PID 控制算法来提高其调速系统的工作效率和性能，利用 BP网络的自学习，实现传统 PID 控制参数的调整。王利栋等人[7]针对提升机恒减速制动系统超调量较大的问题，提出了一种将模糊 PID 控制与 BP 神经网络相融合的提升机恒减速度控制方法。

目前国内在恒减速制动控制的研究上，控制策略多以传统的 PID 控制方式为主。由于提升机运行工况复杂，在运行过程中有许多变化的因素，因而难以建立精确的传递函数，以保证响应速度和稳态误差。本文提出了一种结合 DMC 与 PID 双环控制制动过程减速度的控制方法，并对控制器进行参数整定，以提高恒减速系统的响应速度和控制精度。

1 恒减速制动过程模型的建立

恒减速制动控制是一个自动控制过程，笔者针对制动系统建立数学模型，并在此基础上设计了恒减速控制系统。

1.1 数学模型

恒减速制动系统由恒减速制动液压通道和恒减速制动机械结构 2 个模块组成，如图 1 所示。

图1 恒减速制动系统的组成Fig.1 Constitution of constant deceleration braking system

比例方向阀接收来自放大电路的控制信号，以改变液压回路通道，使大小相异的压力油流入盘形制动器；压力油与滚筒两端被施加的正压力相对应；利用大小不同的正压力控制滚筒运行的减速度。

放大电路主要对控制信号进行放大，以驱动比例方向阀动作。可以将驱动电路对控制信号的调理看作比例控制环节，即

式中：us为经放大电路放大后作用在比例换向阀两端的信号；ki为放大电路的放大倍数；ui为从控制器发出的信号。

比例方向阀开口大小由其两端控制信号控制。阀口开度xs与控制信号也可近似看作比例控制环节，即

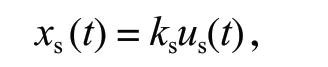
式中：xs(t) 为比例方向阀的开度，其值可取正负，当取值为负时，表示负开口，此时盘形制动器处于泄压状态；ks为比例环节的比例系数。

通过调整比例方向阀的开度，控制制动系统的油压。当xs为正时，对制动器进行充压，即

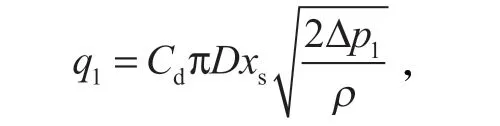
式中：q1为自比例方向阀流出后进入制动器内的液压油流量；Cd为流量系数；D为阀芯台肩直径；Δp1为充压过程中方向阀阀口两端的压差；ρ为液压油密度。

同理，在制动器泄压过程中，有

式中：q2为从制动器流出的液压油流量，与充压过程中不同的是，其值为负；Δp2为泄压过程中流经阀口的压差。

盘形制动器内部的可压缩流体连续方程为

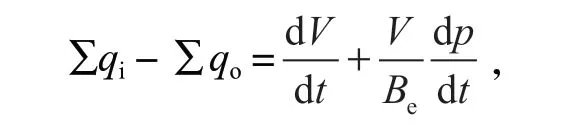
式中：∑qi为流入制动器腔体内液压油流量总和；∑qo为其流出流量总和；V为制动器腔体体积；Be为液体体积弹性模量。

忽略泄漏的影响，则有：

为方便后续分析，做以下两点假设。

(1) 在恒减速制动过程中，制动盘紧贴盘形制动器，液压缸与活塞之间相对位移为零，因而假设液压缸内部体积不变。

(2) 比例方向阀在恒减速制动过程中会不断根据反馈信号调节开口大小，使油压始终在工作点附近呈较小幅度的微调，故阀口两端的压差 Δp1与 Δp2可近似看作常数。记作

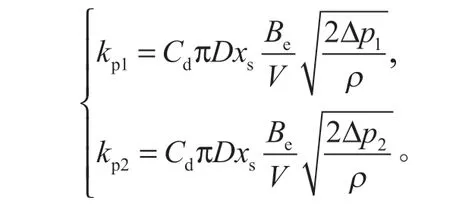
分别可得：

充压过程中，

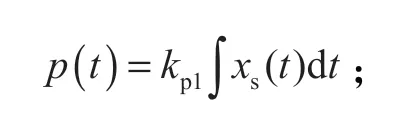
泄压过程中，

由此可知，可将恒减速制动控制回路视为积分环节。假设阀口两侧的压差 Δp1和 Δp2相等，则在充压和泄压两状态下，kp1=kp2=kp，可将p(t) 合为一个公式表达，即

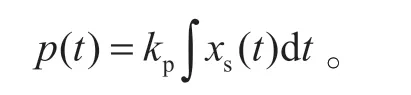
在实际工作过程中，液压通道的输出响应存在一定延迟，将此延时特性看作恒减速通道的纯迟延，用τ表示，则

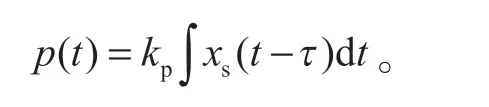
在工作点附近，可将由滚筒和盘形制动器组成的机械结构看作线性定常过程。故可用二阶惯性环节描述此机械结构，即

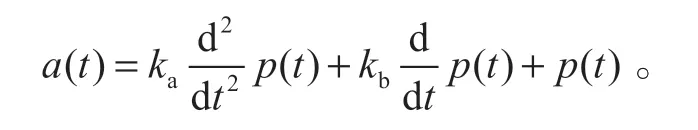
1.2 参数辨识

为了方便辨识过程模型中的参数，将油压控制的3 个环节合并为比例积分加纯迟延环节，其传递函数为

式中：P(s) 为拉氏变换后的p(t)；U(s) 为拉氏变换后的u(t)。

机械结构的传递函数为

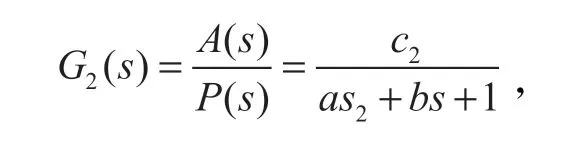
式中：A(s) 为拉氏变换后的a(t)。

上述数学模型为恒减速制动过程中的连续时间模型，其中a、b、c1、c2、τ为待辨识参数。根据采样定理，在对连续时间模型进行采样时，设定采样频率为10 倍的比例阀最高工作频率，即采样频率ωs=1 000 Hz。

将系统延迟记作d，离散后转化为差分方程形式

为了辨识恒减速制动过程数学模型中的参数，搭建试验平台，采集液压制动系统的油压和速度数据。本文中的数据来自新矿集团某矿，包括重载提升和下放两种工况的数据。将其中接近阶跃响应的原始数据导入 MATLAB 软件，并对采集数据进行归零化和中值滤波处理，结果如图 2～ 4 所示。

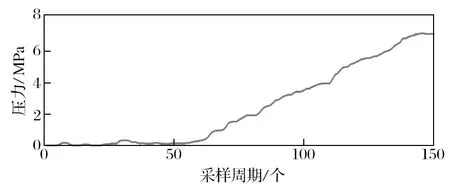
图2 减速液压通道的压力响应曲线Fig.2 Pressure response curve of constant deceleration hydraulic passage

在减速度和压力响应试验中，阶跃信号分别作为油压变化量和比例阀的控制电压信号变化量给入系统。利用递推最小二乘法对模型参数进行辨识，辨识结果如图 5～ 7 所示。模型中未知参数的辨识结果如表 1 所列。

表1 未知参数的辨识结果Tab.1 Identification results of unknown parameters

图3 重载提升工况下制动减速度响应曲线Fig.3 Braking deceleration response curve in heavy-load hoisting mode

图4 重载下放工况下制动减速度响应曲线Fig.4 Braking deceleration response curve in heavy-load lowering mode

图5 恒减速液压通道辨识结果Fig.5 Identification results of constant deceleration hydraulic passage

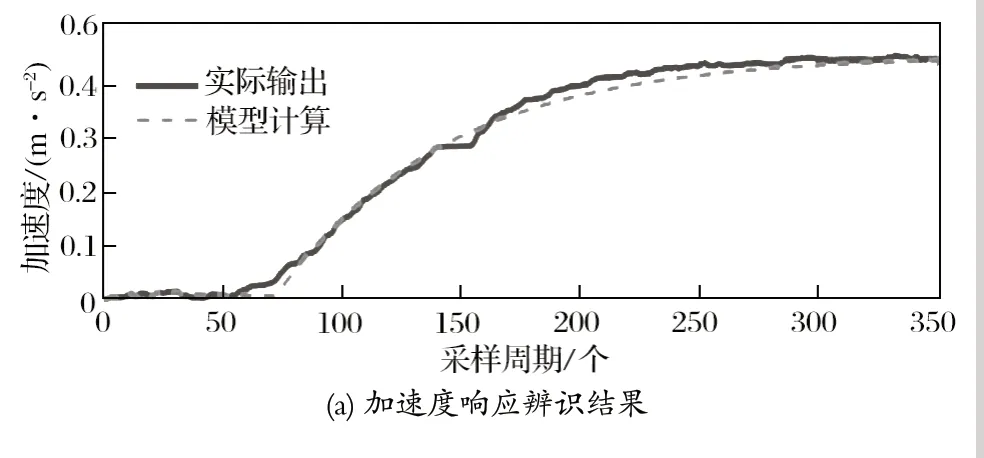
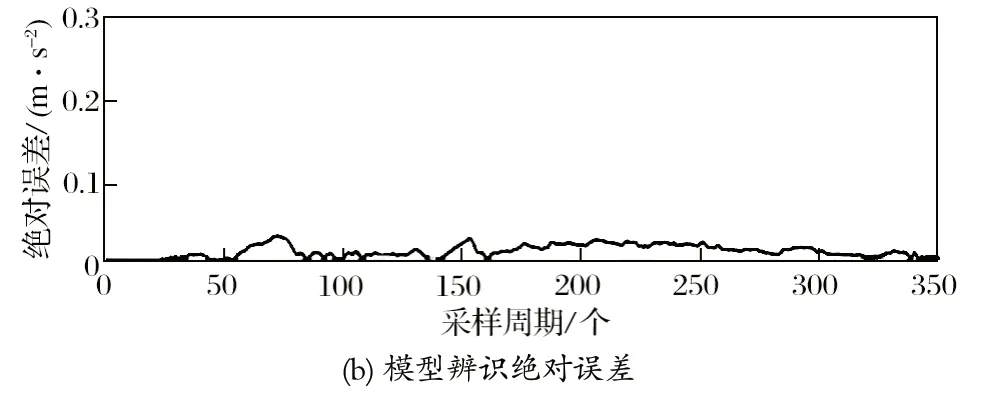
图6 重载提升工况下恒减速制动辨识结果Fig.6 Identification results of constant deceleration braking in heavy-load hoisting mode

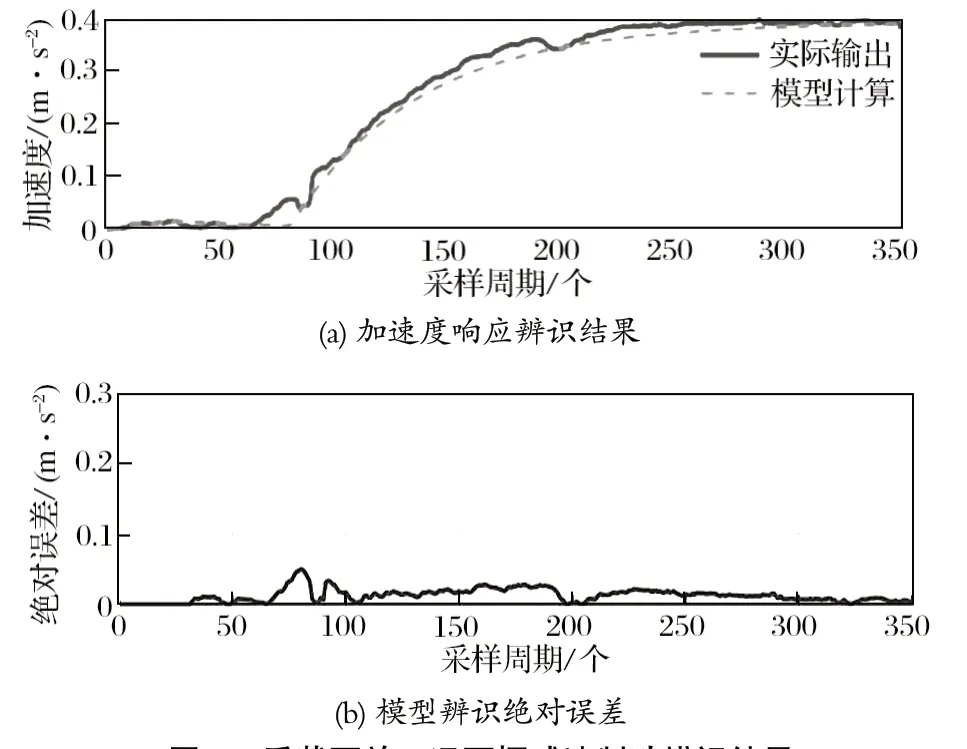
图7 重载下放工况下恒减速制动辨识结果Fig.7 Identification results of constant deceleration braking in heavy-load lowering mode

2 恒减速制动过程控制方法的研究

2.1 控制方案设计

比例方向阀作为流量控制元件，无法直接改变油压，在控制环节中为非渐稳对象。基于此，结合 PID和 DMC 控制策略，设计了恒减速制动双环控制回路。外环主要元件是速度传感器和 DMC 控制器；内环主要由油压传感器、比例阀和 PID 控制器组成，如图 8 所示。

图8 恒减速制动过程控制方案Fig.8 Control scheme of constant deceleration braking process

2.2 DMC 控制器的设计

动态矩阵预测控制算法由控制、预测和校正 3 个部分组成，如图 9 所示，细箭头代表纯量流，粗箭头代表向量流。

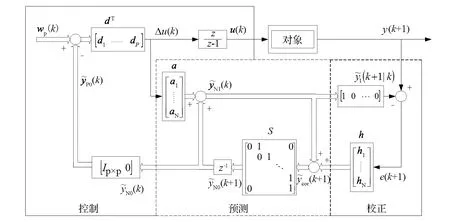
图9 动态矩阵控制算法的原理框图Fig.9 Block diagram of principle of dynamic matrix control algorithm

DMC 算法的三组重要参数可通过以下方法获得：

(1) 由制动系统的单位阶跃响应可确定模型向量{ai}，本文辨识的模型建模时域为N；

(2) 通过计算可得出控制向量 {di}，Q、R、M、P是优化策略的反应参数，其值可通过仿真整定；

(3) 本研究选择单位向量作为校正向量 {hi}。

2.3 DMC-PID 双环控制仿真分析

为验证 DMC-PID 双环控制策略的优越性，在Simulation 中分别搭建了传统 PID 控制和 DMC-PID双环控制下的恒减速制动系统，并针对提升和下放两种工况下的减速度响应曲线进行对比分析。

2.3.1 传统 PID 控制

本研究的制动策略应用在倾角θ为 6°的斜井提升系统中。根据《煤矿安全规程》规定进行计算，当倾角θ为 6°时，提升减速度不能大于 1.47 m/s2，下放减速度不能小于 0.75 m/s2，因而仿真时将减速度设置为 1.00 m/s2。传统 PID 控制仿真参数如表 2 所列，仿真结果如图 10、11 所示。

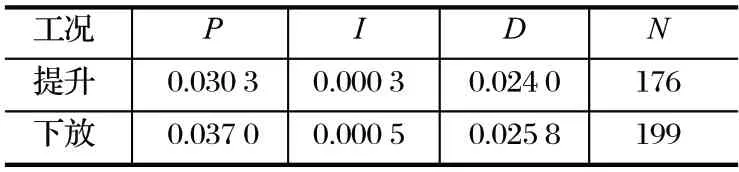
表2 传统 PID 控制参数Tab.2 Parameters of traditional PID control

图10 提升工况下传统 PID 控制仿真结果Fig.10 Simulation results of traditional PID control in hoisting mode

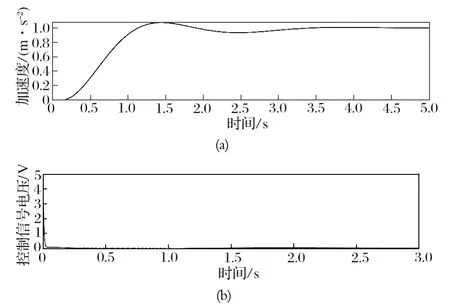
图11 下放工况下传统 PID 控制仿真结果Fig.11 Simulation results of traditional PID control in lowering mode

由图 10、11 可知：传统 PID 控制可以实现在两种工况下制动过程的减速度稳定，但减速度曲线存在波动；当设置预期减速度值为 1.00 m/s2时，提升和下放两种工况下减速度稳定所需时长分别为 3.71 和3.47 s。

2.3.2 DMC-PID 双环控制

在 DMC-PID 双环控制策略下，仿真所需参数如表 3 所列。提升和下放两工况下，仿真结果分别如图12、13 所示。

表3 DMC-PID 双环控制参数Tab.3 Parameters of DMC-PID dorble-loop control

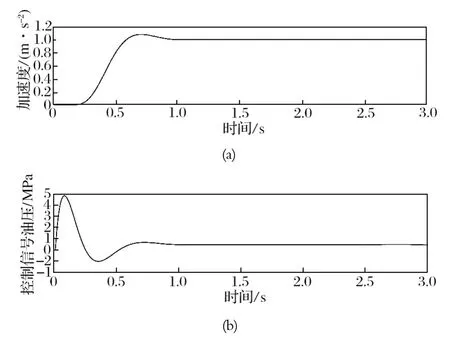
图12 提升工况 DMC-PID 双环控制仿真结果Fig.12 Simulation results of DMC-PID double-loop control in hoisting mode

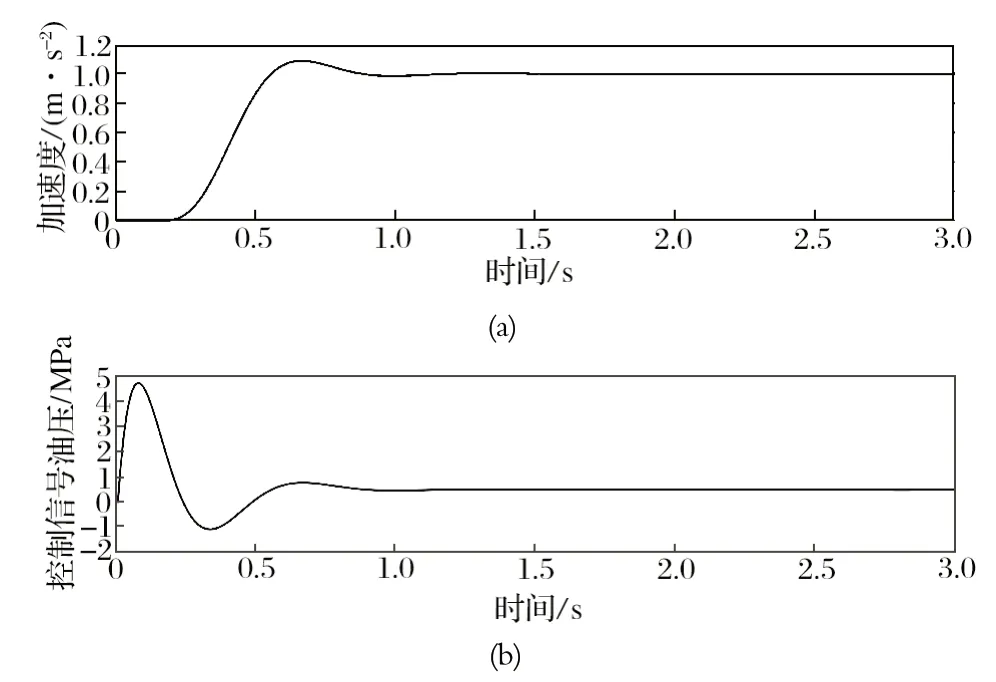
图13 下放工况 DMC-PID 双环控制仿真结果Fig.13 Simulation results of DMC-PID double-loop control in lowering mode

由图 12、13 可知：采用 DMC-PID 双环控制策略，提升和下放过程中的减速度分别在 0.81 和 0.77 s时后稳定在了 1.00 m/s2，并在此后波动幅度始终小于5%。

传统 PID 控制与 DMC-PID 双环控制的性能对比如表 4 所列。

表4 两种控制策略的性能对比Tab.4 Comparison of two kinds of control strategy in performance

由表 4 可知，在提升机恒减速制动过程中，相较于传统 PID 控制，采用 DMC-PID 双环控制策略，减速度控制更加平稳，响应更加迅速。

3 结语

针对现阶段矿山提升制动系统无法较好满足变载荷、高速重载、控制对象不确定等问题，提出了基于 DMC 动态矩阵与 PID 控制结合的控制方案，并在Simulation 中分别搭建了传统 PID 控制和 DMC-PID双环控制下的恒减速制动系统，针对提升和下放两种工况下的减速度响应曲线进行仿真分析。结果表明：相较于传统 PID 控制，DMC-PID 双环控制可得到更好的控制效果。这为进一步研究并提高提升机恒减速制动控制系统的性能提供了参考。