基于电流畸变的配网单相接地故障选线与判别＊

汪胜和,陈晓东,项忠华,叶远波

（1．国网安徽省电力有限公司，安徽 合肥 230022；2．国网安徽省宣城供电公司，安徽 宣城 242000）

1 引言

随着新能源在电网的渗透率不断增高，配电网逐渐成为多源网络，配电网单向接地故障检测和定位变得更为复杂。现阶段电网需要进行同步量测实现广域运行电网的实时状态监测，配电网单向接地故障检测如利用相应电压电流的关系，则可以解决实时故障、定位等问题。

目前针对小电流接地系统的单向接地故障、选线主要分为稳态法、暂态法和主动法[1]。稳态法主要使用稳态信号进行故障判别；暂态法是主要基于小波分析而提取子频带内暂态连续电流信号的方法；主动法是需要利用消弧线圈或电力电子装置向配电网注入不同频率的信号来检测故障线路。目前这类方法中，暂态信号方法具有较高的准确率，而人工智能方法具有较大的不确定性。

目前针对单相接地故障的检测研究较多。文献[2]提出了考虑配电网分布式零序电流关系的单相接地故障定位。文献[3]提出了一种配电网馈出线路单相永久性接地故障性质辨识方法。文献[4]针对谐振接地系统单相接地故障有源电流注入全补偿消弧进行了研究。文献[5]提出了一种基于同步量测大数据的配网单相接地故障检测及定位方法。文献[6-8]提出了一种基于卷积神经网络的配电网单相接地故障识别方法。文献[9]提出了含分布式电源的配电网单相接地故障精确定位方法。这些研究都较为复杂，求解难度较大。本文针对单相接地故障短路故障诊断进行了分析，提出了一种针对电流畸变的单向接地故障诊断方法。首先建立了配网单向接地故障的模型，分析了故障向量图。提出了基于凯伦布尔变换的单向接地故障判断方法。利用健全相和故障相之间电流畸变的关系判断故障线路。针对所提的模型进行的仿真分析，进而说明了本文所提方法的有效性。

2 配网单相接地故障模型

配电网一般为小电阻接地或消弧线圈接地系统，当系统发生单相接地故障时，系统的暂态电容电流主要由故障相电压降低引起的电容放电以及非故障相电压升高引起的电容充电过程组成。

在配网单相接地故障线路选线过程中，继电保护装置需要识别各种物理量的变化，主要是基于电压和电流量的变化。由于在正常运行时系统为三相对称系统，不存在零序分量；一旦发生单相接地故障，则会产生零序分量。系统继电保护装置，可以利用这一分量对系统故障线路进行判断。但是由于在小电流接地系统中连续分量变化在某些情况下感知程度不够，难以判断具体故障线路。在负荷相电流以及大地与线路电容之间的电流形成的总电流导致配网环流，从而干扰了系统继电保护装置对故障线路的判断和检测。

图1给出了单相接地故障的零序网络图。一般情况下，非故障线路两侧的故障电流和故障分量电流基本相等，而故障线路两侧的故障电流和故障分量电流一般不等，距离故障点最近的支路故障电流最大，针对单相接地故障通常利用零序电流进行分析。

针对零序电流，有下列表达式：

其中ωdch为放电频率分量，与网络形式、长度、故障点到保护装置的距离有关。；ωch为充电频率分量，取决于网络电容电流以及电源阻抗。

系统正常状态时，各馈线的对地电容电流计算如下：

当L1发生单相接地故障，非故障相五次谐波电流为：

非故障相的各次谐波突变量计算如下：

相应的向量图分析如图2、图3所示。

上述分析主要针对中性点不接地系统，对于中性点接地系统，分类方法类似。

3 基于凯伦布尔变换的单相接地故障模型

3.1 凯伦布尔变换

凯伦布尔变换适用于三相系统的解耦分析，主要应用于暂态分析。其原理如下所示：

其中，T-1为变换矩阵；Xp为相分量矩阵；

由基本电路关系，得到：

其中，考虑系统对称，

其中，Z0、Z1和Z2为网络阻抗的0，1，2 模。上述变换不涉及复数，求解较为方便，因此，可以将三相系统用该方法进行解耦。

考虑图1的中性点不接地系统发生的单相接地故障，三相对称为系统，系统等值阻抗由线路、变压器和负荷构成，得到Zeq。

对于某一线路f处发生单相（a）接地故障，边界条件为：

由卡伦布尔变换，得到相对模的变换结果：

其中，U0、U1、U2和I0、I1、I2分别为电压和电流模相量。

则故障电压表达式为：

各种故障条件下的特征量如图4所示[8]。

3.2 单相接地故障判断方法

当系统出现稳态故障时，故障电流为正弦量，表达式如下：

为简化分析，考虑如下关系：

其中，φ为故障时初始相角。

为实现甄别健全相和故障相，考虑相电流畸变率：

选相的判别标准为，单相接地故障线路中的健全相e＜0，故障相e＞0。

4 单相接地故障定位流程

本文所提的基于电流畸变故障判断方法流程图如图5所示。

对故障后的三相电流进行凯伦布尔变换，可以得到相应的模故障分量。这类故障分量含有一定谐波，需要进行相应的谐波处理。然后利用电流畸变方法确定畸变率的大小。进而进行故障线路的判断。

5 算例分析

5.1 系统说明

本文选取某系统进行仿真分析，仿真环境为MATLAB2012b，接线图如下图6所示。

线路的长度和参数如下表所示。

表1 线路长度

架空线参数为：r1=0．1471Ω/km，l1=0．43Ω/km，c1=0．0093μF/km，r0=0．5144Ω/km，l0=1．3885Ω/km，c0=0．006μF/km。

电缆参数为：r1=0．196Ω/km，l1=0．102Ω/km，c1=0．26μF/km，r0=1．96Ω/km，l0=0．34Ω/km，c0=0．158μF/km。

5.2 算例分析

故障线路零序电流在42ms时的波形如图7所示：

可以看出，在故障发生后的极短时间内，故障相电流经历很短暂的暂态波动，这与系统的过阻尼或欠阻尼形式有关，之后便逐渐进入稳态故障状态。

在暂态过程持续一定时间后，大约30ms后进入稳态过程，利用本文所提谐波畸变方法进行故障判断。

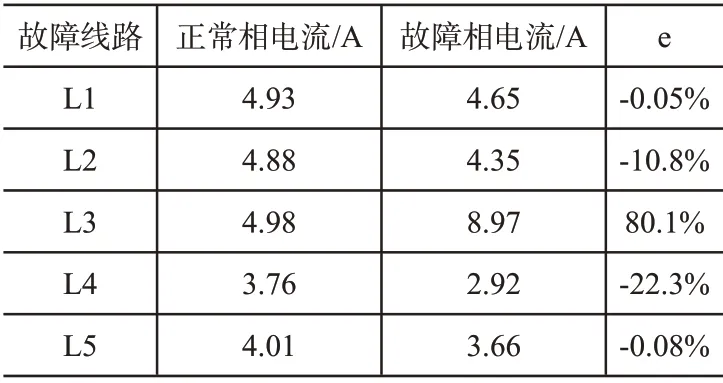
表2 电流畸变率计算结果

可以看出，仅故障相的畸变率为正，即电流增大。另外为了验证本文所提方法的有效性，对故障的线路、初始角、接地电阻和故障位置均进行测试，得到的结果如表3所示。

表3 故障选线结果

6 结束语

本文提出了一种基于电流畸变的单相接地故障诊断与定位方法。首先分析了单相接地故障时的相电流分量关系。然后说明了凯伦布尔变换原理，建立了基于该变换的单相接地短路故障分析模型。提出了稳态故障下的相电流畸变方法，说明了选线原理和流程。

仿真算例表明，针对不同的故障条件，本文方法选线结果均正确，由此可见，本文所提方法针对不同的故障条件均显示出了较高的可靠性。