大型空间异形钢塔斜拉桥拉索张拉控制
2022-11-26李鹏飞王石磊魏思聪罗吉庆
李鹏飞,王石磊,魏思聪,李 毅,罗吉庆
(1.交通运输部公路科学研究所,北京 100088;2.中国铁道科学研究院集团有限公司,北京 100081;3.广东省公路建设有限公司,广东 东莞 510660)
0 引言
某大桥采用五跨高低双塔斜拉刚构连续梁桥组合体系,全长639 m,主跨 280 m。主梁采用分离式全焊接钢箱梁。钢塔采用双肢非一致倾斜、空间不对称扭转的变截面全焊接钢箱拱,高塔高123.78 m,高塔处塔梁墩固结,矮塔处塔梁固结,塔底设纵向活动支座。斜拉索采用竖琴式渐变距离布置,塔上索间距2.90~7.26 m,梁上索间距3.76~14.4 m,全桥共计112根拉索,高塔设置68根,矮塔设置44根。高塔中跨34根拉索采用φ7—151型平行钢丝拉索,拉索锚点距介于30~238 m之间,剩余78根拉索采用φ7—139型平行钢丝拉索,拉索锚点距介于24~154 m之间。拉索塔内为锚固端,梁内为张拉端。大桥总体布置如图1所示。
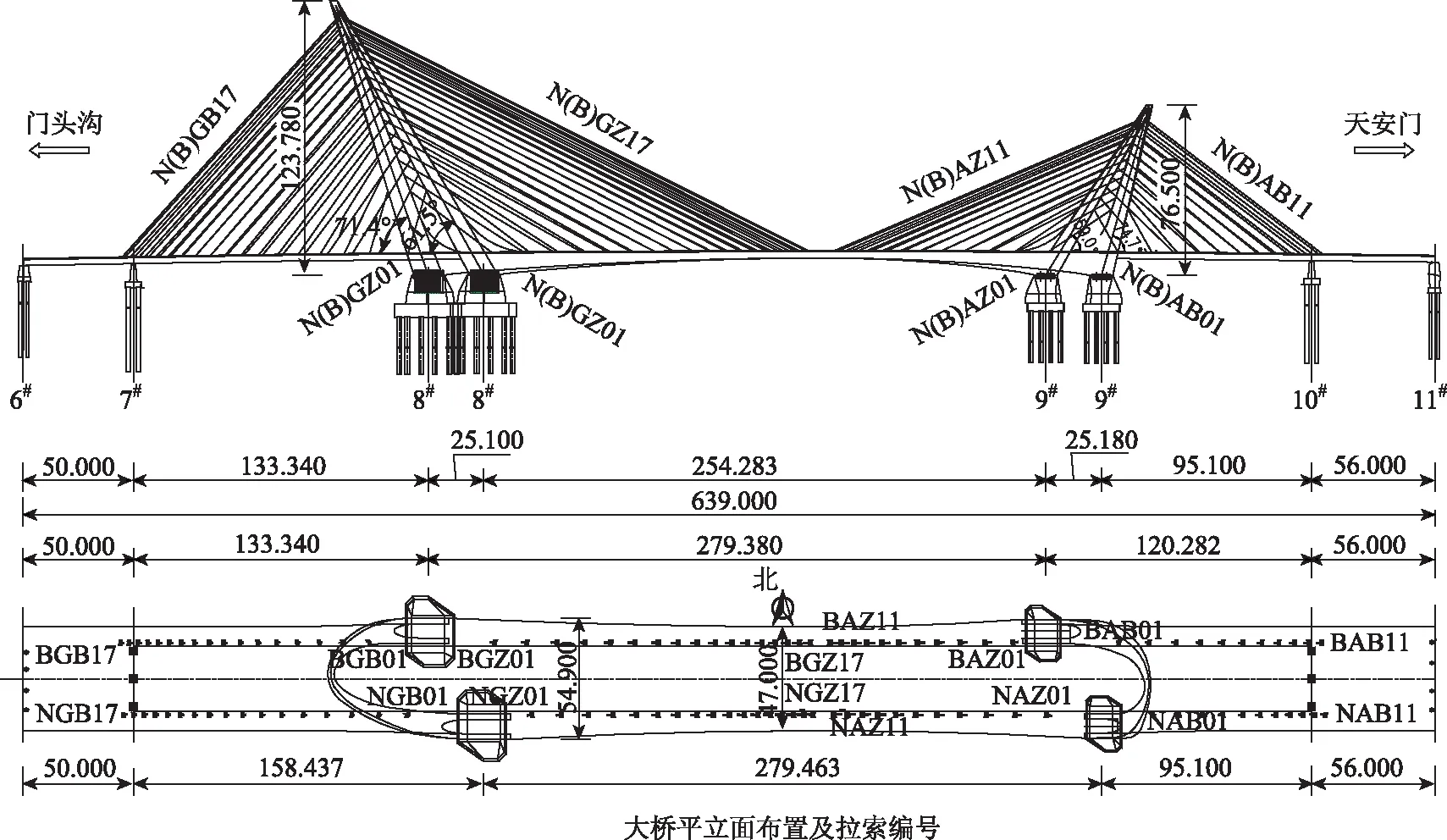
图1 大桥平立面布置 (单位:m)
大桥钢塔及钢梁采用长内节段制造方式,考虑运输、加工及安装起重能力等因素,高塔共计31个节段,矮塔共计21个节段,南北主梁分别划分34个节段。塔梁现场架设整体基于支架辅助安装法。索塔采用弱支架方式安装,自重主要由塔身强度承担,支架提供拼装过程中的临时支撑力,同时为索塔线形调整提供反力支撑,在塔顶设置合龙段。主梁采用强支架方式架设,在高矮塔边跨侧塔根处及中跨高矮塔拉索分界线处设置合龙段。
该桥钢塔空间呈“迈步”扭曲造型,三维变形特征突出,主梁中跨与边跨刚度差异明显,结构受力高度不对称,不同拉索张拉行为相互印证性差,拉索张拉过程中塔梁与支架接触状态及其演变进程难以精准模拟[1-2],传统以力为主要控制目标的施张方法存在诸多不便[3-4],为确保大桥成桥索力符合预期状态,采用无应力状态控制法对拉索张拉进行控制[5-6]。利用有限元法建立大桥全过程仿真计算模型,塔、梁、支架采用梁单元模拟;拉索采用索单元模拟;高塔及支架根部固结,矮塔根采用刚臂与支座、砂箱、锚拉杆连接。塔梁与支架间约束竖向位移,按塔、梁制造节段划分情况设置塔、梁单元;按桥梁设计成型设置节点坐标,建立施工阶段模拟架设步序,将成桥设计索力设置为拉索初张力,获取最终成桥状态,以此为基础计算各拉索无应力索长,后续索力调整通过在模型中调整无应力索长的方式实现。
考虑索塔偏位和活载预拱度计算无应力索长,在初次张拉过程中基于锚头拔出量进行控制,并获取频率与索力的线性标定公式,结合初次张拉索力偏差分析,通过对非施调索调幅进行锁定,基于索力整体影响矩阵和二次型规划优化方法计算了施调索调幅,并建立调幅与锚头拔出量修正值转换关系,采取修改无应力索长方式实现了二次调索。
1 拉索张拉控制流程
大桥主要施工步序为:支架上逐节段拼装钢塔(自塔根同步向两侧架设主梁)→高矮塔合龙→剩余主梁节段架设(同步拆除索塔支架)→高矮塔边跨主梁合龙→中跨主梁合龙→拉索初次张拉→主梁支架拆除→二次调索→施作桥面铺装及附属设施。在中跨合龙前,矮塔根部临时固结,合龙后固结措施予以解除。结合大桥建造方案,拉索张拉控制主要体现在以下3个方面:(1)在制造阶段需计算无应力索长,并结合锚固构造对索长调整范围进行复核。(2)在塔梁合龙结构体系完成转换后,对位于支架上的结构进行初次张拉控制,建立频率与索力标定关系。(3)主梁支架拆除后,通过索力识别及偏差分析,提出索力优化调整控制方法,实现二次调索。拉索张拉控制流程见图2。
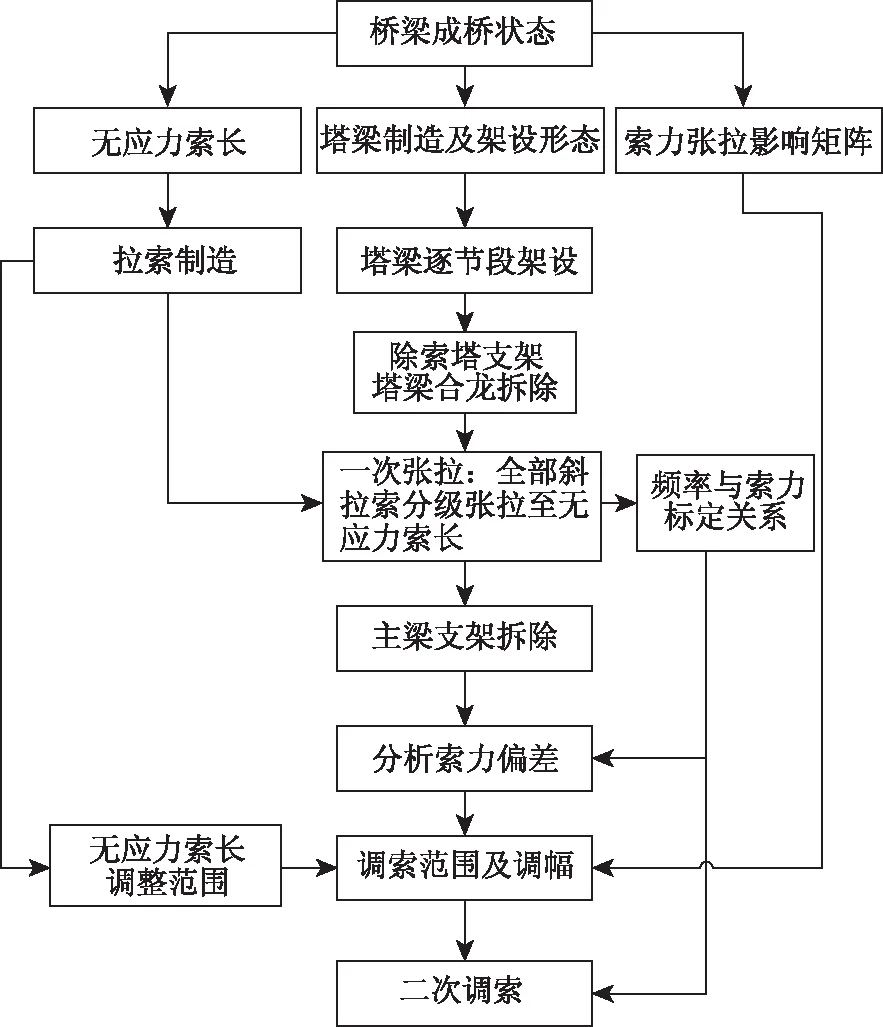
图2 斜拉索张拉控制流程
2 拉索制造及初次张拉控制
2.1 拉索无应力长度计算
拉索无应力长度是施工控制中重要的一项指标,长度偏短将导致有效锚固长度不足或无法锚固,长度偏长将导致张拉力难以到位或者需要增加额外的垫板。对于中等跨径斜拉桥,研究及实践表明基于Ernst 简化理论采用式(1)确定无应力索长完全能够满足精度要求[7-8]。但传统规则斜拉桥无应力索长计算存在问题为:(1)按塔直梁平方式确定理想目标状态的规则斜拉桥,不考虑索塔偏位的影响。(2)按照设计成桥线形进行计算无应力索时,未考虑主梁车道荷载预拱度的影响。未考虑上述两种因素将会导致成品索长存在偏差,对基于无应力状态法进行拉索张拉控制带来较大困难。
(1)
式中,S0为锚固点间无应力索长;T为张拉索力;A为拉索面积;E为拉索弹性模量;q为拉索自重集度;l0为结构变形后锚点间距;l为l0水平投影距离。
基于采用Midas/civil2018对大桥建立有限元模型,塔、梁、支架采用梁单元模拟,拉索采用索单元模拟,高塔及支架根部固结,矮塔根采用刚臂与支座、砂箱、锚拉杆连接,塔梁与支架间约束竖向位移,模型如图3。首先按照施工步序进行全过程施工仿真,基于切线位移法获取塔梁制造及架设几何形态控制数据[9-10],基于理想成桥状态开展车辆活载分析,计算车道荷载主梁预拱度值,按照式(2)计算变形后锚点间距l0并代入式(1)计算无应力索长。大桥中跨计算车道荷载预拱度为150 mm,高塔成形偏位为78 mm,可见若忽略该因素的影响将会对无应力索长带来较大偏差。
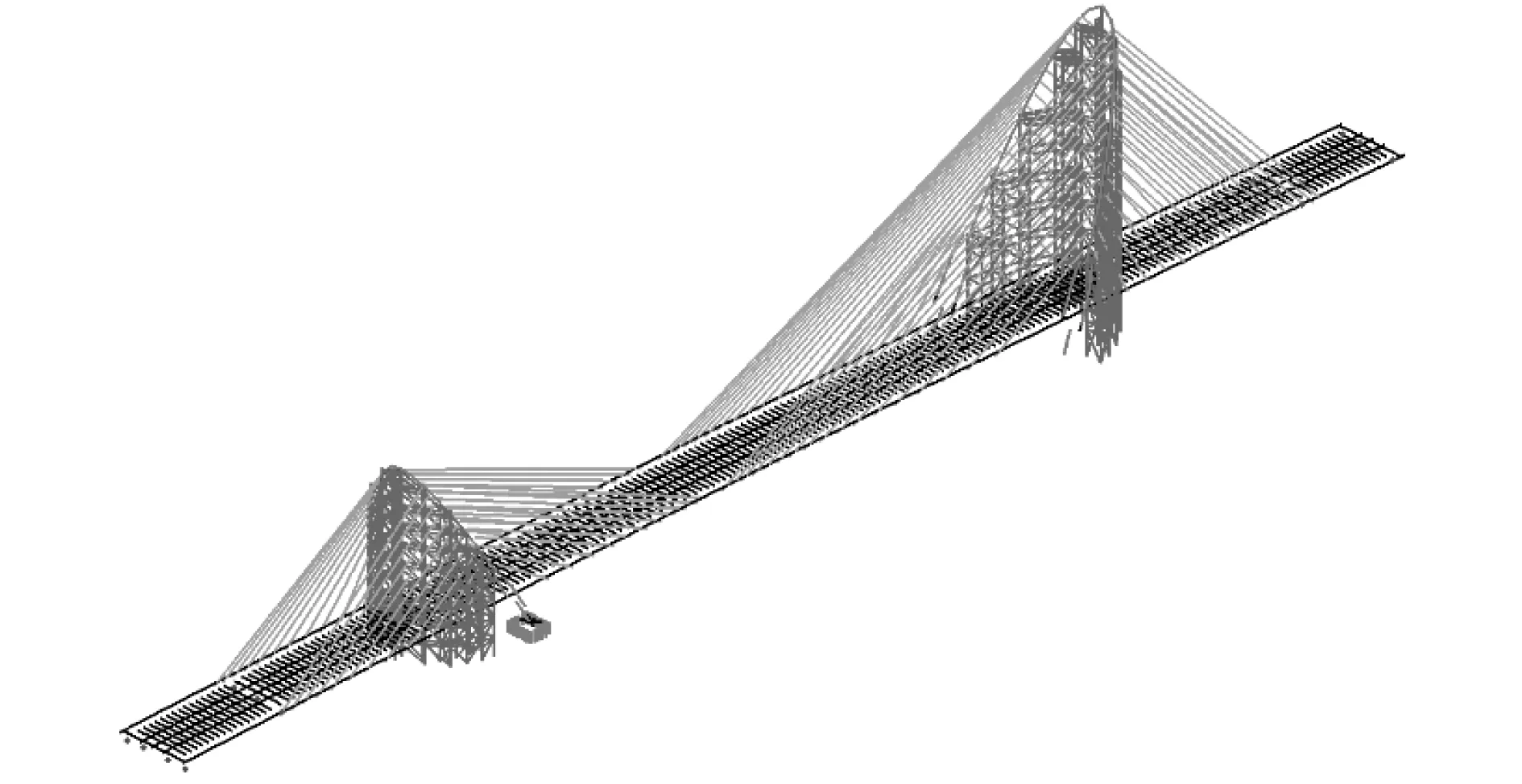
图3 桥梁有限元模型
l0=norm([Xc,Yc,Zc]b+[XHE,YHE,ZHE]b-
[XD0,YD0,ZD0]b-[Xc,Yc,Zc]e-
[XHE,YHE,ZHE]e-[XD0,YD0,ZD0]e),
(2)
式中,X,Y,Z标识拉索锚固点坐标或坐标修正量;b为标识拉索首节点位置;e为标识尾节点位置;c为标识基准状态;HE为标识架设几何形态修正量(对应于架设几何形态修正值);D0为标识大桥竣工状态恒载作用下的拉索首尾节点变形量,部分符号示意如图4所示。
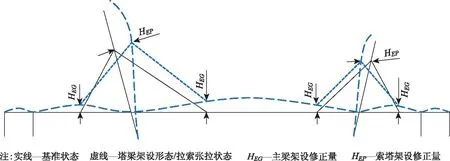
图4 无应力索长计算符号说明
S0计算完毕后需结合拉索锚固构造计算下料长度[11],同时对无应力索长可调节量(张拉端螺母调节范围)进行核算[12],大桥139型拉索无应力索长调节量为-115~170 mm,151型调节量为-124~181 mm,若为正值,则拔出量需减少,对应为退张,若为负值,则拔出量增加,对应继续施张。
2.2 拉索初次张拉及索力标定
塔梁在支架上合龙完成结构体系转换后,进行拉索一次张拉,拉索施张伴随塔梁逐渐脱离支架,结构边界条件存在动态变化,鉴于塔梁与支架接触状态及其演变进程难以精准模拟,传统以力为主要控制目标的施张方法存在诸多不便,背景桥梁拉索一次张拉基于无应力状态法开展,全桥共设8套张拉设备,以分肢塔根为中心顺桥向由近及远、竖向由低至高施张,发挥无应力状态法不同工序并行作业优势[13],中跨及矮塔边跨拉索按无偏差锚头拔出量80%,90%和100%分3级张拉到位。因高塔边跨临时荷载密集,按无偏差拔出量一次张拉到位锚固力大于设计成桥索力,为确保结构安全,拉索按成桥设计索力70%,85%和100%分3级张拉到位。各级张拉完毕后记录千斤顶油压换算索力,同时锤击激振法采集拉索振动基频,为后续索力识别提供依据。研究表明因索端边界条件、抗弯刚度、垂度等因素影响,频率与索力之间存在复杂的非线性关系,部分方程为超越方程,需要迭代计算方可求解[14-15],工程应用存在较大不便,同时实践及仿真分析发现,通过实测频率标定已知索力建立频率索力关系式的方法,能够满足拉索张拉索力控制精度需求[16-19],本研究采取线性公式获取频率平方与索力之间关系,如式(3)所示。
(3)
公式前半部分系数a体现拉索长度、线质量等因素,与传统频谱法计算索力公式不同,后半部分引入系数b,以体现抗弯刚度、边界条件等因素影响。式中,T(f)为索力;fn为拉索n阶频率;系数a,b可基于不少于3次的实测频率与索力线性回归求得。
本研究139型拉索长径比介于291~1 847之间,151型拉索长径比介于358~2 767之间,均大于100,属于长索[20]。基于3级张拉数据,获取每根拉索频率与索力线性标定系数a,b分布如图5所示,相关系数R2分布如图6所示。R2最小值为0.982 2,94%的拉索R2介于0.990 0~1.000 0之间,可见频率平方与索力之间呈现极强线性相关性。同时值得注意的是系数b介于-590~373 kN之间,在不同长度拉索之间离散性较大,以一次张拉为例,其对索力贡献最大可达29%。若忽略该部分影响,仅采用传统频谱法计算索力公式(即公式前半部分)将导致不可忽视的误差。
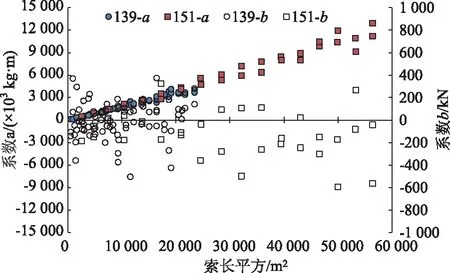
图5 标定系数分布
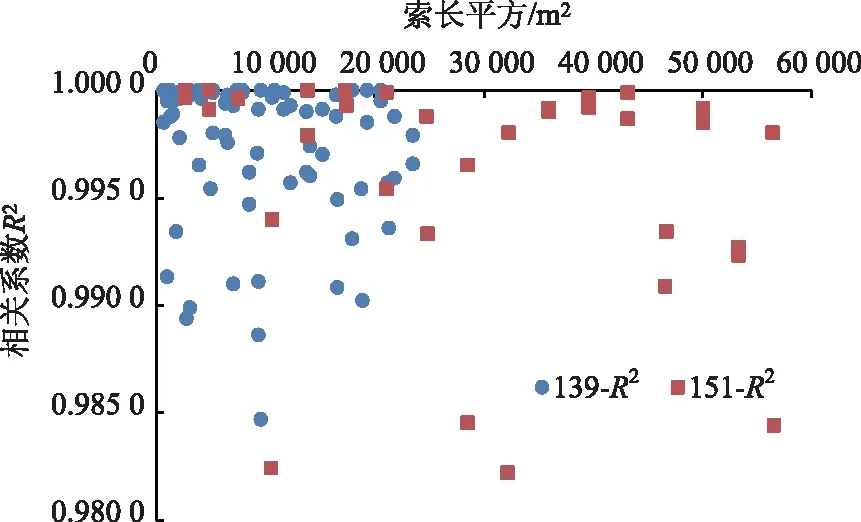
图6 线性标定相关系数
为验证基于一次张拉所获取标定公式的可靠性,在二次调索过程中对49根需要施调的拉索逐根对比张拉前频率推定索力与张拉过程锚固螺母松动油压推算索力,二者偏差分布见图7,最大偏差为6%,90%的拉索偏差在5%以内,可见通过实测频率线性标定已知索力的方法,能够满足索力控制精度需求。
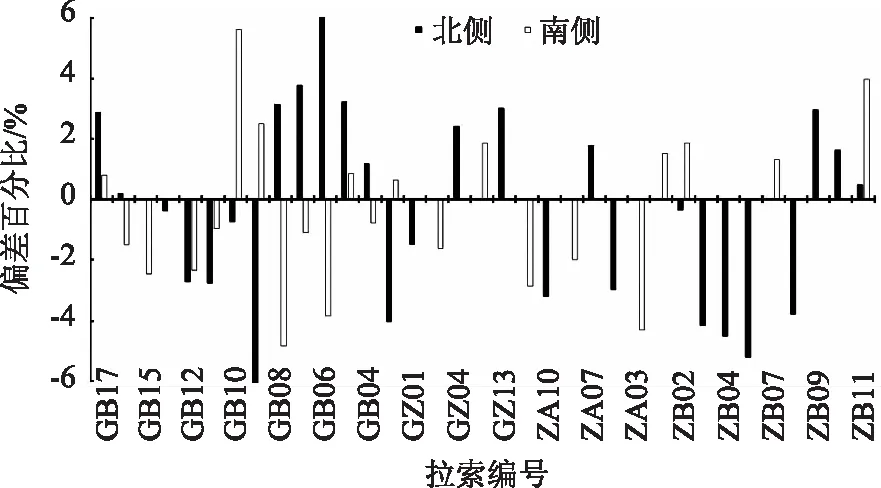
图7 频率法推定索力与实测索力相对偏差分布
3 二次调索控制
3.1 二次型规划优化方法
初次张拉完毕后对拉索索力进行通测,相对于二恒作用前目标索力偏差分布见图8,按无应力索长一次张拉到位的78根拉索中21根偏差大于10%,张拉控制效果良好;未按无应力索长张拉控制的高塔边跨34根拉索中21根偏差大于10%,偏差比率较高。构件制造几何形态(如锚箱定位精度)及节段架设偏差是导致按无应力索长控制的部分索力存在偏离的主要原因,因此在初次张拉完毕确定索力和线形偏差后,需对索力进行二次调整,索力调整的实质在于找出一组斜拉索力使得某种反映大桥性能的目标达到最优[21]。大桥二次索力调整优化采用二次型规划方法。常见优化问题若目标函数可转换为二次实函数,边界可转换为线性约束,则可采用二次型规划方法进行求解,该方法是求解非线性规划问题的一种重要途径[22],一般二次型规划问题的数学表达见式(4)。
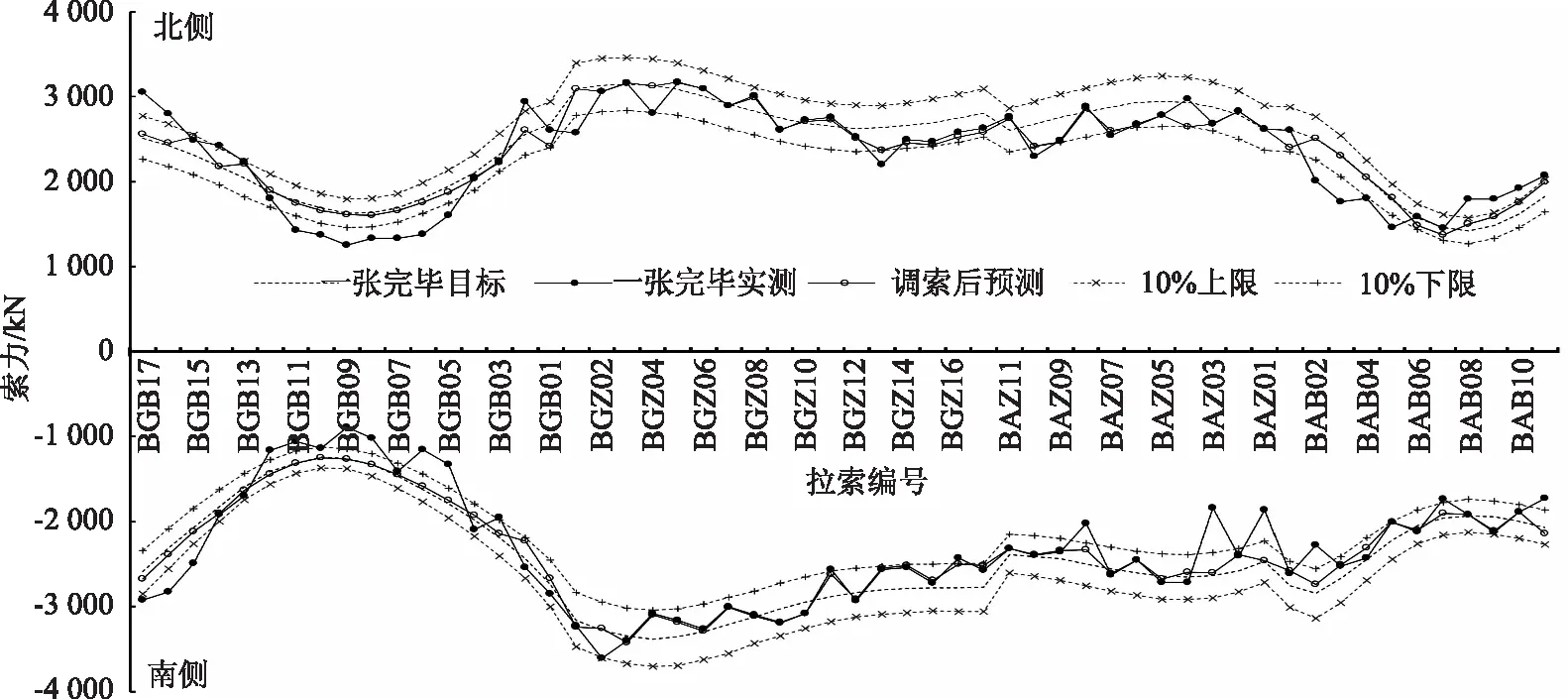
图8 初次张拉完毕后索力分布
(4)
式中,x为决策变量;H为对称矩阵;fT为行向量;A为矩阵;B为列向量;Lb为决策变量下限,Ub为决策变量上限。
设拉索整体数目为n,如式(5)所示,Ft,F0分别为所有拉索目标和当前索力值;D=F0-Ft, 为当前索力相对目标索力差值;Δt为每根拉索调幅。如式(6)所示,C为拉索整体影响矩阵;第i行为每根拉索张拉单位力对第i根索索力影响值;第j列为第j根拉索张拉单位力对每根索索力影响值。通过影响矩阵建立调幅与索力变化的关系,如式(7)所示,按照所有拉索调整后索力相对目标索力偏差的百分比和最小构造目标优化函数。
Ft=[Ft1,…,Fti,…,Ftn]T,
F0=[F01,…,F0i,…,F0n]T,
Δt=[Δ1,…,Δi,…,Δj,…,Δn]T,
(5)
(6)
(7)
对式(7)进行展开,如式(8),因Di为定值,则可对其转换成标准的二次型公式目标函数,各参数取值见式(9)。
(8)
(9)
编制循环程序,即可求得[H]及fT。标准型中Ax≤B在调索中的具有应用在于设置经调幅Δ作用后各拉索力达到指定的上下限,具体设置见式(10),其中α为调索后各索力相对设计索力偏差的百分比限值,城市斜拉桥无规范明确给出其具体数值,一般需与设计共同商定,本研究α=10%。
A=[C,-C],B=[(1+α)Ft-F0;
-(1-α)Ft+F0]。
(10)
因影响矩阵C为满秩n阶方阵,若全部拉索均可调整,则f(Δ)存在为0的唯一解,即Δ=C-1D,无需通过二次型规划求解Δ。事实上,因初次张拉后大部分拉索索力已达到目标状态,仅需选择部分索力偏差尚不满足要求的拉索(受调索,同时为施调索)及其临近索(施调索)进行调整即可实现二次调索,即存在受调索与施调索数目不一致的情况,此时即可按照二次型规划方法完成调索。基于拉索整体影响矩阵实现仅对施调索调整的方法为限制决策变量中非施调索的调整空间,如式(11)所示,设i拉索为非施调索,锁定该决策变量调整空间,令Ubi=0。设j拉索为施调索,释放该决策变量调整空间,令Ubj=β,β为结合单位力大小而设置的一个合理大值。决策变量下限可设为Lb=-Ub。虽然锁定了非施调索调整空间,但目标函数仍能体现调索对全部拉索索力影响。
Ub=[…,Ubi=0,…,Ubj,…]T。
(11)
二次型规划方法求解可基于Lemke方法进行编程求解[22],也可以采用数学软件Matlab最优化工具箱Quadprog()函数求解[23],本研究算例基于Matlab数学软件求解。
3.2 施调索调幅计算
基于本研究的二次型规划方法,选取相对二恒作用前目标索力偏差大于10%的拉索及个别临近拉索共计49根拉索进行索力调整。本研究影响矩阵基于单位力为500 kN求得,初次张拉完毕后各拉索相对施工状态斜拉索拉力允许上限偏差139型拉索为4 079 kN,151型拉索为3 209 kN[11],施调索调幅限值β偏安全取为6.41。计算结果见图9,计算调幅介于-0.9~1.7之间,预测调整后相对目标状态拉索索力整体偏差小于10%。

图9 索力调幅及拔出量修正值计算结果
3.3 锚头拔出量修正值
当获取施调索调幅后,实施索力调整存在增量调索法、绝对索力调索法、无应力长度调索法3种方法[24]。绝对索力调索法需严格按照调幅对应的施调顺序进行,难以满足多台张拉设备的并行作业,效率较低;在中等跨径、非线性不强的斜拉桥中,增量调索法可以忽略施调顺序,但施调索密集时邻近索张拉索力相互影响,多台张拉设备不应同时张拉;无应力长度调索法则可规避上述两种方法的不足,完全能达到多步序并行作业的要求,现场仅需对拉张拉端拔出量控制,调索效率明显得到改善。本研究采用无应力长度调索方法,基于公式(1),可推导出计算调幅引起的无应力长度改变量ΔS0,见式(12),其中“1”标识施调前状态,“2”标识施调后状态,E,A,q为已知量,ΔT为施调索调幅计算得到的索力增量。
(12)
l0,l1,T1可由计算索力影响矩阵的有限模型获得。具体步骤:(1)在模拟斜拉索逐根施张阶段之前插入一施工阶段,将一次张拉完毕所测索力作为初始索力赋予对应拉索单元,获取模型中各施调索上下锚点坐标。(2)对设置在模拟斜拉索逐根施张阶段的单位力乘以对应调幅,则非施调索索力增量为0,施调索索力增量对应各自的ΔT,重新执行计算。(3)获取施调索在各自ΔT作用前后锚点3向变形量,代入上下锚点坐标,求解l01,l1,l02,l2,需要注意的是T1并非初次张拉完毕后拉索索力,而是模型中施调索在各自ΔT作用前一阶段所计算的索力。(4)将以上逐元素代入式(12),计算ΔS0。(5)结合拉索锚固构造,核查拔出量改变后拉索是否仍处于有效锚固范围。计算后的锚头拔出量分布及与调幅的对应关系如图10所示。

图10 成桥实测索力分布
3.4 背景桥梁控制效果
二次调索完成后进行桥面铺装施作,索力通测后选取9根相对偏差不满足要求的拉索按照同样方法进行了调整,最终成桥索力分布如图10所示。结果显示相对设计索力偏差全部在10%以内,最大偏差9%,30根索力偏差在5%~9%之间,82根索力相对偏差在5%以内,各拉索张拉端拔出量分布如图11所示。可见70根拉索拔出量为无偏差状态,42根拉索拔出量存在偏离,但均在张拉端锚固构造有效调节范围以内,成桥后结构受力及主梁高程均符合设计要求。
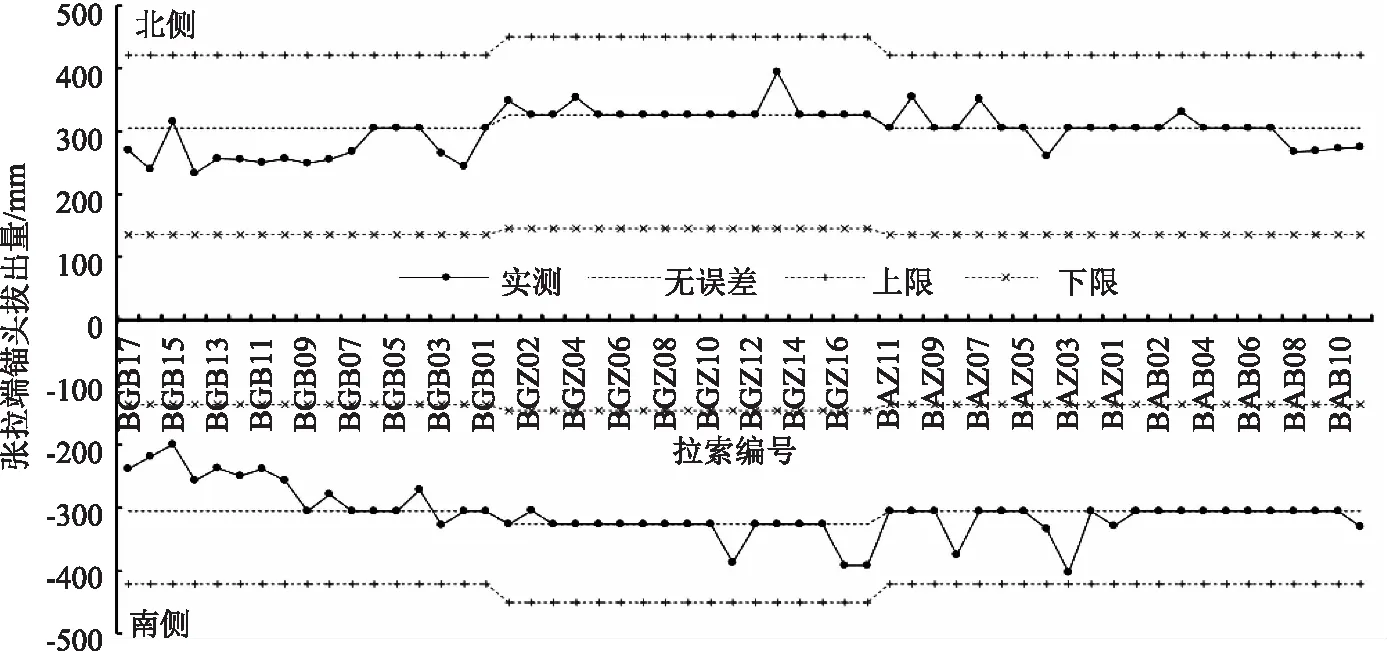
图11 锚头拔出量偏差分布
4 结论
本研究针对某异形钢塔斜拉桥,采用无应力状态控制法对拉索张拉进行控制,并对无应力长度计算、索力标定、二次调索方法进行了研究,主要结论如下:
(1)拉索无应力长度计算应考虑索塔偏位及车道荷载预拱度的影响。
(2)通过实测频率线性标定已知索力的方法,能够满足拉索张拉控制需求,索力识别精度在5%左右,索力识别充分重视线性标定常数项的影响。
(3)基于拉索整体影响矩阵和锁定非施调索调整空间的二次型规划法优化调整模型。一方面避免了针对施调索构建影响矩阵的繁琐;另一方面模型兼顾了施调索对自身之外的其他拉索索力的影响,具有实施简洁、分析全面的优点。
(4)基于改变拉索无应力索长的方式实现了背景桥梁二次调索,大桥成桥索力偏差在5%左右,65%的拉索锚头拔出量处于无偏差状态,其余拉索锚头拔出量均在有效调节范围以内,大桥成桥状态符合要求。
