井洞相连的串珠状缝洞型油藏试井分析方法
2022-11-26程时清李宗泽宋佳忆吴嘉鑫
魏 操,程时清,李宗泽,宋佳忆,汪 洋,吴嘉鑫
(1.中国石油大学(北京)油气田开发与地质国家重点实验室,北京 102249;2.海洋石油工程股份有限公司,天津 300461;3.中航油西南储运有限公司,重庆 401254)
缝洞型油藏一直是油气田勘探开发的热点,近年来,中国在塔里木盆地取得了较好的勘探成果,陆续开发了塔河油田、顺北油田等多个大型缝洞型油藏[1-2]。顺北油田是由大型构造断裂活动和多期岩溶作用形成的断控岩溶油藏,储层埋深超过6 km,地面露头、测井、岩心和地震剖面显示储层发育溶洞、高角度裂缝、溶蚀孔洞和岩石基质4 种介质[3]。溶洞和高角度裂缝的连通关系复杂,水平串珠结构和垂向串珠结构是油藏中最常见的缝洞连通模式[4-5]。钻井过程中,钻杆断裂情况占23%,断裂最长可达29 m;泥浆漏失情况占63.7%,漏失量最大可达3 483.55 m3。这些复杂的地质情况和工程因素给储层评价带来了困难。
试井分析是评价储层的重要手段[6-7],在War⁃ren-Root 模型[8]、Kazemi 模型[9]和De-swaan 模型[10]的基础上,中外学者提出了大量缝洞型油藏试井模型。然而,传统的模型一般考虑三重介质,模型的建立基于经典的达西定律,很难精确描述溶洞中流体流动,特别是当井直接钻入溶洞内[11-15]。随着缝洞型油藏的开发,学者们认识到了溶洞的存在。常学军等考虑裂缝和溶洞与井筒相连,提出了三重介质油藏试井分析方法[16],张福祥等建立了井钻入溶洞内的缝洞型油藏试井模型[17],林加恩等使用管流与渗流耦合来解决溶洞内的渗流问题[18],尹洪军等将溶洞考虑为扩大的井筒,建立了溶洞发育的缝洞型油藏试井解释模型[19],杜鑫等联立质量、能量和动量守恒方程,建立了波动和流动耦合模型来分析井底的压力动态[20-21],在文献[21]的基础上,徐燕东分析了重力对试井特征曲线的影响[22]。但是,上述研究仅考虑了一个溶洞的情况,而串珠状溶洞往往是多个溶洞连接在一起。
围绕串珠状溶洞的试井模型和渗流理论研究,LI 等建立了横向串珠缝洞体产量递减分析模型[23],DU 等利用多区复合模型建立了横向串珠缝洞体试井模型[24]。然而,上述方法只考虑了溶洞、裂缝和基质3种介质,没有考虑溶蚀孔洞;且没有提出针对垂向串珠结构的试井分析方法。
综合分析油藏的地质情况和工程因素,考虑4种介质和重力影响,建立井洞相连的垂向串珠结构试井模型,分析典型特征曲线,将提出的模型在顺北油田进行实例应用和试井解释,提供一种评估串珠状缝洞体储层参数的试井分析方法。
1 模型建立
1.1 物理模型
提出2个溶洞区域和裂缝区域串联的物理模型(图1a)来表征垂向串珠结构(图1b)。井筒直接和溶洞区域相连,溶洞区域仅包含溶洞介质,等效半径为rf,溶洞区域i(i=1,2)的顶高和底高分别为h2(i-1)和h2i-1,由于溶洞区域未充填,流体假设为自由流(即流体穿过溶洞区域的压降很小,建模时可以忽略);裂缝区域包含高角度裂缝、溶蚀孔洞和基质介质,裂缝区域j(j=1,2)的顶高和底高分别为h2j-1和h2j,由于裂缝区域内高角度裂缝比较发育,流动方向考虑为沿垂直方向单向流动,孔洞和基质内流体以拟稳态窜流方式流入裂缝。其他基本假设如下:①储层原始地层压力为pi,单相微可压缩原油的体积系数为B,油井以定产量q生产。②溶洞区域i的储集系数为Cvi,井筒储集系数为C,油藏的综合压缩系数为ct,流体压缩系数为cf。③裂缝区域j中,裂缝、孔洞和基质的渗透率分别为Kfj,Kvj,Kmj,孔隙度分别为ϕfj,ϕvj,ϕmj,流体黏度分别为μfj,μvj,μmj。④考虑重力影响,忽略毛管压力的影响。
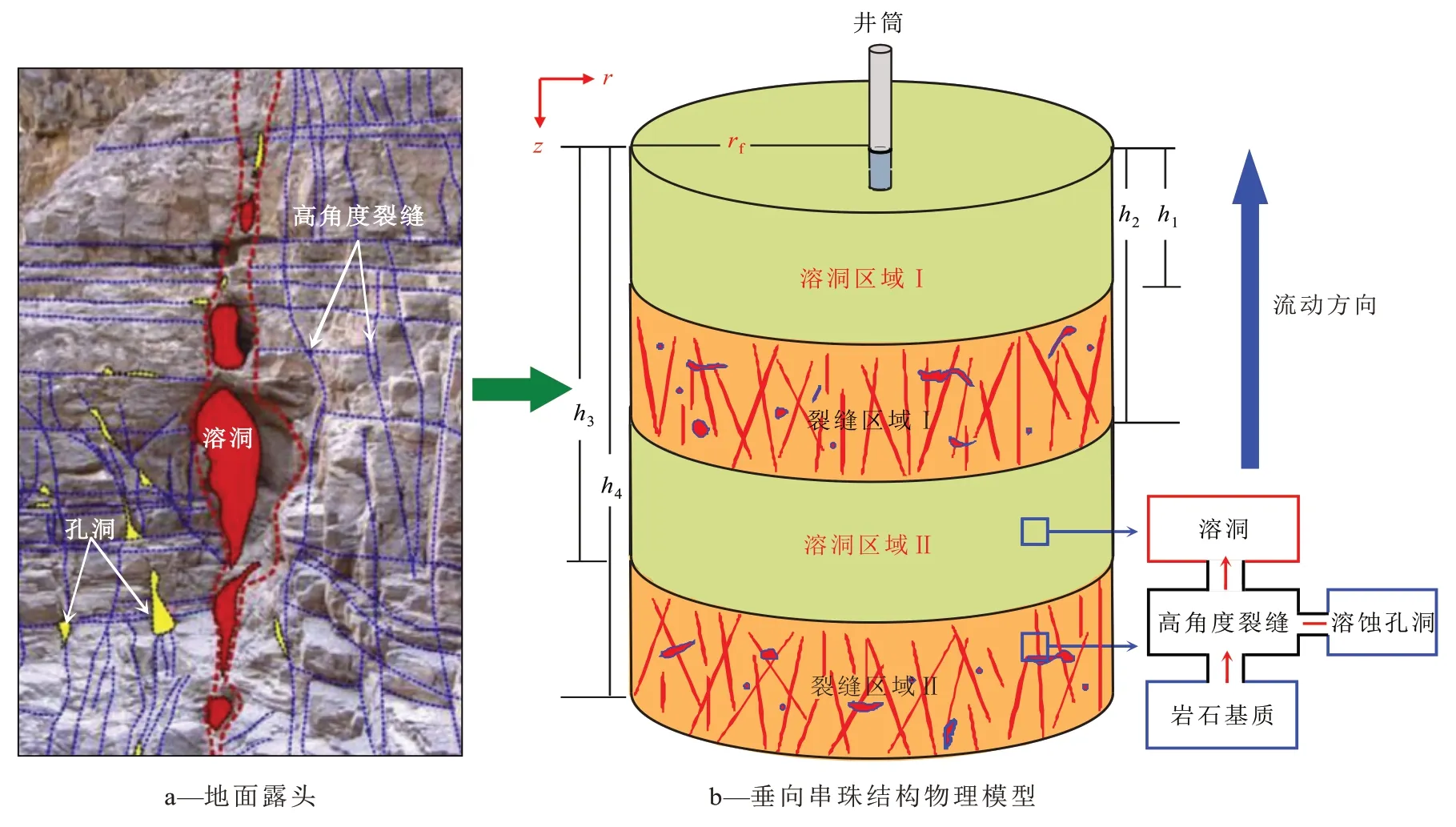
图1 垂向串珠结构示意Fig.1 Vertical beads-on-string structure
1.2 数学模型
1.2.1 模型建立
根据基本假设,溶洞区域内流体遵守自由流,流体流过溶洞区域造成的压降可忽略,易得溶洞区域Ⅰ界面处的压力连续方程为:
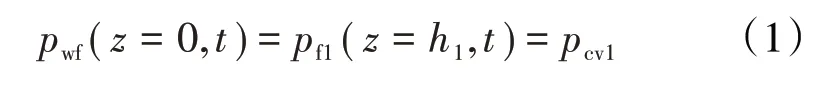
考虑造成溶洞区域Ⅰ内流体质量发生改变的3个因素:①溶洞区域Ⅰ内流体流入井筒。②裂缝区域Ⅰ的流体流入溶洞区域Ⅰ。③岩石和流体的压缩性。根据质量守恒定律,得到溶洞区域Ⅰ的质量连续方程为:
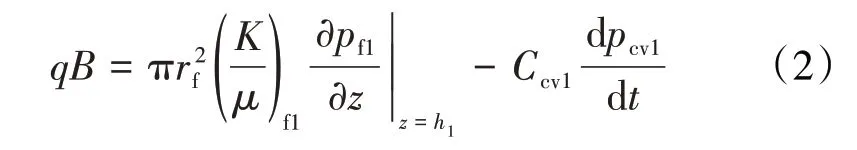
使用相同的方式,溶洞区域Ⅱ界面处的压力连续方程可表示为:
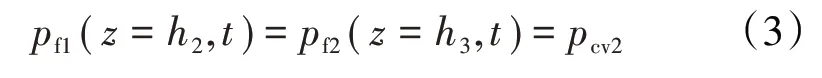
溶洞区域Ⅱ的质量连续方程为:
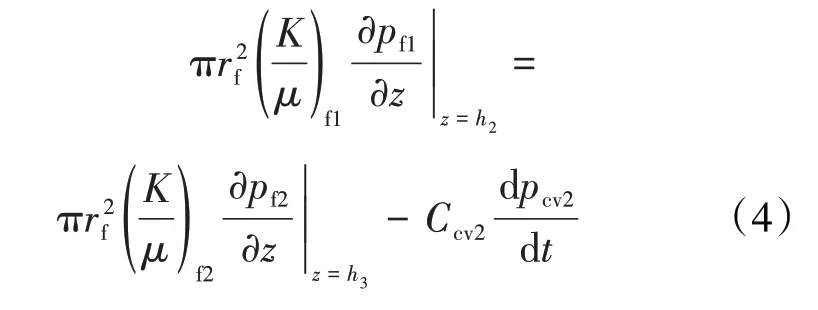
由于裂缝区域Ⅰ的高角度裂缝发育,假设主要的流动为沿着垂直方向的一维线性流动,由于重力方向与流动方向相反,根据达西定律,裂缝区域Ⅰ任意一点的渗流速度为:
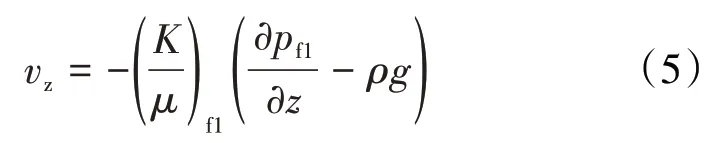
孔洞和基质内流体以拟稳态窜流的方式流入裂缝介质,裂缝区域Ⅰ的质量守恒方程可写为:
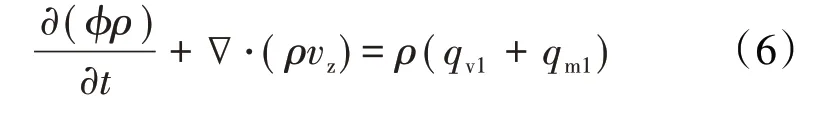
根据Warren-Root 模型,介质之间的窜流量可分别表示为:
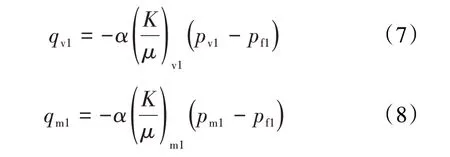
结合岩石和流体的状态方程,将(5),(7)和(8)式分别代入(6)式,得到裂缝区域Ⅰ中裂缝、孔洞、基质的渗流方程分别为:
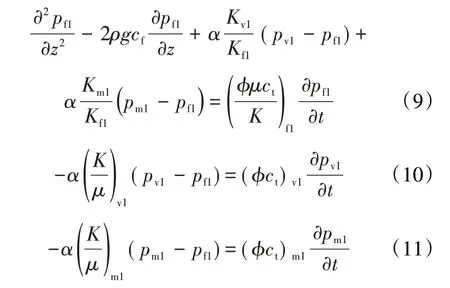
同理可得到裂缝区域Ⅱ中裂缝、孔洞、基质的渗流方程分别为:
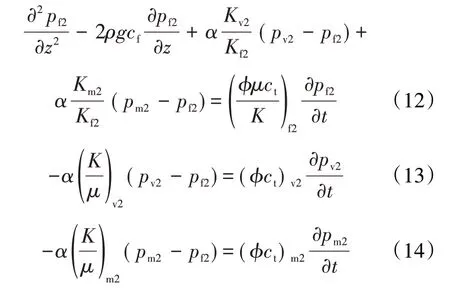
模型的初始条件是:
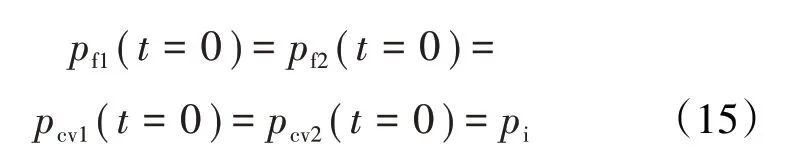
考虑了3种外边界条件:

1.2.2 模型求解
为了便于求解,将(1)—(4)式和(9)—(16)式无量纲化并进行Laplace变换(表1)。

表1 无量纲定义Table1 Dimensionless definitions
得到溶洞区域的无量纲方程组为:
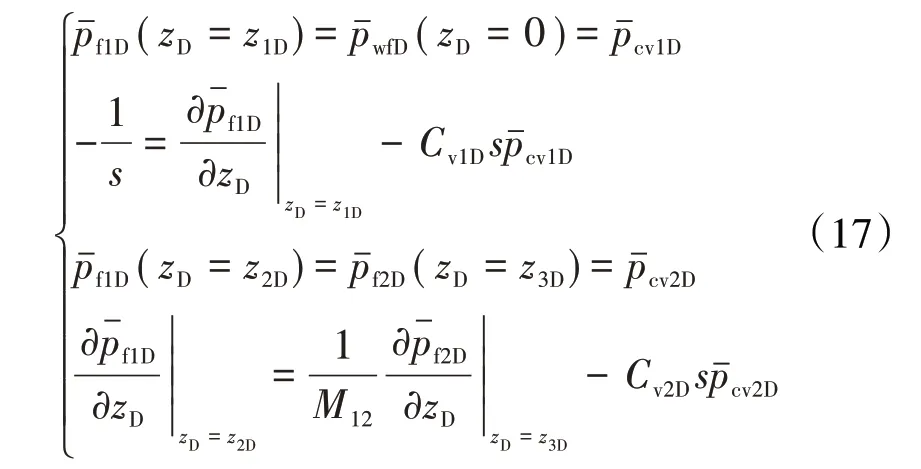
裂缝区域的无量纲方程组为:


根据边界条件和初始条件即可确定c1—c4,获得模型的唯一解。
对于无限大边界:
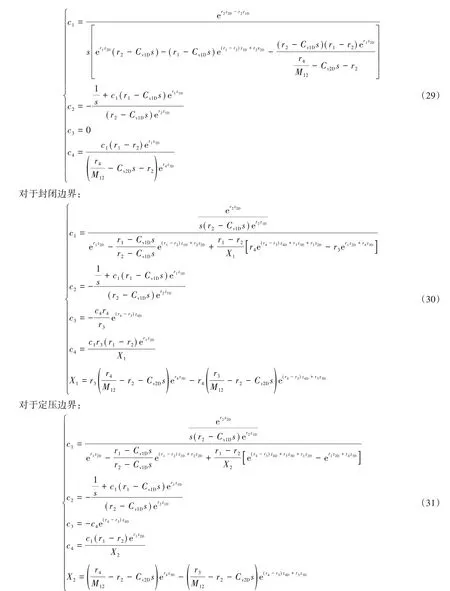
将c1,c2代入(1)式即可得到模型的井底压力解:
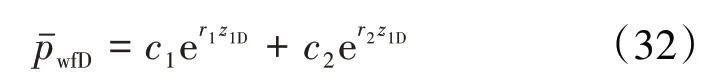
如果考虑井储和表皮效应,利用杜哈美原理获得井底压力解[25]:
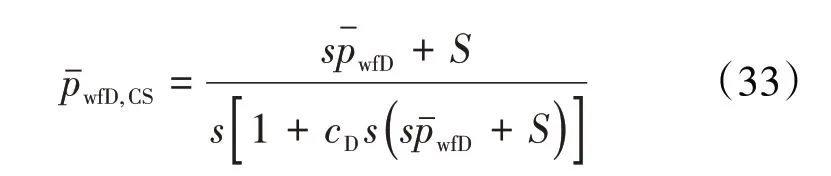
对(33)式进行Stehfest 数值反演即可得到实空间下的井底压力解,绘制双对数图版[26]。
2 典型图版和流动阶段
给定基础参数包括:CD=0.05,S=0.1,Cv1D=10,Cv2D=500,z1D=1,z2D=5,z3D=10,z4D=20,ωf=0.01,ωv=0.14,ωm=0.85,λv=0.001,λm=0.000 1,GD=0,M12=1,W12=1,绘制了垂向串珠结构的试井典型曲线(图2,图3)。由图2和图3可见,试井典型曲线可划分为4个典型流动阶段:①井筒储集阶段,压力与压力导数的斜率为1。②溶洞Ⅰ储集阶段,反映溶洞Ⅰ内的流体流动,典型特征是压力导数曲线“下凹”且出现单位斜率直线。③溶洞Ⅱ储集阶段,反映溶洞Ⅱ内的流体流动,典型特征与溶洞Ⅰ储集阶段的相同。④边界响应段,对于封闭边界,压力和压力导数曲线上翘且斜率为1;对于无限大边界,压力和压力导数曲线的斜率为1/2,反映裂缝区域线性流,这与常规无限大边界的径向流特征有差别;对于定压边界,压力导数曲线下掉。值得注意的是双溶洞模型中裂缝区域的流动特征被溶洞区域掩盖了。为了阐述完整的流动阶段,给出单溶洞单裂缝区域串联的试井典型曲线。裂缝区域主要包含3个流动阶段(图3):①孔洞窜流阶段,压力导数曲线“下凹”。②基质窜流阶段,压力导数曲线“下凹”。③线性流阶段,压力和压力导数曲线的斜率为1/2。与溶洞介质引起的压力导数曲线“下凹”不同,常规多重介质之间窜流引起的压力导数曲线“下凹”的斜率往往不等于1。这为识别溶洞和常规的多重介质提供了理论依据。
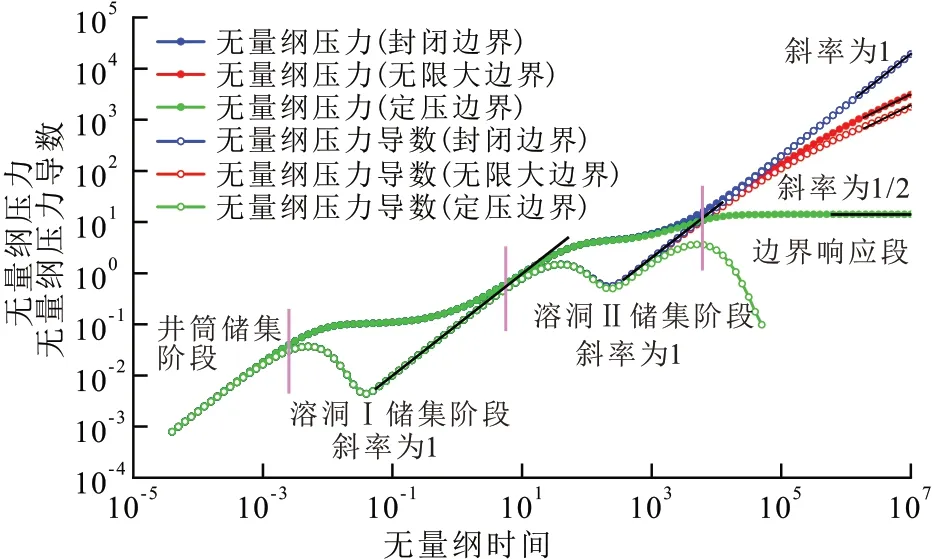
图2 双溶洞双裂缝区域模型试井典型图版Fig.2 Type curves of two-cave-two-region model
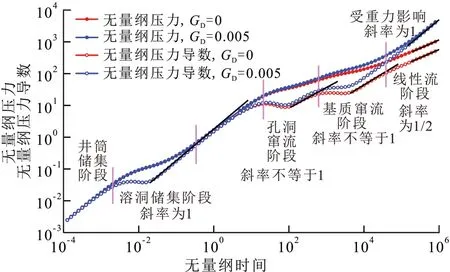
图3 单溶洞单裂缝区域模型试井典型图版Fig.3 Type curves of single-cave-single-region model
另外,分析了重力对试井典型曲线的影响。与封闭边界相似,重力影响下试井典型曲线在后期出现斜率为1的压力和压力导数曲线(图3)。因此,开发串珠状缝洞油藏应考虑重力对流动的影响。顺北油田采取的“注水替油”措施减轻了重力的影响,已经取得了较好的开发效果[27]。
3 参数敏感性
给定基础参数CD=0.05,S=0.1,Cv1D=10,z1D=1,z2D=5,z3D=10,z4D=20,ωf=0.01,ωv=0.14,ωm=0.85,λv=0.001,λm=0.000 1,GD=0,M12=1,W12=1,分析参数敏感性。
3.1 无量纲溶洞储集系数
设置3组不同无量纲溶洞储集系数,即Cv2D分别为300,500,700。由图4可见,无量纲溶洞储集系数主要影响溶洞储集阶段的宽度和深度,无量纲溶洞储集系数越大,下凹的宽度和深度越大。
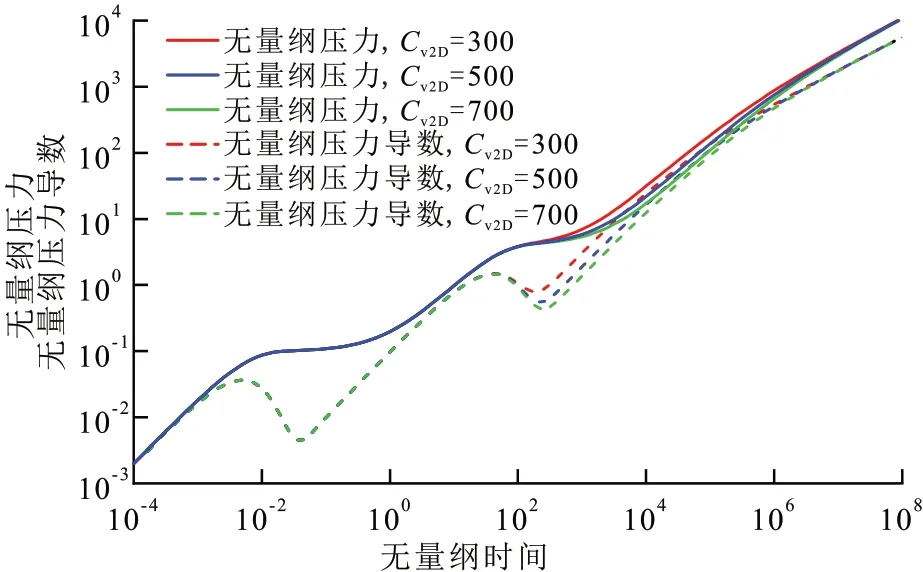
图4 无量纲溶洞储集系数对试井典型曲线的影响Fig.4 Effect of dimensionless cave storage coefficient on type curves
3.2 裂缝长度
保持溶洞Ⅰ的高度不变,改变Z2D来表示不同的裂缝长度,即Z2D分别为3,5,7。由图5可见,裂缝长度主要影响溶洞Ⅱ储集阶段的出现时间,裂缝长度越大,溶洞Ⅱ储集阶段出现时间越晚,因为压力波需要更长的时间穿过裂缝区域。
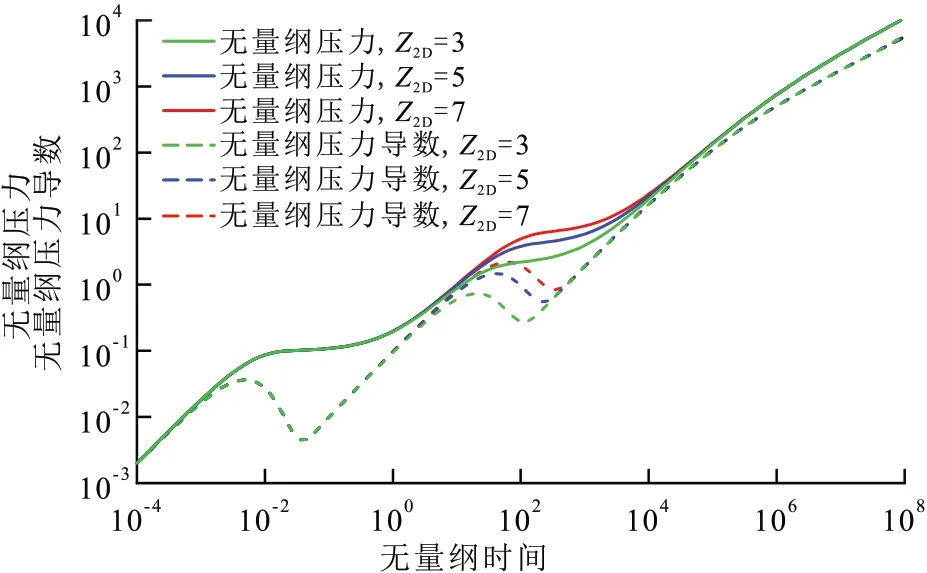
图5 裂缝长度对试井典型曲线的影响Fig.5 Effect of fracture length on type curves
3.3 无量纲重力系数
设置3 组不同无量纲重力系数,即GD分别为0,0.01,0.001。由图6可见,重力影响下试井典型曲线在后期会出现斜率为1 的压力和压力导数曲线,曲线上翘的时间与无量纲重力系数有关,无量纲重力系数越大,曲线上翘的时间越早。因此,重力可以视为封闭边界,重力的大小相当于封闭边界的距离。
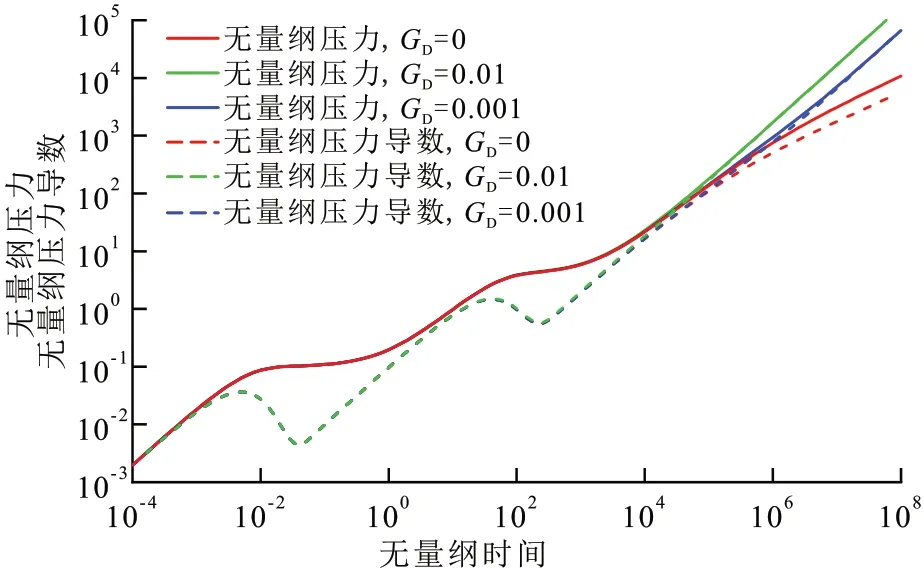
图6 无量纲重力系数对试井典型曲线的影响Fig.6 Effect of dimensionless gravity coefficient on type curves
3.4 窜流系数
设置3 组不同的基质窜流系数,即λm分别为0.000 1,0.000 2,0.000 3,来分析其对试井典型曲线的影响。由图7可见,与常规认识一致,窜流系数主要影响窜流阶段出现的时间,窜流系数越大,窜流阶段出现的时间越早。
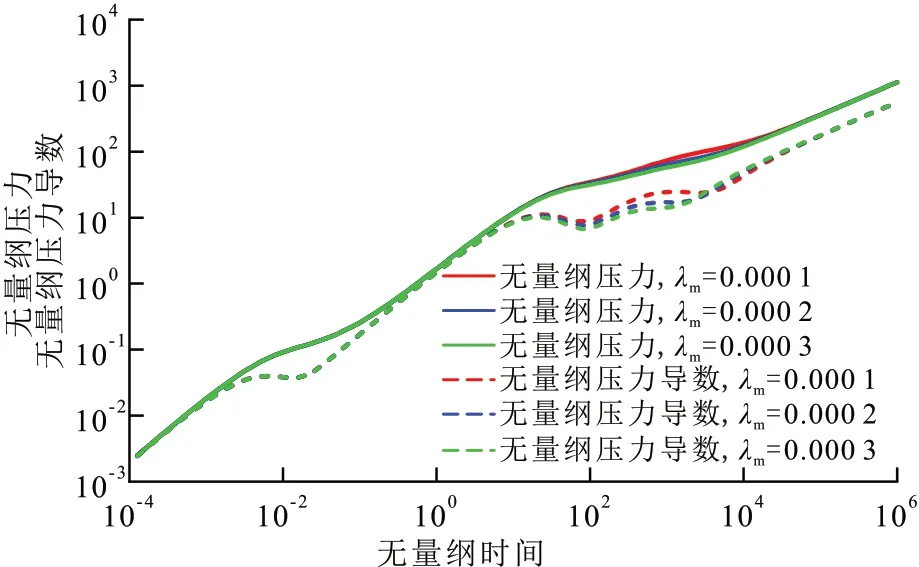
图7 窜流系数对试井典型曲线的影响Fig.7 Effect of interporosity flow coefficient on type curves
3.5 储容比
改变孔洞储容比和基质储容比,即ωv分别为0.10,0.14,0.18,ωm分别为0.81,0.85,0.89,来分析其对试井典型曲线的影响。由图8 可见,储容比主要影响窜流阶段下凹的深度,储容比越大,窜流阶段下凹的深度越大。
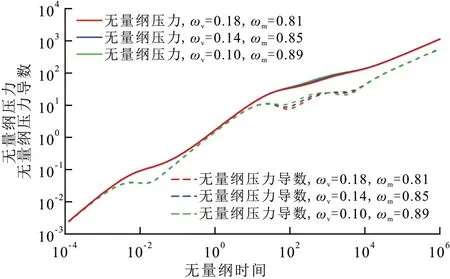
图8 储容比对试井典型曲线的影响Fig.8 Effect of storativity ratio on type curves
4 实例应用
顺北油田是塔里木盆地新发现的断控岩溶油藏,构造破碎带控制着油藏的主要储量,地震剖面显示构造破碎带发育大量的串珠状缝洞体,钻井过程中经常发生钻杆放空和泥浆漏失的情况。现有试井分析方法解释的参数很难与地质情况吻合,为了阐述新建模型的应用,选取顺北油田典型井进行解释。
顺北Y 井钻入垂向串珠状缝洞体(图9),日产量为65 m3/d,压力恢复测试时长为255 h,实测试井曲线出现了溶洞储集阶段和窜流阶段,该井基础参数包括:井径为0.1 m,储层有效孔隙度为10%,综合压缩系数为0.000 836 MPa-1,地层原油体积系数为1.114,地层原油黏度为2.242 mPa·s。使用提出的模型对该井进行解释,理论双对数曲线与实测数据的拟合效果较好(图10),表2列出了试井解释结果,油藏的平均渗透率为796 mD,渗透性较好。此外,还获得了常规试井方法无法解释的溶洞等效半径为52 m,溶洞Ⅰ等效高度为2.6 m。
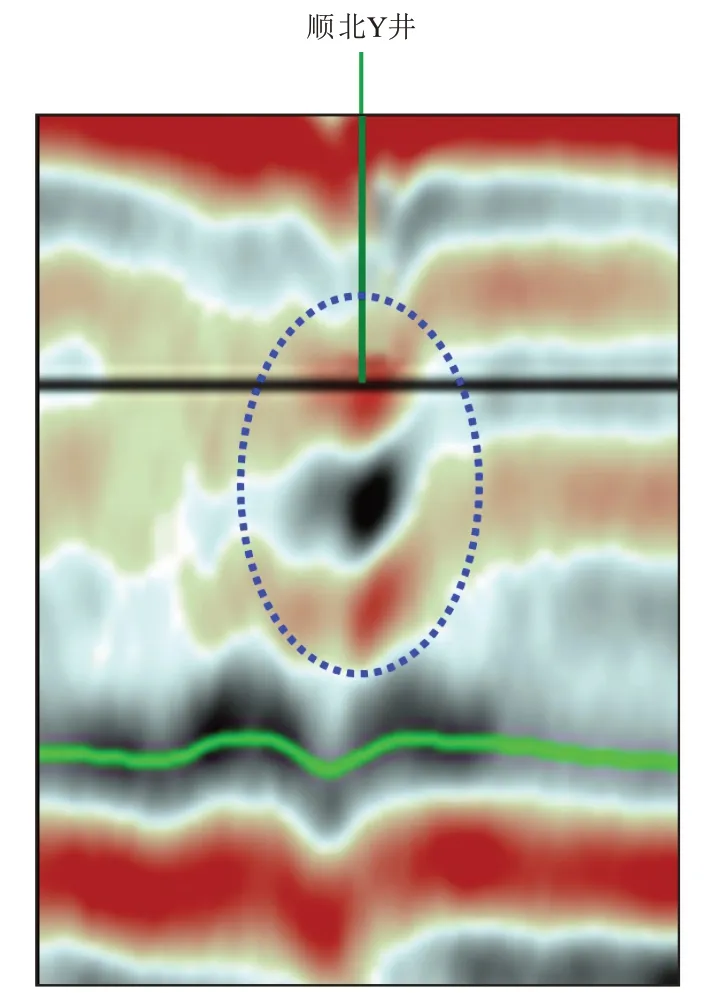
图9 顺北Y井地震剖面Fig.9 Seismic profile of Well Shunbei Y
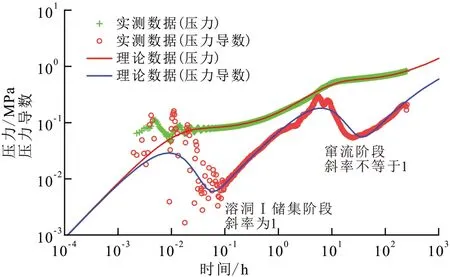
图10 顺北Y井压力和压力导数拟合结果Fig.10 Fitting results of pressure and its derivative of Well Shunbei Y
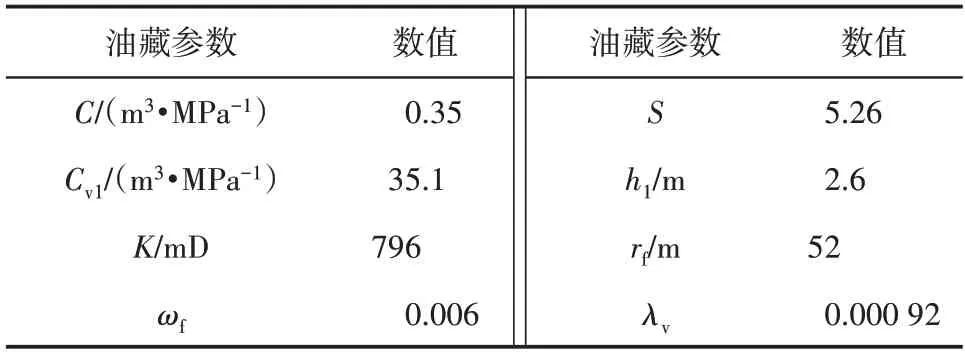
表2 顺北Y井解释结果Table2 Interpretation results of Well Shunbei Y
5 结论
详细分析了3种外边界条件下垂向串珠状缝洞体的试井典型曲线,其典型流动阶段包括溶洞储集阶段和裂缝区域线性流阶段。
溶洞储集阶段和窜流阶段的压力导数曲线都会出现“下凹”,溶洞储集阶段的典型特征是压力导数曲线的斜率为1,而窜流阶段压力导数曲线的斜率不等于1,这为通过试井技术识别溶洞和常规的多重介质提供了理论依据。
在串珠状缝洞体中,重力影响下试井典型曲线会出现类似封闭边界的压力响应特征,开发过程中应采取措施减轻重力的影响以提高串珠状缝洞型油藏的开发效果,顺北油田实施的“注水替油”措施已取得不错的效果。
顺北油田发育垂向串珠状缝洞体,应用新建模型解释了一口典型井,除能解释常规的储层参数外,也能反演现有试井方法无法解释的溶洞等效半径、溶洞等效高度等参数。
符号解释
B——原油体积系数;
c1,c2,c3,c4——常数;
cf——流体压缩系数,Pa-1;
ct——综合压缩系数,Pa-1;
下标cv——溶洞;
C——井筒储集系数,m3/Pa;
Ccv1——溶洞区域Ⅰ储集系数,m3/MPa;
Ccv2——溶洞区域Ⅱ储集系数,m3/MPa;
Cvi——溶洞区域i储集系数,m3/Pa;
下标D——无量纲;
Dj(s)——裂缝区域j窜流函数;
下标f——裂缝介质;
g——重力加速度,m/s2,其值为9.8;
GD——无量纲重力系数;
h——溶洞等效高度,m;
h1——溶洞区域Ⅰ底深,即溶洞Ⅰ等效高度,m;
h2——裂缝区域Ⅰ底深,m;
h3——溶洞区域Ⅱ底深,m;
h4——裂缝区域Ⅱ底深,m;
下标i——溶洞序号,分别为1和2;
下标j——裂缝序号,分别为1和2;
K——渗透率,D;
Kfj,Kmj,Kvj——裂缝区域j的裂缝、基质和孔洞渗透率,D;
Kf,Km,Kv——裂缝、基质和孔洞渗透率,D;
下标m——基质介质;
M1j——裂缝区域Ⅰ和裂缝区域j的流度比;
pcvi——第i个溶洞区域压力,Pa;
pcv1——溶洞区域Ⅰ压力,Pa;
pcv2——溶洞区域Ⅱ压力,Pa;
pf——裂缝压力,Pa;
pfj——裂缝区域j裂缝介质压力,Pa;
pf1——裂缝区域Ⅰ裂缝介质压力,Pa;
pf2——裂缝区域Ⅱ裂缝介质压力,Pa;
pi——原始地层压力,Pa;
pm1——裂缝区域Ⅰ基质介质压力,Pa;
pm2——裂缝区域Ⅱ基质介质压力,Pa;
pv1——裂缝区域Ⅰ孔洞介质压力,Pa;
pv2——裂缝区域Ⅱ孔洞介质压力,Pa;
pwf——井底流压,Pa;
pwf,CS——考虑井储表皮的井底流压,Pa;
q——油井产量,m3/s;
qm1——裂缝区域Ⅰ基质向裂缝的窜流量,m3/s;
qv1——裂缝区域Ⅰ孔洞向裂缝的窜流量,m3/s;
r——径向坐标系;
r1,r2,r3,r4——常数;
rf——溶洞等效半径,m;
rw——井筒半径,m;
s——Laplace变量,无量纲;
S——表皮系数;
t——生产时间,s;
下标v——孔洞介质;
vz——裂缝区域任意一点的渗流速度,m/s;
W1j——裂缝区域Ⅰ和裂缝区域j的储容比;
X1,X2——常数;
z——纵向距离,m;
zD,z1D,z2D,z3D,z4D——无量纲纵向距离;
α——形状因子;
λm,λv——基质、孔洞窜流系数;
λmj,λvj——裂缝区域j的基质、孔洞窜流系数;
μ——流体黏度,Pa·s;
μfj,μmj,μvj——裂缝区域j的裂缝、基质和孔洞流体黏度,Pa·s;
ρ——流体密度,kg/m3;
ϕ——孔隙度;
ϕfj,ϕmj,ϕvj——裂缝区域j的裂缝、基质和孔洞孔隙度;
ωf,ωm,ωv——裂缝、基质和孔洞储容比;
ωfj,ωmj,ωvj——裂缝区域j的裂缝、基质、孔洞储容比。
