废弃橡胶-砂混合物热传导特性与预测模型研究
2022-11-26贾晓敏段隆臣王才进
贾晓敏,张 涛,段隆臣,何 怡,王才进
(1.洛阳理工学院土木工程学院,河南 洛阳 471023;2.中国地质大学(武汉)工程学院,湖北 武汉 430074)
废弃橡胶轮胎是交通运输工程领域产生的一种废弃材料,其产量逐年增加,如何处理大量废弃橡胶轮胎是全世界亟待解决的问题之一[1-2]。将废弃橡胶与砂混合形成橡胶-砂混合物,是一种新型环保轻质复合材料,具有变形能力强、渗透性高和成本低廉等特点,已广泛应用于公路路基[3-4]、垃圾填埋场[5]和各类热工构筑物项目[6]中,具有巨大的工程应用潜力。对于相关热工构筑物的建设应用,废弃橡胶及其混合物的导热性能是工程设计的重要内容之一。
准确获得岩土材料的导热系数是建筑结构温度场分析和能源建筑设计中的关键环节[7-8]。国内外学者对废弃橡胶-砂混合物的导热性能已开展了相关研究。如:Li等[9]对废弃橡胶颗粒改良粉煤灰-黏土的导热性质进行了研究,将废弃橡胶颗粒按质量比0%、1%、2%、3%、5%和7%的比例掺入粉煤灰-黏土中,进行保温试验和导热试验,得出橡胶颗粒改良粉煤灰-黏土具有保温效果良好和导热系数小的结论;Lee等[10]提出采用矿山尾矿与废弃橡胶颗粒混合物作为轻质填充材料,研究了不同混合比的尾矿与废弃橡胶颗粒的热性能和填充性;Lee等[11]研究了含水率、尾矿与废弃橡胶颗粒的配比、压实度和废弃橡胶粒径对废弃橡胶颗粒与尾矿混合物导热性质的影响,认为混合物的导热系数与体积密度呈相关性,水平导热系数略高于垂直导热系数,且对于含水率较低的混合物,其各向异性效应更加明显;Orakoglu等[12]采用瞬态热线法测定玄武岩、玻璃、钢纤维和无筋细颗粒土的导热系数,研究了纤维体积分数、冻融循环和温度对导热系数的影响规律,指出纤维加筋土的导热系数随冻融循环次数和温度的增加而降低;Bandai等[13]研究了饱和多孔介质天然体系热平衡模型中热分散系数与颗粒粒径的关系,认为颗粒粒径的大小会影响基于多孔介质天然体系热平衡模型的热分散系数对流速的依赖性;Yang等[14]通过三维数值模型方法估算废弃橡胶颗粒改性砂浆复合材料的有效导热系数,并采用独立参数估计方法对三维数值模型进行了校正,校正后模型的预测结果与试验实测数据吻合较好;Xiao等[15]研究了颗粒粒径比对废弃橡胶-砂混合物导热系数的影响,认为采用相对粒径较大的废弃橡胶颗粒制得的废弃橡胶-砂混合物的导热系数较高,当橡胶体积掺比为40%时,不同粒径比试样间的导热系数差异可达到20%。综上所述,目前关于系统研究废弃橡胶-砂混合物导热系数的报道相对较少,多因素对废弃橡胶-砂混合物导热系数的综合影响尚不明确,且热量在类似二元混合介质中的热导机理仍需进一步探明。因此,为明确橡胶-砂混合物的传热性能和传热机理,本文选取废弃橡胶颗粒和砂的混合物作为研究对象,通过室内热探针试验测试了不同制备状态下废弃橡胶-砂混合物的导热系数,研究了橡胶掺量、含水率和干密度对废弃橡胶-砂混合物导热系数的影响规律,探讨了废弃橡胶-砂混合物的传热机理;在所得试验数据的基础上,建立了基于人工神经网络技术的导热系数预测模型,并验证了模型计算结果的有效性和适用性。研究成果可为拓展废弃橡胶轮胎的工程应用、研发绿色高效的热工构筑物隔热材料提供借鉴与指导。
1 试验材料与方法
1.1 试验材料与设备
(1) 试验材料。试验用砂选用武汉地区的天然河砂,其颗粒比重Gs为2.61,颗粒粒径在0.40~2.50 mm之间,平均粒径d50为0.57 mm。橡胶颗粒购于废弃轮胎加工厂,由废弃橡胶轮胎经过去除钢丝和杂质,并简单粉碎获得,其颗粒比重Gs为1.22,颗粒粒径在1~3 mm范围,平均粒径d50为2.45 mm。橡胶轮胎中钢丝/钢绞线的存在会加速橡胶的老化速率,同时会增大橡胶“自燃”的风险[16]。试验用天然河砂和橡胶颗粒如图1所示,其颗粒粒径分布曲线见图2。本文橡胶颗粒与砂颗粒的平均粒径d50之比为4.3。

图1 试验用天然河砂和橡胶颗粒

图2 试验用天然河砂和橡胶颗粒的颗粒粒径分布曲线
(2) 试验设备。导热系数测试设备为南京大展机电技术研究所生产的DZDR-S型导热系数测定仪,其测试原理如图3所示。该导热系数测定仪基于瞬态平面热源技术(TPS),能够广泛地测试固体、液体和粉末的热传导性能。TPS技术是基于无限大介质中阶跃加热的圆盘形热源产生的瞬态温度相应,圆盘形的平面探头可同时作为热源和温度传感器,通过相应的热量损失来计算测试样品的导热系数,是一种较为精确、快速、便捷的测试手段。本文所用TPS探针的直径为15 mm,测试精度为±3%。

图3 热探针测试装置示意图
1.2 试验方法
首先,将橡胶颗粒均匀分散,若其中含有较多水分,则需将其风干后再使用;然后,将干燥的橡胶颗粒与干燥的砂颗粒混合均匀,混合采用电动搅拌器,转速为120 r/min,搅拌时间为5 min;最后,根据设计的目标含水率,将相应质量的水加入搅拌均匀的混合物中,再次搅拌5 min,获得混合均匀、湿润的橡胶-砂混合物,将该混合物密封于塑料袋中,并在室内环境(20℃±2℃,相对湿度40%±5%)中静置12 h以上,以确保水分充分浸润橡胶颗粒和砂颗粒。
本文将废弃橡胶-砂混合物中橡胶颗粒掺量设置为0%、5%、10%、15%、20%、25%、30%、35%、40%、50%和100%,橡胶掺量为橡胶颗粒质量占干混合物总质量的百分比,即:
(1)
式中:Rc为橡胶掺量(%);mr为风干橡胶颗粒质量(g);ms为烘干砂质量(g)。
为研究含水率和干密度对废弃橡胶-砂混合物导热系数的影响规律,本文配置了含水率0%、2%、6%、8%和10%以及干密度在0.8~1.4 g/cm3范围的试样,进行导热系数测试(最大含水率设置为10%,因为当含水率超过10%时,在拌合、静置和测试过程中会出现“沥水”等不良现象,影响测试结果的精确性)。将混合均匀的不同含水率和橡胶掺量的废弃橡胶-砂混合物试样,按照计算的干密度分层填筑于边长为10 cm的立方体透明模具中,可有效避免“尺寸效应”产生的测试误差。
2 试验结果与分析
多孔岩土材料的导热系数主要受两个方面因素的影响,即自身材料化学成分/矿物成分和外部贮存状态。本文选用的橡胶颗粒材料来源于相同的汽车轮胎品牌,其橡胶类型和化学成分含量基本相同;砂来源于同一采样场地,其矿物成分也大致相同。因此,橡胶-砂混合物试样的导热系数主要与制备时的橡胶颗粒含量、含水率和干密度密切相关。
2.1 橡胶掺量对橡胶-砂混合物导热系数的影响
在干密度为1.0 g/cm3情况下,不同含水率橡胶-砂混合物试样的导热系数随橡胶掺量的变化曲线,见图4。

图4 不同含水率橡胶-砂混合物试样的导热系数随橡胶掺量的变化曲线
由图4可知:随着橡胶掺量的增加,橡胶-砂混合物的导热系数整体呈降低趋势,当橡胶掺量增至100%时(纯橡胶试样),不同含水率橡胶-砂混合物试样的导热系数值降至最低,且相互之间差异不大,不同含水率橡胶-砂混合物试样导热系数的降低幅度随含水率的不同而不同,含水率越高,导热系数的降幅越显著。
通过对试验用河砂进行矿物成分分析得到,其SiO2的含量为64.4%,主要矿物成分为石英。众所周知,石英的导热系数约为7.69 W/(m·K)[17],而橡胶的导热系数约为0.25 W/(m·K)[18],前者约为后者的30倍。这表明,砂的导热能力远大于橡胶颗粒,低导热系数橡胶的掺入会阻碍热量在橡胶-砂混合物中的传递,导致橡胶-砂混合物的导热系数随橡胶掺量的增加而降低。当混合物试样为纯橡胶颗粒时,热量在介质中的传递途径主要为橡胶颗粒和孔隙水,且两者导热系数值相差不大(纯水的导热系数约为0.60 W/(m·K),20℃)[19],因此试样的导热系数值降至最低且相互之间差异不显著。值得注意的是,当橡胶掺量较低时,橡胶-砂混合物试样中的传热路径主要为砂-砂接触和孔隙水;随着橡胶掺量的增加,砂颗粒逐渐被橡胶颗粒替代,其传热路径相应地转变为橡胶-橡胶接触和孔隙水,这也是造成混合物试样导热系数不断降低的原因。此外,从图4还可以看出,橡胶-砂混合物的导热系数随橡胶掺量增加存在少量不均与起伏,这主要是因为TPS探针与橡胶-砂混合物存在局部不均匀接触,因而影响了测试结果的精度。
2.2 含水率对橡胶-砂混合物导热系数的影响
在干密度为1.0 g/cm3情况下,纯砂和纯橡胶试样的导热系数随含水率的变化曲线,见图5。

图5 纯砂和纯橡胶试样的导热系数随含水率的变化曲线
由图5可知:对于纯砂而言,其导热系数随含水率的增加而明显增加,当含水率在0~6%范围时,砂导热系数的增幅明显,随后增幅逐渐降低,在干密度1.0 g/cm3的情况下,干砂(含水率等于0%)的导热系数为0.369 W/(m·K),含水率增加至10%时,相应的导热系数值为0.954 W/(m·K),这一试验结果与张涛等[20]对南京四类土体(黏土、粉土、细砂和粗砂)热传导特征的研究结果一致,即干燥的砂土中添加少量水分后,土体的热阻系数(导热系数的倒数)会有显著降低,随着土体含水率接近饱和,其热阻系数趋于定值;对于纯橡胶试样而言,含水率对其导热系数的影响不明显,纯橡胶试样的导热系数随含水率的增加略有增大,当含水率从0%增加至10%时,纯橡胶导热系数从0.263 W/(m·K)增加至0.366 W/(m·K),导热系数增量约为0.1 W/(m·K),造成这种现象的主要原因是橡胶颗粒自身的低热导性,水分的添加并未实质改善橡胶颗粒的传热路径和传热效率。
不同干密度情况下不同橡胶掺量的橡胶-砂混合物试样导热系数随含水率的变化曲线,见图6。
由图6可知:橡胶-砂混合物试样的导热系数随含水率的变化与图5中纯砂和纯橡胶试样的变化均不相同。整体而言,随着含水率的增加,橡胶-砂混合物试样的导热系数均有不同程度的增大,但增幅的大小与橡胶掺量密切相关:当橡胶掺量较低时(5%橡胶掺量),不同干密度情况下橡胶-砂混合物试样的导热系数随含水率的变化与纯砂类似,含水率从0%增加至6%时,导热系数明显快速增大,含水率继续增加后,导热系数的增加趋于稳定[见图6(a)];当橡胶掺量中等时(10%~20%橡胶掺量),不同干密度情况下橡胶-砂混合物试样的导热系数随含水率增加的增幅略有降低[见图6(b)和(c)];当橡胶掺量较高时(40%橡胶掺量),不同干密度情况下橡胶-砂混合物试样的导热系数略有增加但增幅明显小于低橡胶掺量试样[见图6(d)]。橡胶-砂混合物试样的导热系数随含水率的变化特征介于纯砂和纯橡胶试样之间,低导热性能橡胶颗粒的添加会削弱含水率对橡胶-砂混合物导热系数的影响。

图6 不同干密度情况下不同橡胶掺量的橡胶-砂混合物试样导热系数随含水率的变化曲线
已有学者在研究含水率对岩土材料导热系数的影响时,提出了“临界含水率”的概念[19],如图7所示。对于多孔颗粒材料而言,不论细粒土(如黏性土)与粗粒土(如砂性土),其导热系数随含水率的增加而增大均会大致经历不稳定区域和稳定区域两个阶段,导热系数趋于最大值时对应的含水率为“临界含水率”[21]。本文将“临界含水率”的概念应用于橡胶-砂混合物中,可以得到本文橡胶-砂混合物的临界含水率约为8%,超过临界含水率后,多余水分的添加对于提升橡胶-砂混合物导热系数的作用并不明显。这一结论对橡胶-砂混合物在隔热材料中的应用设计具有重要意义。需要指出的是,“临界含水率”来源于砂土类多孔材料,对于橡胶-砂类二元颗粒介质的适用性和有效性仍需更多的试验来进行验证。

图7 典型土体导热系数与含水率的相互关系
2.3 干密度对橡胶-砂混合物导热系数的影响
干密度是表征试样密实程度的参数之一,与颗粒间的接触状态密切相关。一般而言,橡胶-砂混合物的干密度越大,试样越密实,颗粒之间的接触状态越好;反之,则试样松散,颗粒间接触相对较差。热量在混合物中传递的效率与颗粒之间的接触状态紧密相关。
不同含水率情况下不同橡胶掺量的橡胶-砂混合物试样导热系数随干密度的变化曲线,见图8。

图8 不同含水率情况下不同橡胶掺量的橡胶-砂混合物试样导热系数随干密度的变化曲线
由图8可以看出,整体而言,随着干密度的增加,橡胶-砂混合物试样的导热系数呈增长趋势。对于低橡胶掺量的橡胶-砂混合物试样,其导热系数随干密度的增加增幅明显;当橡胶掺量不断增加时,改善橡胶-砂混合物试样的密实度对于提高其导热系数的效果不显著。例如:橡胶掺量为5%、含水率为10%的橡胶-砂混合物试样,干密度从1.0 g/cm3增加至1.3 g/cm3,相应的导热系数从0.639 W/(m·K)增至1.130 W/(m·K),其导热系数的增幅为0.491 W/(m·K);而橡胶掺量为40%、含水率为10%的橡胶-砂混合物试样,干密度从0.7 g/cm3增加至1.0 g/cm3,其导热系数的增幅只有0.118 W/(m·K)。相同橡胶掺量、不同含水率的橡胶-砂混合物试样的导热系数随干密度的变化规律不同,含水率低的橡胶-砂混合物试样,其导热系数随干密度变化的灵敏度较低;而含水率高的橡胶-砂混合物试样,其导热系数随干密度变化的灵敏度相对较高。
综上所述,干密度对橡胶-砂混合物试样导热系数的影响不是单一的,其受到橡胶掺量和含水率等其他因素联合作用的影响。在评价橡胶-砂混合物的导热性能时,应综合考虑这些因素的影响以及这些影响因素之间的相关关系。
3 橡胶-砂混合物导热系数预测模型的建立
根据前述室内热探针试验结果可知,橡胶-砂混合物的导热系数受多个因素的影响,如颗粒材料的化学成分/矿物成分、含水率、干密度、颗粒粒径和接触状态等,采用传统经验关系式难以获得较为满意的预测精度。为此,本文借助于神经网络技术,尝试建立用于评价橡胶-砂混合物导热系数的计算模型,并验证模型的有效性和适用性。
3.1 人工神经网络
人工神经网络是由高度互联的神经元组成的复杂网络,是基于模仿人类大脑结构和功能而构成的信息处理系统,其主要应用于优化、分类和预测。典型的神经网络由输入层(P1、P2、P3)、一个或多个隐藏层(H1、H2)和输出层(R1)组成,每层之间通过神经元联系[见图9(a)]。隐藏层的数量取决于模式识别问题的复杂程度,一个或两个隐藏层对于大多数岩土工程问题是非常有效的[22]。目前反向传播算法是最常用的神经网络算法,在岩土工程领域有着广泛的应用[23]。该算法通过隐藏层的神经元权重相乘,对乘积进行求和,然后使用非线性传递函数来得到输出层R1。本文借助商业软件MATLAB完成人工神经计算模型的构建和实现,模型计算流程图详见文献[22],为避免重复,此处不再赘述。模型训练阶段采用Levenberg-Marquardt反向传播算法,非线性传递函数为sigmoid函数,并将数据划分为训练集、验证集和测试集用于交叉验证,分别占整个数据库总量的55%、25%和20%。通过反向传播原理,神经网络在迭代计算后,通过更新神经元的权重和阈值来不断“学习”,直至训练对象的均方误差最小,且在指定的误差范围内时停止训练[如图9(b)所示]。反馈神经网络模型的性能可以借助相关误差标准参数来评估,常见的有相关系数R2、均方根误差RMSE和方差比VAF等。一个训练有素的神经网络模型应该是R2的值接近1并且误差项的值很小。

图9 人工神经网络计算结构模型
3.2 预测模型的建立
选择橡胶掺量Rc、含水率w和干密度ρd作为橡胶-砂混合物导热系数预测模型的3个输入参数,输出参数为导热系数λ,所有参数均需进行归一化处理,使其值在0~1范围内,归一化计算式为
(1)
式中:xN为归一化后数值;x为参数实际值;xmin为参数实际最小值;xmax为参数实际最大值。
一般地,将试验获得的数据集分成训练集和验证集两个子集,其中训练集用于构建神经网络模型,验证集用于评价网络模型的性能。然而,两个子集的做法可能会导致过度拟合,导致建立的训练模型无法推广至新的数据集。因此,交叉验证方法常用于解决这一问题,其将数据集划分为训练、验证和测试3个子集。当验证集误差开始增加时,由于它被认为是泛化的最佳点,则停止训练。本文将数据库总量的55%、25%和20%数据分别用于训练、验证和测试。
橡胶-砂混合物试样导热系数神经网络预测模型均方根误差随训练次数的变化,即神经网络预测模型训练性能如图10所示。

图10 神经网络预测模型训练性能
由图10可知:随着训练次数的增加,均方根误差逐渐减小,当预测模型达到最佳性能时,均方根误差值为一定值;本文建立的预测模型在训练38次时达到最佳性能,验证集的导热系数均方根误差为0.002 88 W/(m·K)。
3.3 预测模型性能评价
训练、验证和测试3个数据子集的计算结果性能指标,见表1。
由表1可知:3个数据子集的训练结果良好,相关系数R2均高于0.85,方差比VAF均大于85%,均方根误差RMSE值均在0.05 W/(m·K)左右,表明所构建的人工神经网络预测模型在经过有限的训练次数后,能够很好地描述实测的橡胶-砂导热系数值,模型性能优良。

表1 3个数据子集模型计算结果性能指标
为进一步验证所建预测模型的有效性,将整个数据集应用于训练完成的神经网络预测模型,对橡胶-砂混合物试样导热系数预测值和实测值进行对比,结果见图11。
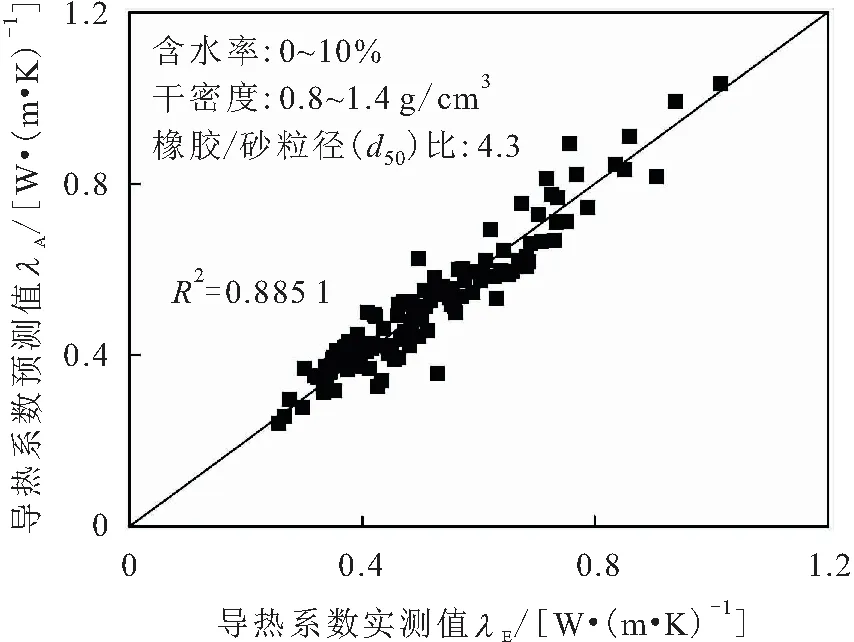
图11 橡胶-砂混合物试样导热系数模型预测值与实测值的对比
由图11可知,导热系数模型预测值λA与实测值λE吻合较好,两者之间的相关系数R2为0.885 1,相对误差绝对值小于10%。这表明,人工神经网络预测模型可以较好地预测橡胶-砂混合物的导热系数,计算精度满足工程设计的需求,同时克服了传统经验关系模型难以适应新的计算对象的局限。
4 结 论
(1) 添加橡胶颗粒会显著降低砂的导热性能,橡胶-砂混合物的导热系数随橡胶掺量的增加而逐渐降低,导热系数的降幅与含水率密切相关。含水率越高,导热系数的降幅越大,但随着橡胶掺量的持续增加,不同含水率橡胶-砂混合物的导热系数相差不大。
(2) 含水率对橡胶-砂混合物导热系数的影响规律不同于纯砂和纯橡胶颗粒,增加混合物的含水率会增加其导热系数,含水率超过“临界含水率”后,导热系数表现为最大且基本不变,本文橡胶-砂混合物的临界含水率约为8%。
(3) 干密度越大,砂、橡胶颗粒之间的接触越紧密,有利于提高热量在橡胶-砂混合物中的传输效率,表现为导热系数的增大。橡胶掺量、含水率、干密度等因素对橡胶-砂混合物导热系数的影响是相互联系的,综合作用于混合物的导热性能。
(4) 选择橡胶掺量、含水率和干密度3个输入参数的人工神经网络预测模型,可较好地估算橡胶-砂混合物的导热系数,计算模型在经历数十次的训练后达到性能最佳,预测值与实测值的相关系数R2大于0.85,相对误差绝对值小于10%,可满足工程设计的需求。橡胶、砂颗粒的大小和形貌亦会对其混合物的导热性能产生影响,今后可对此方面开展进一步研究,以深刻揭示橡胶-砂混合物的传热机理。
