基于新型趋近律的全局快速Terminal滑模PMLSM控制*

索宇超,张 博,杨永宝,艾雄雄,邓 斌,王 杰

(西安工程大学 电子信息学院，陕西 西安 710600)

0 引 言

永磁直线同步电机(PMLSM)可直接将电能转换成直线运动，其具有结构简单、响应速度快等优点，因此广泛应用于智能机器人、计算机数控、XY平台等自动化设备中[1-3]。然而，PMLSM是一个多变量、非线性、不可确定的对象[4-5]。由于采用直接驱动方式，减少了中间缓冲机构，使很多不确定的因素作用于PMLSM上，如控制系统的参数变化和负载扰动。因此，改善PMLSM动态轨迹跟踪及补偿是十分重要的。

滑模控制(SMC)在电机控制领域有着广泛的应用，具有极大的优越性。当系统到达滑模面时，通过滑模切换法保证系统状态变量达到平衡点位置，系统状态不易受参数变化和负载扰动等不利因素的影响[6]。但较大的控制增益会带来严重的抖振现象，并且存在响应速度慢的问题[7]。为了减少抖振，提高系统响应速度，国内外学者提出了不同的滑模趋近律控制算法抑制系统抖振现象。文献[8]设计了变指数趋近律方法，通过幂次项和指数项可以加快到达滑模面，但当负载扰动过大时，系统的精度会变差。文献[9]提出了模糊指数趋近律，基于模糊规则，重新定义切换功能，减弱系统抖振，但该种方法仅存在于理论研究中。文献[10]中提出的一种新型SMC采取了边带宽趋近的方式，并通过引进反双曲正弦函数等特征，比较有效地抑制了系统抖振。但系统受到较大参数变化时，系统响应速度变慢，跟踪精度变差。

综上所述，本文提出了一种基于新型趋近律的全局快速终端SMC方法。该算法采用新型全局快速终端滑动模态，并在结合传统的幂次滑模趋近律的基础上引入Fal函数设计的控制器进行位置跟踪，以减少系统的稳态误差，提高系统响应速度，改善系统抖振现象。同时采用所设计的干扰观测器估计PMLSM控制系统的负载扰动，实现系统的前馈补偿，并对观测的误差进行补偿，以增强鲁棒性，提高系统的动态性能。最后通过仿真分析验证本文所提控制方法的扰动补偿能力、位置跟踪误差和系统的鲁棒性。

1 PMLSM数学模型

PMLSM伺服系统[11-13]大多数是一种非线性、不可确定的系统，为了降低其控制难度，对PMLSM伺服系统进行矢量定向控制，即采用d轴电流id=0的磁场定向控制，电磁推力方程简化为

Fe=kfiq

(1)

PMLSM运动方程为

(2)

式中:M为动子质量；v为动子速度；B为黏滞摩擦系数；Fs为负载扰动及系统摩擦力等不确定的因素总和。

为了简化系统分析，忽略系统摩擦，PMLSM系统的运动方程为

(3)

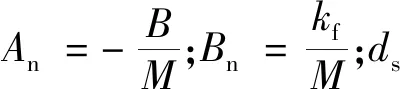
定义状态变量：

(4)

由式(3)、式(4)得到状态方程为

(5)

式中:u为系统的控制输入,u=iq；y为系统输出位置信号；x0为给定的位置参考信号。

2 控制器设计

2.1 滑动模态函数设计

基于新型趋近律的全局快速终端SMC PMLSM伺服系统的控制策略框图如图1所示。定义PMLSM位置与速度误差分别为

e=x1-xs

(6)

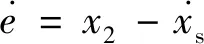
(7)

式中：x1为电机实际位置信号;xs为能够跟踪任意给定输出的位置信号。

针对结构复杂线性SMC的系统趋近律设计,需要构建适合的线性滑模切换面，在此基础上设计SMC函数，改善控制器系统运行轨迹促使其以更加快速平滑的方式沿着滑模面运动。传统的快速终端SMC方法中，假设整个系统状态均处于逐步接近或近似平衡状态时，与非线性快速滑动模态的收敛速度相比，线性滑动模态的收敛速度明显更快。

图1 基于新型趋近律的全局快速终端PMLSM伺服系统控制策略框图

综合考虑线性滑动模态与快速终端滑动模态，定义新型全局快速终端滑模面：

(8)

式中:k1和k2>0；α和β为正奇数且β>α。

系统状态到达滑模面时(s=0)，有：

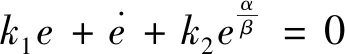
(9)

由式(9)得：

(10)

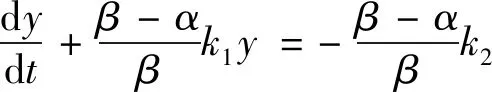
(11)

式(11)解为

(12)

当t=0时，C=y(0)，式(12)变为

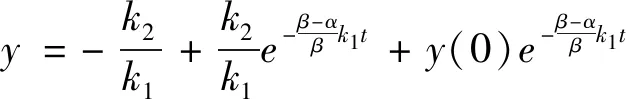
(13)

系统的收敛时间为t,式(13)变为

(14)

由于k1和k2>0,α和β为正奇数且β>α,y(0)=e(0)(β-α/β),则在滑动模态基础上，任意从初始状态e(0)≠0收敛到平衡滑动状态e=0的收敛时间为

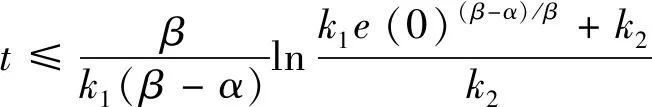
(15)

式(15)在确定了滑模面和其参数时，系统的跟踪误差就可以保证在有限时间周期内沿滑模面收敛为0。

2.2 新型滑模趋近律控制设计

趋近律能使系统从初始状态收敛到滑模面，并保证系统状态在滑模面上，选取合适的趋近律可以在相同抖振下，更快地趋近于0，减少系统抖振[14-15]。

为了更合理地设计SMC从而采用幂次趋近律。幂次趋近律表达式定义为

(16)

式中：k>0;0<∂<1。

当系统状态在远离滑模面时，通过调整∂值可以保证整个系统的运动状态能以一种相对较大的速度趋近于滑模面;当系统状态趋近滑动模态时，调整∂值促使系统具有较小幅度变化的控制增益，从而降低抖振。

由以上分析可知，幂次趋近律虽然可以在一定程度上增加趋近速度，但接近滑模面时，系统抖振严重，滑模增益为0时，影响系统的鲁棒性。

为了提高PMLSM伺服系统的动态品质，进一步削弱系统抖振。本文在幂次趋近律的基础上进行改进，改进后的新型趋近律表达式为

(17)

利用Fal函数进行平滑处理，Fal函数的表达式为

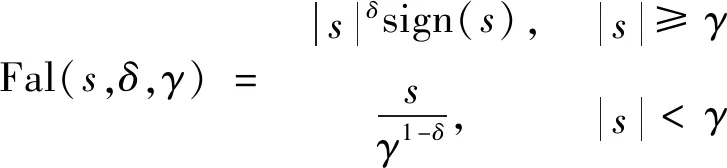
(18)

式中：ε>0;0<δ<1;0<γ<1。

使用Fal函数代替开关函数促使系统运动过程在滑模面上趋近原点时更加简单和平滑，依据s函数值的变化情况对系统趋近速率实时动态地调整，降低系统抖振。Fal(s)、双曲正切函数、sat(s)以及sign(s)运动轨迹示意图如图2所示。

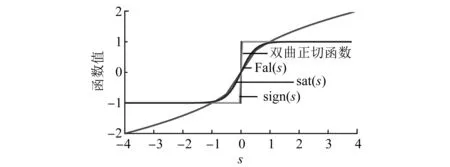
图2 Fal(s)、双曲正切函数、sat(s)和sign(s)的运动轨迹示意图

对式(8)两边同时求导，并将式(5)、式(6)、式(7)和式(17)全部代入，得到控制率u为

(19)

为了提高PMLSM控制精度，在SMC外采用干扰观测器对系统扰动等进行前馈补偿，估计外部扰动ds，提高系统的抗干扰能力。

2.3 干扰观测器设计

观测器是用估计输出与实际输出的差值对估计值进行修正，因此可以将干扰观测器设计为[16]

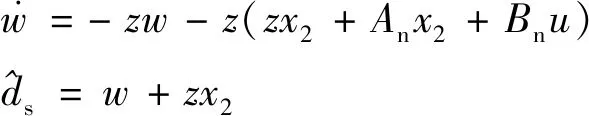
(20)

(21)

对式(21)进行微分方程求解得：

(22)

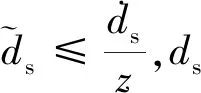
3 系统稳定性分析

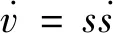
(23)

将式(17)代入式(23)得：

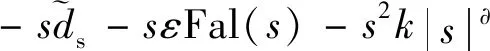
(24)

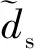
根据以上理论分析，基于新型趋近控制器的式(19)可以写为

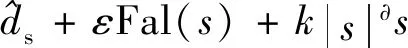
(25)

4 仿真分析

基于以上理论，设计出了基于新型趋近律的全局快速终端SMC。为了证明本文所提新型趋近律的全速快速终端SMC策略的有效性与准确性，对PMLSM驱动位置控制系统设计进行仿真分析，PMLSM的各项参数如表1所示。

表1 电机参数

控制器的各项参数为k1=40,k2=30,α=1.8,β=1.5,k=14.8,ε=0.5,δ=0.5,γ=0.5,∂=0.8。

为了验证本文所提出的控制策略，与传统的幂次趋近律进行比较，传统幂次趋近律如下：

u=iq=

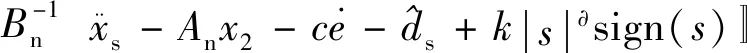
(26)

4.1 输入位置信号为正弦波信号

为了验证所设计控制器的跟踪性能，位置信号设定为1.5 mm、频率为1.5 Hz。在4 s时施加外部扰动，其值为40 N，基于传统的幂次趋近律和本文提出的控制方法，位置跟踪误差曲线如图3所示。图4和图5分别为基于传统幂次趋近律与本文所提出控制方法的位置误差曲线。由图4可知，传统幂次趋近律控制方法的位置误差在电机刚运行时上升到0.28 mm，并且出现了跳跃，在0.5 s时误差逐渐接近0。在4 s时，突加外部扰动40 N，位置误差突然增加到5 mm，在4.12 s左右稳定，但稳定在0.2 mm附近，并伴随抖振。由图5可知，本文提出控制方法的位置误差在电机刚运行时，位置误差在0.12 mm，在0.2 s时误差逐渐趋于稳定。在4 s时，突加外部扰动40 N，位置误差增加到2 mm，在4.09 s时稳定在0附近。因此,本文所提出的新型趋近律全局快速终端SMC方法，其位置跟踪精度高，鲁棒性强。

图3 正弦波信号位置跟踪曲线

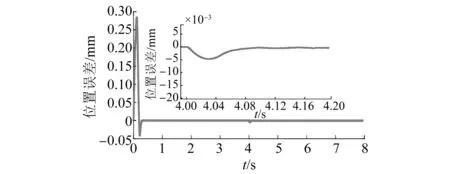
图4 正弦波下传统幂次趋近律位置误差曲线

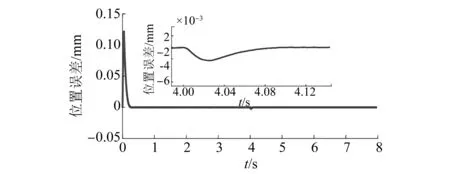
图5 正弦波下本文所提方法位置误差曲线

4.2 输入位置信号为阶跃信号

位置给定信号为1.5 mm，保持其他参数不变的情况下，在3 s时给定外部扰动，为40 N。本文提出的控制算法与传统幂次趋近律控制算法位置跟踪曲线如图6所示。从图6可以看出，本文提出的控制方法在0.3 s跟踪到给定位置信号，而传统幂次趋近律控制算法在0.1 s有一个跳跃在0.5 s跟踪到给定位置信号，本文提出的控制方法时间响应更快。

图6 阶跃信号控制系统位置跟踪曲线

基于传统幂次趋近律控制方法与本文提出的控制方法所设计的位置控制器，其位置误差曲线图如图7和图8所示。从图7可知，当系统突加40 N外部扰动时，基于传统幂次趋近律控制算法的位置误差迅速增大到6 mm，在4.14 s时能跟踪到给定位置信号。从图8可知，本文提出的控制算法在4 s加外部扰动时，位置误差增大到3.8 mm，最终在4.12 s跟踪到给定位置，且平稳运行。通过图7与图8可知，本文提出的控制算法在突加外部扰动时位置误差更小，跟踪位置响应速度更快。

图7 阶跃信号下传统幂次趋近律位置误差曲线

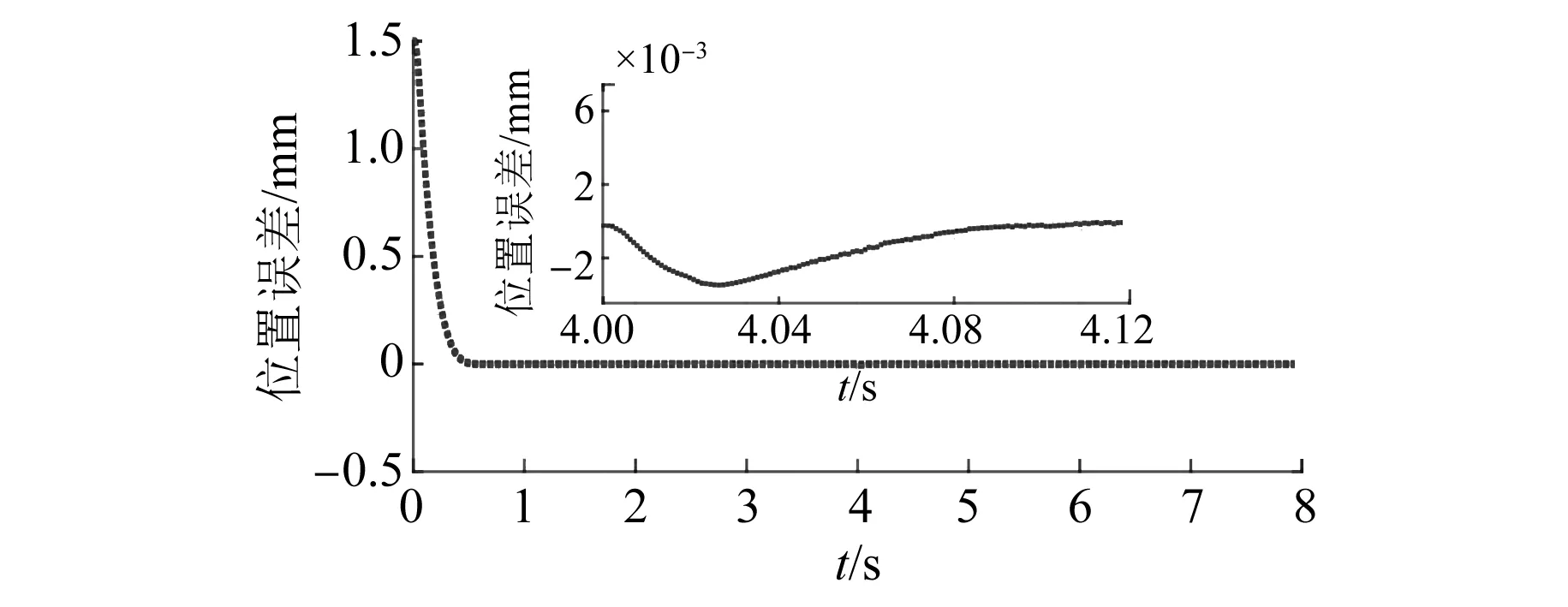
图8 阶跃信号下本文所提方法位置误差曲线

4.3 输入位置信号为梯形波信号

选取周期为2 s的梯形波参考轨迹作为位置输入信号，如图9所示。基于传统幂次趋近律控制方法与本文所提出的方法，位置跟踪的误差曲线如图10和图11所示。从图10可以看出，基于传统幂次趋近律控制方法位置误差在-0.08～0.11 mm。从图11可以看出，本文提出的控制方法位置误差在-0.03～0.08 mm。由此说明本文提出的控制方法具有更好的鲁棒性，位置误差也较小。

图9 输入位置给定信号

图10 梯形波下传统幂次趋近律位置误差曲线

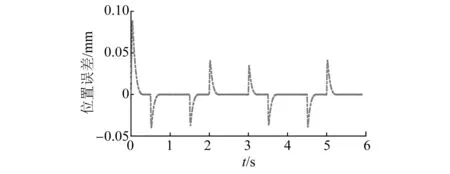
图11 梯形波下本文所提方法位置误差曲线

5 结 语

针对同时具有参数变化和外部负载扰动特性的PMLSM位置伺服控制系统，为了改善其位置伺服控制系统的性能，本文主要利用改进的滑模趋近律设计PMLSM伺服系统的位置控制器。由于外部的负载和扰动变化等不确定因素带来的影响，设计干扰观测器，对外部扰动进行估计，通过前馈补偿减少误差。用李雅普诺夫函数证明了控制器设计的合理性和系统稳定性，并证明了其在有限时间内收敛。通过仿真分析，与传统幂次趋近律控制方法相比，本文所提新型滑模趋近律控制方法，有效地提高了系统的位置跟踪精度和响应速度，增强了系统的抗扰动性能。