不同定权模型对GPS/BDS/Galileo短基线相对定位的影响分析

崔 琛

（1.河南省有色金属地质矿产局第七地质大队，河南 郑州 450016）

全球导航卫星系统（GNSS）是当前各方面建设不可或缺的服务系统。在各国不断建设发展自己的导航定位系统的同时，如何提升导航定位精度是当前研究的重点问题[1-3]。对各项误差改正模型进行改进以及正确选择定权方式均可有效提升定位精度[4-6]。相对定位是一种精密定位技术，尤其是短基线相对定位技术应用十分广泛；随着GNSS的蓬勃发展，多系统组合相对定位将是今后发展的趋势，而正确选择短基线相对定位定权模型是保证短基线相对定位精度的重要策略[7-8]。

对于定权模型的研究，国内很多学者做了相关工作，如孙鹏[9]分析了等权模型、高度角模型、信噪比模型以及信号强度模型对BDS定位精度的影响，得到信噪比模型和信号强度模型定位精度较高，在两个跟踪站高差较大时，更适合使用高度角模型的结论；刘亚[10]等将SISER不同方式的卫星轨道与钟差加入高度角定权模型，通过仿实时精密单点实验验证发现，该模型收敛时间减少了约0.91%，静态精密单点定位（PPP）精度可达厘米级甚至毫米级；吕明慧[11]等联合高度角和信噪比建立了全球化精细随机模型，将该模型应用于高纬度PPP解算中，其定位精度比传统的高度角和信噪比模型均有明显提升，尤其是高程方向定位精度提升更明显；钱妮佳[12]等提出了一种改进的信噪比随机模型，并采用改进的随机模型进行伪距单点定位解算，得到该模型的定位精度优于现存的几种模型的结论；伍劭实[13]等提出了一种根据不同模型实时组建观测量的随机模型，该模型能真实反映各卫星观测量的随机噪声特性，模糊度固定率和相对定位精度均有提升，更适合混合星座的BDS定位；蒋欠欠[14]等对比分析BDS、GPS、BDS/GPS系统在等权模型、高度角模型以及Helmert方差分量模型中的伪距PPP发现，组合系统定位精度优于单系统，Helmert方差分量模型定位精度最高，高度角模型次之，等权模型最低。综上所述，国内学者对定权模型的研究主要集中在伪距与PPP方面，缺乏对相对定位的研究，因此本文以一组约10 km的短基线数据为实验数据，对比分析了GPS、BDS、Galileo以及不同组合采用信噪比模型、高度角模型以及等权模型的相对定位精度。

1 数学模型

1.1 双差定位模型

双差定位模型是短基线相对定位的常用模型，一般表达式为[15-16]：

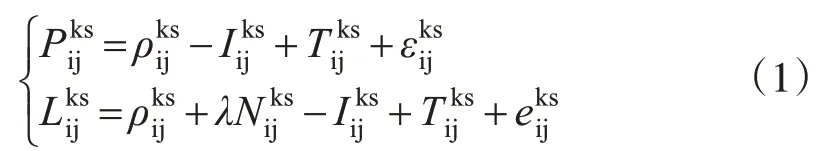
式中，s为参考卫星；k为非参考卫星；i为参考测站；j为非参考测站；为双差伪距观测值；为双差载波相位观测值；为测站至卫星间双差几何距离；λ为非参考星信号波长；为双差整周模糊度；为双差电离层延迟误差；为双差对流层延迟误差；为双差伪距观测值噪声；为双差载波相位观测值噪声。

1.2 等权随机模型

假设每颗卫星观测值的精度相同且独立，方差为σ0，构造n-1阶方差—协方差矩阵，即

等权随机模型可进一步表示为[14]：

式中，E为单位矩阵。

1.3 高度角随机模型

高度角随机模型就是对具有不同高度角的观测值进行方差估计而得到的一种的验前随机模型。首先，计算得到站心坐标下E、N、U方向的坐标，计算公式为：

式中，L0、B0分别为测站的经纬度；(Xs，Ys，Zs)、(X0，Y0，Z0)分别为卫星和测站的空间直角坐标。

然后，求得卫星与测站之间的卫星高度角，计算公式为：

最后，利用正弦三角函数公式对不同高度角卫星的观测值方差进行估计[14]，即

式中，E为卫星高度角；σ0为单位权方差。

1.4 信噪比随机模型

采用信噪比建立的观测值方差函数模型的一般表达式为：

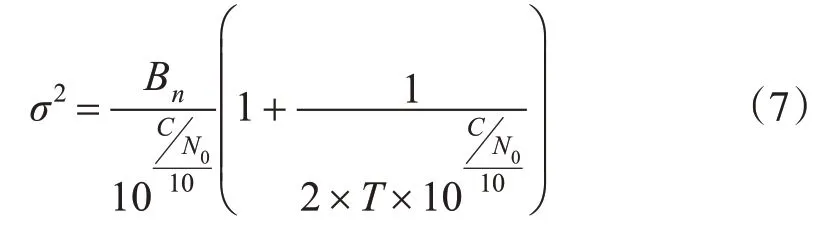
式中，Bn为载波相位跟踪环的宽度值；T为一体化检波的时间。

由于噪声量级非常小，对式（7）进一步简化，可得：

式中，Cn主要取决于接收机跟踪通道得到的相位跟踪环的宽度值；为信噪功率密度比值。

2 实验分析

2.1 数据选取与解算策略

为详细分析不同定权模型对短基线相对定位精度的影响，本文选取位于澳大利亚境内的两个MGEX站组成的一组短基线作为实验数据，测站分别为STR1和TID1站，基线长度约为10 km，数据采集时间间隔为30 s，采集时间为2021-04-21—2021-04-25。STR1站接收机类型为SEPT POLARX5，天线类型为ASH701945C_M；TID1站接收机类型为SEPT POLARX5，天线类型为AOAD/M_T；两个跟踪站均能接收GPS、BDS、Galileo信号。

数据解算软件采用Net_Diff软件，解算定权模型分别采用高度角定权、信噪比定权和等权模型，参与解算的GNSS系统分别为BDS、GPS、Galileo、BDS/GPS、BDS/Galileo、GPS/Galileo以及BDS/GPS/Galileo。

2.2 卫星可见性分析

各系统的卫星可见数如图1所示，可以看出，双系统组合卫星可见数多于任一单系统，三系统组合卫星可见数又多于双系统组合；BDS平均卫星可见数为7颗，主要受限于接收机类型，GPS平均卫星可见数为8颗，Galileo平均卫星可见数为5颗，BDS/GPS组合平均卫星可见数为15颗，BDS/Galileo组合平均卫星可见数为15颗，GPS/Galileo组合平均卫星可见数为12颗，BDS/GPS/Galileo组合平均卫星可见数为20颗。各系统的PDOP值如图2所示，可以看出，BDS和Galileo单系统的PDOP值较差，大部分历元PDOP值大于3；双系统和三系统组合卫星PDOP值较单系统有明显改善，尤其是BDS/GPS/Galileo组合全部历元的PDOP值均在2以内，平均PDOP值为0.87。

图1 各系统卫星可见数统计

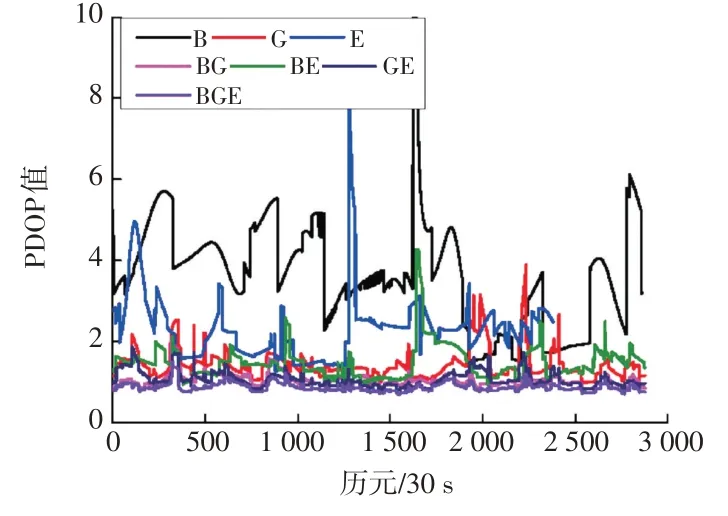
图2 各系统PDOP值统计

2.3 定位精度分析

本文对不同解算策略的解算结果进行统计，以2021-04-23的解算结果为例，各系统采用高度角模型、等权模型和信噪比模型解算的基线误差序列如图3～9所示，可以看出，单系统短基线相对定位误差较大，BDS与Galileo单系统短基线水平误差部分历元大于10 cm，甚至更大，部分历元高程方向误差大于20 cm，甚至更大，GPS单系统除部分历元外，水平定位误差在±5 cm以内，高程定位误差在±10 cm以内；双系统组合定位误差较单系统有明显减少，除少部分历元外，水平定位误差在±5 cm以内，高程定位误差在±10 cm以内；三系统组合定位误差又较双系统有所减少，水平定位误差在±5 cm以内，高程定位误差在±10 cm以内；采用高度角模型解算的基线结果定位误差较稳定且较小，其次为信噪比模型，等权模型定位误差略大。

图3 BDS单系统不同定权模型短基线解序列

图4 GPS单系统不同定权模型短基线解序列

图5 Galileo单系统不同定权模型短基线解序列

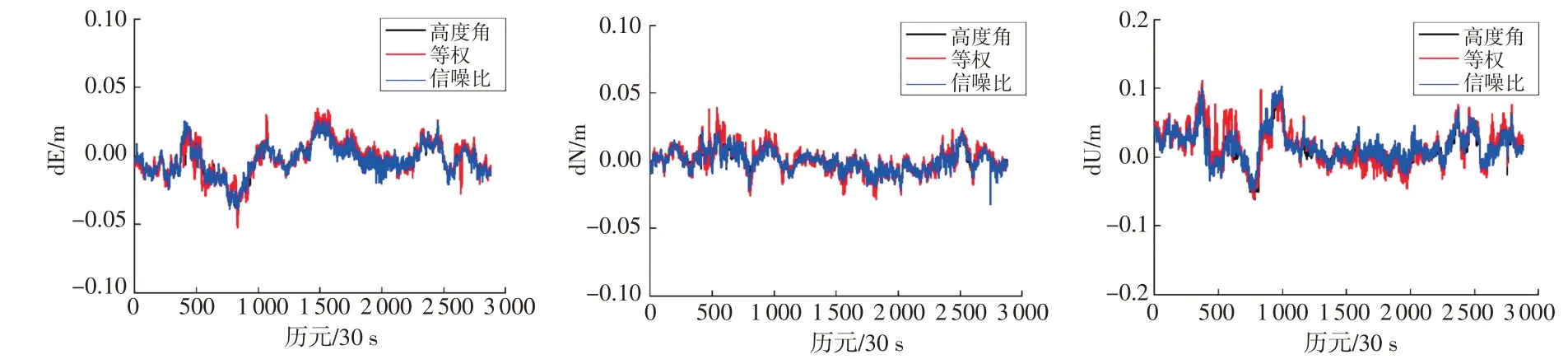
图6 BDS/GPS组合不同定权模型短基线解序列

图7 BDS/Galileo组合不同定权模型短基线解序列

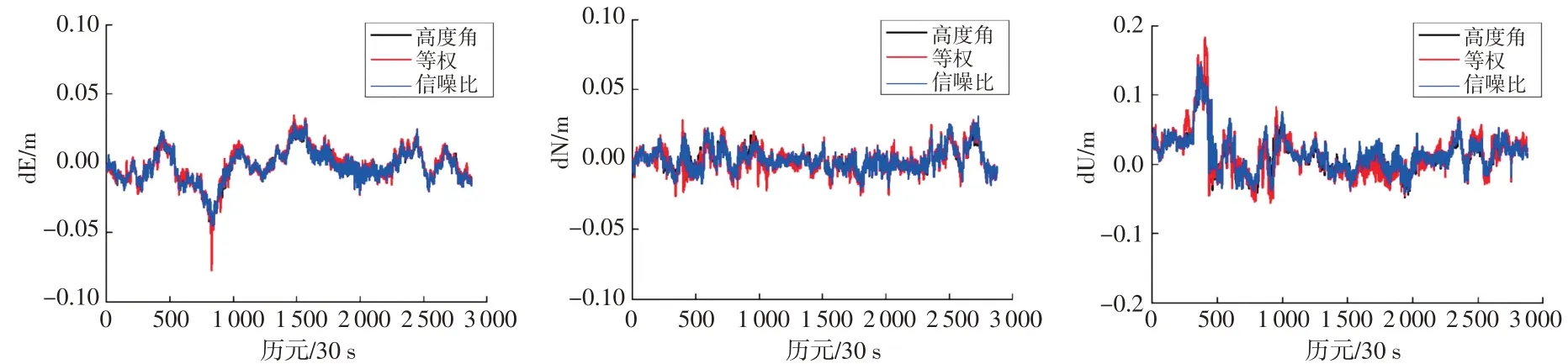
图8 GPS/Galileo组合不同定权模型短基线解序列

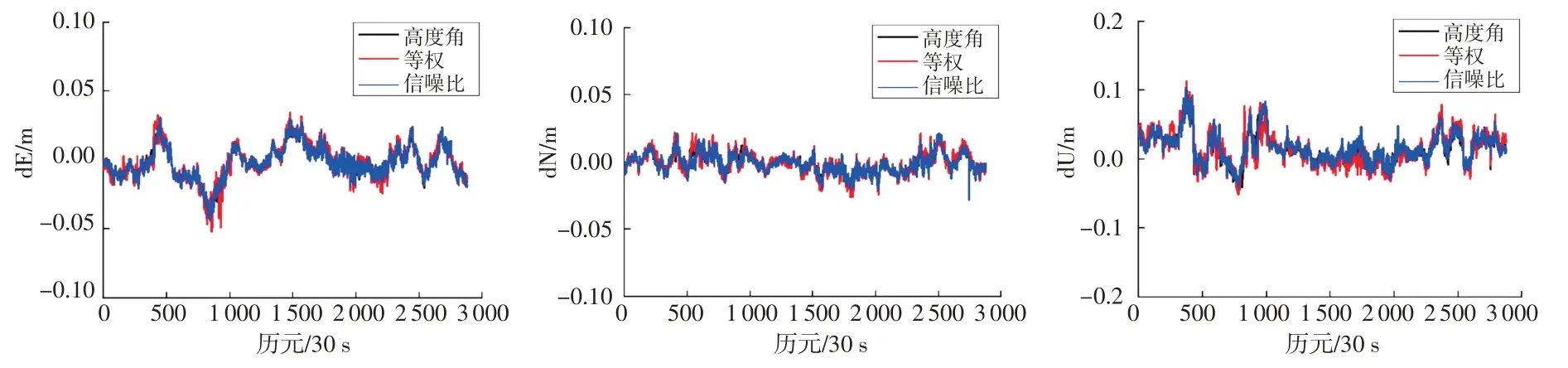
图9 BDS/GPS/Galileo组合不同定权模型短基线解序列

为更加详细分析不同定权模型对短基线相对定位精度的影响，本文进一步统计各系统采用高度角模型、等权模型以及信噪比模型解算的基线解多天定位精度，如图10所示，可以看出，采用等权与信噪比模型解算的短基线定位结果略差，采用3种模型解算的短基线定位精度均低于其他系统，其余情况定位精度较好；E方向定位精度优于2 cm，N方向定位精度除GPS个别情况外均优于1 cm，U方向定位精度除等权模型外均优于3 cm，基线中误差在4 cm以内；采用高度角模型解算的定位精度最优，信噪比模型次之，等权模型最差。

图10 不同定权模型定位精度平均值

2.4 多系统组合较单系统定位精度提升定量分析

为进一步对比多系统组合较单系统短基线相对定位的优势，本文进一步统计了双系统和三系统组合相较于单系统定位精度的提升量平均值，如表1所示，可以看出，在3种定权模型下，双系统和三系统组合较单系统定位精度均有明显提升，尤其是三系统组合定位精度提升较明显；对于高度角模型，三系统组合比BDS单系统定位精度在E、N、U方向分别提升了7.32%、13.16%、10.32%，比GPS单系统定位精度在E、N、U方向分别提升了2.56%、30.53%、23.39%，比Galileo单系统定位精度在E、N、U方向分别提升了72.40%、70.40%、73.51%；对于等权模型，三系统组合比BDS单系统定位精度在E、N、U方向分别提升了76.78%、72.38%、59.97%，比GPS单系统定位精度在E、N、U方 向 分 别 提 升 了10.79%、34.71%、23.29%，比Galileo单系统定位精度在E、N、U方向分别提升了75.25%、72.85%、69.09%；对于信噪比模型，三系统组合比BDS单系统定位精度在E、N、U方向分别提升了48.20%、46.88%、44.22%，比GPS单系统定位精度在E、N、U方向分别提升了2.54%、29.90%、23.59%，比Galileo单系统定位精度在E、N、U方向分别提升了70.21%、69.09%、75.48%；采用3种定权模型的双系统和三系统组合定位精度相较于GPS和Galileo单系统提升量相当，采用等权模型的双系统和三系统组合定位精度比BDS单系统提升量最大，采用信噪比模型次之，采用高度角模型最小。

表1 多系统组合相较于BDS、GPS、Galileo单系统定位精度的提升/%

综合表1和图10分析可知，Galileo单系统短基线定位精度较差，更适合与其他系统组合进行定位，而BDS和GPS单系统短基线精度相当且较高；定权模型对GPS和Galileo单系统和与其他系统组合定位性能的影响较小，对BDS单系统和与其他系统组合定位性能的影响较大。

3 结语

针对短基线相对定位解算定权模型的选择问题，本文基于一组实测短基线数据，详细分析了高度角模型、等权模型和信噪比模型在BDS/GPS/Galileo短基线相对定位解算中的应用，得到的结论为：①多系统组合能有效改善单系统卫星可见数较少和PDOP值过大的情况；②除个别情况外，BDS单系统短基线定位精度较优，定位精度可达厘米级，而Galileo单系统定位精度较差，双系统和三系统组合定位精度较单系统均有明显提升，尤其是三系统组合定位精度最为明显，可为今后短基线相对定位系统选择提供一定参考；③3种定权模型中，高度角模型定位精度最优，信噪比模型次之，等权模型定位精度最低，可为今后短基线相对定位定权模型选择提供一定参考；④定权模型对GPS、Galileo及其相关组合定位影响较小，而对BDS及其相关组合定位影响较大。