服务创新驱动下物流服务供应链纵向整合策略
——基于链间竞争视角
2022-11-25张小蒙赵启兰张建军
张小蒙,赵启兰,张建军
(1.北京交通大学 经济管理学院,北京 100044;2.内蒙古农业大学 经济管理学院,内蒙古 呼和浩特 010010 )
一、 引 言
纵向整合是一种有效且重要的企业战略,是多数企业规模发展到一定程度采用的重要战略[1]。纵向整合由纵向一体化演变而来,但在实现模式上更加多样化,在纵向整合的实现上,学者们普遍认为投资自建、兼并、收购控股和入股是其主要方式[2]。随着物流服务经济的迅速发展,物流企业间竞争强度的增大,已有部分物流服务企业为进一步提升核心竞争力,将物流服务供应链(Logistics Service Supply Chain,LSSC)进行纵向整合(Vertical Integration)[3]。例如,在航运物流服务企业中,港口企业、航运公司等在内的各环节成员组建纵向联盟,共同对某一综合物流项目进行投资和建设,例如鹿特丹港与石化行业中的巨头组建石化战略联盟。基于供应链管理的视角,物流企业竞争日益表现为所在的物流服务供应链之间的竞争。物流企业要在新一轮竞争浪潮中取得领先地位,不仅要考虑自身供应链的整合决策,还要时刻关注外部竞争者的整合决策[1]。因此,物流企业如何在供应链竞争的环境下获取竞争优势,是实现盈利增长的关键保证。
在大数据背景下,现在越来越多的物流服务企业注重服务创新的提升,通过提高客户服务创新体验来提高自身的竞争力[4-5]。以菜鸟、京东、顺丰为主的物流服务企业,利用大数据技术对物流服务过程进行优化和重构,为客户提供创新性的物流服务体验。生鲜电商多点(DMALL)通过与本地大型商超的深度合作打造线上线下一体化的全渠道零售平台,可以为顾客提供高品质、低价格、2小时送达的优质服务。每日优鲜基于顾客对生鲜农产品购买的“即时性”消费需求,在物流配送中采取了前置仓的服务创新模式[6]。京东终止了与天天快递和百世快递的合作,理由是“综合服务质量较差,违反平台规则”,京东这一举措表明,大数据时代物流服务创新水平已成为物流企业的竞争点。
大数据时代,互联网技术的不断成熟使得物流服务企业的服务创新更容易实现,物流服务的创新极易引发利益和资源冲突,也会对供应链的整合决策产生影响。例如,京东利用自身数据优势,为客户提供创新性的物流服务体验,最终选择了终止与天天快递和百世快递的合作。而作为阿里巴巴旗下数据驱动的社会化协同平台,菜鸟网络在服务创新驱动下最终选择与百世快递为代表的物流服务提供商进行纵向整合。京东和菜鸟面对的是同一个物流市场,均在服务创新驱动下面对同一个物流服务市场,为什么京东和菜鸟选择的整合决策不同?物流服务创新是怎么影响物流服务企业的整合决策的?物流服务创新水平能对整合决策影响多少?这些企业的战略决策是否最优?而在理论方面,通过文献的整理,关于服务创新对供应链整合决策影响的相关研究中,关于服务创新对单条供应链影响的文献较多,主要相关文献内容在本文第二部分文献综述中详细讲述。在链与链之间存在竞争情况下,创新对供应链整合决策影响的文献较少。李晓静等(2018)基于竞争供应链市场,研究了供应商采取技术创新,制造商为主导企业,零售商是完全价格竞争背景下,制造商进行前向一体化或后向一体化的结构选择问题[1]。而当核心企业本身处于竞争环境时,供应链成员采取技术服务创新对供应链的整合决策会产生哪些影响?因此,在前人研究思路基础上,本文研究了服务提供商采取服务创新,核心企业本身在完全价格竞争情况下的物流服务供应链整合决策问题。深入研究服务创新驱动下,竞争物流服务供应链纵向整合决策发生和存在条件以及对整个物流服务供应链运营效率的影响,对进一步探索竞争物流服务供应链纵向整合的决策选择提供了重要的理论基础。
二、 文献综述
在本节中,本文从传统供应链(制造商零售商)和物流服务供应链角度,回顾了有关供应链竞争和服务创新投资对供应链整合决策影响的相关文献。对传统供应链的回顾从两个角度来看。第一个问题是关于供应链存在竞争时利益相关者之间的合作;另一个问题是服务创新对供应链的整合决策影响。
(一) 供应链竞争相关研究
围绕供应链竞争的研究较多,并且形式更加多样,主要研究问题分为两个方面,第一是关于内部供应链中的利益相关者之间的合作。鲁其辉和朱道立(2009)基于研究需要,构建了在产品质量及价格方面均存在竞争的供应链,对无协调情境、协调情境和混合情境下的情况进行比较分析,发现协调策略并非总占据优势,也有可能陷入囚徒困境[7]。王玉燕等(2021)的研究发现在三级电商供应链中,无论制造商或零售商哪一方处在主导地位,都能够获得更高的利润,优化Shapley值法协调后得出的集中决策模式要优于上述两种情况,此时各节点企业的利润对于供应链中产品质量与服务水平变动情况具有较高的敏感度[8]。申成然和刘小媛(2019)探讨了碳减排努力程度与供应链有关企业的风险规避程度对供应链产品价格决策方面的影响[9]。He等(2022)探讨了电子商务平台服务供应链的物流整合问题,该供应链由制造商、电子商务平台及第三方物流服务公司组成,目的是分析制造商渠道对物流整合以及整个供应链的影响[10]。虽然这些文献在理论体系和模型方法上相对丰富和成熟,有助于本文基于物流服务供应链的竞争进行分析,但这些问题不是本文的研究重点。供应链竞争的另一个研究问题是本文的重点关注问题:两条供应链之间存在竞争时利益相关者之间的合作。江志娟与董千里(2015)探讨了制造业同物流业之间的竞合关系,认为制造业同物流业的合作研究应以产品链与物流服务链之间的关系研究未来发展方向[11]。张学龙等(2018)探讨了包含一个制造商与两个具有竞争关系的零售商构成的供应链协调决策问题,发现无论采用哪种决策模式,服务质量都与供应链中的服务替代系数成反向比例关系[12]。以上文献关于供应链竞争的整合决策研究背景主要集中于产品供应链之间竞争,产品供应链与服务供应链之间双渠道的竞争。与他们不同,本文的研究问题是基于相互竞争的物流服务供应链视角下研究整合决策。本文认为物流业中存在货运价格的竞争,而物流服务供应链就是服务链,客户会注重服务体验。因此,本文建立了一个上游服务提供商进行服务创新投资,下游集成商存在价格竞争的Stackelberg模型来描述物流服务供应链的主要特性。
(二) 服务创新对供应链整合决策影响相关研究
目前围绕服务创新对供应链整合决策影响的研究主要包括两个方面:第一是主要关注服务创新对于单条供应链整合决策的影响。Wang等(2021)探讨了由投资创新的供应商和向用户销售产品的制造商组成的供应链,创新增加了产品对用户的价值,分析一个讨价还价模型,发现供应商对创新的投入程度与供应商的议价能力相关[13]。Guptar和Loulou(1998)对供应链的创新决策问题与过程创新问题进行了分析,探讨了产品差异化情况对制造商整合结构选择决策的影响[14]。Ching-Chiao(2012)的研究证实了物流服务的创新能够促进制造商与供应商之间的交流,增进两者之间的战略伙伴关系[15]。杨丽等(2019)探讨了三级供应链模式下,物流服务商参与产品价格与物流服务价格的最优决策问题,并探讨了能力创新在物流服务供应链合作中发挥的作用[16]。Lii和Kuo(2016)探讨了创新导向与供应链整合等因素对企业绩效的影响,收集了来自台湾电子工业公司的480份有效问卷,运用结构方程模型对收集到的数据进行了分析,结果发现创新导向能够对供应链整合以及企业绩效产生正向影响,为创新导向对供应链整合的影响分析提供了实证支持,并基于资源依赖理论表明了创新导向帮助企业整合供应链的潜力[17]。Tomas等(2022)考察了供应商创新对供应链整合与可持续绩效的影响,以及供应链整合是否在供应链创新与可持续绩效间具有中介作用,将信任作为供应商创新的决定因素构建了结构方程模型,结果验证了信任是关键供应商创新的决定性因素,供应商创新能力对供应链整合与可持续性绩效具有直接影响,但是当模型中引入供应链集成时,上述影响消失[18]。服务创新对供应链的影响研究的第二个问题是,关于在链与链存在竞争情况下服务创新对供应链整合决策的影响。李晓静等(2018)基于竞争供应链市场,研究了制造商采取技术创新,零售商处于竞争市场,单一制造商作为核心企业如何进行整合决策的问题[1]。而现实中在非垄断情况下,核心企业与核心企业间往往是相互竞争的。因此本文在前人的基础上,研究服务创新驱动下,核心企业本身在完全价格竞争情况下的两条平行竞争的物流服务供应链纵向整合决策问题。
(三) 物流服务供应链整合决策相关研究
物流服务供应链是纵向整合发生的载体,学术界对供应链整合的研究成果很多,范围也很广[19-21]。近年来,在物流服务供应链整合决策中逐渐考虑了竞争的影响。郭英等(2022)对一个物流服务集成商构成的供应链系统及两个物流服务提供商竞争的供应链系统进行了分析,将研究视角聚焦在物流服务供应链进行纵向整合问题,以物流服务质量成本为基础,构建了纵向分散模式与纵向整合模式下的质量博弈模型,以分析纵向整合策略对于物流服务供应链实际运作效率产生的影响;结果发现竞争强度对供应链中的企业决策与策略选择具有重要影响,实施纵向整合策略后,接受整合的物流服务提供商将会产生协同效应,同时对未参与整合的物流服务商产生外部效应;只有在竞争强度较大的情况下,物流服务集成商与提供商均会做出纵向整合的决策,以提高整体物流服务水平,降低优化物流服务质量的现实成本[2]。冯颖和顾佳美(2016)对TPL主导模式下生鲜农产品的供应链物流水平最佳决策问题进行了探讨,构建了TPL/供应商主导模式下用于决定最优决策的序贯非合作博弈模型,结果发现供应商主导模式下的物流服务水平与订购量更优,TPL主导致使自身利润增加而供应链其他成员利润减少;并在上述研究结论的基础上,提出引入物流成本共担与收入共享契约来达成供应链协调发展的目的[22]。张建军和赵启兰(2019)探讨了两级物流服务商参与模式下的供应链最优决策问题,对不同决策模式下得出的最优决策进行了比较分析,提出了零售商适用的最优局部合作决策,对价格外生性和有关敏感系数对于供应链最优决策产生的作用进行了分析,结果发现局部合作决策能够在一定程度上达成供应链利益的协调;并探究了包含两级物流服务商的双渠道供应链系统如何进行最优决策和利益协调的问题,结果发现PSC集中决策能够优化综合体验服务水平,而LSSC集中决策能够优化物流服务水平[23]。以上文献讨论的是内部竞争而不是外部竞争。还有文献是从供应链整合的角度,研究了物流服务供应链的链间竞争。如刘家国等(2021)基于港口服务竞争条件下构建了三级航运供应链,对承运商的纵向整合决策问题进行研究,结果发现港口服务的竞争程度对承运商向前整合决策的选择具有决定性影响,港口服务投入系数对承运商的后向整合决策具有决定性影响[24]。刘华明和王勇(2017)的研究验证了3PL服务能力对于供应链整合产生的影响,结果发现3PL服务能力能够对外包企业的供应链产生显著正向影响,同时3PL的增值能力也显著影响着外包企业的内部整合与客户整合,并且影响程度远大于其他基本能力的影响,为企业的供应链纵向整合管理提供了理论参考[25]。Shen等(2019)构建了包含物流服务商的跨境供应链,对两种去留服务领导权模式下跨境供应链中的产品价格与物流服务水平决策问题进行了研究,强调了物流服务商在跨境供应链中参与决策的重要性[26]。不同的是,本文通过构建两条平行竞争的物流服务供应链,建立链间Nash竞争和链内成员Stackelberg博弈模型,链内上游物流服务提供商提高服务创新水平和下游物流服务集成商存在价格竞争情况。此外,本文还发现在一定条件下,两个物流服务供应链采取相反决策时,利润是双赢的。更有趣的是,本文发现在一定条件下,两条物流服务供应链可能存在囚徒困境的状态。
三、 问题描述与基本假设
为了提高客户的物流服务体验,物流服务提供商要对物流服务进行服务创新投资,而物流服务集成商处在完全价格竞争的市场中,面临着同类企业的价格竞争压力,在提供商进行服务创新的驱动下,是否对物流服务提供商采取整合策略?因此本文构建了两条平行竞争的两级物流服务供应链(Logistics Service Supply Chain,LSSC),其中每条链均由一个物流服务集成商(Logistics Service Integrator,LSI)和一个物流服务提供商(Logistics Service Provider,LSP)构成。两条物流服务供应链面向同一个物流服务市场。例如,货拉拉和快狗所在的供应链面向同一类市场构成相互竞争的关系。货拉拉电商平台所在的供应链中,物流服务集成商是指货拉拉平台,物流服务提供商是指提供车辆运输服务的社会个人企业;快狗电商平台所在的供应链中,物流服务集成商是指快狗平台企业,物流服务提供商是指嘉里物流企业。再比如,菜鸟和顺丰所在的供应链面向同一类市场构成相互竞争的关系。在菜鸟所在的供应链中,物流服务集成商是指菜鸟,物流服务提供商是圆通、申通等物流企业;顺丰所在的供应链中,物流服务集成商是指顺丰,物流服务提供商有可能是中铁快运等物流服务企业。每一条二级物流服务供应链均可以选择不整合或整合,对应着两种LSSC结构:分散式(D)和集中式(C)。当LSSC选择不整合决策时,对应的是分散结构,LSSC内部的LSP和LSI之间会进行Stackelberg博弈,各自均按照自身利润最大化来决策;当LSSC选择整合决策时,对应的是集中结构,LSSC将会以LSI为核心来对外提供一整套物流服务。因此,两条LSSC(令i为1,2)的不同整合决策在理论上会产生四种LSSC结构组合:CC模式(两条LSSC均选择整合)、CD模式(LSSC1选择整合,LSSC2选择分散)、DC模式(LSSC1选择分散,LSSC2选择整合)、DD模式(两条LSSC均选择分散),如表1所示。

表1 两条二级LSSC的四种结构组合
假设两条二级LSSC之间的竞争模式为Nash竞争,即LSSC1和LSSC2之间是对等的议价权力或市场地位,具体表现为两条链将同时做出各自的最优决策。由于整合模式的对称性,模式CD和DC在竞争结构上是互相对称的,因此,本文只考虑三种二级LSSC竞争模型,分别命名为:双集中模型(CC)、混合模型(CD)和双分散模型(DD),如图1所示:图中虚线框代表集中结构,采取整合决策。
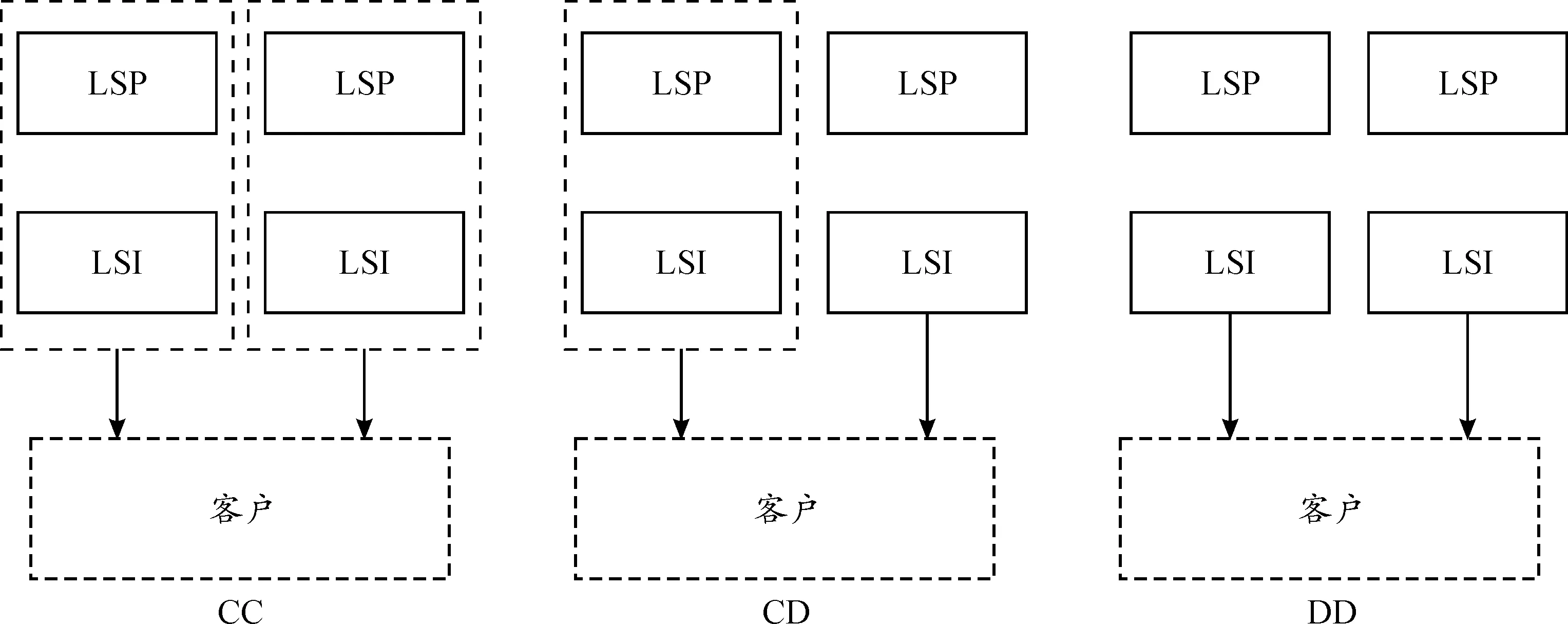
图1 服务创新驱动下的竞争模型
当供应链成员为集中结构时,供应链成员LSP与LSI共同决定服务创新投资水平和提供给客户服务的价格。当供应链成员为分散结构时,供应链成员间为Stackelberg动态博弈,决策顺序是:LSP先决定服务创新投资水平和物流服务批发单价,然后LSI为最大化自身利润,再面对市场决定提供给客户服务的价格。根据李晓静等(2018)[1]的创新驱动下的供应链模型及刘家国等(2021)[27]的服务竞争供应链模型,本文将LSSCi的物流服务需求函数设定为:
qi=a-pi+up3-i,i=1,2
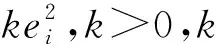
此外,本文假设LSI的单位运营成本为cLSI,LSP的单位运营成本为cLSP,并且LSP和LSI之间是信息对称且均为风险中性,但两条LSSC之间合同不可预见。在优化求解时,本文只将参与整合的双方视为一个整体,不考虑整合体内部的具体利润分配形式。
本文所涉及的符号及其含义如表2所示。

表2 变量及符号描述
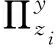
四、 不同整合决策模式的决策情况
(一) 双集中模型(CC)
在CC模型下,两条LSSC均选择整合决策,其结构均为集中式。具体博弈过程如下:两条LSSC均选择集中式结构,LSPi和LSIi共同决定对外提供的服务创新投资水平ei和物流服务单价pi,以实现LSSCi整体利润的最大化。容易得到,在集中结构下链i的目标利润函数为:
(1)
将需求函数代入,对ΠLSSCi进行最优化求解,为计算便利本文特定b=1[27],ΠPi关于pi和ei的一阶偏导数为:
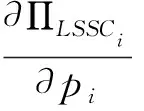
(2)

(3)
故令式(2)和(3)均等于零,联立求解可得最优化链i的均衡解,代入其目标利润函数,求得其最优利润,即可得到如下命题。
命题1:在物流市场潜在基本需求、物流服务集成商和服务提供商的单位经营成本、服务创新成本系数、链间竞争强度均给定时,即在给定参数a,cLSI,cLSP,k和u时,CC竞争模型的最优结果如下。
(1)均衡解为:
(4)
(5)
(6)
(2)两个LSI的利润,亦即两条LSSC的最优利润为:
(7)
(二) 混合模型(CD)
在链间Nash竞争下,由于结构的对称性,混合竞争结构CD和DC本质上属于同一种结构类型,均为一条LSSC选择分散式而另一条LSSC选择集中式。为了不失一般性,假定LSSC1采取集中式结构,即LSI1与LSP1互相整合,作为一个整体共同为物流服务市场提供“一站式”服务;LSSC2采取分散式结构,即LSP2为其下游客户提供物流服务,决定提供的物流服务水平,LSI2决定客户的物流服务市场价格,LSP2与LSI2共同组成LSSC2。LSSC1与LSSC2之间发生横向Nash竞争,构成混合竞争模型(CD)。
具体博弈过程如下:第一阶段,LSP2决定其最优的传统服务批发单价h2和服务水平e2,提供给下游的LSI2;第二阶段,下游的LSI2决定物流服务市场单价p2,同时LSSC1的整合体共同决定其物流服务市场单价p1和服务水平e1,最终实现各成员的利润最大化。由此可以得到,在混合结构下LSSC1和LSSC2的目标利润函数分别如下:
LSSC1的目标函数为:
(8)
LSSC2的目标函数为:
(9)
ΠLSI2=(p2-h2-cLSI)q2
(10)
将需求函数代入,采用逆向推导法求解两条LSSC各自的目标利润函数。首先对ΠC2进行最优化,令ΠLSI2关于p2的一阶导函数为零,为计算便利本文特定b=1,得到p2关于h2和e2的反应函数。
(11)
同时对ΠP1进行最优化,求出ΠP1关于p1和e1的一阶偏导数,并令其为零,得到:
(12)
(13)
将p2的反应函数代入上游ΠP2中,再求出ΠP2关于h2和e2的一阶偏导数,令其为零,得到:
(14)
(15)
命题2:在物流市场潜在基本需求、物流服务集成商和服务提供商的单位经营成本、服务创新成本系数、链间竞争强度均给定时,即在给定参数a,cLSP,cLSI,k和u时,CD竞争模型的最优结果如下。
(1)均衡解为:
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(2)两条LSSC成员的最优利润分别为:
(23)
(24)
(25)
(3)继而两条LSSC的总最优利润分别为:
(26)
(27)
混合结构DC和CD的均衡解和最优利润在数值上是互相对称的,此处便不再赘述。
(三) 双分散模型(DD)
当两条LSSC均选择不整合时,即LSP1与LSI1组成LSSC1,LSP2与LSI2组成LSSC2,两条链之间为横向Nash竞争,构成双分散竞争模型(DD)。具体博弈过程如下:LSPi决定其最优的物流服务批发单价hi和服务水平ei,LSIi为最大化自身利润,再面对市场决定各自的物流服务市场单价pi。
由此能够得出,在双分散结构下链i的目标利润函数如下:
(28)
ΠLSIi=(pi-hi-cLSI)qi
(29)
将需求函数代入,采用逆向推导法求解链i的目标利润函数。为计算便利本文特定b=1[27],首先对ΠLSIi进行最优化,令ΠLSIi关于pi的一阶导函数为零,得到pi关于hi和ei的反应函数。
(30)
将反应函数代入上游ΠLSPi中,再求出ΠLSPi关于hi和ei的一阶偏导数,令其为零,即得:
(31)
(32)
最终联立等式(30)、(31)和式(32),可得最优化链i的均衡解,代入其目标利润函数,求得其最优利润,即可得到如下命题。
命题3:在物流市场潜在基本需求、物流服务集成商和服务提供商的单位经营成本、服务创新成本系数、链间竞争强度均给定时,即在给定参数a,cP,cC,k和u时,DD竞争模型的最优结果如下。
(1)均衡解为:
(33)
(34)
(35)
(36)
(2)两条LSSC上的LSP和LSI的最优利润分别为:
(37)
(38)
(3)两条LSSC的总最优利润分别为:
(39)
五、 不同整合决策模式的利润比较分析
(一) 对手链选择不整合(D)时,自身链的利润比较
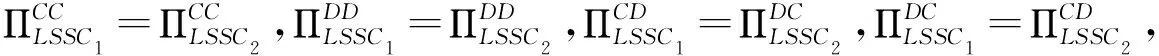
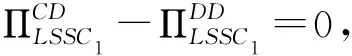
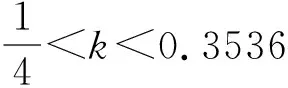
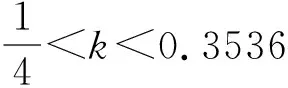

证明过程见附录(备索)。

图的关系图
由引理1可以得出,当快狗平台企业与嘉里物流企业采取分散决策不进行整合,服务创新系数较大时,无论两条链的价格竞争强度如何,货拉拉平台企业和参与的社会个人企业采取不整合决策可以使货拉拉链获得更高的利润;当服务创新系数较小,链间价格竞争强度较大时,货拉拉平台企业和参与的社会个人企业采取整合决策可以使货拉拉链的利润大于采取不整合决策的利润;当服务创新系数较小,链间价格竞争强度也较小时,货拉拉平台企业和参与的社会个人企业采取不整合决策比整合决策获得的利润更高。
由引理1可得出如下定理:
定理1:当对手LSSC选择不整合时,对于自身LSSC而言,整合与否取决于两条链之间的竞争程度和服务创新成本系数的范围。两个参数满足于:
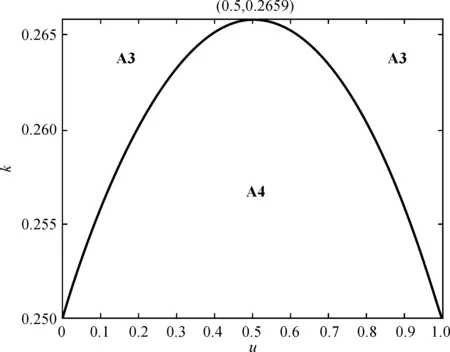
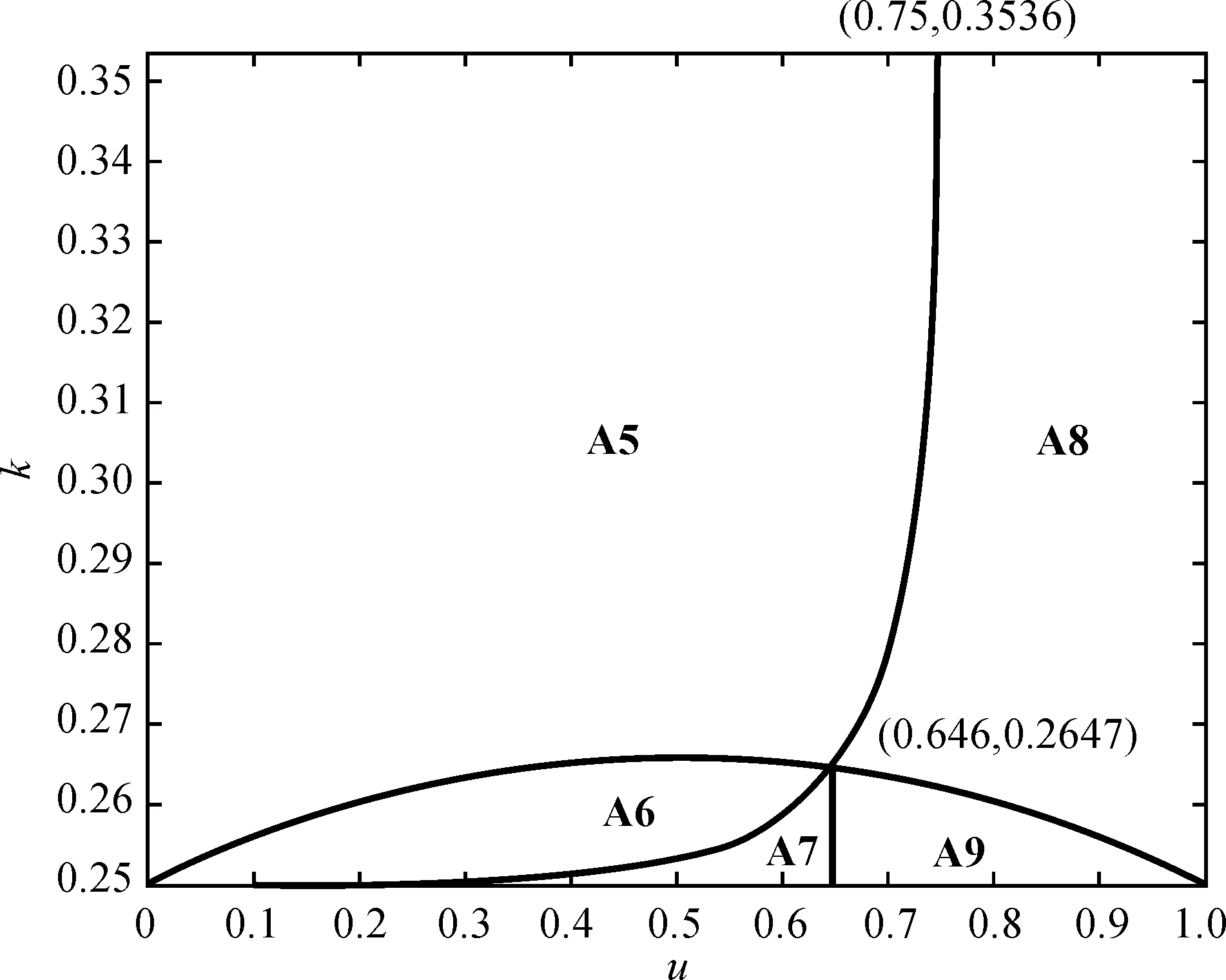
(i)当0.25 (ii)当0.25 (iii)当k≥0.3536时,0 定理1表明,当对手链选择不整合时,对于自身链上的LSI而言,是否选择与上游的LSP整合,会受到其服务创新成本系数k和链间竞争程度u的影响。当k较小时(0.25 证明过程与引理1类似。 由引理2可以得出,当快狗平台企业与嘉里物流企业采取分散决策不进行整合,当服务创新系数较大时,无论两条链的价格竞争强度如何,货拉拉平台企业和参与的社会个人企业采取不整合决策可以使快狗链获得更高利润。 当服务创新系数较小,链间价格竞争强度符合一定条件时,货拉拉平台企业和参与的社会个人企业采取整合决策可以使快狗链的利润大于采取不整合决策的利润。 当服务创新系数较小,链间价格竞争强度符合一定条件时,货拉拉平台企业和参与的社会个人企业采取不整合决策比整合决策使快狗链获得的利润更高。 图的关系图 由引理2可得出如下定理: 定理2:已知对手LSSC选择不整合,自身LSSC整合与否,将同样影响对手LSSC的整体利润的高低,同时其影响取决于两条LSSC之间的竞争程度和服务创新成本系数的范围。两个参数满足于: (i)当0.25 (ii)当0.25 (iii)当0.25 (iv)当0.25 (v)当k≥0.2659且0 定理2表明,在对手LSSC选择不整合的前提下,当LSI价格竞争程度和LSP服务创新成本系数发生变化时,自身LSSC会有不同的整合决策,其决策的变化同样会反过来影响到对手LSSC整体利润的大小。当对手链已确定为分散式结构时,如图3所示,在右上区域A3对应着较小的服务创新成本系数和较大的竞争程度,此时如果自身链选择不整合,其将会提升对手链的整体利润;而在区域A4对应着较小的服务创新成本系数和较小的竞争程度,此时如果自身链选择整合,反而会提高对手链的整体利润。当k较大时(k≥0.2659),对于自身链上的LSI而言,是否选择与上游的LSP整合使对手链利润更高,主要取决于服务创新成本系数,而与链间竞争程度的大小无关。即服务创新成本系数较大时,此时无论链间竞争程度如何,对自身链上的LSI而言,自身链均会倾向于不整合自身的上下游成员,使对手链利润更高。 图与的关系图 由图4中A5、A6区域可以看出,当链间竞争程度u较小,服务投入系数k处于一定范围时,在链2始终保持分散结构的前提下,当k逐渐增大时,即从区域A5到区域A6,链1始终保持着分散结构,使得其自身的总体利润得到一定的增长,但降低了对手链的利润。 从图4中A6、A7区域可以看出,当链间竞争程度u较小时,在LSSC2始终保持分散结构的前提下,当k逐渐减小时,即从区域A6到区域A7,可以表明,LSSC1的最优决策由分散式变为集中式时,集中式LSSC2的利润也会有所增长。因为随着服务创新成本系数k的减小,两条链的服务水平提升的门槛较小,服务创新带来的竞争力较弱,此时自身LSSC1为了获得额外的整合效益使自身更具竞争力,需要将内部的LSP和LSI整合为一体。在特定的(k,u)范围内,即区域A7,这种整合效益会产生一定程度的正外部性,使得对手LSSC2的整体利润也会得到一定程度的增长。 从图4中A8、A9区域可以看出,当链间竞争程度u较大时,随着k逐渐减小,即从区域A8到区域A9,自身LSSC1将继续维持整合措施,加强上下游的整合效益,此时整合措施给自身LSSC1带来的市场竞争优势将会大大超过其溢出的正外部性,反而在一定程度上压制了分散式LSSC2的市场竞争地位,因此对手LSSC2的利润将会出现下降。 由此可以得出如下推论: 推论1:当(k,u)处于某个特定范围时,在同一水平发生横向Nash竞争的两条物流服务供应链,当其中一条LSSC选择不整合时,另一条LSSC选择整合,不仅能提升自身的整体利润,还能影响对手LSSC整体利润,对手链利润的变化主要取决于竞争强度。 从图4中A5、A7、A9区域可以看出,当服务创新成本系数和链间竞争程度处于一定范围时,在LSSC2始终保持分散结构的前提下,LSSC1的最优决策A5区域为整合决策,A7、A9区域最优决策为不整合决策。但在A5、A7、A9区域LSSC1的最优决策总能达到双赢,即不仅能提高自身链的利润,还能提高对手链的利润。 推论2:当(k,u)处于某个特定范围时,在同一水平发生横向Nash竞争的两条物流服务供应链,当其中一条LSSC选择不整合时,另一条LSSC存在最优决策,不仅能提升自身的整体利润,还能促进对手LSSC整体利润的提升。 当快狗链选择整合(C)时,此时比较货拉拉链在CC结构和DC结构下的整体利润大小关系,可以得到如下引理: 证明过程与引理1类似。 由引理3可以得出,当快狗平台企业与嘉里物流企业采取集中决策进行整合,当服务创新系数较大时,无论两条链的价格竞争强度如何,货拉拉平台企业和参与的社会个人企业采取整合决策可以使货拉拉链获得更高利润;当服务创新系数较小,链间价格竞争强度也较小时,货拉拉平台企业和参与的社会个人企业采取整合决策可以使货拉拉链的利润大于采取不整合决策的利润;当服务创新系数较小,链间价格竞争强度较大时,货拉拉平台企业和参与的社会个人企业采取不整合决策比整合决策获得的利润更高。 图的关系图 由引理3可得出如下定理: 定理3:当对手链选择整合时,对于自身LSSC而言,整合与否取决于两条LSSC之间的竞争程度和服务创新成本系数的范围。两个参数满足于: (i)当0.25 (ii)当0.25 (iii)当k≥0.2928时,0 定理3表明,当对手链选择整合时,对于自身链上的LSI而言,是否选择与下游的LSP整合,同样会受到服务创新成本系数k和竞争程度u的影响。当服务创新成本系数较小时(0.25 证明过程见附录(备索)。 由引理4可以得出,当快狗平台企业与嘉里物流企业采取集中决策进行整合,当服务创新系数较大时,无论两条链的价格竞争强度如何,货拉拉平台企业和参与的社会个人企业采取不整合决策可以使快狗链获得更高利润。 由引理4可得出如下定理: 定理4:当对手链选择整合时,对于自身LSSC而言,整合与否取决于两条LSSC之间的竞争程度和服务创新成本系数的范围。两个参数满足于: (i)当k>0.25且0 引理3和引理4结合分析,从图5中B1、B2区域还可以看出,当服务创新成本系数处于一定范围时(0.25 由此可以得出如下推论: 推论3:当服务创新成本系数k较小(0.25 引理3和引理4结合分析,从图4中B2区域还可以看出,当服务创新成本系数处于一定范围时(0.25 推论4:当(k,u)处于某个特定范围时,在同一水平发生横向Nash竞争的两条物流服务供应链,当其中一条LSSC选择任何决策时,另一条LSSC采取相反的决策能达到双赢,不仅能提升自身的整体利润,还能促进对手LSSC整体利润的提升。 值得注意的是,两条链间竞争程度对LSSC的整合决策和利润的影响会受到服务创新成本系数的限制。定理1和定理2均表明,服务投资成本系数均是从某一阈值(0.25)开始逐渐增长的,这是由于在最优化求解时,为保证两条链的目标利润函数均能取得最优值,服务投资成本系数k需要满足一定的取值要求才能使其海塞矩阵负定。对于这一情况,可能的现实原因为:当服务创新成本系数较小时,较低的服务创新成本能带来较大的供应链效益,而此时相同成本用于服务创新的效益足以应对市场供应链之间的竞争,链的最优决策应是将资金尽可能地用于服务创新获得最大效益。所以,对于供应链决策者来讲,企业应尽可能地抓住服务创新的机会,将精力资金用于服务创新,此时对于供应链是否采取整合决策将不是首要面临的问题。 以二级物流服务供应链系统为研究对象,基于链间Nash竞争和链内成员Stackelberg博弈,运用逆向推导法和对比分析,讨论两条物流服务供应链分别采取整合决策或不整合决策下整体利润、物流服务市场单价和LSSC服务水平的大小,以LSSC整体利润为判断标准,进行LSSC整合策略分析,可得研究结论如下。 第一,无论其中一条链选择何种决策,始终存在一个最优的条件,使另一条链采取不整合能够最大化自身利润同时提升对手链的利润。从供应链角度考虑,并不是一味地对物流服务供应链采取整合决策使供应链利润最大。无论对手链采取整合或者不整合决策,均有可能自身采取不整合反而是最优决策,不仅能提升自身链利润,还能提升对手链的利润。对于自身链来说,是否采取整合决策均需要根据服务创新成本系数和链间竞争程度来决定。 第二,在服务创新成本系数较大(大于某个值的特定范围)时,在同一水平发生横向Nash竞争的两条物流服务供应链上,LSSC的整合决策只取决于服务创新成本系数的大小,与链间服务竞争程度无关。当对手链采取不整合策略时,此时与对手链采取相同的策略可以达到双赢状态;当对手链采取整合策略时,此时自身链采取整合策略使自身利润最大,但降低了对手链的利润,两条链可能会陷入囚徒困境。 第三,两条链间竞争程度对LSSC的整合决策和利润的影响会受到服务创新成本系数k的限制。当服务创新系数较小时,两条链间竞争程度对LSSC的整合决策才会有影响。在服务创新成本系数较小,对手链采取整合决策时,(1)较小竞争强度下自身链采取对手链相反策略能达到双赢状态,采取相同策略可能会陷入囚徒困境;(2)较大竞争强度下自身链采取相反策略为双赢,采取相同策略为双输即两条链均不是最优策略。在服务创新成本系数较小,对手链采取不整合决策时,(1)较小竞争强度下自身链采取相反策略达到双赢;(2)较大竞争强度下自身链采取相同策略可以达到双赢。 第四,在两条LSSC竞争过程中,LSP服务创新成本系数和链间服务竞争程度会影响到两条LSSC各自的整合决策。对手链在进行选择整合或不整合策略时,服务创新水平和链间竞争强度等指标都会引起自身链纵向整合决策的变化。从企业角度来说,其在对纵向结构进行决策时不仅要考虑自身未来的发展战略,还要结合市场的横向竞争因素,将内部因素与外部竞争合适地组合才能使企业实现利润最大化。根据不同的市场环境及时调整自己的纵向战略,合理地规避风险,才能增强企业竞争力。 本文还存在些许不足之处,首先,现实中两条LSSC之间可能存在主从博弈的可能,以及两个LSP的服务创新成本系数可能是不相等的。本文仅考虑了两条链之间权利平等,创新成本系数相等的情况。其次,本文以供应链整体利润最大为判断标准研究供应链的最优整合决策,该决策是保证了供应链整体利润最优,决策后供应链增加的利润如何分配将需要以后进一步进行研究。最后,本文只考虑两条竞争链均为一个物流服务集成商和一个物流服务提供商两级的物流服务供应链的整合决策。现实中,在面对多条供应链相互竞争时,或者竞争的两条链为一个物流服务集成商对应多个物流服务提供商时,整合决策是否均受竞争强度和服务创新系数影响?这些将是以后进一步研究的方向。
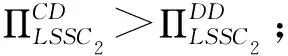
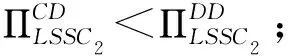
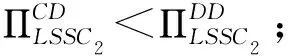
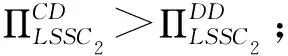
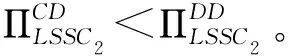
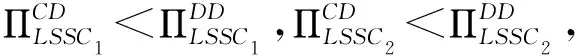
(二) 对手链选择整合(C)时,自身链的利润比较

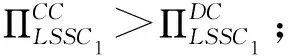
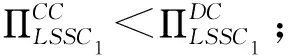
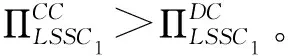



六、 结论与展望
