采用余弦相似度和变预测时域的汽车轨迹追踪控制

2022-11-25钟聪彭育辉黄炜

福州大学学报（自然科学版） 2022年6期

钟聪，彭育辉，黄炜

(福州大学机械工程及自动化学院，福建福州 350108)

0 引言

作为支撑汽车自动驾驶的关键技术之一，轨迹追踪要同时具有优异的行驶稳定性和满足追踪精度的要求.轨迹追踪的横向控制方法主要包括PID控制、滑模控制、线性二次高斯控制、模型预测控制(model predictive control，MPC)等[1-4].由于MPC能够系统地处理汽车模型存在的动力学和运动学约束问题，故被广泛地应用于自动驾驶汽车的轨迹追踪控制中.Lin等[5]设计一种MPC自适应控制器，基于线性轮胎模型在线实时估计轮胎侧偏刚度，并更新控制器预测模型，但未考虑中高速工况下轮胎的非线性特性，故在中高速工况下的追踪精度与稳定性并不理想.蔡英凤等[6-7]利用可拓集的关联函数动态分配轨迹追踪精度和横向稳定性的权重系数，建立智能车辆轨迹追踪的多目标模型预测可拓协调控制方法.Wang等[8]设计一种改进型MPC控制器，结合模糊控制来实时改变MPC的权重参数，在保证追踪精度的同时，也提高车辆的转向稳定性.Yuan等[9]设计一种车速自适应的MPC控制器，通过模糊控制和神经网络预测器获得期望航向偏差，以解决控制器在不同车速下的过早转向和转向超调问题.白国星等[10]基于非线性模型预测控制算法，设计一种可变预测时域的轨迹跟踪控制器，提高控制器对中低速工况的自适应性.Rokonuzaman等[11]以MPC控制器为基础，利用神经网络学习车辆动力学模型使用过的数据，得到被控车辆的前轮转角，在参数不确定的情况下该方法的控制性能优于传统MPC，但神经网络的参数设置问题仍有待解决.

综上，目前基于MPC的汽车轨迹追踪算法仍面临两个关键问题：一是控制策略未考虑预测模型状态矩阵变化和预测时域变化对轨迹追踪精度、车辆稳定性的影响；二是控制器对高速工况的自适应能力较差.本研究提出一种基于余弦相似度和变预测时域的轨迹追踪控制策略，能根据实际行驶工况变化对预测模型、预测时域、控制时域进行相应的在线优化，从而提高控制器对高速工况的自适应能力和轨迹追踪精度.

1 控制策略的总体思路

可在线优化MPC轨迹追踪控制方法的算法包括线性时变MPC控制器的求解和预测模型的在线优化两个模块.基于初始预测模型，根据车辆当前状态、参考位置和参考横摆角，通过线性时变MPC控制器求解出最优前轮转角；再根据车辆实时状态、纵向车速和横向车速，预测模型优化模块，计算出当前预测模型状态矩阵和初始预测模型状态矩阵的余弦相似度.如果余弦相似度低于预定阈值，就将当前的状态矩阵更新到MPC的预测模型中.同时，根据当前的纵向车速和横向车速，基于模糊控制规则对预测时域和控制时域进行相应的调整优化，以期提升控制器对高速工况的自适应能力、提高汽车轨迹追踪的精度和横摆稳定性.

2 基于MPC的轨迹追踪控制方法

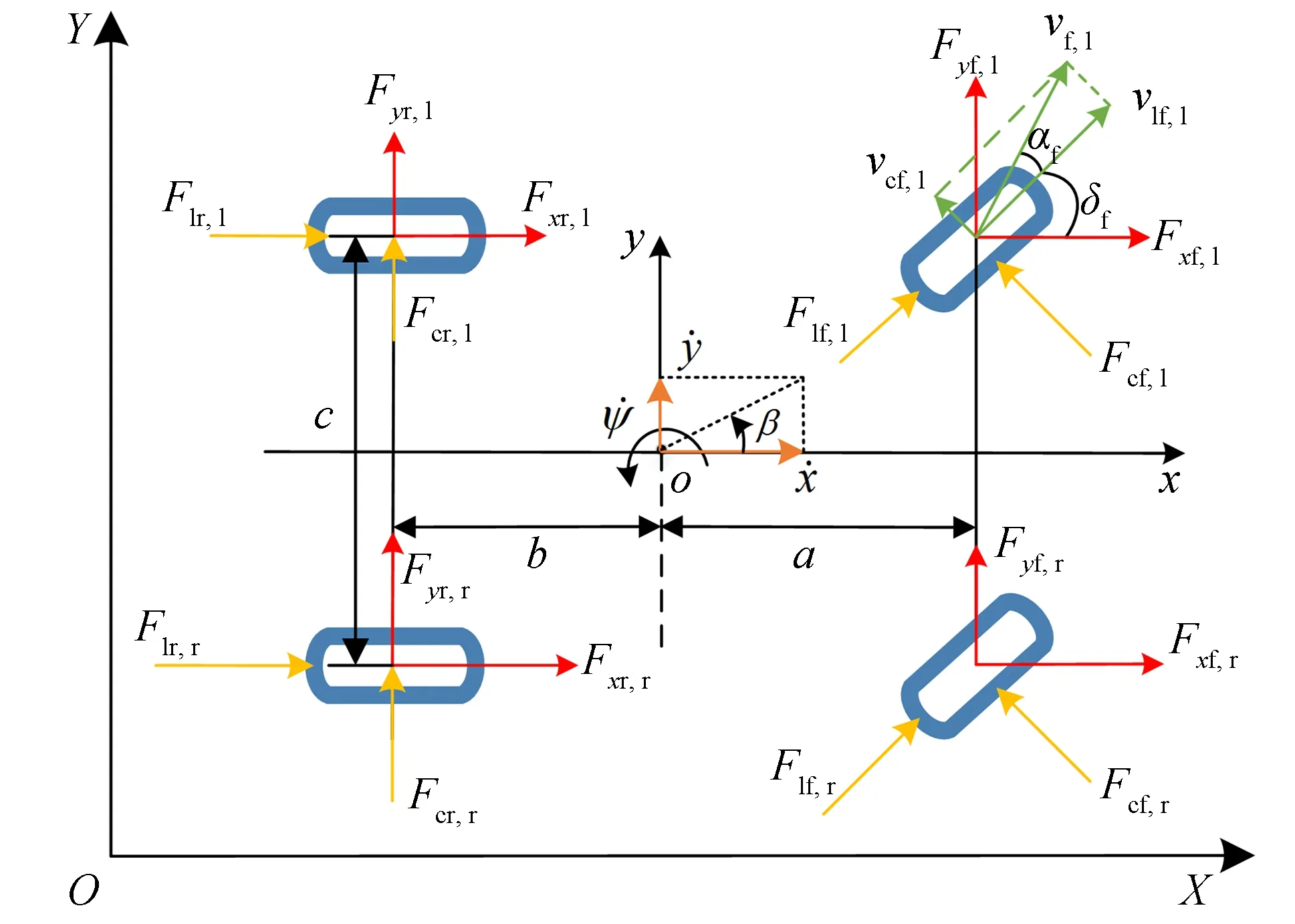
图1 车辆动力学模型Fig.1 Model of vehicle dynamics

车辆侧向运动和横摆运动的动力学微分方程[12]为：

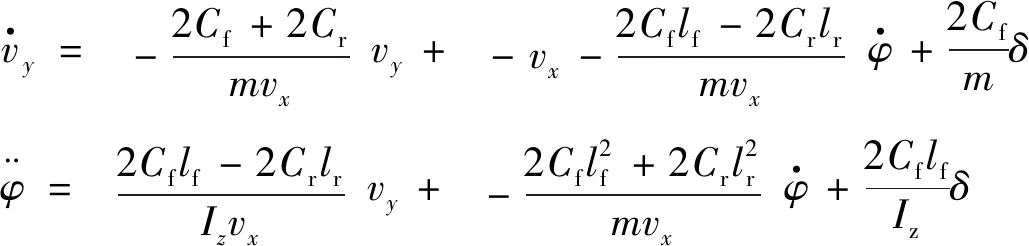
(1)

式中：m为车辆质量；Iz为车辆相对z轴的转动惯量；Cf，Cr分别为前后轮的侧偏刚度.

连续时间状态空间方程[12]为：

(2)

状态空间表达式为：

(3)

为简化车辆模型，提高MPC控制器的计算速度，假定车辆前、后轮侧偏刚度为定值，且车辆载荷不发生变化，即状态矩阵A为线性定常矩阵.离散化后的状态空间表达式[12]为：

(4)

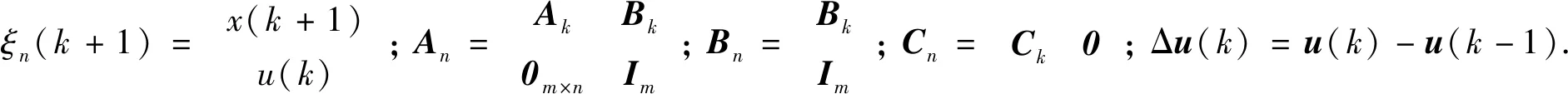
系统预测时域为Np，控制时域为Nc，系统预测时域内的输出序列可表示为：

(5)

根据公式(5)，以前轮转角增量为新的控制变量，可以得到一组新的状态空间方程：

Y0(k)=R0ξ0(k)+Z0ΔU0(k)

(6)

参考横向位置Yr和参考横摆角φr为已知量，作为参考信号输入，用来计算汽车的实时横向位置和横摆角度.轨迹追踪控制是为实现预测时域内车辆状态的预测，由价值函数J计算出控制时域内的输出序列，使车辆的实际行驶路径尽可能地贴近参考路径.即：

(7)

考虑车辆实际特性，还需对系统的状态量和控制量进行一定的约束，包括：1) 横向位置约束：ymin≤y(k)≤ymax；2) 横摆角约束：φmin≤φ(k)≤φmax；3) 控制量约束：umin≤u(k)≤umax；4) 控制增量约束：Δδmin≤Δu(k)≤Δδmax.

将价值函数(7)改写成一个标准的二次规划问题：

(8)

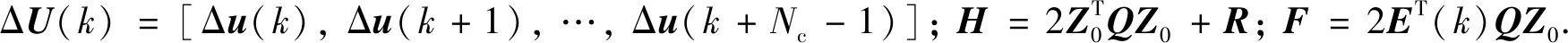
在每一个优化周期内，优化目标为求取价值函数J的最小值，得到控制时域内控制变量的增量：

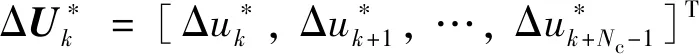
(9)

如下式所示，选取控制序列的第一个元素作为实际的控制变量(即前轮转角)作用于被控对象.

u(k)=u(k-1)+Δu*(k)

(10)

3 可在线优化的方法

3.1 采用余弦相似度的状态矩阵在线优化

上述线性时变MPC控制器的状态矩阵是基于预先设定的纵向车速来获取的.当纵向车速变化率过大或车速达到30 m·s-1时，将不能满足无人驾驶追踪精度和稳定性的要求，甚至会出现车辆失稳的现象[13].

为提高控制器对不同车速的自适应能力和模型预测的精度，要求控制器能根据汽车实际车速变化对预测模型的状态矩阵进行优化.因此，提出一种基于余弦相似度的状态矩阵在线优化策略，即用矩阵的余弦相似度来度量两个矩阵的差异程度，从而确定预测模型的优化节点，获得最符合当前车速的预测模型.两个状态矩阵A和A*的余弦相似度r为：

(11)

式中：A为用历史车速计算得到的状态矩阵；A*为根据实时车速计算得到的状态矩阵.

余弦相似度的值介于0和1之间，该值越接近1，说明矩阵A*越接近A，两个矩阵相似度越高.一旦两个状态矩阵的余弦相似度低于预设阈值，就将车辆此时的实际速度代入式(3)中，以此更新优化状态矩阵A.

3.2 预测模型的在线优化

控制器参数的选取对轨迹跟踪效果影响较大，预测时域和控制时域是其中最重要的两个参数[10].预测时域过大，控制器将会过多地考虑前方距当前位置较远处的误差，导致追踪精度下降；预测时域过小，将会导致控制量非常接近甚至超过约束值，致使汽车无法及时转向，降低车辆稳定性.若控制时域较大，在精确度没有明显提升的情况下，会增加计算量；若控制时域较小，控制器会对误差过于敏感，降低车辆稳定性.综上，车辆在横向车速较大时，控制时域应该减小，以保证车辆的行驶稳定性；在横向车速较小时，控制时域应该增大；在纵向车速较大时，为提高追踪精度，预测时域应该增大；在转弯的时候，预测时域要相应地减小.因此，预测时域和控制时域的大小应该通过实际纵向车速和横向车速共同决定.

模糊控制不需要建立精确的数学模型，且其自适应能力和鲁棒性较强.因此，根据纵向车速和横向车速，采用模糊控制方法对时域系数τ进行调节，进而调节预测时域和控制时域，以适应轨迹跟踪精度和稳定性的要求.经过Matlab仿真，最终制定的模糊规则如表1所示.获得的输入纵向车速、横向车速与输出时域系数的响应关系如图2所示.

表1 时域系数的模糊控制规则Tab.1 Fuzzy control rules of the time domain coefficients

图2 时域系数与车速的关系Fig.2 Diagram of time domain coefficient and speed

为进一步提升时域系数的自适应能力，需要充分考虑纵向车速和横向车速对预测时域和控制时域的影响.当车辆在直线道路上行驶时，横向车速vy很小，近似为0，此时预测时域和控制时域可设置大一些；当汽车转弯时，vy会随着道路曲率的增加而增加，此时转向角较大，预测时域和控制时域要相应地减小.因此，预测时域和控制时域的计算式为：

(12)

式中：T为采样时间，取0.01 s；ω为权重系数.

根据式(12)得到当前时刻t的状态空间模型和价值函数分别为：

(13)

4 仿真验证

4.1 预测模型状态矩阵在线优化的有效性验证

表2 不同阈值对余弦相似度及其变化率的影响Tab.2 Influence of different thresholds on cosine similarity and its change rate

当前状态矩阵和历史状态矩阵的余弦相似度低于优化阈值(TH)时，就对当前状态矩阵进行优化更新.为分析不同优化阈值对余弦相似度及其变化率的影响，对4组不同阈值(0.80、0.85、0.90和0.95)[14]下的状态矩阵余弦相似度及其变化率进行Matlab/Simulink仿真分析，其具体数值和仿真所得对比数据如表2所示，仿真结果对比如图3所示.由表2和图3可以看出，随着阈值的增大，状态矩阵的优化次数明显增加，相邻优化节点间的最大速度差(Δvmax)和余弦相似度的变化率呈现先增大后减小的趋势.阈值为0.90时的优化次数、Δvmax和余弦相似度的变化率都要优于阈值为0.80、0.85时的值.与阈值为0.95时相比，阈值为0.90时的Δvmax有很大提升，说明此时速度的适应范围较广.阈值为0.90和0.95时的优化次数相同，说明这两种情况下的计算量相当.如果继续增大阈值，当前状态矩阵和历史状态矩阵的余弦相似度将更难达到阈值，优化次数会相应增加，从而导致计算量的显著增加，影响控制器的实时性.综上，状态矩阵优化后的预测模型对实时变化的车速具有更强的适应能力.同时，当阈值取0.90时，预测模型既能保证较强的速度自适应性，又无需频繁更新状态矩阵，进而减小MPC控制器的计算强度.

图3 不同阈值对余弦相似度及其变化率的影响Fig.3 Influence of different thresholds on cosine similarity and its change rate

4.2 预测时域和控制时域的权重系数的确定

为合理确定权重系数，需先研究预测时域和控制时域的权重系数对轨迹追踪控制器的精度和稳定性的影响.对4组不同权重系数(0.6、0.7、0.8和0.9)[15]下的轨迹追踪精度和稳定性进行Matlab/Simulink和CarSim联合仿真分析.图4为选取的纵向速度，速度变化范围为5～30 m·s-1.图5为不同权重系数下追踪时的横向速度变化，仿真工况选取双移线工况.图6为不同权重系数下追踪时的横向位置和横摆角变化.

图4 纵向车速Fig.4 Longitudinal velocity

图5 不同权重系数下的横向速度Fig.5 Lateral velocity with different weight coefficients

图6 不同权重系数对追踪精度和稳定性的影响Fig.6 Influence of different weight coefficients on tracking accuracy and stability

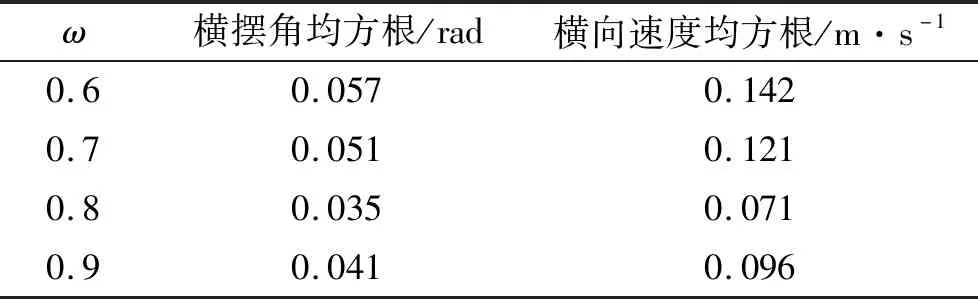
表3 横摆角均方根和横向速度均方根对比Tab.3 Root mean square of yaw angle and root mean square of transverse velocity

由图5、6和表3可以看出，随着权重系数的增大，汽车横摆角均方根和横向速度均方根先减小后增大.当ω=0.8时，汽车横摆角均方根和横向车速均方根的值都要小于其他3组值，汽车横摆角曲线和横向速度曲线的平滑度和波动都要优于其他3组曲线，说明此权重系数下的车辆稳定性较好.进一步分析图5可知，当ω=0.8时，横向速度能适应道路曲率的变化，说明此权重系数下的车辆稳定性较好，对道路弯道的敏感性较强，车辆横向车速能随着弯道的增大而增大.在大转角工况下，即横向车速处于相对较高的区域，控制时域不会过小，可保证车辆在轨迹追踪时的稳定性.因此，ω取0.8较为合适.

4.3 控制器整体的有效性验证

在Matlab/Simulink和CarSim联合仿真平台中，选取双移线工况和图4所示的纵向速度，验证所构建的可在线优化MPC控制器对不同车速和不同道路曲率的自适应能力.

图7、8分别显示轨迹追踪结果和状态矩阵在线优化的节点.如图7所示，在第一弯道和第二弯道处，可在线优化MPC控制器的追踪精度和平稳性都要优于线性时变MPC控制器.如图8所示，在第三弯道之前，可在线优化MPC控制器预测模型的状态矩阵进行5次优化，每次优化都会使得当前的预测模型更加匹配实际车速，从而提高轨迹追踪的精度和稳定性.在第三弯道处，实际车速已达30 m·s-1.由于线性时变MPC控制器没有进行模型优化，故预测模型不能很好匹配当前高速工况，导致轨迹追踪失败，车辆失去稳定性；而可在线优化MPC控制器在第三弯道前进行预测模型优化，使得整个预测模型与实际高速工况有很高的匹配度，因此在第三弯道处仍有较好的轨迹追踪能力.利用平均绝对百分比误差对横向位置和横摆角进行评价对比，可在线优化MPC控制器比线性时变MPC控制器的追踪精度和横摆稳定性分别提高29.45%和18.19%.仿真结果表明：与线性时变MPC控制器相比，所提出的可在线优化MPC控制器在不同车速下的轨迹追踪精度和车辆稳定性均有明显的提升.

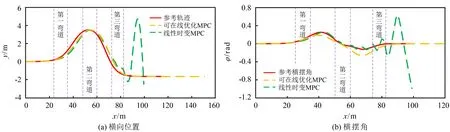
图7 轨迹追踪结果Fig.7 Trajectory tracking results

图9表示轨迹追踪过程中的车辆横向速度变化；图10表示轨迹追踪时，预测时域和控制时域随纵向、横向车速变化响应图.由图9和图10可知，在第一弯道处，随着纵向车速的下降和横向车速的变化，可在线优化MPC控制器的预测时域和控制时域都能相应的减小，提高轨迹追踪精度和稳定性.在第二弯道处，随着纵向车速的增加和横向车速的正向增加，预测时域和控制时域也相应的增大.同时，控制时域的增长幅度相比于预测时域要低，可避免因控制时域过大而引起计算量增加.在第三弯道处，车辆横向车速达到负向最大，说明车辆正处于大弯道区域.此时，预测时域和控制时域都需要相应减小，使可在线优化MPC控制器能够在短时间内求解出最稳定的前轮转角，确保车辆在稳定的前提下能够以较高的精度通过第三弯道.显然，基于模糊规则的预测时域和控制时域控制方法能较好地适应纵向、横向车速的变化.