Allee效应对Lotka-Volterra捕食-食饵模型的动力学行为影响
2022-11-25周起梅林思佳陈凤德陈晓英
周起梅,林思佳,陈凤德,陈晓英
(1.福州大学数学与统计学院,福建 福州 350108;2.福州大学至诚学院,福建 福州 350002)
0 引言
近年来,研究具有Allee效应的生态种群模型的动力学行为已经成为生物数学研究领域的一个核心研究方向.许多学者对具有Allee效应的捕食者-食饵模型进行了稳定性分析[1-7].文献[3]提出了以下食饵具有Allee效应的Lotka-Volterra捕食-食饵模型:

(1)
其中:β是一个正常数,用来描述Allee效应的强度.文献[3]证明了具有Allee效应的系统需要较长的时间才能达到稳态解,Allee效应降低了捕食者和食饵种群在稳态下的种群密度.
最近,文献[8]中提出了一类Lotka-Volterra捕食-食饵的离散模型:

(2)
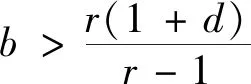
众所周知,对于生命长、世代重叠并且数量很多的种群,常常可近似地用连续模型来刻画.食饵具有Allee效应究竟会对连续的Lotka-Volterra捕食-食饵系统产生怎样的影响呢?受文献[1]启发,本研究提出如下模型:
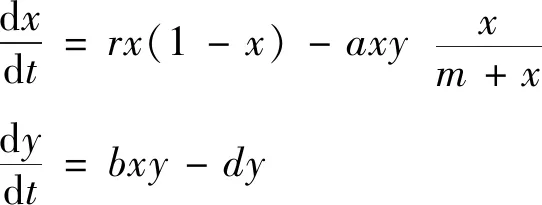
(3)
1 平衡点的存在性
无论系统(3)的参数如何变化,该系统总存在两个边界平衡点E0(0,0)和E1(1,0),接下来讨论系统(3)正平衡点的存在情况.
定理1Ⅰ) 当b≤d时,系统(3)无其他平衡点;
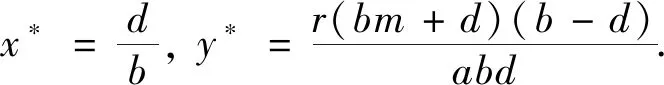
证明 系统(3)的平衡点由下面系统给出:

(4)
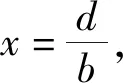

2 平衡点的稳定性
系统(3)的雅可比矩阵计算如下:
定理2Ⅰ) 边界平衡点E0(0,0)总是不稳定的且为鞍点;
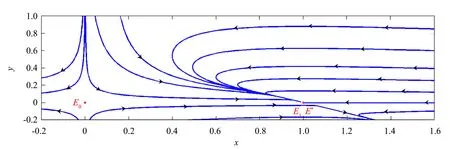
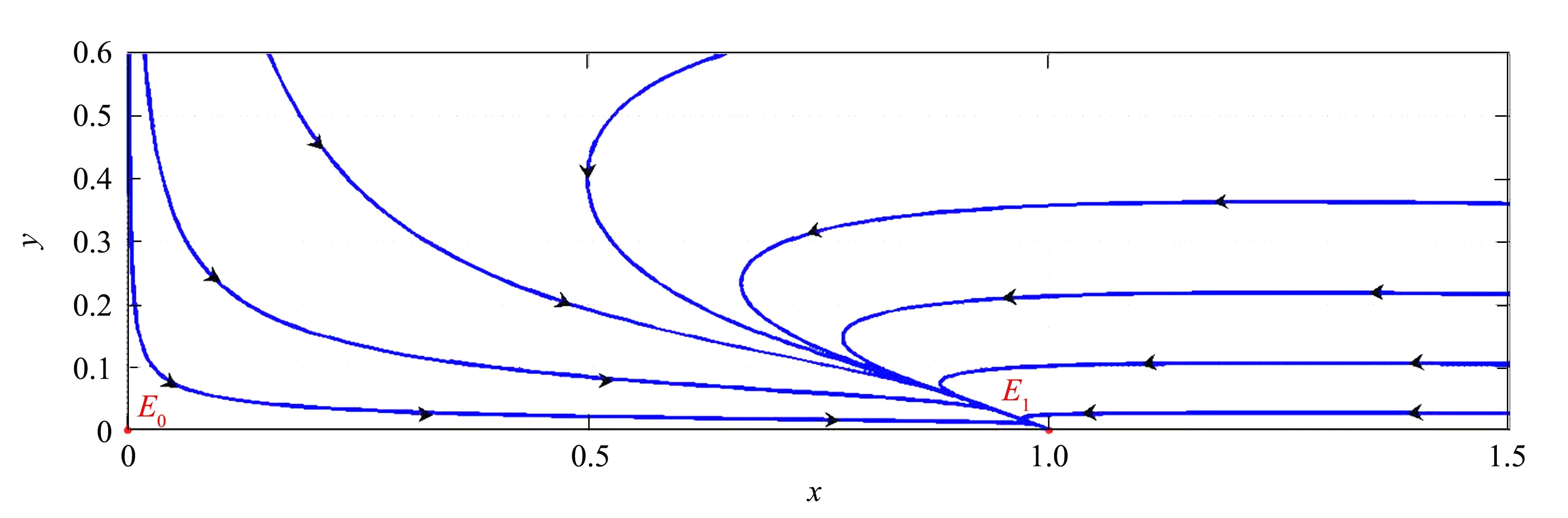
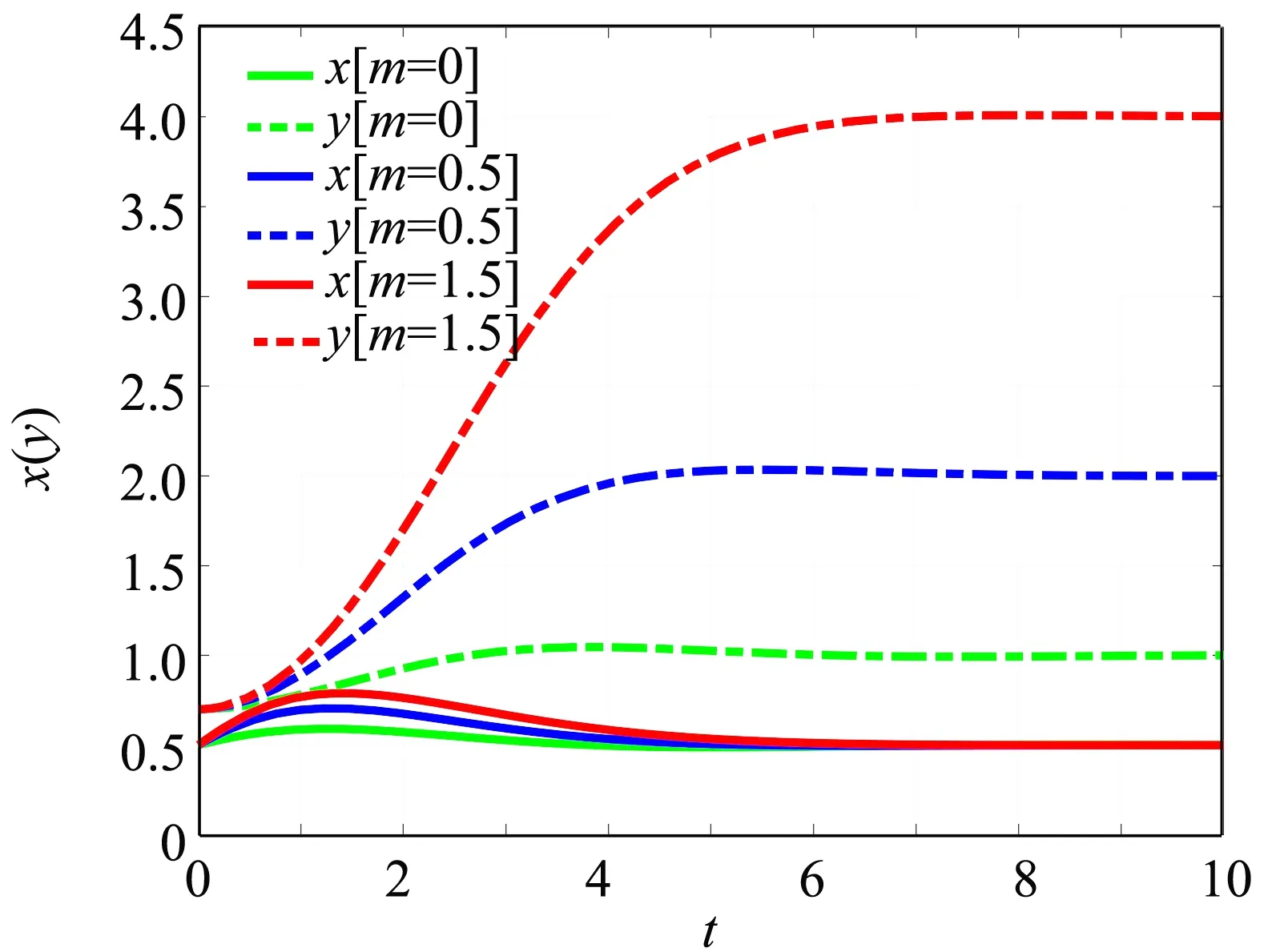
Ⅱ) 关于边界平衡点E1(1,0),有以下结论:(a) 若b>d时,E1(1,0)是不稳定的且为鞍点;(b) 若b 证明 系统(3)在E0(0,0)处的雅可比矩阵为: 其特征值分别为:λ1=r>0,λ2=-d<0.因此,边界平衡点E0(0,0)总是不稳定的且为鞍点.系统(3)在E1(1,0)处的雅可比矩阵为: (5) 其中:P1(X,Y)和Q1(X,Y)是XiYj(i+j≥3)在点O(0,0)附近的解析函数. 由隐函数定理可得:存在唯一的隐函数X=φ(Y)使得φ(0)=0和P(φ(Y),Y)=0.由式(5)的第一个方程可得: (6) 把式(6)代入式(5)的第二个方程可得: (7) 定理4当b 证明 由定理1和定理2知,当b (8) 注1:文献[1]证明了差分系统(1)随着系统参数的变化存在Neimark-Sacker分岔.本研究表明,对连续系统而言如果系统正平衡点存在,则必是全局渐近稳定的,因此不可能有分支现象. 分别用例1~2来说明主要结果的可行性. 例1考虑如下系统: 相对于系统(3),取定参数r=2,d=1,a=5,m=0.5. 1) 若取定b=4,由定理1、2和5知,存在两个边界平衡点E0(0,0)、E1(1,0)和唯一正平衡点E*(0.25,0.9),且有E0(0,0)和E1(1,0)为鞍点,唯一正平衡点E*(0.25,0.9)是全局渐近稳定的(见图1). 图1 系统(3)的数值相位图Fig.1 Numerical phase portraits of system(3) 2) 若取定b=1,此时E*(x*,y*)与E1(1,0)重合.由定理1~2知,仅存在边界平衡点E0(0,0)和E1(1,0),其中E0(0,0)为鞍点,E1(1,0)为结点(见图2). 图2 E0,E1,E*的相图Fig.2 Phase diagram of E0,E1,E* 3) 若取定b=0.8,由定理5知,边界平衡点E1(1,0)是全局渐近稳定的(见图3). 图3 E0,E1的相图Fig.3 Phasediagram of E0,E1 例2考虑如下系统: 相对于系统(3),取定参数(r,d,a,b)=(2,1,1,2). ① 取系统初值(x0,y0)=(0.5,0.7),绿蓝红分别表示m为0、0.5、1.5(见图4).由图4可知,随着Allee效应的增加,捕食者种群达到的稳态解也随之变大,即捕食者种群的最终平衡密度也随之增加.但无论Allee常数m如何变化,始终不影响食饵的最终平衡密度.另一方面,图4说明在初值相同的情况下,受Allee效应影响的连续Lotka-Volterra捕食-食饵系统需要更长的时间才能达到稳态解.值得注意的是,随着m的增大,需要更长的时间才能达到稳态解. ② 取m=0.5,此时唯一正平衡点E*(0.5,2.0)全局渐近稳定(见图5). 图4 Allee效应对E*趋于平衡的速度影响Fig.4 Effect of Allee effect on the rate of E* tending to equilibrium 图5 种群初始密度对E*趋于平衡的速度影响Fig.5 Effect of the initial population density on the rate of E* tending to equilibrium 绿红蓝分别表示系统初值为(x0,y0)=(0.4,1.2),(x0,y0)=(0.5,2.0)和(x0,y0)=(1.2,2.5).图5说明种群的初始密度始终不会影响种群的最终平衡密度,若种群初始密度并非最终平衡密度,则初始密度对系统达到稳态解所需要的时间不产生影响. 本研究分析了食饵具有Allee效应的Lotka-Volterra捕食-食饵模型,通过数值模拟研究Allee效应对种群密度的影响.一方面,与系统(2)相比,证明了参数b和d对系统的稳定性有很强的影响;另一方面,得到了与Merdan等学者相同的结论,即在种群初始密度相同的情况下,受Allee效应影响的连续Lotka-Volterra捕食-食饵系统需要更长的时间才能达到的稳态解.然而,与Merdan等学者研究的连续系统相比,不仅分析了种群的初始密度对系统达到稳态解所需要的时间,以及种群的最终平衡密度的影响.而且发现了随着Allee效应的增加,捕食者种群的最终平衡密度也会随之增加,这就使得捕食者种群灭绝的可能性降低,有利于维持生态平衡.
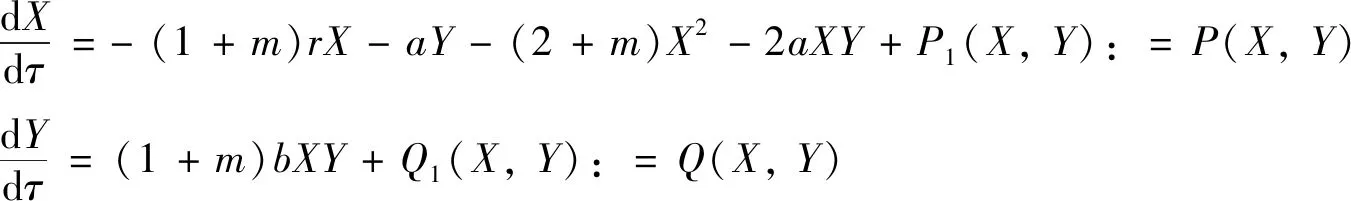
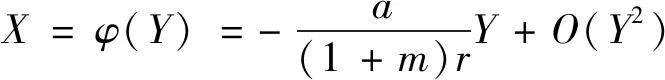




3 全局渐近稳定性


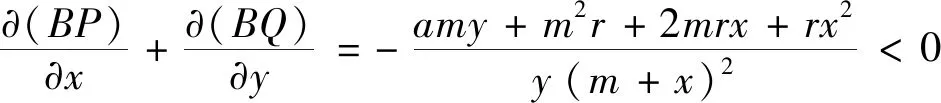
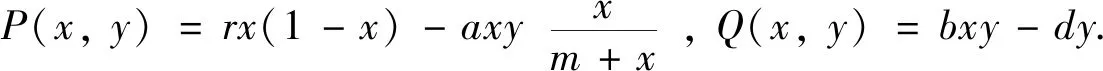

4 数值模拟
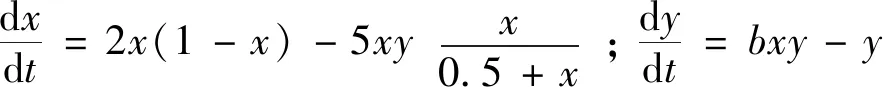


5 结论
