基于轻量化深度卷积神经网络的电机轴承故障诊断

2022-11-25殷海双牛智楷

组合机床与自动化加工技术 2022年11期

殷海双，牛智楷

(东北石油大学电气信息工程学院，大庆 163318)

0 引言

电机作为复杂电气设备之一，逐渐向大规模和智能化的方向发展。其中，滚动轴承作为机械设备的关键零部件之一,工作是否可靠将直接影响设备的正常运行[1]。其一旦发生故障，会导致整个工作过程出现问题，影响机械效率。因此对电机的运行状态进行监测和诊断在过程自动化方面具有重要意义[2]。

目前，电机轴承故障诊断方法有传统诊断方法和深度学习两种。传统的基于数学模型的电机轴承故障诊断技术已经十分成熟。LI等[3]采用了不同尺度的小波系数进行小波分解，并用最小二乘支持向量机对电机轴承故障进行诊断。BERREDJEM等[4]采用了模糊专家系统对电机轴承进行故障诊断，采用相似度分离方法从数值数据中自动归纳出模糊规则。但是传统的故障诊断方法过于依赖专业技术人员通过大量专业知识进行判断。现在机械运转中不可测因素的较多，传统的故障诊断就存在了一定的局限性[5]。

HINTON等[6]提出了深度学习的思想，证明了深度学习不需要依靠过多的人工经验。QIN等[7]提出了一种基于一维卷积神经网络的轴承故障诊断方法，通过不断调整超参数得到了一个较好的模型，最后通过实验证明了识别准确率达到99%。JIAN等[8]提出一种一维融合神经网络，它结合了自适应一维卷积神经网路与宽核和(D-S)证据理论，通过实验证明了能有效提高模型的跨域自适应能力。JANSSENS等[9]为了减少特征工程的开销，提出了一种基于卷积神经网络的状态检测特征学习模型，对多个轴承进行了测试，确保了模型的泛化性。上述方法只基于一维的轴承故障信号，没有有效利用信号的富含的大量信息。

针对深度学习在轴承故障诊断为了获得更好诊断效果不可避免的增加网络的深度，从而导致网络参数量大，占用太多设备内存的问题，提出了一种轻量化深度卷积神经网络的轴承故障诊断方法[10]。首先，搭建了深层卷积神经网络；引入残差结构提高模型的检测精度；并融合深度可分离卷积(depth separable convolution)减少模型的参数量，提升模型泛化性。

1 基本理论。

1.1 卷积神经网络

卷积神经网络(CNN)主要由输入层、卷积层、池化层、全连接层以及输出层组成，通过搭建合理的网络结构以及参数组合，原始样本数据通过在CNN网络中卷积层和池化层之间的交替迭代，以实现对样本数据的特征提取和学习。卷积层利用卷积核对上一层的特征激活图进行卷积运算，再将运算结果代入激活函数得到卷积层的输出，第l个卷积核的输出可表示为：

(1)

式中，K为特征图的总个数；f()为激活函数；W为卷积核；b为偏置量。

普通卷积的参数量大小计算公式为：

C=Z*Z*K*N

(2)

式中，Z为卷积核的大小；K为输入的特征图数量；N为输出的特征图数量。

卷积的运算图示如图1所示。

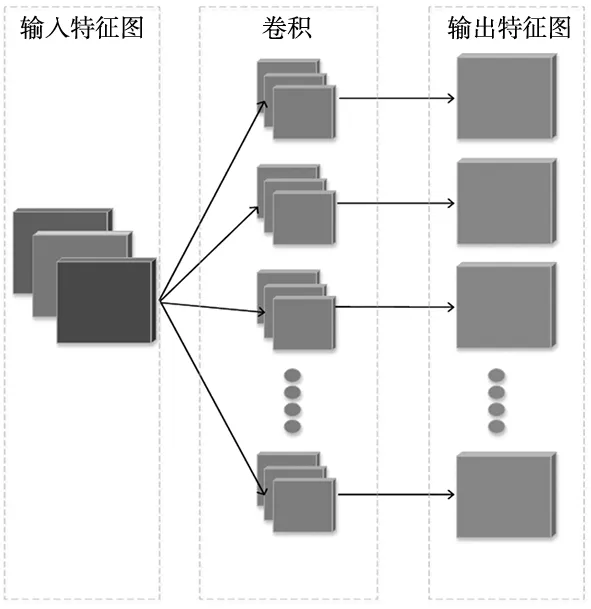
图1 卷积

1.2 池化

池化层一般是对特征图进行下采样，降低特征图的大小，浓缩特征图的特征。池化操作主要分为平均池化和最大池化，它们不参与网络的学习，因此不会有额外的参数。但是池化可能造成信息丢失，因此本文采用卷积操作代替池化进行降采样，但使用全局平均池化代替全连接层大量减少网络参数。平均池化的计算表达式为：

(3)

式中，i,j分别为池化区域的行列数；xi,j为每个位置对应的特征值。

1.3 时频转换

电机轴承振动信号属于非平稳信号，采用时域分析无法清除的看到其频率特征，而采用频域分析又无法观测到其频率随时间的变换过程。因此本文选用时频分析。时频分析中短时傅里叶变换(STFT)比较依赖与人为选择窗函数的大小，并且其无法对时域和频域的分辨率同时兼顾，对于非平稳信号而言，需要时频窗口具有可调性。连续小波变换(CWT)引入了窗函数，并定义了变换，因此兼顾了时域和频域特性。连续小波变换的变换表达式为：

(4)

式中，a为控制小波变换的中心频率；b为位移系数，控制小波基在时间轴上沿着信号滑动；φa,b(t)为小波函数基，它是由同一母函数φ(t)经伸缩和平移后得到的一组函数序列。

由上可知，连续小波变换通过不同尺度变换的小波基函数能准确刻画信号的时域特征。本文选择的小波基函数为cmor3-3。如图2所示为一组轴承振动数据的时域图和其对应的时频图。时频图中横坐标由8个刻度，纵坐标范围为0～6000 Hz，用颜色表示振动信号的幅值。

图2 一维时序信号转换为二维时频信号

2 轻量化深度卷积神经网络建立

2.1 残差结构

深度学习表明随着网络深度的增加，网络越能学习到数据的深层信息，具有更好的表征能力。但实际上随着网络深度的增加模型将变的越来越难以学习甚至出现退化。本文采用残差结构[11]改善这种现象，如图3所示。残差结构的提出使得网络变的更加容易训练，在深层卷积神经网络中仍然可以得到不错的效果而不会出现退化，使得深度学习模型可以搭建的更深。图中3a为刚开始提出的残差结构，称为残差结构1，之后作者又在文献[12]中证明了前激活的时候残差结构更容易反向学习，信息更不容易丢失，因此出现了图3b，称为残差结构2。本文采用残差结构2改进网络结构，提升网络性能。

图3 残差结构

图3中，x为输入的数据，其中f(x)是经过网络学习之后输出的特征。残差结构期望网络的输出g(x)=f(x)+x，从而网络学习的特征由原来的g(x)变成f(x)，这样保证了当网络无法收敛进行反向传播时，可以通过残差结构的快捷路径进行传播，而正向传播时每一层可以得到浅层特征和深层特征的结合。这样有效解决了网络过深时梯度难以收敛，网络难以训练的问题，并提高了网络精度。

残差结构反向传播的表达式为：

(5)

2.2 深度可分离卷积

随着网络深度的增加，网络的表征能力将变的更好，但随之而来的问题是模型参数量的增加。模型参数量增加使得模型更大，对电脑的内存需求大，在小内存设备上无法运行。深度可分离卷积[13]的提出显著减少了模型的参数量，同时一定程度上增加了模型的泛化性。深度可分离卷积的主要结构如图4所示。

图4 深度可分离卷积

图中深度可分离卷积将普通卷积操作拆分成两步。第一部分如图4a所示为逐通道卷积。逐通道卷积对输入特征的每个通道进行独立卷积学习其每个通道的单独特征，但没有实现特征在空间维度上的融合忽略了其空间维度上的特征。逐通道卷积的参数量计算公式为：

D=Z*Z*K

(6)

式中，Z为逐通道卷积核的尺寸大小；K为输入的特征图数量。

第二部分如图4b所示为逐点卷积。逐点卷积采用1*1的卷积操作对逐通道卷积输出的特征图进行常规卷积操作，对其空间维度进行组合，在通道维度上进行加权组合输出新的单个特征图。通过这两步卷积可以将任何1*1以上的卷积进行拆分。逐点卷积的参数量计算公式为：

P=1*1*K*N

(7)

式中，K为输入的特征图数量；N为输出的特征图数量。

对深度可分离卷积和常规卷积参数量进行比较得：

(8)

可以看出，随着输出特征图的大小增加和卷积核尺寸的增加，深度可分离卷积所减少的参数越少。

2.3 网络结构

本文采用残差结构和深度可分离卷积搭建模型的单个模块，结构如图5所示。

图5 模型单个模块

本文模型总共包括10个图5模块，一个最大平均池化层，共相当于20层普通卷积。详细参数和网络结构如表1所示。

表1 模型结构

2.4 整体流程

本文提出的轻量化深度卷积神经网络对轴承的故障诊断流程如图6所示。首先对采集到的振动信号进行分类、整理。之后，使用连续小波变换将一维振动信号转化为二维时频信号，并分为训练集和测试集。然后，将训练集送入搭建好的卷积神经网络中对模型进行训练，观察模型训练时的损失值，当损失值收敛后停止训练。然后将测试集送入网络，根据指标评价网络的性能。

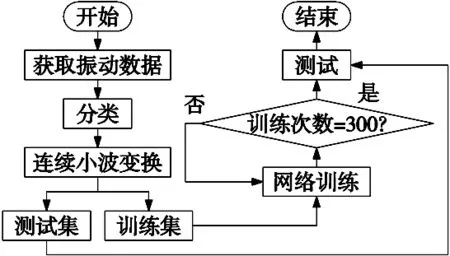
图6 整体流程图

3 实验分析

3.1 数据集制作

本文数据来源为某大学的公开轴承故障数据。选用驱动端的故障数据验证所提方法的有效性。故障点采用电火花加工，SKF轴承用来检测故障直径为0.007 in，0.014 in，0.021 in的缺陷点，NTN轴承用来检测故障直径是0.028 in的缺陷点，采样频率为12 Hz。因为轴承外圈是静止的，因此故障点相对于轴承的负载区位置将会直接影响轴承系统的振动响应。为了量化这种响应，对轴承外圈又分别在3点钟，6点钟，12点钟进行了故障点加工。现在大多数轴承故障诊断方法一般是对4类(正常，内圈故障，滚动体故障，外圈故障)，或者10类(正常，3中不同故障尺寸的外圈轴承故障、滚动体故障、内圈故障)进行诊断。为了更加贴合工程的实用性，充分利用已有的轴承数据。本文对16类轴承故障进行诊断，故障类型及编码如表2所示。表中的0.007，0.014，0.021，0.028为故障直径，单位英寸(in)。6，3，12为外圈故障点相对于轴承负载区的位置。

表2 轴承故障类型及编码

通过连续小波变换后，得到的总样本数量为8359张。各种类别样本数量如表3所示。

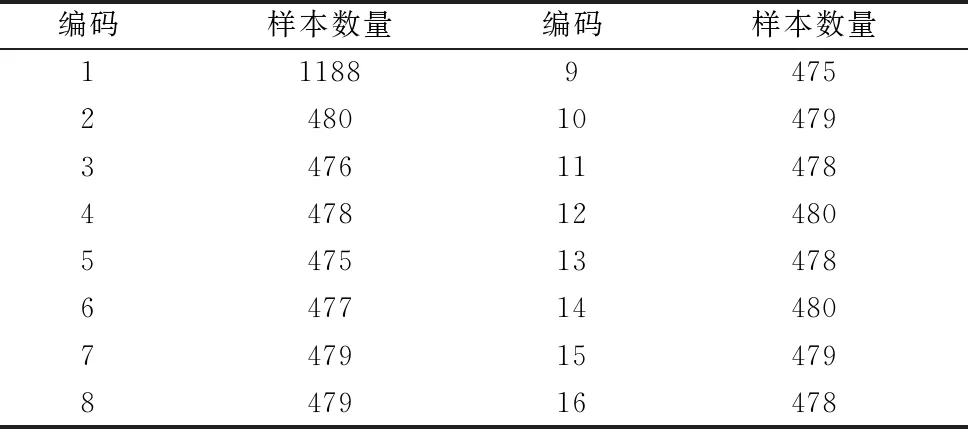
表3 各类别样本数量

3.2 参数设置

本文模型训练时的参数设置如下：输入图片大小为256*256的分辨率图像，训练采用adam优化器更新权值，学习率设置为0.001，batch为16，最大迭代次数设置为300。训练方式为GPU，采用了配置为NVIDIA GeForce GTX 1650，4 G内存的计算机。总的图片数量为8359张，按8：2分为训练集和测试集分别为6694张和1665张。

3.3 不同模型比较

为了验证本文算法的有效性和优越性，使用两种经典的深度学习模型在电机轴承故障数据集上进行训练和测试并比较了识别精确度和模型大小，分别为LeNet5和AlexNet，并且比较了残差结构1和本文所用(残差结构2)。选择训练效果最好的权重作比较。具体训练结果如图7所示。

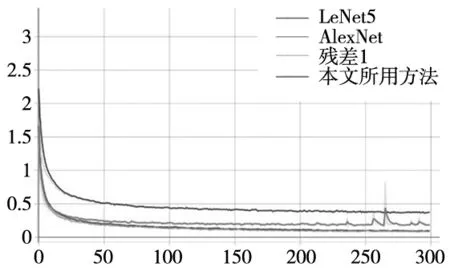
图7 损失值变化曲线

可以看出4种方法损失值都在迭代50次左右开始收敛，本文所用方法和使用残差结构1的模型明显优于LeNet5和AlexNet，损失值在更小处收敛。而本文所用方法和使用ResNet1的模型收敛值基本相等，无明显差异。为了进一步比较模型的使用性能，比较了4个模型在测试集上的准确率和模型大小。详细信息如表4所示。

表4 不同模型比较

从表4中可以看到， LeNet5和AlexNet精确度分别为0.909和0.982，使用残差结构1所得的精确度为0.994，本文所提出的方法准确率为0.997，识别精确度明显优于另外3个模型。另外本文所提模型大小只有6.23 MB，而AlexNet模型大小为60 MB，大量减少了模型大小，提高了模型的适用性。

综上所述，本文所提的方法，模型大小仅有6.23 MB，对设备内存的需求大大减小。在训练过程中损失值收敛在更小值，表明模型性能良好。在测试集中精确度为0.997，证明了其模型表现性能优于其他3种模型，具有较高的工程实用价值。

3.4 消融实验

为进一步证明本文所提的每个方法的实用性和有效性。本文对所提方法做了消融实验，分别比较不使用ResNet2和深度可分离的模型，和只使用ResNet2的模型，以及最终模型的精确度和模型大小，来验证每个方法的有效性。详细参数如表5所示，表中的√表示使用了该方法。从中可以看出本文所搭建的基本模型精确度为0.985，模型大小为46.5 MB；使用ResNet2后精确度提高了0.011，模型大小增加了0.7 MB；再添加深度可分离模块后模型精确度提高了0.001，而模型大小减少了40.97 MB。