基于PD型迭代学习的机械臂轨迹跟踪控制*
2022-11-25孟琪迪南新元张永兴
孟琪迪,南新元,张永兴
(新疆大学电气工程学院,乌鲁木齐 830047)
0 引言
在现代工业生产中,机械臂被越来越多的应用于各种加工场景。机械臂作为典型的非线性、强耦合性的复杂系统,对其控制存在一定难度。迭代学习控制属于智能控制的范畴,适用于机械臂这类重复运动的控制系统[1-2]。
迭代学习控制对有限区间内重复运动系统具有优良的控制特性,近年来应用场景不断拓展。如仿生机器鱼的轨迹跟踪控制、外骨骼机器人控制和康复机器人控制等[3-4]。在生产场景中,若机械臂的初始位置与期望输出的起始位置存在偏差,则会导致迭代学习算法收敛速度变缓,跟踪性能降低,甚至导致系统发散不稳定[5]。为解决系统存在初始位置误差的问题,严求真等[6]提出基于滤波误差初始修正的自适应迭代学习控制方法,利用修正滤波误差信号设计控制器。XU等[7]提出一种新颖的参数迭代学习控制算法,叠加一种新型惩罚函数,能实现位置、速度跟踪误差在迭代域内收敛到任意小正数。管海娃[8]在迭代学习控制中引入初始修正吸引子的概念,构造一个含有初始修正项的误差变量。达到在了机械臂在迭代区间内完全跟踪的目标。迭代学习算法的收敛性主要表现在相邻迭代之间,而在每个迭代周期内算法收敛较慢。为了解决迭代周期内算法收敛慢的问题,CHEMS等[9]将迭代学习控制与PD控制组合在一起,在每个迭代周期内加入PD控制,改善了每个迭代周期内误差的收敛速度。秦霞等[10]利用误差信息设计了机器人内置控制器的模糊PD型输入迭代学习算法,将控制信息更新到期望输入轨迹中达到改善跟踪精度的目的。另有文献设计出可变增益PD型迭代学习控制律,在迭代周期内实时修改误差信息的增益系数以减小修正时间,达到提高算法收敛速度的目的[11-12]。
以上文献只对迭代学习算法的初值条件或迭代域的收敛速度进行分析,这两个条件同时满足才能使机械臂达到良好的控制效果。部分文献只讨论了理想环境下的控制效果,应在加入扰动的情况下,检验算法的鲁棒性。本文基于滑模控制能使任意初态下的被控对象在有限时间内收敛到滑模面的特点[13],将滑模控制与迭代学习控制相融合。并利用MATLAB仿真软件证实了该控制方法的有效性和可行性。
1 机械臂动力学建模及控制描述
1.1 机械臂动力学建模
一种机械臂物理结构如图1所示。

图1 双关节机械臂系统模型
本文采用拉格朗日法对机械臂进行动力学建模,拉格朗日法属于分析力学的内容,它从功和能量的角度入手、引入了广义坐标的概念,不依赖于空间坐标系,不需要分析系统内部的约束力,适应性很强。拉格朗日法函数L定义为系统的动能K与势能P之差:
L=K-P
(1)
则体现系统的动力学状态,拉格朗日方程为:
(2)

以图1机械臂系统模型为例,使用拉格朗日法对其进行动力学建模,整理得:

(3)
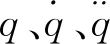
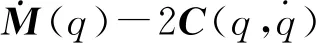
对于图1机械臂建立的动力学方程,式(3)中对应的各矩阵可写为:
(4)
式中,a=l1lc2cosq2;I=I1+I2。
(5)
式中,b=-m2l1lc2sinq2。
G=[G1;G2]
(6)
式中,
G1=(m1lc1+m2l1)gcosq1+m2lc2cos(q1+q2),G2=m2lc2gcos(q1+q2)。f=[f1;f2]
(7)
1.2 控制问题描述

系统位置跟踪误差定义为:
e(t)=qd(t)-q(t)
(8)
对不含初态误差的机械臂采用迭代学习控制时(e(0)=0),则期望能在较少次迭代次数后实现对期望轨迹的精确跟踪。对存在初态误差的机械臂系统每次迭代运行时(e(0)≠0),为了克服迭代学习控制初态误差的问题,设计复合控制律,经过有限次迭代后,跟踪误差能在迭代域[0,δ]内收敛到极小值,则机械臂系统可以在迭代域[δ,T]内实现对期望轨迹的完全跟踪(0<δ 基于滑模控制能使任意初态下的被控对象在有限时间内收敛到滑模面的特点,将滑模控制与迭代学习控制相结合,以改善迭代学习控制对存在初态误差的机械臂系统控制性能不佳和在迭代域收敛速度慢的问题。 滑模控制的设计主要包括滑模面的选择和趋近律的设计,本文选择的滑模面为: (9) 本文使用的趋近律为: (10) ARIMOTO等[2]首先设计了线性时变连续系统的D型迭代学习控制律: (11) 迭代学习控制普适性的一般形式为PID型闭环迭代学习控制律: (12) 本文选用PD型迭代学习控制律: (13) 式中,Kp、Ki、Kd为增益矩阵,通常为固定增益矩阵,也可以为时变增益矩阵。 对于机械臂系统,本文设计了将PD型迭代学习控制与滑模控制相融合的控制律,首先对式(8)、式(9)进行求导得: (14) (15) (16) 将式(3)、式(10)、式(16)合并得: (17) 融合后PD型滑模迭代算法的控制律为: (18) uk+1(t)=uk+Γ (19) 构造正定李雅普诺夫函数: (20) 对式(20)进行求导得: 把式(3),式(15)~式(17)带入上式中得: (21) 则式(20)随时间t单调递减。 (22) 令t=T,则上式为: (23) 即VK-1(t)=VK(0), (24) ΔVK(T)≤0,则表示李雅普诺夫函数VK(T)是随迭代次数递减的。 对ΔVK(T)进行累加求和得: (25) (26) 根据以上证明可知,本文设计的控制律能克服机械臂迭代初始位置与跟踪轨迹起点不一致的问题,并且加快了迭代域的收敛速度,能在更少的迭代次数下实现对期望轨迹的精准跟踪。图2为机械臂控制结构框图。 图2 机械臂控制系统结构图 为验证本文控制算法的可行性和有效性,在MATLAB/Simulink软件中对图1所示的机械臂模型进行仿真验证,机械臂各参数取值如表1所示[15]。 表1 双关节机械臂参数 两关节的位置指令分别为q1d=0.5[sin(4t)+cos(2t)]和q2d=cos(4t)+cos(3t)。每个迭代周期设定为T=5 s。 仿真试验选用PD型迭代学习控制和PD型迭代滑模控制两种算法对双关节机械臂进行轨迹跟踪控制,分别在无初态误差和含初态误差的两种初始条件下进行仿真,并加入外部干扰验证算法的鲁棒性。 在无初态误差的情况下,保持机械臂的初始状态和期望轨迹的初值一致,根据机械臂的期望轨迹曲线,得出机械臂模型的初始状态为x(0)=[0.5 2 2 0]T。使用文献[16]中PD型迭代学习控制(PDILC)和本文中提出的PD型迭代滑模控制(本文方法)两种控制方法对机械臂进行轨迹跟踪控制,分析控制性能,对比控制效果。PD型迭代滑模控制算法中各参数取值为Kp=[100,0;100,0]、Kd=[200,0:100,0]、c=[15;15]、ε=0.8、k=200。外部干扰取f=[0.3sint;0.3(1-e-t)]T。迭代域设置为5 s,迭代次数设置为10次,仿真试验结果如图3~图6所示。 图3 机械臂第1次迭代位置跟踪曲线图 图4 机械臂第10次迭代位置跟踪曲线图 图5 机械臂第1次迭代位置跟踪误差曲线图 图6 机械臂10次迭代位置跟踪误差收敛图 通过图4可以看出,PD型迭代学习控制和PD型迭代滑模控制两种控制算法经过10次迭代后,都能实现机械臂对期望轨迹的精确跟踪,但图3~图5表明,PD型迭代学习控制在首次迭代时对机械臂的控制性能欠佳,存在较大的位置跟踪误差。而PD型迭代滑模控制方法能实现在首次迭代时实现机械臂对期望轨迹的精确跟踪。由图5~图6可知,PD型迭代学习控制算法的收敛性表现在每两次迭代之间,在每次迭代过程中,其算法收敛性较差。本文设计的PD型迭代滑模控制算法在每次迭代过程中引入滑模控制,改善了PD型迭代学习控制算法在迭代域误差收敛性差的问题。 在实际工作场景中,很难保证机械臂的初始位置与期望轨迹的起点重合,通常机械臂的起始位置会位于期望轨迹起点一个很小的邻域内。假设机械臂的初始位置随机分布于与期望轨迹起点位置误差最大绝对值为0.2 rad的邻域内[17],取误差最大的位置做仿真分析,则设定机械臂初始位置为x(0)=[0.3 2 1.8 0]T,其他仿真参数与无初态误差情况下仿真参数相同。仿真结果如图7~图10所示。 由图7~图8可知,在机械臂起始位置含初态误差的情况下,PD型迭代学习控制方法在迭代10次后,轨迹跟踪效果明显好于此方法第1次跟踪,但仍不能实现对期望轨迹的精准跟踪。无论是第1次迭代还是10次迭代之后,本文的PD型迭代滑模控制算法都能在很短的时间内在迭代域实现对期望轨迹的精准跟踪。 图7 机械臂第1次迭代位置跟踪曲线图 图8 机械臂第10次迭代位置跟踪曲线图 分析图9~图10可知,使用PD型迭代学习控制算法的机械臂在首次对期望轨迹跟踪时,其跟踪误差在迭代域收敛极慢,关节1跟踪误差甚至出现不收敛的情况,在10次迭代后,其误差收敛速度得到一些改善,但收敛过程几乎充满整个迭代域,依然无法满足机械臂在生产场景中的应用。而本文的PD型迭代滑模控制算法能实现将初态误差在很短的时间内收敛到接近零,保证机械臂在很短(0.4 s)的时间内完全跟踪上期望轨迹。实现了在迭代域[δ,T]内对输入轨迹的精确跟踪。从迭代域轨迹跟踪误差的收敛速度和实现轨迹精确跟踪所需的迭代次数来看,本文的PD型迭代滑模控制算法都明显优于PD型迭代学习控制算法。 图9 机械臂第1次迭代位置跟踪误差曲线 图10 机械臂第10次迭代位置跟踪误差曲线 (1)在不含初态误差的机械臂轨迹跟踪过程中,与PD型迭代学习控制算法相比,PD型迭代滑模控制算法具有在迭代域误差收敛速度快的优点,且能在较少次迭代的情况下实现对期望轨迹的精确跟踪。 (2)在含有初态误差的机械臂轨迹跟踪过程中,PD型迭代学习控制无法实现对期望轨迹的精确跟踪,PD型迭代滑模控制算法可以克服这一缺点,在最初很短的时间经过调节,实现在迭代域[δ,T]内对期望轨迹的精确跟踪。在含有扰动的情况也能保持对期望轨迹的精确跟踪,表明设计的算法具有较强的鲁棒性。 (3)仿真试验中增大滑模控制项比例系数,能缩短机械臂在含初态误差下轨迹跟踪调整时间。但滑模项比例系数过大会造成短时间内控制力矩激增,对机械臂产生冲击,且速度跟踪误差会增大。在实际应用场景中需考虑机械臂动作限制条件,合理调节各项系数。2 控制律设计与收敛性分析
2.1 控制律的设计
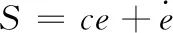



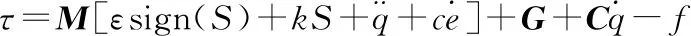
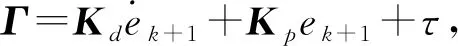
2.2 收敛性分析



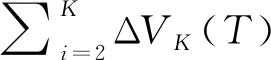


3 仿真验证

3.1 无初态误差下控制仿真分析


3.2 含初态误差下控制仿真分析
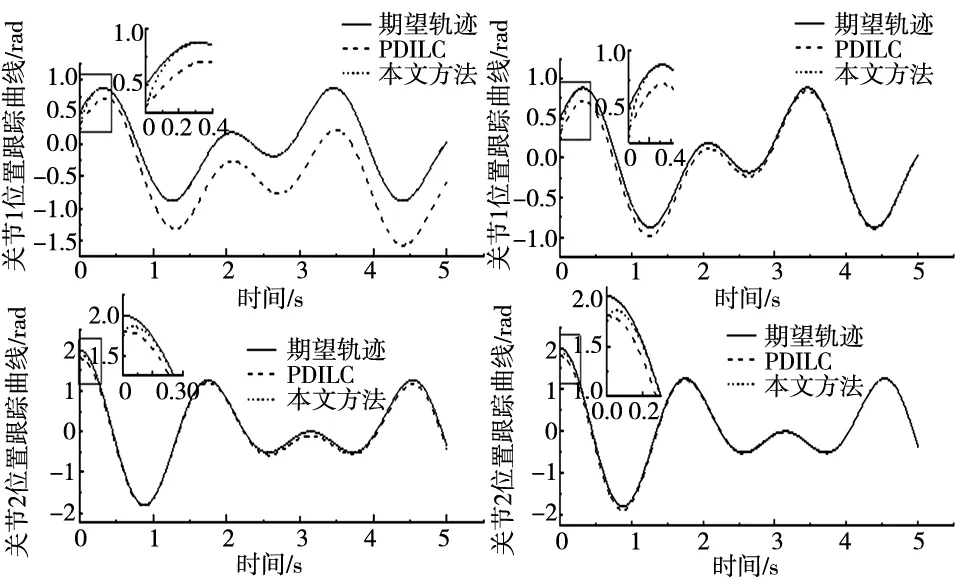

4 结束语
