融合轨迹规划的力矩前馈补偿方法*

陈 琳，陈博扬，陈 韬，许纪湖，潘海鸿

(1.广西大学机械工程学院，南宁 530004；2.广西安博特智能科技有限公司，南宁 530000)

0 引言

要实现机器人高精运动性能，需结合机器人动力学特性进行控制。常用提高机器人控制精度的有效方法是基于动力学模型的力矩前馈控制算法[1-3]。该算法包括机器人动力学建模、参数辨识和力矩前馈补偿方面的研究。动力学建模常用方法有牛顿欧拉法、拉格朗日法等。参数辨识常用的算法主要有各类最小二乘法[4- 5]、极大似然法[6]以及人工智能算法[7-8]。

ABDELLATIF等[9]在传统的PID控制的基础之上增加力矩前馈控制，通过机器人动力学模型计算出机器人各关节所需力矩，利用力矩电流转换关系，将机器人关节力矩转换为电流环前馈值叠加到电流环上，提高末端轨迹跟踪精度。姚祥[10]添加基于负载惯量匹配的力矩补偿控制，提高带载工况下机器人末端位置跟踪精度，改善其动态性能。张铁等[11]建立机器人刚柔耦合动力学模型，计算出柔性关节所需的前馈力矩值并叠加到电流环，使机器人末端振动加速度幅值下降60%，提高机器人末端的定位精度。

上述研究均是将辨识模型的计算力矩直接叠加到电流环进行力矩前馈补偿。但由于动力学模型的复杂性，辨识精度仍无法满足实际应用的需要，特别是低速和换向时辨识误差较大，进一步提高辨识模型的精度较为困难。为此，提出一种融合轨迹规划的力矩前馈控制算法。该算法在基于动力学模型的力矩前馈补偿的基础上，充分考虑轨迹规划各个运动段的动力学模型辨识精度的差异，对运动轨迹中辨识精度较差的运动段的模型计算力矩进行修正处理，并将其叠加到电流环，改善力矩前馈补偿效果，提高轨迹跟踪精度。

1 动力学建模与参数辨识

1.1 动力学建模

采用牛顿欧拉法建立m自由度串联型工业机器人的动力学模型：

(1)

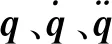
根据文献[5]，机器人线性化动力学模型为：

(2)

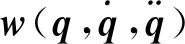
φi=(Ixxi,Ixyi,Ixzi,Iyyi,Iyzi,Izzi,mxi,myi,mzi,mi,fci,fvi)T

(3)

式中，Ixxi、Ixyi、Ixzi、Iyyi、Iyzi、Izzi为连杆i相对于其关节坐标系的惯性张量；mxi、myi、mzi为连杆i相对于其关节坐标系的一阶质量矩；mi为连杆i的质量；fci为库伦摩擦系数；fvi为粘滞摩擦系数。

基于MD-H坐标系通过机器人最小参数重组递推公式可确定机器人的一组最小参数集，机器人只包含最小惯性参数的动力学模型：

(4)

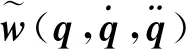
1.2 参数辨识

机器人动力学参数辨识一般包含激励轨迹设计、数据采样及处理、参数估计和模型验证4个步骤，具体如下：

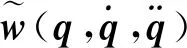
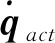
(5)

步骤4：用不同于激励轨迹的轨迹作为验证轨迹来对辨识结果的精度进行验证：对比验证轨迹实际力矩τact和辨识模型计算力矩τcal的拟合情况，验证辨识精度。

2 融合轨迹规划的力矩前馈补偿策略

为提高轨迹跟踪精度，对上述算法进行改进，提出融合轨迹规划的力矩前馈补偿控制算法(以下称改进补偿)，如图1所示。在直接补偿的基础上，充分考虑轨迹规划各个运动段的动力学模型辨识精度的差异，对辨识精度较差的运动段的模型计算力矩进行修正处理后再叠加到电流环，提高轨迹跟踪精度。

图1 融合轨迹规划的力矩前馈补偿控制算法

图2 S形加减速轨迹曲线

(6)

式中，τim为改进后的计算力矩(以下称改进力矩)；ts为τim(ts)=τcal(ts)的时间；k1为力矩缓慢加载斜率。

在减速段，因摩擦力模型在启动段和停止段有一定差异，提出在该段对摩擦力模型进行修正：

(7)

式中，修正符号函数如下：

(8)

匀加速段和匀减速段的加速度为系统允许的最大值；减加速段和加减速段加速度变化大，位置变化快。这四段对应的动力学模型中各项力矩均起作用，直接将计算力矩τcal作为前馈量叠加到伺服驱动器电流环(图1)。但匀速段加速度为0，电机驱动力矩与重力矩和摩擦力矩处于平衡状态，重力矩与摩擦力矩变化慢，伺服三环控制精度高。因此提出匀速段不采用力矩前馈补偿。

3 实验验证与分析

3.1 实验平台

实际工程应用中的机器人多为串联型六自由度工业机器人，现以单关节为研究对象。搭建如图3所示的单轴实验平台模拟机器人单关节(m=1,i=0)。该平台上位机采用RTX运动控制器，数据下发与采样周期均为1 ms。采用松下(MADLN05BE和MSMD012G1V)伺服驱动系统，电机额定转速为3000 r/min，额定转矩为0.32 N·m，减速比N=80。

图3 单轴实验平台

首先，通过动力学参数辨识实验得到单轴平台不同负载下的动力学参数；其次，为验证改进补偿算法的有效性进行如下实验测试：①进行不同补偿方式(无力矩前馈补偿、直接补偿和改进补偿)下的力矩前馈补偿实验测试；②相同负载不同速度下的改进补偿实验测试；③相同速度不同负载下的改进补偿实验测试；④具有匀速段轨迹不同补偿方式力矩前馈补偿实验测试。

3.2 动力学参数辨识实验及验证结果

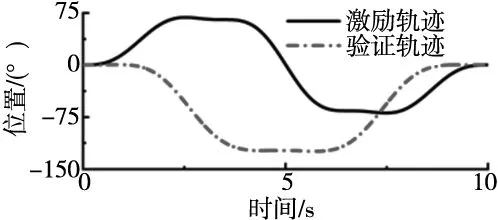
图4 单轴平台辨识轨迹及验证轨迹

表1 单轴平台动力学参数辨识结果

图5为辨识精度的验证结果，单轴平台(负载1)辨识模型计算力矩误差整体较小，但在低速段力矩误差较大，速度换向处出现误差峰值，模型计算力矩与实际力矩拟合程度很差。负载2、3的辨识精度与负载1类似，在非低速段及非速度换向处的辨识精度较高。

(a) 力矩拟合曲线(b) 力矩拟合误差曲线

3.3 力矩前馈补偿实验结果与分析

(1)不同补偿方式力矩前馈补偿：单轴平台带负载1分别运行规划的3种不同速度运动轨迹，如图6所示。采集无力矩补偿的实际力矩，以及无力矩补偿、直接补偿和改进补偿的位置跟踪误差如图7和表2所示。

图6 单轴平台3种不同速度轨迹

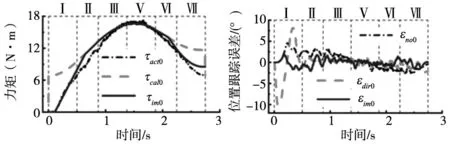
(a) 力矩图(轨迹1) (b) 位置跟踪误差图(轨迹1)

表2 实验(1)位置跟踪误差均方根和极值

图7中，τact0为无补偿力矩，τcal0为计算力矩，τim0为改进力矩，εact0为无补偿位置跟踪误差，εdir0为直接补偿位置跟踪误差，εim0为改进补偿位置跟踪误差。改进力矩较计算力矩与实际力矩拟合程度有很大提升，且改进补偿算法位置跟踪误差冲击减小。由表2可知，改进补偿较无力矩补偿，位置跟踪误差均方根随速度的增加分别减少57.71%、64.66%、69.74%；改进补偿较直接补偿，位置跟踪误差均方根随速度的增加分别减少69.85%、64.95%、56.86%。

(2)相同负载不同速度改进力矩前馈补偿：采用改进补偿算法在单轴平台(负载2)运行图6中不同速度运动轨迹，获取位置跟踪误差如图8和表3所示。图8改进补偿轨迹跟踪精度有明显提高，位置跟踪误差均方根和极值减小比例随速度的增加明显下降。

(a) 轨迹1 (b) 轨迹2

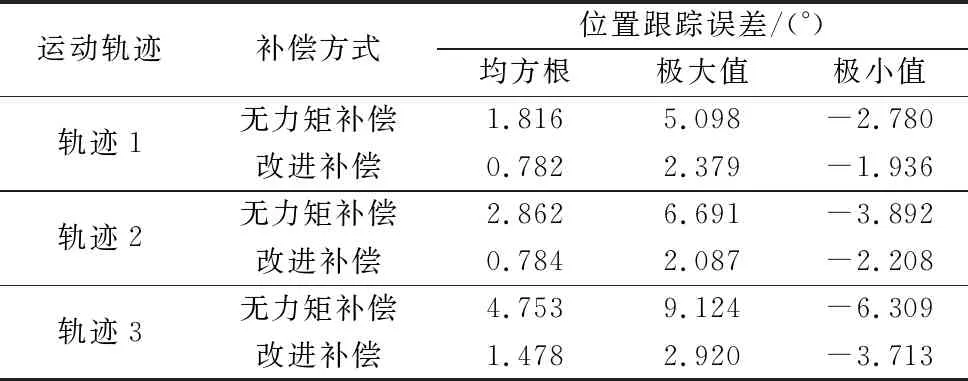
表3 实验(2)位置跟踪误差均方根和极值

(3)相同速度不同负载改进力矩前馈补偿：单轴平台(带负载1、2、3)运行图6运动轨迹2，采集位置跟踪误差如图8和表4所示。

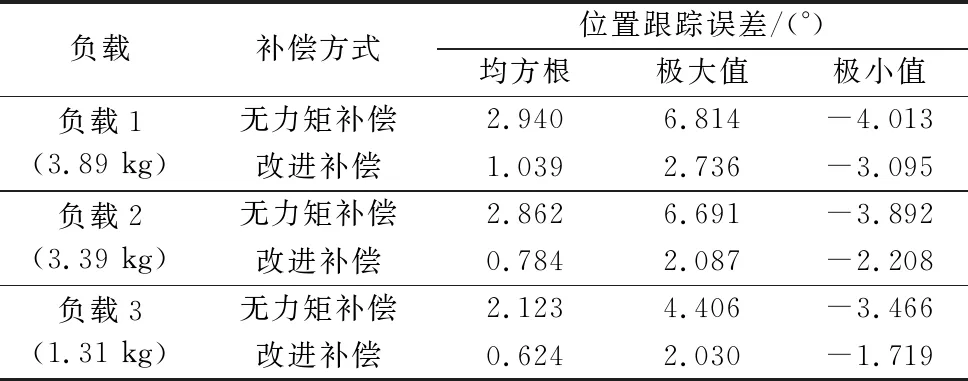
表4 实验(3)位置跟踪误差均方根和极值

由图8和表4可知，改进补偿后随负载的增加位置跟踪误差均方根分别减少64.66%、72.61%、70.61%。

(4)具有匀速段轨迹不同补偿方式力矩前馈补偿：单轴平台(负载1)运行图9规划轨迹，采集无力矩补偿、直接补偿和改进补偿位置跟踪误差如图10所示。

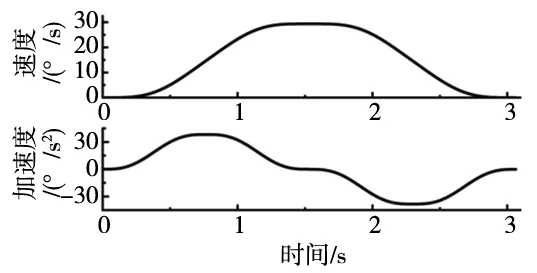
图9 正弦加减速轨迹曲线

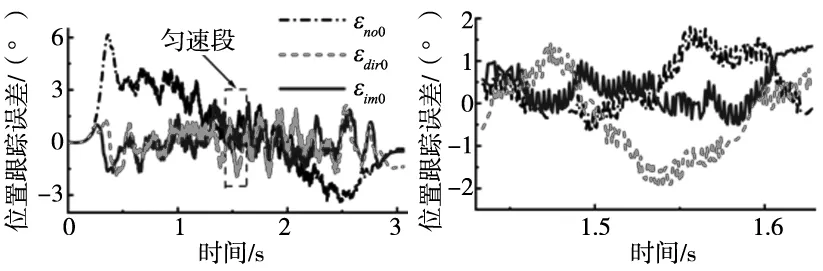
(a) 位置跟踪误差 (b) 匀速段位置跟踪误差

图10和表5匀速段改进补偿后较无力矩补偿和直接补偿位置跟踪误差均方根分别减小52.82%，66.64%。

表5 匀速段不同补偿方式跟踪误差均方根和极值

综上所述，改进补偿算法修正后力矩与实际力矩拟合程度更好，有效提高轨迹跟踪精度。伺服三环调节存在滞后，高速重载情况下改进补偿效果更为明显。匀速段重力矩和摩擦力矩与电机实际力矩处于平衡状态，且匀速段重力矩与摩擦力矩的合力矩变化慢，伺服三环控制精度高，因此改进补偿后轨迹跟踪精度提高。

4 结论

本文针对基于动力学模型的力矩前馈补偿策略在低速段等特定运动段轨迹跟踪精度较差的问题，对动力学力矩前馈补偿算法进行改进，提出融合轨迹规划的力矩前馈补偿控制策略，提高轨迹跟踪精度。从单轴实验平台的实验测试可知，该算法较无力矩前馈补偿位置跟踪误差均方根减小50%以上，且较直接补偿算法冲击明显减少。表明该方法能够有效提高机器人单关节的轨迹跟踪精度。