低速重载NNF轴承动态特性分析*
2022-11-25陈西忍叶文华
陈西忍,叶文华,伍 毅
(1.南京航空航天大学机电学院,南京 210016;2.安徽工业大学机械工程学院,马鞍山 243000)
0 引言
NNF轴承作为冶金生产线的关键部件之一,常用于低速重载工况,例如冷轧机、热轧机、卷取机、开坯机等轧钢机机械上,不仅所处的工作环境温度高,而且工作过程中承受着巨大的冲击和载荷,若轴承设计和使用的不合理,很可能导致轴承的零部件提前失效而使整个轴承提前失效,造成整条冶金生产线停止运行,不仅耽误生产进度,还会增加生产成本。研究表明,与滚动轴承的精度和寿命相关的两个相互依赖的关键特性参数是接触应力和变形,但这两个关键特性参数很大程度上受限于工作载荷和转速[1-4]。近年来,国内外学者和专家为了防止轴承提前失效,已经对轴承的动态特性做了大量的研究工作。
万超等[5]构建了高转速下角接触球轴承的几何和受力平衡关系式,研究了外载荷和转速对轴承疲劳剥落的影响。李德水等[6]分析了高转速下角接触球轴承的不同结构参数和工况参数对轴承动态特性的影响。徐涛等[7]建立了轴承结构模型,通过仿真分析了联合载荷对接触应力、接触应变的影响规律。ZHENG等[8]通过数值模拟研究了振动载荷和转速等参数对双列圆锥滚子轴承疲劳寿命的影响规律。CAI等[9]建立了高转速下角接触球轴承应力分析的通用数学模型,分析了载荷条件和转速对刚度特性、接触变形等轴承参数的影响。卢黎明等[10]通过建立的滚滑轴承模型分析了在启动和稳态运转过程中的轴承内部的动态接触应力的变化规律。
可以看出,国内外学者的研究大多是对高速轻载轴承进行动态特性分析,很少有学者对恶劣工况下的低速重载轴承的最大接触应力和变形进行数学模型与有限元相结合的分析。因此,本文首先建立NNF轴承的数学分析模型,包括载荷与变形关系式、变形协调方程和受力平衡方程。通过求解该模型,可以求得NNF轴承的动态负荷分布和滚子与内外圈的变形,同时使用ANSYS Workbench对满载轴承进行瞬态动力学分析,得出了轴承的内外圈与圆柱滚子之间的接触应力和变形,通过结果对比验证建立的数学模型。最后分析径向载荷与转速对滚子与轴承内外圈的最大接触应力和总变形的影响规律。为NNF轴承的设计和使用提供了参考,对提高NNF轴承寿命和提升冶金传动系统的工作可靠性具有重要意义。
1 理论分析
1.1 载荷—变形关系式
NNF轴承中的滚子与内外圈滚道间为线接触,我们一般采用近似或者经验计算公式。陈家庆等[11]详细的对各种线接触问题中的弹性趋近量近似计算公式的精度进行了对比,得出的A.Palmgren经验公式是目前国内轴承行业常用的有效计算式,本文也选择采用这一经验公式。圆柱滚子与内外圈接触处的变形量可用式(1)计算:
(1)
式中,Q为外载荷,kN;lt为滚子的有效接触长度,mm;E1、E2、μ1、μ2为两接触体的弹性模量,GPa和泊松比。
1.2 变形几何协调方程

图1 轴承变形分布示意图
假设0号滚子位于轴承的最底端,其弹性变形δ0仅作为计算的中间变量,在建立它与其它滚子和内外圈的变形协调方程时,不考虑内外圈的弯曲变形和油膜厚度的影响,仅计算接触处的弹性变形,则0号滚子的最大接触变形量为:
(2)
式中,δo0和δe0表示0号滚子与外圈、内圈的接触变形量。
结合图1,根据几何协调变形关系[11]可得:
(3)

(4)

(5)
δi=δoi+δei=δrcosφi-ur/2
(6)
式中,δoi和δei表示第i个滚子与外圈、内圈的接触变形量;尽管式(6)是在图1中径向游隙为正时分析所得,但若对负游隙时做同样的分析,仍可得到该式。若游隙为负,则需|ur|<2δ0成立,式(6)才有意义。
1.3 力学平衡方程
如图2所示,φj为接触区半角;d为滚子外径;De为外圈外径;do为内圈内径;Dm为滚子组的节圆直径;Fc为滚子受到的离心力。

图2 轴承载荷分布示意图
在任意角φi处,假设轴承只承受径向力,内、外圈与滚子间的法向作用力分别为Fei、Foi。外圈固定,内圈转速为ni,在径向力Fr作用下,轴承内圈的受力平衡方程[12]为:
(7)
式中,Z为接触的滚子数。
滚子的受力方程:
Foi-Fei-Fc=0,(i=1,2,…,Z)
(8)
滚子受到的离心力Fc可表示为:
(9)

采用Newton-Raphson法迭代求解式(1)、式(3)、式(5)~式(7),可以得到滚子轴承的载荷分布。
2 有限元分析
2.1 几何模型的建立及简化
如图3a所示,以某公司热轧板生产线上卷取机中使用的NNF轴承为例。轴承内圈是以十字轴轴颈作为支撑滚道,使轴系布置更加紧凑。滚子与轴承套和十字轴相接触,轴承套作为轴承外圈(以下称十字轴轴颈为轴承内圈,轴承套为轴承外圈),十字轴轴端装有一个推力轴承,用于承受轴向力,轴承由骨架油封和一些密封垫圈进行密封,实际工况比较恶劣,接触状态也很复杂。
为了方便计算,尽可能得出NNF轴承最真实的实验结果,可以在建模时对某些部位进行适当的简化:①考虑到轴承内、外圈上的边楞倒角和圆角对轴承整体的接触应力和变形影响不大,在建立模型时将其省去,简化内外圈和滚子;②本文主要研究的是径向载荷和转速对NNF轴承接触应力和变形的影响,工作过程中产生的轴向力由十字轴轴端顶部的推力轴承承受,所以在对轴承进行建模时可以忽略推力轴承;③分析的是一副轴承,所以只保留十字轴的一个轴端,忽略润滑作用以及油膜的影响,省略了骨架油封。然后根据表1所示NNF轴承的主要几何参数对轴承进行简化建模,建立的简化模型如图3b所示。

(a) 十字轴模型 (b) 轴承简化模型
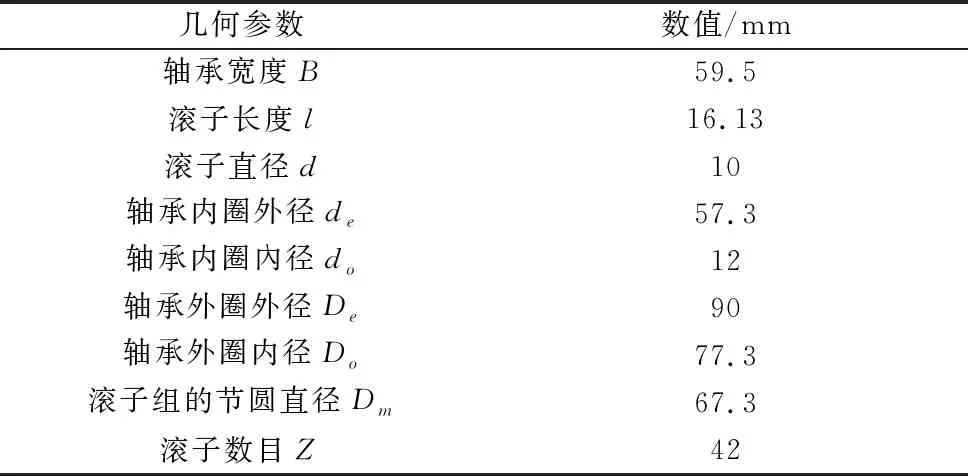
表1 NNF轴承的几何参数
2.2 轴承有限元建模
(1)定义材料属性。轴承零部件的材料属性如表2所示。

表2 轴承零部件材料参数
(2)运动副和接触设置。在对NNF轴承进行分析时,首先需要确定的链接关系包括运动副和接触。在施加运动副时,考虑到轴承外圈与万向联轴器的法兰叉和焊接叉是紧密接触的,所以将外圈表面设置为fixed;内圈设置为General,约束其沿Z方向移动和X、Y方向的转动。在设置接触时,根据接触面和目标面的选择原则,通常把滚子之间与滚子(contact)和内外圈滚道面(target)之间的接触设置为frictional,其中滚子之间的摩擦系数取0.05,滚子与内外圈之间的摩擦系数取0.1,滚子端面和端面之间与滚子端面和轴承外圈端面内表面之间的接触设置为Frictionless[13]。
(3)网格划分。综合考虑轴承简化模型的整体情况,对轴承内外圈进行四面体网格划分,滚动体采用六面体网格划分,为保证接触区域的计算精度,对滚子面和滚子与轴承内外圈的接触面的网格进行局部细化,设置网格尺寸为3 mm,总共生成18 364个单元,52 519个节点,建立的有限元网格模型如图4所示。

(a) 滚动体的网格 (b) 轴承整体模型网格
(4)载荷与边界条件。卷取机工作过程中,轴承承受不均匀的载荷,受力状态复杂。通过对现场拆卸下来的滚子的失效情况进行分析,发现大部分滚子有不同程度的点蚀现象,根据十字轴沿轴线方向磨痕均匀,且靠近十字轴轴肩圆弧处磨痕最深,朝两端方向上磨痕逐渐减小,如图5所示。
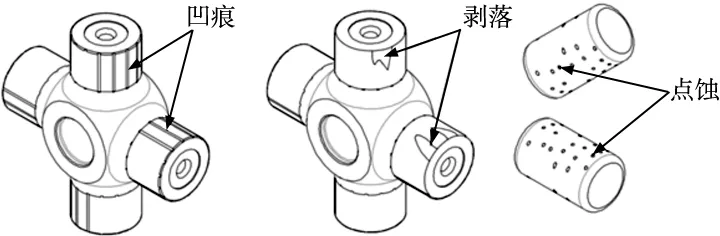
图5 轴承失效类型示意图
如图6所示,其中图6a为轴承内圈受力示意图,图6b为轴承外圈受力示意图。在施加载荷过程中,可以将轴承内圈所受的径向载荷简化为正弦规律变化分布的载荷,其中载荷p1=p0sinα(0≤α≤180°)。已知传递的额定转矩Tc为2.6×104kN·mm,则作用在轴承上的径向分布载荷的合力为:

(a) 十字轴受力简图 (b) 轴承上径向载荷分布
图6 内外圈受力示意图
所以对轴承内圈外表面施加的径向轴承载荷为178.4 kN。如表3所示,使用分步加载的方式对轴承经行加载,有利于结果分析。同时对轴承内圈施加10 r/min的转速,转换为弧度制大约为1 rad/s。设置好载荷和约束的轴承模型如图7所示。

图7 设置好载荷和约束的轴承模型

表3 分布载荷施加
因为轴承的接触是非线性实体接触,接触算法采用的是增强拉格朗日法,为防止可能出现的收敛问题,调整接触刚度和模型的初始间隙。在求解设置中,打开自动时间步、弱弹簧和大变形开关,设置好初始步数(initial substeps)、最小步数(minimum substeps)和最大步数(maximum substeps)。相应的求解设置设定好后进行求解。
2.3 计算结果分析
求解得到的NNF轴承整体和各零部件单独的接触应力和变形云图如图8和图9所示。

(a) 轴承 (b) 滚子

(a) 轴承整体 (b) 滚子
可以看出以10 r/min转动的NNF轴承在178.4 kN径向载荷的作用下(满载),整体的最大接触应力为957.44 MPa,最大变形量为1.492 3 mm,其中内圈的最大接触应力为447.41 MPa,出现在施加径向载荷的内圈内表面,其值小于轴承内圈材料的屈服强度1292 MPa;外圈的最大接触应力为355.21 MPa,出现在滚子与外圈滚道相接触的地方,其值小于轴承外圈材料的屈服强度850 MPa;滚子的最大接触应力为957.44 MPa,出现在径向载荷下方滚子与外圈滚道相接触的地方,其值小于滚子材料的屈服强度1459 MPa,三者都满足工程实际的需求。但是滚子的最大接触应力要远大于内圈和外圈的最大接触应力。根据ISO76-2006的标准规定[14],滚子轴承的内部接触应力应小于4000 MPa,虽然该轴承的接触应力符合许用抗拉和抗压强度要求,但是该轴承在实际工作中轴承的整体应力是分布不均的,且已经证明轴承寿命与应力的七次方成反比(甚至更高)[15]。所以NNF轴承在满载运行的过程中,滚子表面和十字轴轴端表面很容易发生材料的疲劳和强度破坏以致引起滚动轴承的各种故障[16]。且随着转速和径向载荷的增加,失效的可能性会越来越大[17]。
统计结果表明,大部分NNF轴承失效都是因为滚子失效,而且失效的程度也不一样,选取其中两副轴承里的滚子失效情况如表4所示,调查结果与上面的仿真结果相符合。

表4 滚子失效情况统计
2.4 数学模型仿真实验验证
本文提出用A.Palmgren经验公式作为NNF轴承的弹性趋近量近似计算公式,为了验证提出公式的准确性,计算NNF轴承在0~178.4 kN线性变化的纯径向载荷作用下的总变形量,并用式(1)计算出NNF轴承在不同径向载荷下的最大变形量,得出的结果如图10所示。

图10 理论和仿真实验结果对比
可以看出在正常的径向载荷下(即40 kN~178.4 kN),NNF轴承的总变形量的理论计算值与仿真值比较吻合,二者最大误差小于9%;径向载荷低于40 kN时,理论计算与仿真值相差悬殊,这是因为一般冶金传动生产线上使用的NNF轴承都存在游隙,所以内外圈一开始会在径向载荷的作用下发生相对位移。随着径向载荷的施加,当滚子与内外圈接触时,滚子与内外圈之间开始产生接触变形,此时NNF轴承的最大变形随载荷的变化才回归正常的状态。
可见,在适当的载荷下,两种计算方式得到的数据误差都在工程的允许范围之内,且分析结论与实际轴承受力破坏情况相符,也就是说理论计算与ANSYS仿真互相验证了彼此的正确性和可行性,证实了理论模型与有限元模型的正确性。
2.5 接触应力和变形分析
由上面的理论和仿真计算都可以得出径向载荷和转速对轴承的接触应力和变形有较大的影响,通过仿真对不同径向载荷和转速工况下的NNF轴承的接触应力和变形的影响规律进行了分析。
(1)转速对接触应力和变形的影响。如图11所示,保证对NNF轴承施加的径向载荷(额定径向载荷为178.4 kN)不变,得出了不同转速工况下最大接触应力和总变形(滚子、内圈和外圈的变形之和)的变化曲线。可以看出,NNF轴承滚子与内外圈的最大接触应力和总变形都随着内圈转速一起增加,而且增加的速率越来越快,呈现出指数型增长趋势。其主要原因是NNF轴承在运行过程中,随着NNF轴承转速的增加,滚子的离心力也越来越大,同时滚子与内外圈的循环接触会造成轴承弹性变形量的累积,从而造成转速越快,最大接触应力和总变形量增加越快[18],容易导致轴承失效的时间不可预测。
(2)径向载荷对接触应力和变形的影响。如图12所示,保持NNF轴承的额定工作转速(1 rad/s)不变,得出了不同径向载荷工况下滚子与内外圈的最大接触应力和总变形的变化曲线。可以看出,随着NNF轴承径向载荷的缓慢增加,滚子与内外圈的最大接触应力和总变形都在线性增加,这也验证了在中等径向载荷下,轴承的变形量理论计算值与仿真值比较吻合。如果NNF轴承长期在过载的工况下使用时,其总变形和最大接触应力值会一直处于材料屈服强度的边缘,容易导致轴承失效,进而引发事故。
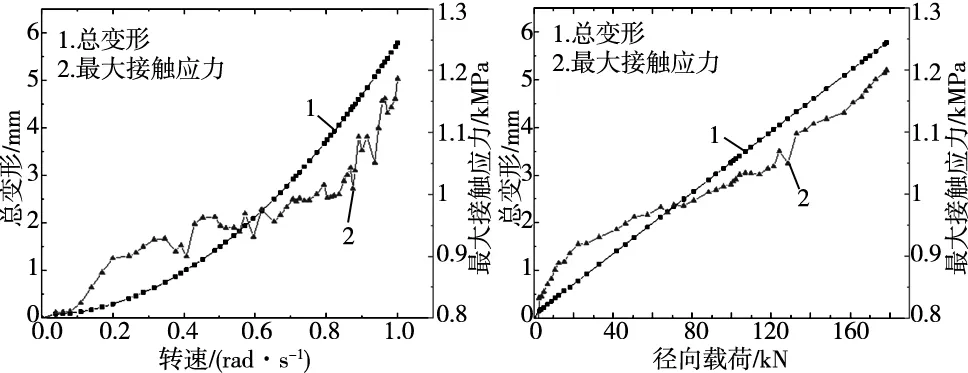
图11 最大接触应力与总 变形随转速变化图 图12 最大接触应力和总变 形随径向载荷变化图
3 结束语
本文以某轧钢厂热轧板线卷取机用万向联轴器中使用的NNF轴承为例,建立其数学分析模型,采用瞬态动力学方法分析了径向载荷和转速对接触应力和变形的影响,得出了以下结论:
(1)验证了额定工况下建立的数学模型和有限元模型具有较好的一致性,A.Palmgren经验公式同样可以作为NNF轴承在静态下的变形量近似计算公式。
(2)转速对NNF轴承接触应力和变形的影响远大于径向载荷,所以要尽量避免在超过轴承额定转速的工况下使用这种重载轴承。
(3)滚子整体的接触应力要远远大于轴承内圈和外圈的接触应力,所以在对这种重载轴承进行设计或者优化时,不仅需要考虑轴承承受的径向载荷和转速,还需要着重考虑滚子与轴承内圈的接触应力和变形情况,保证NNF轴承的等强度设计。
