基于课程思政的“随机抽样”教学实录*

2022-11-25刘品德邹庆榕

中学数学杂志 2022年8期

刘品德马瑛邹庆榕

(广东省江门市培英高级中学 529000)

数学课程思政是指“数学课程在立德树人的落实上所具有的独特的德育价值”[1].因此，实施数学课程思政，就是充分挖掘数学课程的育人价值，特别是德育价值，并在教学实践中加以实现.数学课程思政既让学生了解数学与生活息息相关，又能培养学生的理性思维和应用意识.本文从数学课程思政的角度实施“随机抽样”教学，在知识传授的同时，充分挖掘课程中的思政元素，又为学生搭建一个从认知到理性认识的桥梁，从而润物无声地践行数学学科德育思政.

1 教学目标与实录

1.1 教学目标

(1)借助多媒体创设情境，寓教于乐，使学生在实际情境中亲身体会感受随机抽样，区分普查与抽查、抽签法与随机数法的异同及优点与不足.

(2)在小组探究、合作交流的过程中，增强团队意识和合作共赢的理念，培养和发展用数学的眼光去观察世界、用数学语言去表达世界的能力.

(3)体会普查与抽查、抽签法与随机数法间的关系，培养理性精神，增强自主探究与发现的能力和自信心，感悟数学的应用价值，进而激发学好数学的兴趣和激情.

图1

1.2 教学实录

·生活实践，引入“普查”

师：(多媒体演示) 图1是什么活动？

生：人口普查！

师：对！今天咱们就从人口普查开启本课的数学之旅！

师：开展人口普查，是推动经济高质量发展的内在要求.像人口普查这样，对每一个调查对象都进行调查的方法，我们称为——

生：全面调查，又称普查.

师：第七次人口普查既能摸清家底，又是完善人口发展战略和政策体系、促进人口长期均衡发展的迫切需要.

师：在一个调查中，我们把调查对象的全体称为总体，组成总体的每一个调查对象称为个体.由于不同调查对象的指标值往往不同，称之为变量，因此，为了强调调查目的，也可以把调查对象的某个指标的全体作为总体，每一个调查对象的相应指标作为个体.比如，要调查全国人口男女比例，那就以性别指标进行调查.

图2

设计意图从学生亲身经历的第七次全国人口普查，科普人口普查的重大意义，学习相关数学概念，激发学生学习兴趣，感受理论来源于生活实践，宣传国家的大政方针.

·小组讨论，认识“抽样”

师：近几年，人们最为关注的焦点是什么？(出示图2)

生：新冠肺炎疫情和疫苗.

师：没错.中国新冠疫苗研发国际领先，但西方国家对中国疫苗态度双标.检验疫苗有效性，是不是得每一剂都打完？

生：不是，抽一部分检验.

师：对！从总体中抽取一部分个体进行调查，并以此为依据对总体的情况作出估计和推断的调查方法，称为抽样调查.从总体中抽取的那部分个体称为样本，样本中包含的个体数称为样本容量，简称样本量.调查样本获得的变量值称为样本的观测数据，简称样本数据.

图3

师：如图3，大家从媒体上已了解过2021年巴西布坦坦研究所启动的“S计划”，这是为当地所有18岁以上民众接种中国科兴疫苗，当地的疫情很快得到控制，巴西小镇“成了奇迹”.这证明中国疫苗是有效的，很快世界卫生组织宣布将中国国药集团的新冠疫苗列入紧急使用清单，对全球抗疫作出中国贡献.这种抽样调查花费少、效率高.

设计意图结合实例让学生比较“全面调查”与“抽样调查”，感知在有些调查中，抽样调查具有不可替代的作用.同时，让学生对复杂的国际形势有所了解．

师：科技无国界，但科技新产品是属于不同国家的.正是因为有强大的祖国上下一心，我们才取得了令全球瞩目的抗疫成效，同学们要努力学习，为我国的科技发展多作贡献.

·合作探究，深化理解

师：抽样调查的应用范围越来越广，通过抽样调查了解总体，自然希望抽取的样本数据能很好地反映总体的情况，即样本含有和总体基本相同的信息.我们主要研究两种基本的抽样方法──简单随机抽样和分层抽样.

师：为保证节假日食品安全，都要抽查食品，说说有哪些重点检查项目？

生：生产日期、重金属、微生物、食品添加剂(色素、防腐剂、甜味剂)、农药残留……

设计意图从生活中的案例讨论，让学生关注食品安全，抽样调查在生活中随处可见，也为随机抽查等相关概念的学习作好铺垫.

师：一般地，设一个总体含有N(N为正整数)个个体，从中逐个抽取n(1≤n≤N)个个体，如果抽取是放回的，且每次抽取时总体内的各个个体被抽到的概率都相等，我们把这样的抽样方法叫做放回简单随机抽样；如果抽取是不放回的，且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等，这样的抽样方法叫做不放回简单随机抽样.两者统称为简单随机抽样.通过简单随机抽样获得的样本称为简单随机样本.

讨论：从总体中逐个不放回地随机抽取n个个体作为样本与一次性批量随机抽取n个个体作为样本是不是等价的？

生1：不是等价的，原因是两种抽取方式的样本中个体被抽取的可能性不同.

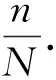
师：两种方式是等价的，我们可以证明这两种方式中各个个体被抽到的概率相等.本章的简单随机抽样都是指不放回简单随机抽样.实现简单随机抽样的方法有很多，我们主要学习抽签法和随机数法两种常用方法.

设计意图比较两种简单随机抽样方式，使学生理解它们的等价性，为后续学习用样本估计总体及概率计算作好准备.

·领悟要点，比较异同

师：我们年级有1 020位同学，要从中抽取50位同学估计本年级学生的身高，为使样本平均身高接近全年级同学的平均身高，如何选择样本？

生：①编号0001～1020(也可以用学号)； ②制号签(写在小纸片上后揉成团)；③放入不透明盒子中充分搅拌；④抽签得到样本.

师：对！这就是抽签法.当个体比较多时，制签就比较麻烦，这时我们可以考虑使用随机数法：①编号0001～1020(也可以用学号)；②用随机试验生成随机数或从随机数表中读取样本编号；③生成样本.

图4

师：我们了解以下随机试验.

①小球试验：同学们课后可以观看CCTV2福彩开奖，如图4.各小组进行模拟试验，用10个乒乓球，上面写上0，1，2，3，…，9，放入一个不透明的袋子里，充分搅拌后有放回地摸取4个球，分别作为千、百、十、个位数，这样就生成了一个四位随机数，如果在0001～1020内，就代表对应编号的学生被抽中，否则认为是无效号，同时，如果出现重复也视为无效，应舍去.

②用信息技术生成随机数：计算器生成随机数，电子表格生成随机数，用R统计生成随机数等.其中电子表格生成随机数的实验就可以在信息技术课上完成，在电子表格的任一单元格中输入“=RANDBETWEEN(1，1 020)”即可生成一个1～1 020范围内的整数随机数.

③从给定的随机数表中读取样本.

例1从编号依次为01，02，03，…，20的20人中选取5人，现从随机数表的第一行第3列和第4列数字开始，由左向右依次选取两个数字，则第五个编号为( ).

5308 3395 5502 6215 2702 4369 3218 1826 0994 7846

5887 3522 2468 3748 1685 9527 1413 8727 1495 5656

A.09 B.02 C.15 D.18

生：错选B或C(没有注意所选号是不是都在01～20)；错选D(没有考虑到重复的02号)

设计意图结合学生比较关心的身高问题介绍抽签法和随机数法，产生随机数的小球试验容易操作，学生也有兴趣，小组动手实验；电子表格也是学生比较熟悉的，可以在信息技术课上完成；其他两种方法只作一般介绍.例题解答暴露学生使用随机数法容易犯的几种错误.

师：我们知道，在重复试验中，试验次数越多，频率接近概率的可能性越大，如抛硬币试验.与此类似，用简单随机抽样的方法抽取的样本容量越大，样本中占比接近总体中占比的可能性越大，因此，样本量大的会好于样本量小的，普查是最有代表性的，但不可否认抽样调查的作用，抽样调查中样本量的选择要根据实际问题的需要，并不一定是越大越好.

师(小结)：为了更好理解今天的学习内容，我们可以作以下对比：普查和抽样调查的对比；抽签法和随机数法的对比.

2 几点反思

2.1 “课程思政”的理念要自然融入

本节课从全国人口普查导入，使学生对人口普查的重要意义有进一步的认识，再到我国新冠疫苗在巴西试验成功，让学生认识科技的力量和抽样调查的必要性.本课将德育渗透在教学的每一个环节，实现了帮助学生形成理性思维、激发积极情感、树立正确信念、培养优秀品质的目标.

2.2 “课程思政”在数学实践应用中应该得到重视

数学和其他科学知识一样来源于实践、应用于实践，并在实践中得到发展，很多的优秀教学设计呈现的PPT只是概念的文字呈现，没有一点“温度”[2].本节课从学生的亲身经历及所见所闻出发，以叙事的形式呈现，就像是在跟朋友交谈，让人感到亲切，学生学起来有味道，自然就理解了相关概念，同时，结合实例让学生思考，有图表、图形让学生观察，自觉对比，这样的教学就有趣多了[3].