华南区域模式在湖南省的2 m温度预报检验与订正研究
2022-11-24陈静静兰明才周长青
陈 龙,陈静静,兰明才,周长青,付 炜
(1.湖南省气象台,湖南 长沙 410118;2.气象防灾减灾湖南省重点实验室,湖南 长沙 410118;3.湖南省永州市气象局,湖南 永州 425000)
0 引言
随着社会经济的快速发展,政府和公众对气象预报的关心程度日益增强,对气象预报服务的精细化、精准化程度要求不断提高。温度作为气象预报的基本要素,其精细化预报已成为天气预报技术发展研究热点。湖南地形呈向北开口的平原与三面环山的马蹄状特点,天气系统影响复杂,精细化温度预报成为湖南地区天气预报的难点之一。
高分辨率数值预报模式的发展为精细化天气预报提供了丰富的客观产品,但由于大气混沌效应、数值模式初始场误差以及物理过程难以完美体现等问题,数值模式预报存在不可避免的系统性偏差。因此,发展合适的偏差订正技术有助于提高温度预报的精细化、精准化程度。为了减小模式误差,一方面可以通过资料同化改善初始场或改进模式框架[1-6]等途径,提高数值模式预报准确性;另一方面,可以利用客观订正技术[7-11]改进预报偏差,提升模式适用性。
预报检验是数值模式应用与订正的基础。我国学者陆续开展了全球数值模式和区域数值模式温度预报的本地化检验评估工作,各模式呈现出季节、日变化、地域、复杂地形等系统性偏差。全球模式中,ECMWF、GRAPES_GFS和T639温度预报均能较好地反映出温度日变化特征,ECMWF整体表现较好,在中国区域整体预报偏低,整点温度、高低温预报存在明显的季节和地域差异,东部预报效果优于西部,低温预报效果明显优于高温预报[12-14]。近几年,随着预报业务对精细化程度要求的提高,国内自主研发的中尺度区域模式快速发展,由于模式框架、同化系统和空间分辨率等不尽相同,对温度预报表现各异[15-19]。各区域模式也能较好地表现温度日变化与季节特征,GRAPES_Meso低温预报优于高温预报,偏差表现呈东低西高[15];针对短临预报的GRAPES_RAFS温度预报高原和复杂地形区域呈系统性偏低,华北、南疆地区预报偏高[16];华中、华南区域模式温度预报效果优于GRAPES,华中区域模式预报暖季优于冷季,华南区域模式则表现出高温预报阶段偏差明显,夏季预报偏低,冬季偏高[17-20]。
发展模式预报客观订正技术是解决模式系统性偏差的有效途径之一。现有研究多基于单模式或多模式,利用等权或非等权的误差订正方法改进温度预报。一元线性回归、多元线性回归、消除偏差集合平均、MOS、卡尔曼滤波和超级集合预报等方法均能有效减小温度多时效预报偏差[21-26]。
湖南现有温度客观预报仅基于温度预报因子订正,未考虑多因子对温度的影响,因此,利用华南区域模式的更新快、精度高等特点,本文在华南区域模式2 m温度预报偏差分析的基础上,建立基于多因子影响的逐步回归订正模型,旨在提高2 m温度预报准确性,为预报员提供更为精准的温度预报参考依据。
1 资料与方法
1.1 资料说明
本文所用资料包括湖南97个国家站逐小时2 m温度实况数据,华南区域模式(CMA-GD)各层预报产品和根据模式计算得到的温度平流、涡度、散度预报产品,总计165个预报因子,空间分辨率3 km×3 km,反距离权重插值到湖南97个站点。模式预报与实况数据选取时段为2019年8月—2020年7月,模式起报时间为00、12时(世界时,下同),预报时效为0~84 h,其中2、8月为检验数据集,训练数据集根据订正思路分别选取①全年、②冬半年(11月—次年4月)、③夏半年(5—10月)。根据业务实际需求,建模预报时间为起报时间往后的13~84 h预报(为方便对结果进行分析,下文以1~72 h代称)。
1.2 逐步回归法
综合考虑多因子对2 m温度的影响,通过对165个因子与实况2 m温度的相关分析进行初筛,各站因子初筛标准为通过0.05显著性水平检验,再选取与20%以上站点相关性均较好的25个因子作为变量引入逐步回归方程,初选因子见表1。

表1 华南区域模式预报初选因子
逐站建立模型,引入多个变量构建回归模型并进行检验,删除不显著变量,最终得到包含显著变量的逐步回归方程。逐步回归方程如下:
(1)
式中,y1,y2,…,yn为2 m温度因变量,β0,β1,…,βp为p+1个待估计系数,x11,x12,…,xnp是n次回归引入的p个预报因子,设e1,e2,…,en是n个相互独立的且遵从同一正态分布N(0,σ)的随机变量。
1.3 检验方法
以平均误差、平均绝对误差、均方根误差和预报准确率为指标,对比模式订正预报、模式预报与实况结果,讨论华南2 m温度预报与订正效果。
预报准确率即中国气象局对各省市气象部门的考核标准,反映预报相对于实况的预报效果,详见公式(2)。
(2)
式中,N为预报个数,当预报与实况之差的绝对值≤2 ℃时,表示预报正确,NA为预报正确个数。当CR为1时,即准确率达到100%。
2 结果分析
2.1 2 m温度预报检验
分析实况与华南区域模式2 m温度预报,大部分站点的相关系数大于0.9,以龙山站为例(图略),每日00时起报的逐小时温度预报与实况的相关系数达0.942,平均绝对误差为2.153 ℃,均方根误差为2.809 ℃,华南区域模式与实况变化趋势基本一致,能较好地反映2 m温度的日变化特征。
分析华南区域模式00、12时起报的1~72 h逐24 h 2 m温度预报,97站的平均准确率分别为0.58、0.42,均方根误差分别为2.84 ℃、4.1 ℃,00时起报的2 m温度预报明显优于12时起报的。00、12时起报的1~72 h预报中, 24 h预报准确率最高,分别为0.63、0.44,均方根误差最小,为2.5 ℃、3.99 ℃,预报效果明显优于48 h、72 h预报。
2.1.1 逐时预报检验 通过分析华南区域模式00时起报的1~72 h逐时2 m温度预报,探讨华南区域模式逐时2 m温度预报偏差。从图1a、b来看,准确率与均方根误差均呈明显日变化,白天12~21 h、36~45 h、60~69 h(即北京时的08—17时)时段,准确率明显下降,均方根误差明显上升,正午时段预报准确率达到最低、均方根误差达到最大;夜间,即每日09时—次日00时,准确率均在上升后维持在1 d中的最高水平,均方根误差保持最小。从平均误差与平均绝对误差来看(图1c、d),华南区域模式白天时段误差更大,以负偏差为主,夜间时段存在正偏差,在日出和日落时分,误差达到最大。随着预报时效的延长,模式预报呈准确率下降、误差增大趋势。
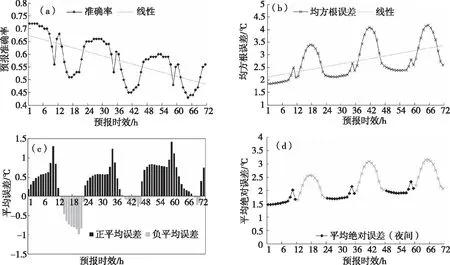
图1 湖南地区00时起报1~72 h逐时2 m温度预报准确率(a)、均方根误差(b)、平均误差(c)、平均绝对误差(d)
2.1.2 1~24 h逐月检验 分析华南区域模式00、12时起报的1~24 h逐月2 m温度预报(图2),探讨华南区域模式2 m温度预报月、季偏差。00时起报的2 m温度预报中,8月平均准确率最低、均方根误差最大,分别为0.5、2.76 ℃;1月准确率最高、均方根误差最小,分别为0.71、2.14 ℃;夏半年(5—10月)整体准确率明显低于冬半年(11月—次年4月),均方根误差也偏大。12时起报的2 m温度预报在8月准确率最低、1月准确率最高,除1月外,冬半年均方根误差较高。00时起报的2 m温度预报效果明显优于12时起报。

图2 湖南地区00时、12时起报1~24 h 2 m温度预报逐月均方根误差(a)及准确率(b)
2.1.3 2 m温度预报偏差的空间分布 通过分析华南区域模式00、12时起报的1~72 h 2 m温度预报平均准确率、均方根误差的空间分布,探讨华南区域模式在湖南不同地区的预报效果。从均方根误差来看(图3a、b),00时起报的2 m温度预报整体偏差较小,均方根误差大部分站点在2~3 ℃,南岳站及个别海拔较高站点、湖区站点偏差偏大;12时起报的2 m温度预报整体偏差较大,均方根误差集中在4~5 ℃,湘东、湘西南部分站点在3~4 ℃。从准确率来看(图3c、d),00时起报的2 m温度预报准确率大部站点在0.5以上,海拔稍高地区预报优于平原与谷地;12时起报的2 m温度预报大部站点准确率在0.5以下,湘东北部分站点仅有0.3~0.4。受地形与模式系统性偏差影响,华南区域模式对湖南不同区域2 m温度预报效果不同,湘西整体优于湘东。对大部分站点,00时起报的2 m温度预报效果明显优于12时起报。
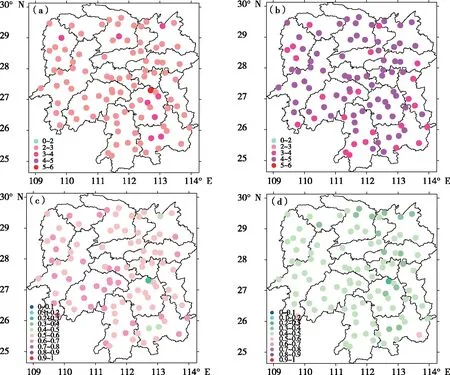
图3 湖南地区00、12时起报1~72 h 2 m温度预报平均均方根误差(a、b,单位:℃)及准确率(c、d)空间分布
2.2 逐步回归订正检验
2.2.1 不同起报时次的温度订正 分别对1~72 h逐时包含00、12时起报的模式预报数据集与00时、12时起报的模式预报数据建立逐步回归模型,结果显示(图4),分起报时次的订正结果相较于不分起报时次建模的订正结果平均绝对误差、均方根误差更小,准确率也略优,两者较直接模式预报而言,均有正技巧。分与不分起报时次建模订正的2 m温度,00时起报的订正结果均优于12时起报,两者均优于模式预报。
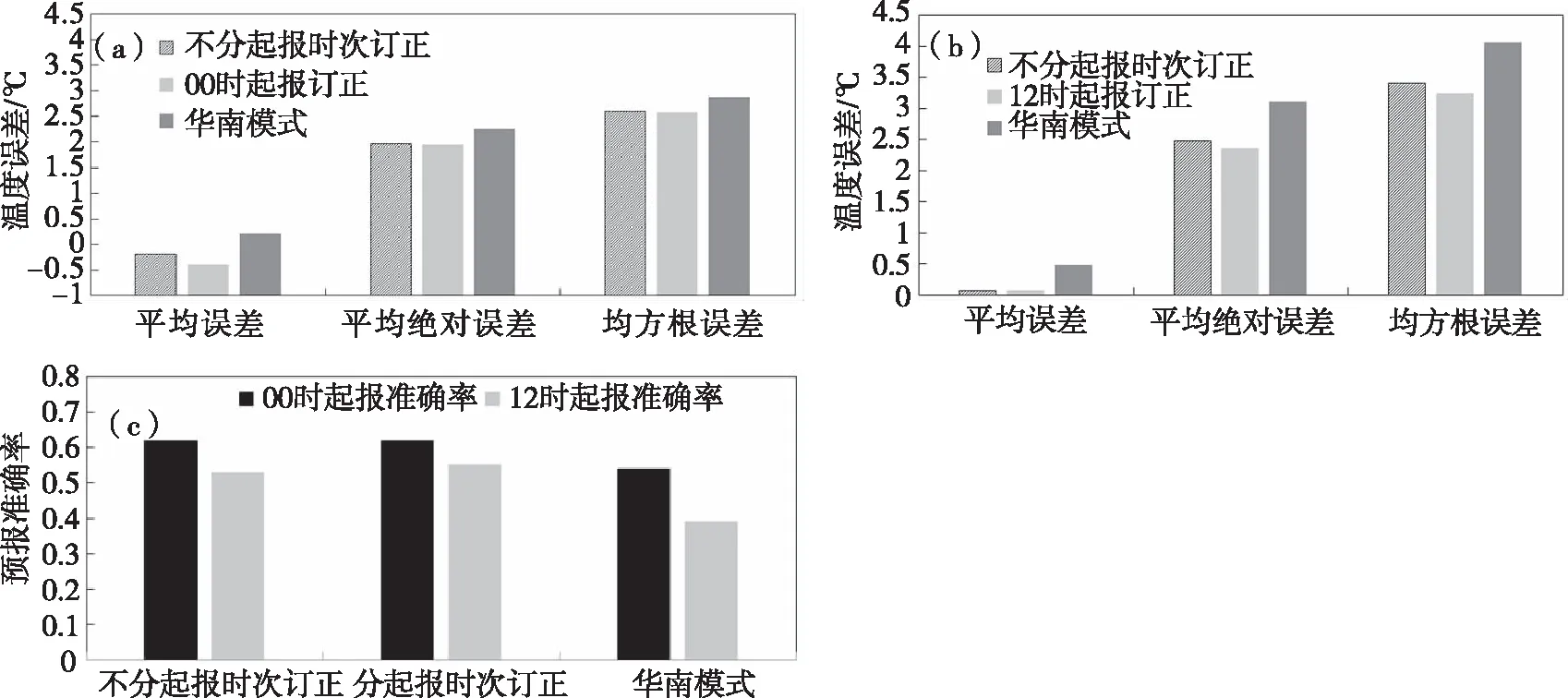
图4 湖南地区分与不分起报时次2 m温度订正预报平均误差、平均绝对误差、均方根误差(a)(b) (单位:℃)及准确率(c)
2.2.2 不同时段的温度订正 以不同起报时次建模为基础,将1~72 h作为整体数据集与分别包含1~24 h、25~48 h与49~72 h的数据集建立逐步回归模型。结果显示(表2、图5),以1~72 h为整体的建模订正结果,1~24 h的订正准确率优于25~48 h、49~72 h,随着预报时效延长,订正效果下降,各时段00时起报订正结果准确率均优于12时起报,基于逐步回归的订正产品优于模式预报。00、12时起报的分时段建模订正结果准确率相对于不分时段的订正结果无明显变化,误差略有增加。
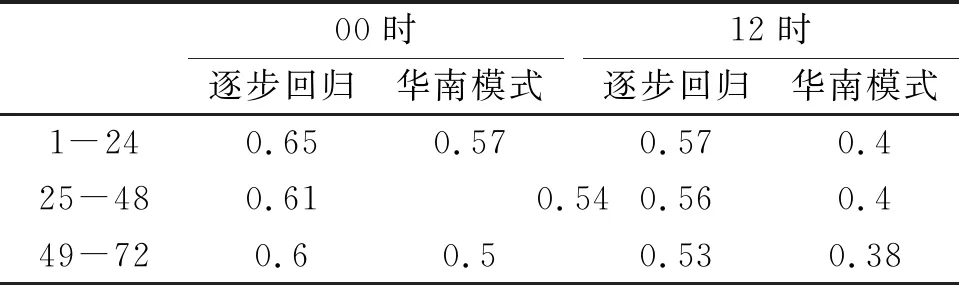
表2 00时、12时分起报时次不分时段的2 m温度订正预报准确率

图5 12时起报分时段的2 m温度订正预报准确率(a)与均方根误差(b)
2.2.3 不同季节的温度订正 以分起报时次、1~72 h作为整体建模为基础,将1—11月作为整体数据集与分别以冬半年11月—次年4月、夏半年5—10月的数据集建立逐步回归模型。结果显示(表3),分季节的5—10月建模、11月—次年4月建模的订正结果准确率均高于不分季节建模的订正结果,均方根误差也有明显下降,8月订正效果更为明显。基于逐步回归的订正产品相对于模式预报均呈正技巧。

表3 分与不分季节的2 m温度订正预报准确率与均方根误差(单位:℃)
2.2.4 分起报时次和季节订正结果的空间分布 根据前文分类建模结果分析,以分起报时次、不分时段、分季节建立数据集,对湖南97个国家站分别建立逐步回归模型,以2、8月作为检验时段,通过分析订正结果对模式的准确率差值(技巧),探讨基于逐步回归的华南区域模式2 m温度订正产品的空间订正效果。结果显示(图6),00时, 2月,山区有明显的正技巧,平原地区大部站点订正效果略差; 8月,平原与山区具有正技巧,平原地区订正效果更明显。12时,2、8月均有正技巧,8月订正效果显著,平原订正效果优于山区。

图6 分季节2 m温度订正预报与模式预报准确率差值空间分布(00时起报2月(a)、8月(b),12时起报2月(c)、8月(d))
3 结论
①华南区域模式与实况变化趋势基本一致,能较好地反映2 m温度的日变化特征。逐时2 m温度预报误差呈明显日变化,白天误差增大、准确率下降,夜间预报效果相对较好;温度预报在日出和日落时段负偏差最大;模式预报夏半年准确率明显低于冬半年;随着预报时效的延长,模式对2 m温度预报能力下降。受模式系统性偏差影响,华南区域模式对湖南不同区域2 m温度预报效果不同,湘西整体优于湘东,海拔稍高地区预报优于平原与谷地。00时起报的2 m温度预报效果优于12时起报的。
②基于逐步回归对华南区域模式2 m温度预报在不同起报时次、不同时段、不同季节建立的模型,其结果相对于直接模式预报均有正技巧,其中,分起报时次订正结果更优;分时段订正结果无明显优势;分季节订正结果明显好于全年订正结果。分起报时次、不分时段、分季节建立的逐步回归订正模型相对模式预报有较大的提升,不同季节订正效果不同。
③采用逐步回归模型订正的2 m温度客观预报在空间上技巧表现存在差异。00时,2月山区有明显的正技巧,平原地区订正效果略差;12时,2、8月均有正技巧,平原订正效果优于山区。
