基于数学历史名题的解题教学
——以“不可及物的测量问题”为例
2022-11-24张维忠浙江师范大学教师教育学院321004
侯 甜 张维忠 (浙江师范大学教师教育学院 321004)
解题教学是数学教学的重要部分,学生在学会解题的过程中发展了思维能力,提高了数学核心素养[1].目前的解题教学存在一些问题:学生的学习兴趣被大量解题冲淡;注重解题技巧,忽视思维发展;题目远离教材,出现难题怪题;课堂缺乏文化气息……数学历史名题作为数学史的重要内容,对数学发展、数学教学和数学应用有着推动作用,题中真实的问题情境、实质性的数学思想方法、丰富的人文背景等对于教学都有重要意义.[2]鉴于此,本文以“不可及物的测量问题”为例,选取《海岛算经》中的数学历史名题进行教学设计,探索数学历史名题如何助推解题教学.
1 数学解题教学存在的问题
美国数学家哈尔莫斯说:“数学的真正组成部分应该是问题和解,解题才是数学的心脏.”解题教学是培养学生发现和提出问题、分析和解决问题能力,拓展学生数学思维,发展数学核心素养的重要手段.但目前的解题教学还存在一些问题.为了更好地改进教学,教师应当正确认识问题,并提出解决策略.
第一,学生的学习兴趣被大量解题冲淡.大多数解题教学都是通过枯燥的题目训练来达到让学生学会解题的教学目的,这种缺乏创新的教学方法不能满足学生的心理需求,大量的题目将数学学科的枯燥性放大,学生的学习兴趣、探索热情被不断冲淡[3].
第二,注重解题技巧,忽视思维发展.解题教学中通常都充斥着各种类型的题目,教师注重题型分类和变式练习,在对例题进行分类讲解后,归纳每种题型的解题方法,要求学生利用技巧求解问题,并做大量练习.这种教学方法虽然可以让学生快速掌握一些问题的求解方法,收获短期效益,但长远来看并不利于学生的思维发展,学生在学习过程中没有进行主动的思考探索,将解题视为根据题型套技巧的活动[4].
第三,题目远离教材,出现难题怪题.重视题型归类和技巧训练的解题教学,往往从各式各类的题目出发展开教学,欠缺对学生知识建构的考虑,出现远离教材的现象,一些难题、怪题还会作为创新点出现.
第四,课堂缺乏文化气息.尽管当前课程改革多次强调数学课堂文化,但解题教学中的文化气息仍较为缺乏.教学在大量刷题中追求标准答案,重视从问题背景中提炼关键信息,忽视问题的文化韵味,多为达到功利性、应试性目的[5].
2 数学历史名题助推解题教学
在数学历史发展的长河中,产生了很多对数学史有较大影响,对数学发展、数学应用和数学教学有重要推动作用的数学历史名题.历史名题通常从现实问题中提出,问题背景真实自然,能很好地体现所涉及数学内容的实践价值,同时对于学生来说,真实的情境不仅利于激发学习兴趣还利于知识理解.问题中蕴含的数学思想方法,对于学生的思维发展有重要促进作用,学生收获的不仅是解某一类数学问题的方法,更是数学地看待问题的思维.教师还可通过数学历史名题中丰富的人文背景对学生进行文化熏陶、情感教育,落实“立德树人”的教育目标.如此,数学历史名题可以从激发兴趣、拓展思维、强化应用、文化育人四方面助推解题教学,解决现存问题,改善现有教学.
融入历史名题,激发学习兴趣.巧妙运用数学历史名题真实自然的问题背景,为原本枯燥的解题过程增添活力.一方面,可以将历史名题作为教学引入,用耐人寻味的问题开启课堂,将学生的注意力吸引到如何利用所学解决问题上.另一方面,由于学生的兴趣容易被大量枯燥的题目冲淡,因此在对例题进行分类讲解时,可以将历史名题作为例题或者将历史名题中的情境改编到例题中,激发学生学习兴趣.
探究名题解法,拓展数学思维.在讲解名题时注重多种解法的探究,打破固有思维.数学发展的不同阶段对于名题的求解方法不同,这些方法往往可以体现当时数学发展的特点,蕴含着重要的数学思想方法,因此教师可以从已有的解题角度出发,引导学生探究.在引导探究的过程中,更重要的是让学生感受解决数学问题的多种视角,培养发散思维[6].
联系教材实际,强化知识应用.新一轮课程改革中强调数学文化融入教学,多版初中教科书都分布有数学历史名题,中考试题中数学历史名题的出现频次也呈上升趋势.解题教学应与教材实际和学生已有的知识体系紧密相连[7].为此,教师既可以充分挖掘教材中已有的或隐含的数学历史名题来开启教学,也可以选取中高考中包含历史名题的试题进行应用链接,改善解题教学中题目远离教材、偏难偏怪的现象.
渗透文化背景,进行情感熏陶.数学历史名题作为数学发展长河中留存下来的经典问题,是数学世界的璀璨明珠,其深厚的人文背景是对学生进行情感教育的良好素材.教师在应用历史名题前,应充分了解其时代背景、相关数学家、发展历史等,让学生在认识名题的过程中获得良好的情感体验,如感受我国古代数学的博大精深,增长民族自信,体会数学家严谨的治学态度和锲而不舍的探索精神,改变错误的学习观念等.
3 相关教学设计
解双直角三角形是初中数学的重点内容,《义务教育数学课程标准(2022年版)》中强调:“知道直角三角形的边角关系,理解锐角三角函数,能用锐角三角函数解决简单的实际问题.”[8]不可及物的测量问题是解双直角三角形的经典题型,在中考中多次出现.《海岛算经》是我国数学家刘徽所著的中国最早运用几何理论解决各种测量难题的数学专著,主要解释“重差术”问题,即不可及物高度和距离的测量问题,书中的数学问题包含多种真实情境,蕴含着重要的数学思想方法,是“不可及物测量问题”教学的优秀素材.
3.1 名题引入,激起兴趣
魏晋时期伟大的数学家刘徽在其著作《海岛算经》中留下了九道经典的测量名题,其中第1题为“望海岛”问题——在地面立前后两根表来测量远方的一处海岛,两表高均为3丈(5步),相距1 000步,先从前表出发后退123步观察海岛顶端,再从后表后退127步观察海岛顶端.问:海岛高为多少?海岛与前表之间的距离为多少?(注:古代1丈=10尺,1步=6尺)
设计意图此题源于现实生活,是有关不可及物测量问题的数学历史名题,出自我国古代数学家刘徽的著作《海岛算经》,选取此种与教学内容紧密相连的历史名题引出教学,激发学生的学习兴趣.
3.2 一题多探,发展思维

探究1 预设学生最先想到的解题思路是利用相似三角形的判定及性质进行证明,引导学生应用平面几何的知识证明岛高和岛去表的测量公式.
探究2 “望海岛”问题本质上是解双直角三角形.在进行本课之前,学生已经学习了利用锐角三角函数解直角三角形,故此引导学生利用锐角三角函数的知识证明岛高和岛去表的测量公式.
探究3 《海岛算经》是刘徽在魏晋时期所著,根据当时的数学水平,三角学还未出现,现代数学家吴文俊认为可以采用“出入相补”原理进行证明,赵爽在《周髀算经》中遗留的“日高图”中也蕴含此思想.引导学生思考如何利用面积思想和“出入相补”原理证明“望海岛”问题.
设计意图引导学生探究名题的多种解法,从教解题到教思维,在解题教学中进行思维教学,帮助学生在问题思考过程中认识问题和解法的本质,提升思维能力,发展核心素养[3].探究1中的“比例法”涉及初中平面几何知识,利用相似三角形对应边成比例的性质定理进行求解,是初中生最容易理解和掌握的方法.探究2的“三角法”体现了锐角三角函数在解直角三角形中的重要作用,“望海岛”问题本质上是不可及物高度和距离的测量问题,此类问题正是解直角三角形的经典题型,三角法是最为普遍的解题方法.探究3中的“面积法”所用到的“出入相补”原理是我国古代数学的智慧结晶,此原理可以应用于勾股定理、多边形面积公式、等差数列求和等多个教学之中,引导学生利用此原理思考“望海岛”问题,既是对学生数学思维的培养,也能通过体会古代数学的博大精深激发爱国热情.三次解题探究,让学生掌握了多种求解不可及物测量问题的方法,体会从几何、函数、代数等方面进行问题探究的发散思维.
3.3 变式检测,合作探究
变式1 改编自《海岛算经》中的“登山望津”问题:如图1,今有登山望津(AB),津在山南.偃矩山上,令勾(CD)高一丈二尺,从勾端(C)斜望津南岸(A),入下股(DE)二丈三尺一寸;又望津北岸(B),入前望股里一丈八寸(EF),津南岸去山脚(G)五丈二尺(AG).问津广(AB)几何?
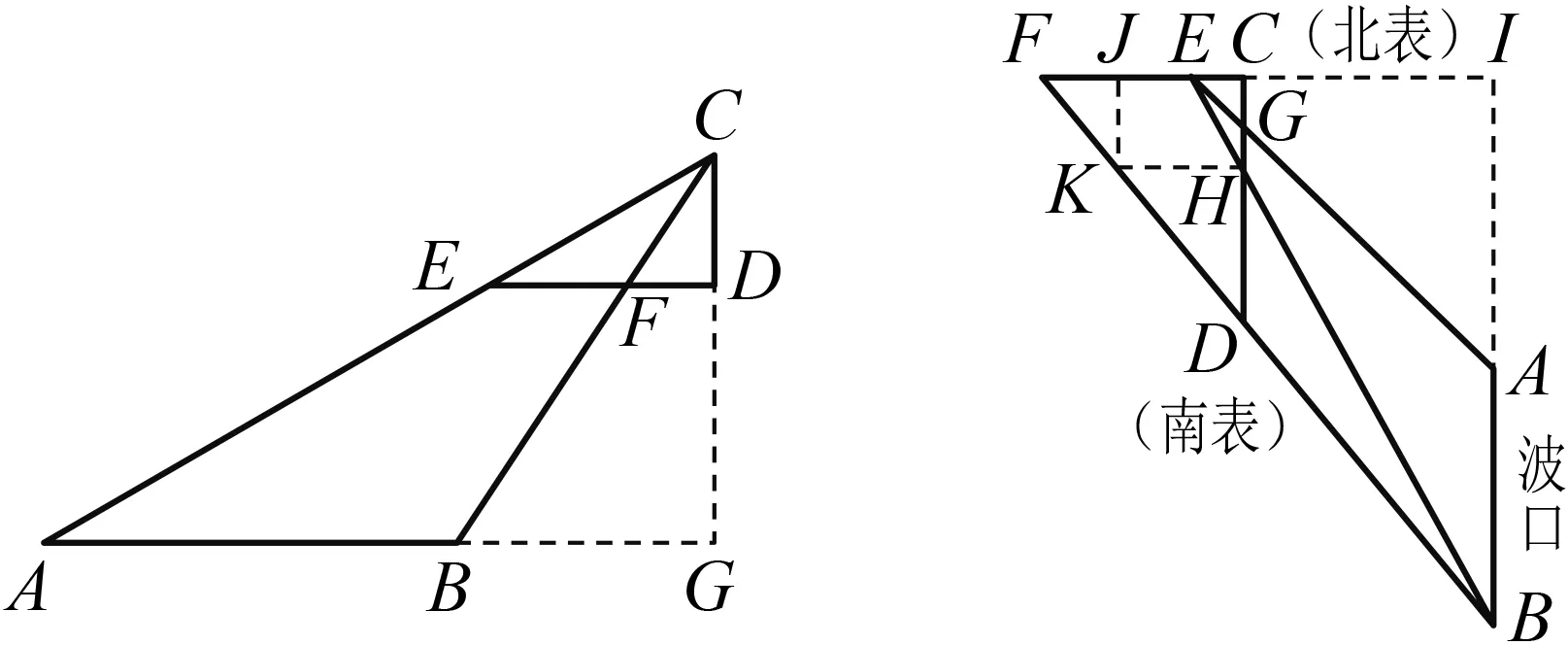
图1 图2
变式2 摘自《海岛算经》中的“望波口”问题:如图2,今有东南望波口(AB),立两表(C,D)南北相去九丈(CD),以索薄地连之.当北表之西却行去表六丈(CE),薄地(E)遥望波口南岸(B),入索北端(H)四丈二寸(CH);以望北岸(A),入前所望表里(G)一丈二尺(GH).又却后行去表十三丈五尺(CF),薄地(F)遥望波口南岸(B),与南表参合.问波口(AB)广几何?
教学活动:以小组为单位进行讨论,探究“望海岛”问题的三种解题方法能否求解上述两个变式,讨论“登山望津”问题、“望波口”问题与“望海岛”问题有哪些不同.
设计意图《海岛算经》中包括不可及物测量问题的多种情境,选取其中两道符合初中生认知发展水平的名题作为变式探究,并以小组为单位用3.2节中的三种解题方法求解变式问题.教学引入的“望海岛”问题是在与不可及物底端同一平面上的两个点,对物体的顶端进行两次观测;变式1中改编的“登山望津”问题是在与观测物不处于同一平面的一个点,对不可及物的两个端点分别进行观测;变式2中的“望波口”问题是在两个点对不可及物进行多次观测.通过变式问题进一步巩固解法,在探究解法是否适用的过程中进一步体会数形结合、等量代换等数学思想,同时将改编后的历史名题作为变式,真实生动的情境能为解题增添活力,调动学生探究的积极性.
3.4 实战演练,深化理解
题1(浙教版)广场上空有一个气球A,地面上点B,C,D在一条直线上,BC=20 m.在点B,C分别测得气球A的仰角∠ABD为45°,∠ACD为56°.求气球A离地面的高度AD(精确到0.1 m).
题2(2018·宁波中考)如图3,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45°和30°.若飞机离地高度CH为1 200 m,且点H,A,B在同一水平直线上,则这条江的宽度AB为多少m?(结果保留根号)
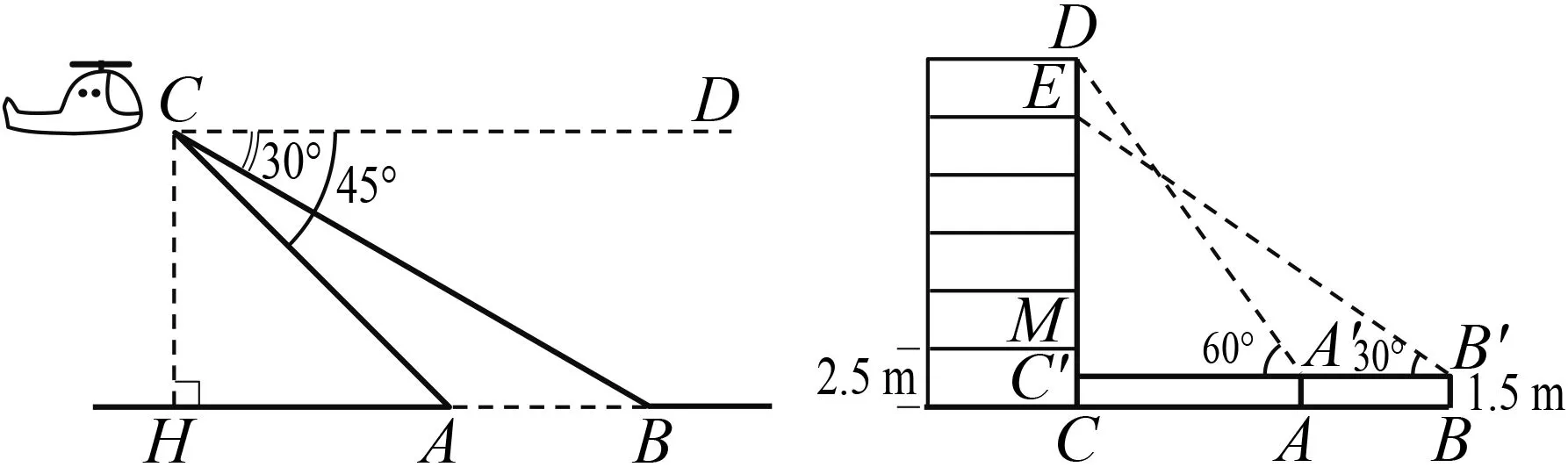
图3 图4
设计意图不可及物测量问题在课后习题中常有出现,在中考中出现的频率也很高,2020年河南省、2019年天津市、2018年衢州市、2014年绍兴市等地的中考卷中都有类似考题.选用教材中的课后习题和中考真题作为应用链接,加强解题与教材之间的联系,一方面能帮助学生巩固所学,在解题时回顾教材,梳理知识,进一步完善知识网络,同时在练习中考真题时能更好地把握考点,大多数中考真题的条件简单,难度较低,利用锐角三角函数求解最为快捷有效;另一方面,学生在解题过程中可以体会知识的实际应用,感受丰富的文化韵味,保持学习的积极性.
4 进一步的思考
将《海岛算经》中的历史名题融入“不可及物测量问题”的解题教学,真实有趣的情境为课堂增添了活力,学生在探究名题解法的过程中掌握了求解此类问题的通法,体会到数形结合、等量代换等数学思想的博大精深,最后练习相关课后习题和中考真题进行知识巩固,同时教学还利用历史名题的时代背景、相关人物、发展历史等对学生进行文化教育.
4.1 历史名题合理融入教学
融入教学的历史名题应与教学存在紧密联系,并符合学生的认知水平.“望海岛”问题是“不可及物测量问题”的经典题型,教学中探究的“比例法”“三角法”“面积法”都能被学生理解掌握.通常来说,数学历史名题的语言表达较为晦涩难懂,会给学生带来一定的认知负担,教师在教学过程中可以对题目进行合理改编或增加注释、图示,同时注重引导学生从问题中抽象出数学模型.如本教学案例中的变式2是对《海岛算经》中“登山望津”问题进行的简化改编,并配以图示呈现给学生,减少学生的认知负担.数学历史名题在经过科学合理的组织之后,能更好地融入并促进教学.
4.2 多种解法拓展数学思维
解题教学不能只关注教解题,还应着眼于学生的思维发展,让学生学解题.为使学生在面对问题时积极运用已有知识经验多角度思考,教师可以通过引导学生一题多解来进行思维培养.如在本教学案例中,共引导学生进行了三次解法探究:第一种应用平面几何知识的“比例法”是史料中的解法,该方法最易于理解;第二种运用锐角三角函数的“三角法”是初中阶段解直角三角形的常用办法,适用范围最广;第三种基于“出入相补”原理的“面积法”是我国古代数学中转化思想的重要体现,虽然此方法在不可及物测量问题中适用范围较窄,但可以让学生体会我国古代数学智慧,增长民族自信,获得良好的情感体验.
4.3 回归教材强化知识应用
解题教学最终要落实到学生的实际应用中,所教内容回归教材、链接考试,有助于学生进一步作解题反思,巩固所学.本案例中将浙教版教材中的课后习题和各地中考真题作为练习题目,一方面检测教学效果,补充教学不足;另一方面引导学生在练习的过程中梳理知识点、把握考点,深化知识理解,强化知识应用.
