韦达定理:历史、教育价值及启示
2022-11-24黄贤明江苏省苏州高新区景山实验初级中学校215129
黄贤明 (江苏省苏州高新区景山实验初级中学校 215129)
韦达定理是一元n次方程根与系数关系的定理,本文主要讨论一元二次方程的情况.在现行教材中,韦达定理一般编排在一元二次方程的解法之后,在中学阶段具有较为广泛的应用价值.《义务教育数学课程标准(2011年版)》中韦达定理为选学内容,《义务教育数学课程标准(2022年版)》(下称新课标)则将韦达定理重设为考试内容,说明韦达定理的教育价值不容忽视.研究韦达定理的起源与发展,不难发现其蕴藏着深厚的历史底蕴,是HPM教学研究的重要素材;同时韦达定理作为数学定理,在其发现、探索、证明、应用等环节中也涉及到数学抽象、逻辑推理等素养的 培养.因此,本文从历史和教育价值两个方面透析了韦达定理,以期提出韦达定理教学的建议与启示.
1 韦达定理的历史
1.1 韦达定理的起源与发展
韦达定理从起源、发现、完善、证明到推广历经了数百年,历史上对于方程的根与系数关系的探索可以追溯到16世纪,意大利数学家卡丹 (G.Cardano,1501—1576)、法国数学家佩勒蒂耶(J.Peletier,1517—1582)、意大利数学家邦贝利(R.Bombelli,1526—1572)都发现了方程的根与系数的规律[1].1615年,法国数学家韦达(F.Vieta,1540—1603)在《方程的理解与修正》一书中给出了形如-x2+px=q(p,q>0)的方程的两根之和为p,两根之积为q,但韦达并没有考虑重根和负根的情况.1629年荷兰数学家吉拉尔(A.Girard,1595—1632)在《代数新发明》中讨论了一般n次方程的根与系数关系,并将根推广到负数、虚数,且发现了方程根的“幂和公式”.直到18世纪,瑞士数学家欧拉(L.Euler,1707—1783)、法国数学家拉克洛瓦(S.F.Lacroix,1765—1843)等人才给出了韦达定理的严格证明[2].在19世纪苏格兰数学家华里斯(W.Wallace,1768—1842)利用韦达定理得到一元二次方程的求根公式[3].由韦达定理的历史可以看出,求根公式的出现远晚于韦达定理,并非教科书所编排的顺序,其次早期韦达定理考虑的是二次项系数为1的一元二次方程.
1.2 韦达定理的证明
纵观韦达定理的历史发展,许多数学家都为定理的证明作出了贡献,并且他们的证明思想都围绕着设而不求的数学思想.
(1)韦达代入相减法.
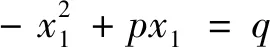
在证明中,韦达并没有考虑到重根的情况,但他是最早以定理的形式探究方程的根与系数关系的数学家,并且在他的证明过程中也蕴藏着设而不求的数学思想与代入相减的数学方法.
(2)吉拉尔代入相减法.

数学家吉拉尔的证明是站在韦达的“肩膀”上,证明思想与方法都类似于韦达的证明.但该证明弥补了对重根情况的讨论,且韦达定理的形式也与如今教材中所呈现的相同.
(3)欧拉因式分解法.
设方程x2+px+q=0的两根为x1和x2,则原方程可化为(x-x1)(x-x2)=0,即x2+px+q=x2-(x1+x2)x+x1x2,比较系数,得x1+x2=-p,x1x2=q.
欧拉的证明也是采用设而不求的数学思想,但与韦达证明的不同就是利用所设两根对方程进行因式分解,比较系数得到定理,这也是人教版教材中所采用的证明方法.
(4)拉克洛瓦“新证法”.
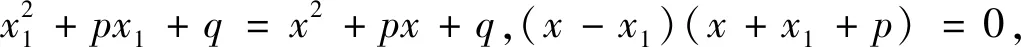
拉克洛瓦在证明中没有将两根全部设出,通过只设一根的方式,让另一根通过运算推理获得.
2 韦达定理的教育价值
2.1 串联中学解题的重要法宝
在初中阶段,韦达定理并没有得到较为深入的探究与应用,其主要用于解决判断方程根的符号这类问题.此外,从课外拓展的视角下,韦达定理还可以用于求解特殊的方程组、分式方程、不定方程等问题[4].在高中阶段,韦达定理在解析几何的求解中较为常见,尤其是涉及直线与圆锥曲线的关系问题,借助韦达定理可以巧妙地设而不求、简化运算.在韦达定理的证明方法中,利用因式分解法可以将一元二次方程推广到一元n次方程,走向定理的一般化.因此,韦达定理在中学数学解题中,其内容、思想、方法都是学生的重要法宝.
2.2 发展核心素养的重要载体
新课改以来,数学核心素养与数学思想方法受到一线教师的重点关注.韦达定理作为数学定理,其本身就具备较强的严谨性和逻辑性.在教学实践中,不同的教学设计下,韦达定理能够达到不同的培养目标.以苏科版教材的设计为例,在观察、比较具体方程及其根的关系的活动中,有利于培养学生数学抽象素养与合情推理能力;在使用求根公式证明定理环节,有利于培养学生数学运算和逻辑推理素养.除了教材的设计,教师还能从不同的视角对韦达定理的教学进行再设计.例如,基于5E教学模式并融合了因式分解法证明韦达定理、利用韦达定理证明求根公式等活动,让逻辑推理素养串联起整个课堂[5].再如,在发现规律环节中设计“数学趣味游戏”,让学生根据已给方程的根构造一元二次方程,并得出猜想,该环节侧重于学生数学抽象素养的发展,同时也涉及归纳推理、逆向思维等能力培养[6].
2.3 浸润德育美育的重要素材
在韦达定理发展的历史长河中,一批批执着追求真理的数学家们前赴后继,他们的故事、生平与成就中蕴含的理想信念与精神品质汇聚成庄重、严肃、令人敬仰的数学精神.教学中将数学史与数学精神渗透在定理的发现中,使其相互映照,让学生在定理的学习中感悟数学精神、丰富历史文化底蕴,并将精神融入学习生活中,指导学生未来的发展,达到数学史的“德育之效”.
此外,数学美是构成数学文化的重要内容,其实质在于理性精神和结构美.从价值追求上,韦达定理引导人们追求尽善尽美的理性精神;从表现形式上,韦达定理既包含着和谐美,也包含着简洁美.和谐美体现于对称式x+y和xy具有简单和谐的对称内涵[7].简洁美在于复杂的一元二次方程两根之和与两根之积仅用两个系数的比值就能简洁地表示出来.
3 启示
3.1 对教师观念的启示
教师是教学的组织者,教师对待韦达定理的教学态度决定了其教育价值的发挥程度.在新课标颁布之前,有些教师就认为:韦达定理是选学内容,考试不作要求,就可以跳过该内容的教学,或让学生自主阅读教材就行.若直接“遗弃”韦达定理,这既不符合数学教学的全面性与基础性,影响学生后续高中阶段的学习,也丧失了培育学生数学核心素养、数学思想方法,渗透德育美育的重要契机,这对学生与教师而言都是一大遗憾.随着新课标的颁布,教师先要摆正意识,正确地对待韦达定理的教学,积极研究教材、研究教学、研究学生,真正做到理解数学、理解教学、理解学生,将韦达定理的教育价值落到实处.
3.2 对教材编写的启示
教材是学生获得数学知识的首要选择,也是教师教学的重要参考.不同的教材对于韦达定理的编写也有所不同,表1从定理发现、定理证明与例题内容三个方面比较了四个版本教材中对于韦达定理内容的编排与设计.
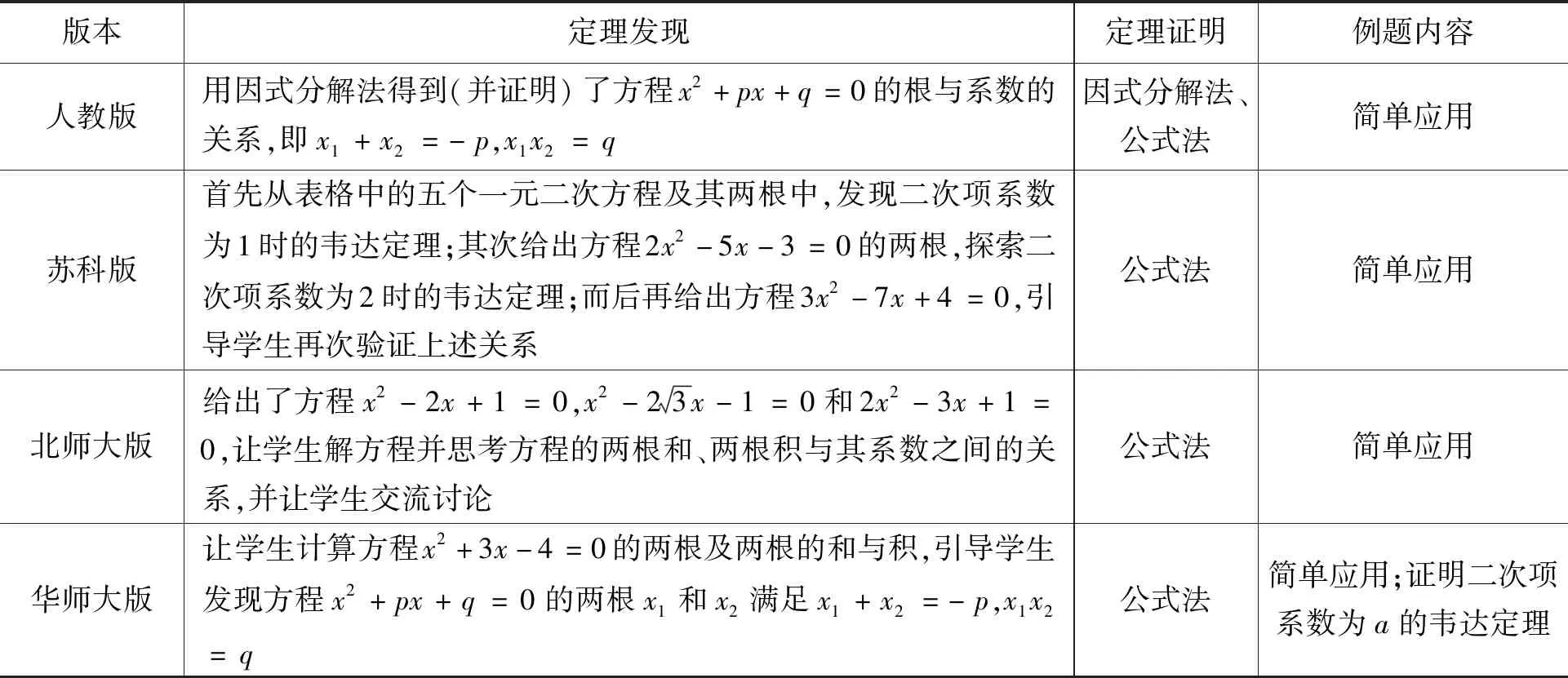
表1 四个版本教材中对于韦达定理内容的编排与设计
就定理发现而言,人教版从因式分解法出发,以逻辑推理(理性)视角发现定理,其他三个版本均从具体的方程出发,以数学猜想(感性)视角发现定理.就定理的证明而言,主要利用公式法证明,
其优点是贴合学生近期学习的内容,更方便、也更容易想到.但这种证明方法不符合历史发展规律(先有韦达定理,后有求根公式),并且一元五次及以上的高次方程没有求根公式,该方法是无法推广的;同时,用公式法证明也会让学生产生对韦达定理学习意义的质疑,即:都能求出方程的具体两根了,为何还要探究两根之和与两根之积.就例题内容而言,四版教材选取的例题都较为单一,只围绕韦达定理的简单应用(给出具体的一元二次方程,求出两根和与两根积),没有从定理逆用的角度选择例题.
综上,教材的编写更侧重于对定理本身的发现与探索,而忽略了韦达定理的发展历史.为更好发挥韦达定理的教育价值,教材的编写可以重构韦达定理的发展史,多角度融入韦达定理的不同证明方法,创设求根公式与韦达定理相互验证的环节,并尝试多方面地设置例题、分层次地设计课后练习,让学生从教材中感受到韦达定理的历史底蕴与价值.
3.3 对教学设计的启示
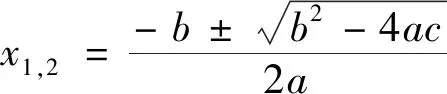

表2 韦达定理教学的五个环节的教学设计
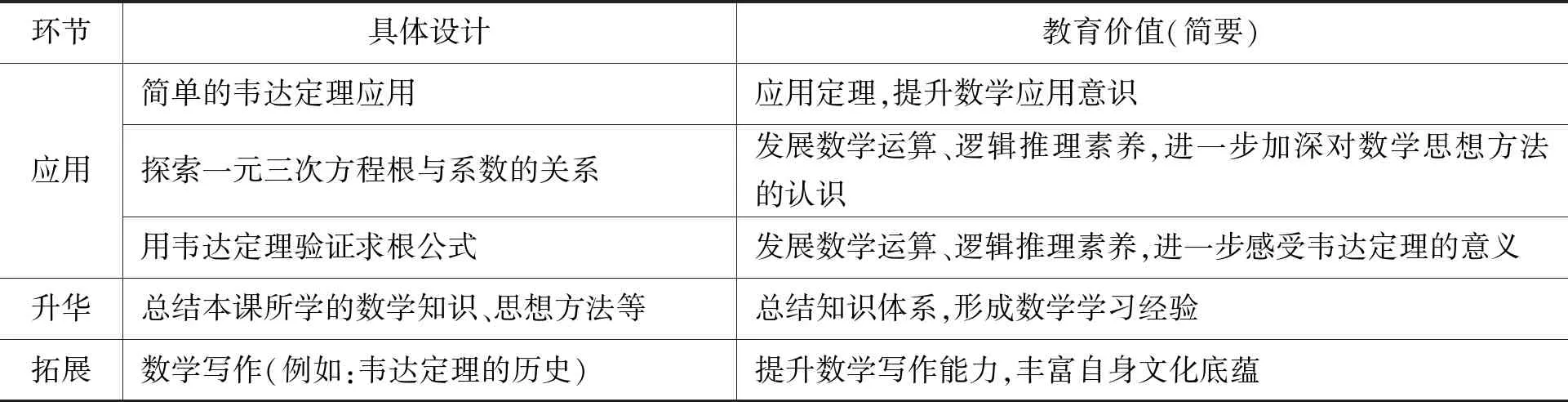
续表
3.4 对作业设计的启示
在“双减”的背景下,作业的设计更要体现诊断、巩固、分析学情等功能,并鼓励以分层、弹性和个性化的形式设计作业.新课标对于韦达定理的教学要求是“了解一元二次方程的根与系数的关系”[9],因此,在韦达定理的作业设计环节更应立足基础、指向文化,使不同层次的学生都得到相应的发展.为协调不同学生的知识基础、思维模式以及学习能力存在的差异,教师可以设置分层、个性化、拓展性作业.例如,A层作业可以选择课本中的习题,进行韦达定理的简单应用,加深对韦达定理的认识;B层作业可以选择韦达定理深入应用或涉及课堂数学思想方法的习题,如求证一元三次方程的韦达定理等等;拓展性作业可以数学写作为载体,涉及韦达定理的历史、探索韦达定理的“美”、韦达定理的证明、韦达定理与求根公式的关系、设而不求的思想及应用等主题,引导学生利用网络资料、图书馆等收集相关材料,形成自己的“一家之言”,同时也激发学生的主观能动性,为学生课外阅读提供指导方向,并促使学生在阅读整理中,提升数学素养、文化素养.
作业的设计与布置延伸了韦达定理的教学,让学生在分层、个性化、拓展性作业中形成对韦达定理的多元化认识,使其教育价值真正在学生发展核心素养的道路上留下深深的“烙印”,成为他们未来数学学习旅途中的“宝藏”.
