合乎逻辑 自然生长
——以“圆的对称性”为例
2022-11-24王新奇江苏省苏州工业园区第一中学215021
王新奇 (江苏省苏州工业园区第一中学 215021)
学生是学习的主体,教师是学习的组织者、引导者和合作者.教师的引导作用表现在教学设计上,在重要环节和学生产生疑惑的环节,通过设计问题引导学生思考,以问题的形式引导学生获取知识,突破教学重点与难点[1].在苏科版教材九年级上册第2章第2节“圆的对称性(第1课时)”的教学过程中,一些教师总觉得这节课的教学效果不好,还有些教师在教学中把结论直接告诉了学生.会出现这些情况的主要原因有以下三个方面:第一,教师在引导学生探索“圆心角、弧、弦”这三个要素之间的数量关系时,由于教学设计不合理,导致课堂上学生的探究活动流于形式;第二,学生在概括探究结论时,由于主体体验不足,忽视了前提条件“在同圆或等圆中”,需要教师提醒或直接告知;第三,教学过程主要以教师讲授为主,学生学得比较被动.2021年4月,在苏州市“名师领航”研修活动中,笔者开设了“圆的对称性(第1课时)”一课,现将教学过程中几个关键环节的教学片段及思考整理成文,与大家探讨交流.
1 教学片段
1.1 感悟“圆的旋转不变性”
教师首先利用PPT展示两个图形:一个等边三角形和一个圆.
师:请观察这两个图形,它们有哪些共同的特点?
生1:这两个图形都是轴对称图形.
师:这两个图形又有哪些区别?
生2:对称轴的数量不一样.等边三角形有三条对称轴,圆有无数条对称轴.
师:圆是轴对称图形,过圆心的任何一条直线都是它的对称轴.因此,圆的轴对称性超越一切平面图形,达到了平面图形轴对称性的最高境界,即轴对称到不能再轴对称了.
生3:等边三角形是旋转对称图形,至少旋转120度才能与自身重合,而圆是中心对称,绕着圆心旋转任意角度都能够与自身重合.
师:圆是中心对称图形,圆的中心对称性同样无与伦比,达到了平面图形中心对称性的最高境界.通过比较我们可以发现,“圆”的特点更加鲜明.现在请大家利用桌上的透明纸制作一个半径为5 cm的圆,然后与同桌合作,把两个圆的圆心叠合在一起,并将其中一个圆转动一个角度,你有什么发现?
生4:转动任意角度都能与自身重合.
师:这就是圆的旋转不变性.
设计意图通过对两个基本图形的观察和交流,引导学生深刻认识圆的两种达到最高境界的对称性,它们是和谐统一的,是圆的同一本质的两种不同表现形式.通过动手操作和体验,进一步感悟“圆的旋转不变性”,同时激活学生原有的知识经验,激发学生参与课堂的热情,也为后续的进一步探索做好铺垫.
1.2 初探“圆心角、弧、弦” 的数量关系
问题如图1,在圆O上任取两点A,B,连结OA,OB,得到圆心角∠AOB,由∠AOB你能想到什么?

图1 图2



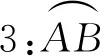
师:如何验证你的发现?


生5:需要再画一个等圆,在等圆中作∠A′O′B′=∠AOB,然后把两个圆的圆心重合在一起,依据“圆的旋转不变性”,转动⊙O′,观察两条弧重合的情况.
师:同桌之间合作一下,验证后请总结你的发现.
生6:在同圆中,相等的圆心角所对的弧相等.
生7:这个结论在等圆中也成立.
师(追问):在探究的过程中,为什么要出现两个圆?
生8:是为了验证等弧.
师:这个结论在“同圆或者等圆中”都成立.
设计意图在“圆心角、弧、弦”三者关系中,“圆心角”与“弧”的对应关系是最直观的.因此,把研究“圆心角与弧”的对应关系作为“圆心角、弧、弦”三者关系研究的突破口是自然的,符合学生的认知特点,能够直接引发学生的思考,同时帮助学生建立起探究的基本经验.教师追问“为什么要出现两个圆”,旨在促进学生对“同圆或等圆中”这个前提条件的深刻理解.
1.3 再探“圆心角、弧、弦” 的数量关系
问题如图3,连结AB,则AB就是∠AOB所对的弦,改变∠AOB的大小,AB的大小会改变吗?

图3
生1:AB的大小会改变,AB的大小随着∠AOB的变化而变化.
师:根据刚才的探究经验,你能提出什么问题?
生2:连结CD,若∠AOB=∠COD,则AB=CD.
师:如何验证你的发现呢?
生3:需要再画一个等圆,在等圆中作∠A′O′B′=∠AOB,然后把两个圆的圆心重合在一起,依据“圆的旋转不变性”,转动⊙O′,观察两条弦重合的情况.
生4:可以证明△AOB≌△COD.
师:验证后请总结你的发现.
生5:在同圆或等圆中,相等的圆心角所对的弦也相等.
生6:在同圆或等圆中,相等的圆心角所对的弧相等、所对的弦相等.
生7:∠AOB=∠COD,AB=CD.
师:请同学们自主探索并总结.

2 教学思考
2.1 从“思考”到“操作”,基于深度体悟的需要
体悟数学是基于数学核心素养的体悟学习,数学学习在本质上是体悟的过程,是促进学生元认知能力提升的过程.体悟数学教学主张学生通过体验、参与、在活动中切身体会,在实践中真实感受,使得数学思维在一次一次拔节中领悟和醒悟[2].本课的教学主要依据“圆的旋转不变性”,如何让学生深刻感受到这个性质非常重要.因此,在教学伊始,笔者设计了“思考与操作”活动,主要目的就是让学生深度体验并感悟这一特性.有些教师为了节省课堂教学时间,选择把“圆的旋转不变性”这个特点直接告诉学生或者在教学中一带而过,导致学生主体体验不足,从而影响了探究的效果.
2.2 从“一个圆”到“两个圆”,基于知识逻辑的需要
教学内容的设计要遵循知识的逻辑关系,知识形成过程的合理性决定了学生思维的有序性和深刻性.探索圆的对称性,究竟是从“一个圆”开始还是从“两个圆”开始,要搞清楚这个问题,首先要知道为什么要用两个圆.实际上用“两个圆”是为了解决“一个圆”中的问题.一些教师在处理这节课的内容时直接安排在“两个圆”中进行,导致在总结时学生不理解“在同圆或等圆中”这个前提条件,究其原因,还是混淆了二者之间的逻辑顺序.从“一个圆”到“两个圆”,反映的是知识的逻辑顺序,基于知识逻辑的教学,学生的理解是自然的、是深刻的.
2.3 从“一个要素”到“三个要素”,基于思维生长的需要
特级教师卜以楼指出:“要教给学生有生长力的数学,让学生在发现、发明、发展中生长数学.”他的教学主张为回归教学原点,反哺生命成长,彰显数学力量.在本节课的教学设计中,笔者尝试回归原点,引导学生从“一个要素”的研究开始探究,在探究中生长思维.首先由一个圆心角引导学生想到圆心角所对的弧,感受二者的对应关系.接着,改变圆心角的大小,感受圆心角所对应的弧也随之变化,进而帮助学生积累基本的活动经验.再引入一个相等的圆心角,会有怎样的发现呢?自然引发学生的猜想和验证.这一环节设计从“一个要素”出发,有效地引发学生发现“另一个要素”,从而提升了学生对同圆中的圆心角和所对应的弧的认识.一些教学设计中把“圆心角、弧、弦”三个要素放在一起探索,导致探究过程展开不充分、学生理解不透彻、学生思维无序等现象,关键原因在于没有关照学生思维生长的需要.从“一个要素”到“三个要素”,展现的正是学生数学生长的过程,让学习真正成为了学生成长的原动力,实现了学习的真正发生.
正如郑毓信教授所说,数学素养的真正核心是通过数学教学帮助学生学会思维,并能逐步学会想得更清晰、更深入、更全面、更合理.
